Q235B直缝焊管轴向冲击性能的理论和试验研究

郑玉卿, 朱西产, 董学勤, 马志雄, 2

(1.同济大学 汽车学院，上海 201804; 2.现代汽车零部件技术湖北省重点实验室, 武汉 430070)



Q235B直缝焊管轴向冲击性能的理论和试验研究

郑玉卿1, 朱西产1, 董学勤1, 马志雄1, 2

(1.同济大学 汽车学院，上海 201804; 2.现代汽车零部件技术湖北省重点实验室, 武汉 430070)

基于Alexander静态压溃模型和Cowper-Symonds 经验方程，推导出含应变率效应的圆管动态平均压溃力预测公式，同时论述了它与Abramowicz提出的理论公式异同点。然后利用跌落塔装置对9种规格的Q235B直缝薄壁焊管进行冲击试验，将理论预测值与实测值进行对比，结果表明：基于Alexander模型推导出的动态平均压溃力预测值整体偏小，而Abramowicz公式的预测值整体偏大。最后结合冲击试验过程和结果，修正了Abromowicz的平均压溃力预测公式，将应变率敏感系数3.91调为3.0，修正值与所有试验值吻合良好，最大偏差不超过8%；另外，还给出了用于预测中等尺寸薄壁焊管的简易动态峰值压溃力预测公式。

薄壁焊管；冲击试验；平均压溃力；峰值压溃力；理论预测

许多研究论文已论述了Q235B棒料或圆管的低周疲劳、不同速率的拉伸试验、侧向冲击等力学性能研究[1-4]，低碳钢薄壁圆管在轴向动态冲击载荷作用下的塑性屈曲现象和吸能特性也有论述[5]。Q235B直缝焊管作为低碳钢的一种，是目前市场上应用最为广泛且价格低廉的钢制品之一，供货状态多样，性能偏差较大，厚壁管主要用于中低压流体输送、建筑支撑结构，而薄壁管的良好塑性变形特性可用于开发车辆、船舶、飞行器的碰撞吸能结构[6]和公共安全碰撞防护装置如高速公路护栏柱、边坡防护结构等。

动态平均压溃力和峰值压溃力是表征Q235B等低碳钢薄壁圆管结构吸能水平的关键性能指标，它们直接涉及到被碰撞结构的平均加速度和峰值加速度水平，目前主要通过冲击试验测定或数值计算方法获得，因此若理论上能预测Q235B薄壁管在轴向冲击压溃过程中平的均压溃力和峰值压溃力，对于Q235B或类似低碳钢吸能结构设计开发是大有裨益的。

工程应用的碰撞吸能结构通常是在一定的冲击速度下吸收碰撞能量的，如汽车碰撞过程中，吸能结构应变率一般在1～120 s-1之间[7]，而本文所采用的跌落塔装置，其落锤的最高冲击速度为15 m/s，被冲击的吸能结构应变率基本涵盖了上述范围，与实际碰撞情形接近，是研究结构稳定吸能和耐撞性的重要手段之一。本文采用跌落塔冲击试验方法，结合材料的应变率效应，研究了Q235B直缝薄壁焊管在轴向冲击作用下的吸能特性水平，推导并修正了平均压溃力和峰值压溃力理论预测公式。

1 圆管动态吸能特性分析

基于Alexander提出的轴对称塑性静态压溃模型[8]和理论关系式，假定材料是理想刚塑性的，同时采用Cowper-Symonds模型考虑应变率的影响因素，研究图1的圆管轴对称轴向动态压缩过程的吸能特性。

图1 金属圆管轴对称动态压溃理论模型Fig.1 Theoretical axisymmetric dynamic crushing model for steel circular tube

1.1 静态平均压溃力

分析准静态压缩过程中形成一个完整褶皱的能量耗散过程[9]，假定褶皱是全部向外进行的，则塑性铰之间的管壁材料都会经历周向的拉伸应变，在单个褶皱形成过程中，出现三个圆形周向塑性铰，对圆管所做的外功由图1中的3条铰线的塑性弯曲以及塑性铰之间材料的周向拉伸所消耗。当一个褶皱完全被压扁时α=π/2，管壁塑性弯曲耗散的能量Wb为

2πM0(πD+2H)

(1)

式中:M0为单位长度塑性极限弯矩，M0=σsh2/4，N；其它未知量如图1标示。同时相应的管壁拉伸耗散能量Ws为

式中：σs为材料屈服应力。

根据能量平衡，外力功应等于塑性弯曲和塑性拉伸耗散的能量之和。

Pm2H=Wb+Ws

(3)

此处，Pm是完成整个褶皱变形过程的平均轴向力，将式(1)、(2)代入式(3)，可得

(4)

(5)

将式(5)代回式(4)，得到

(6)

上述分析过程是假定材料全部向外变形的，实际上圆管压溃过程是部分向内和部分向外变形的。假设全部向内变形，类似的分析可得

(7)

故假定圆管向内和向外变形的比例各占一半，取两者平均值可得

(8)

1.2 动态平均压溃力

Q235B属于软钢的一种，是典型的率敏感性材料。动态情况下惯性效应和应变率效应对于动态压溃力的影响都是值得关注的[10-11]。惯性效应主要受碰撞物之间的质量比和受冲击结构的“初始缺陷”强烈影响，它主要影响冲击过程的第一相，即轴向压缩的第一峰值载荷。ZHANG等[12]基于一个简单折板模型导出了冲击前后的能量比关系式，量化分析了第Ⅱ类的预先弯折板的惯性效应；而应变率效应属于材料的本身属性，它起到了增强材料屈服应力的作用，应变率越大，屈服应力增幅越大，持续影响动态冲击过程的材料力学属性。

根据Cowper-Symonds经验公式，可以将式(8)重新改写成动态平均压溃力预测式

(9)

(10)

式中：V0为碰撞体接触瞬间的初速度；t为一个完整褶皱动态压溃总时间。

将式(10)代入式(9)，可得动态平均压溃力公式

(11)

上述公式表达了软钢材质圆管在轴向动态冲击下的吸能影响因子和平均吸能水平。之后，ABRAMOWIZC等[13]基于Johnson提出的拉伸能量修正表达式、Wiezbicki静态压溃导出式和有效压溃长度理论，用拉伸极限应力σu替代屈服应力σs，分别给出了动态冲击载荷作用下，圆管在轴对称变形模式和非轴对称模式下的平均压溃力公式，其中低碳钢材料的应变率敏感系数B=6 844 s-1，q=3.91，由CAMPBELL等[14]低碳钢件中等应变率试验结果拟合获得，则式(11)改写为

和

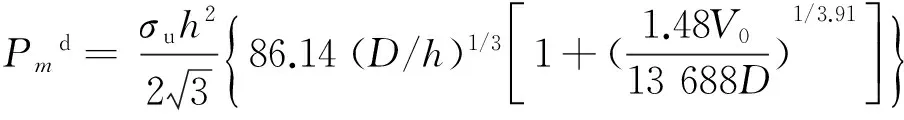
2 冲击吸能试验

2.1 冲击试验系统

图2所示为同济汽研自主开发的跌落塔冲击试验系统，该系统是将落锤(一个立体箱式框架，质量可调)提升至一定高度后释放，从而落锤产生对放置于基座上被测试结构的碰撞，其中基座中设有冲击过程的六自由度测力计，可准确获得试验过程的冲击力变化曲线，并在跌落塔侧面设有测速仪，可以获得落锤冲击时的初速度。落锤所获得的下落最大速度由落锤的总高度决定，跌落塔的四个拐角上铺设有垂直方向高精度导轨，采用滚珠轴承减少落锤与导轨间的摩擦，落锤的加速度为9.335 m/s2。本文采用它进行Q235B直缝薄壁焊管的轴向冲击吸能试验，落锤重量为1 380/695 kg。

图2 跌落塔冲击试验现场 图3 T5试件安装固定

Fig.2 Drop tower impact test site Fig.3 T5 test specimen installing and fixing

2.2 试件准备和固定

冲击试件所采用的Q235B直缝薄壁焊管均从上海钢材市场购得。截取合理长度，其一端采用焊接或则夹具夹持固定在一块带有四个M10螺栓孔的钢板上，钢板再与测力基座螺栓连接如图3的夹持固定方式，Ø76钢管系列均采用夹具夹持，而其余则采用图2中的焊接。

2.3 冲击试验记录和结果

9种规格Q235B直缝薄壁焊管冲击试验过程的详细试验记录和测试值列于表1，从表1可以看出，管壁越厚则动态平均压溃力越大，而管材外径对压溃力的影响较小。图4、5结果显示试件的轴向冲击塑性变形均是非轴对称变形模式，经观察其余规格焊管也一样。9种规格焊管试件尺寸均符合落在Andrews等基于大量铝管轴向压溃试验绘制的模式分类图[15]，而T9试件落在欧拉失稳变形区，但图6结果显然未发生欧拉失稳现象，这说明基于铝管试验结果的模式分类图可能对于率相关性的低碳钢薄壁圆管的变形预测存在较大偏差。冲击试验结束后，通过六分力测力计提取焊管的轴向冲击动态压溃力变化曲线，并采用Hyperworks软件自带的滤波器进行动态压溃力滤波处理，得到9种规格Q235B直缝薄壁焊管冲击过程的轴向压溃力变化历程曲线如图7所示。图7表明管壁厚度h是决定Q235B焊管轴向冲击过程平均压溃力和峰值压溃力的决定性因素，而管径D则是次要因素。管壁越厚，轴向压溃力越大，且峰值力也越大。其中，T8和T9焊管管壁较厚，压缩距离较短，所以冲击压溃力曲线(正三角和方块)总体较短，波动较大。

3 冲击试验结果讨论

3.1 动态平均压溃力

文献[1]在远离焊缝位置处采用线切割方式从Ø48×3.5的Q235B焊管上切下4根Q235B直缝焊管拉伸试件，并进行了单向拉伸试验，试验结果取均值可得Q235B焊管屈服强度σs=267 MPa，拉伸极限强度σu=356 MPa。表2列出了三种理论预测结果和试验结果对比，可见式(11)整体所预测的轴向动态冲击平均压溃力比Q235B直缝薄壁焊管的测试值偏小，随着管壁厚度增加，偏差也增大；式(12)预测值整体又偏大，但偏差分析显示其跟壁厚增加无关；而式(13)理论预测值则与本文试验结果偏差很大，故无法预测。经3种理论预测结果的均值和方差比较，可知式(12)预测直缝薄壁焊管的轴向冲击性能更加稳定。针对式(12)的理论预测值，同时也注意到两点：① T4预测值的偏差最大，偏差率达到23.21%，这可能由于管壁的测量误差或者管材内部缺陷所致，故忽略该样本；② 所有试件的平均压溃力预测值均比试验值大，这主要源于Abromowicz只采用了一个规格Ø58×1.2的低碳无缝管冲击试验拟合得到的，冲击速度是本文的2倍左右，故其式(12)中选用了较大的材料应变率敏感系数3.91所致。

图4 T2冲击试验结果 图5 T1、T7和T8冲击试验结果 图6 T9冲击试验结果

Fig.4 T2 impact test result Fig.5 T1, T7 and T8 impact test result Fig.6 T9 impact test result

表1 9种Q235B直缝薄壁焊管的冲击试验记录和测试结果

注：+是辅助验证试验，*号指冲击试验过程整根焊管全部被压溃。

表2 动态平均压溃力理论预测与试验结果对比

注：1*式(11)计算值，轴对称变形模式，T.X YU基于Alexander模型推导所得；2*式(12)计算值，轴对称变形模式，Abromowicz基于Johnson拉伸能量修正式推导所得；3*式(13)计算值，非轴对称变形模式，Abromowicz基于Wierzbicki静态压溃力表达式推导所得；4*式(14)计算值，其中T4预测值仅供参考。

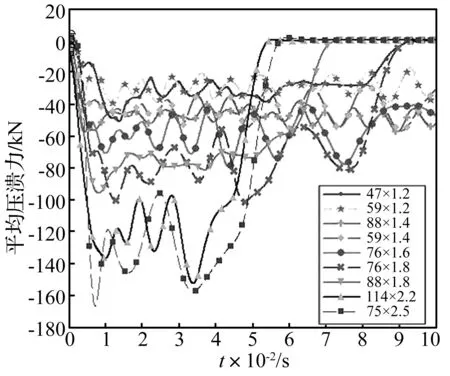
图7 9种Q235B直缝薄壁焊管的平均压溃力曲线对照Fig.7 Mean crushing force curve comparison for 9 kinds of Q235B thin-walled longitudinal welded tubes

结合上述两点和表2中冲击试验结果，可以选用式(12)来进行修正，考虑到本次试验的整体冲击速度较低，将应变率敏感系数从3.91调整为3，并把所有的修正预测值列于表2中，忽略T4数据影响，最大偏差是T6的7.94%，最小偏差是T9的0.1%。

(14)

3.2 动态压溃峰值力

通常峰值力主要出现在冲击过程的第一相中，即在初始碰撞体与焊管接触开始的弹性变形直到全截面塑性变形过程中，由于冲击试验过程有诱导变形坡口，坡口尺寸和位置存有差别，故峰值有时并非在第一个波峰上，受到材料应变率的影响，屈服强度会增大。假定焊管的材质属性一致，可得理想状态下的峰值力预测公式：

Pdp≈

(15)

表3列出了式(15)计算所得的T1～T9峰值力预测值与表1的试验峰值力进行对比，发现T1、T5、T6预测峰值与试验峰值较为一致，而其余规格的则偏差甚远；其次，所有的预测峰值力均远大于试验值，除了T6小于试验值。根据上述两点观察，可大胆做一个假设：假定T6试件中间存在一个Tcr临界试件，其规格尺寸代入式(15)得到的峰值力预测值与试验值完全相同。基于相同直径系列的T5、T6试验数据进行数值分析和函数插值拟合，得到预测峰值力和试验值完全相同时的Tcr试件厚度hcr=1.64 mm，直径Dcr=74.4 mm。

表3 动态压溃峰值力理论预测与试验结果对照

表3中T7的外径尺寸和壁厚均明显大于T5，但T7的试验峰值力仍略比T5的小，因此可得出结论：当截面相同的两根焊管时，直径大的动态压溃峰值力反而小；截面不同的两根焊管，外径尺寸增幅大于壁厚增幅的动态压溃峰值力反而更小；动态峰值压溃力的大小同样主要取决于壁厚。鉴于此，人为引入一个与直径、厚度相关的几何修正参数ξ来修正动态峰值力，则动态峰值力预测式(15)可改写为：

(16)

其中

(17)

式中:hi为Ti试件的实测厚度；Di为Ti试件的实测外径。

式(16)的峰值力修正值列于表3中与试验值对比，修正值大部分与试验值吻合度良好，但是T1、T2和T8的直径或壁厚与临界值尺寸均偏差较大，且其中一个接近或超过50%，因此预测偏差较大，故式(16)只能预测靠近临界值得中等尺寸焊管动态峰值压溃力。

4 结 论

(1) 基于Alexander轴向静态轴对称压溃模型和Cowper-Symonds应变率效应关系式，理论推导了金属圆管静动态的轴向压溃过程，得到了动态平均压溃力的预测公式，同时比较了它与Abromowicz提出的两个理论预测模型推导过程的异同点。Q235B直缝薄壁焊管动态冲击吸能试验结果表明：基于Alexander模型推导出的动态平均压溃力预测式(11)的预测值整体偏小，且偏差随厚度变化，而Abramowicz预测公式的预测值整体偏大，但偏差与厚度无关。

(2) 结合9种规格Q235B直缝薄壁焊管的动态冲击吸能试验条件和结果，对预测式(12)进行修正，提出了适用于Q235B直缝薄壁焊管动态平均压溃力预测的修正式(14)，其修正值与试验值之间的偏差最大不超过8%，理论上可以较好地预测Q235B直缝薄壁焊管的轴向动态冲击吸能特性。同时引入几何参数因子ξ，对冲击过程中焊管动态压溃的峰值力给出了简易预测式(16)，可用于预测中等尺寸直缝薄壁焊管的动态峰值力。

(3) Q235B直缝薄壁焊管轴向动态冲击特性的理论预测公式推导均建立在焊管周向材质均匀、强度一致的假设基础上，而焊管自身的残余应力、内部缺陷、焊接热影响等因素对平均压溃力和峰值力的影响仍有待进一步研究。

[1] 罗云蓉, 王清远, 刘永杰, 等. Q235、Q345 钢结构材料的低周疲劳性能[J]. 四川大学学报(工程科学版), 2012, 4(2): 169-175.

LUO Yunrong, WANG Qingyuan, LIU Yongjie, et al. Low cycle fatigue properties of steel structure materials Q235 and Q345[J]. Journal of Sichuan University(Engineering Science Edition), 2012, 4(2): 169-175.

[2] 曾力. 拉伸试验速率对低碳钢力学性能的影响[J]. 理化检验-物理分册, 2007, 43(1): 6-8.

ZENG Li. The influence of tensile test rate on mechanical property of low carbon steel[J]. PTCA (Part: A PH YS Test), 2014, 43(1): 6-8.

[3] 林莉, 支旭东, 范锋, 等. Q235B钢Johnson-Cook模型参数的确定[J]. 振动与冲击, 2014, 33(9): 153-158.

LIN Li, ZHI Xudong, FAN Feng, et al. Determination of parameters of Johnson-cook models of Q235B steel[J]. Journal of Vibration and Shock, 2014, 33(9): 153-158.

[4] 张荣. 圆钢管侧向冲击性能研究[D]. 黑龙江:哈尔滨工业大学, 2013.

[5] 顾红军, 赵国志, 陆廷金, 等. 轴向冲击下薄壁圆柱壳的屈曲行为的实验研究[J]. 振动与冲击, 2004, 23(4): 58-63.

GU Hongjun, ZHAO Guozhi, LU Tingjin, et al. Buckling of thin-wall cylindrical shell under axial impact[J]. Journal of Vibration and Shock, 2004, 23(4): 58-63.

[6] 余同希. 利用金属塑性变形原理的碰撞能量吸收装置[J]. 力学进展，1986，16(1): 1-12.

YU Tongxi. Impact energy absorbing devices based upon plastic deformation of metallic elements[J]. Advances in Mechanics, 1986, 16(1): 1-12.

[7] 王青春, 范子杰, 桂良进, 等. 泡沫铝填充帽型结构轴向冲击吸能特性的试验研究[J]. 机械工程学报，2006, 42(4): 101-106.

WANG Qingchun, FAN Zijie, GUI Liangjin, et al. Experimental studies on the axial crash behavior of aluminium foam-filled hat sections[J]. Chinese Journal of Mechanical Engineering, 2006, 42(4):101-106.

[8] ALEXANDER J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1960, 13(1):10-15.

[9] 余同希, [澳]卢国兴. 材料与结构的能量吸收[M]. 华云龙，译. 北京：化学工业出版社, 2006: 109-115.

[10] SU X Y, YU T X, REID S R. Inertia-sensitive impact energy-absorbing part Ⅰ: effect of inertia and elasticity [J]. International Journal of Impact Engineering, 1994, 16(4): 651-672.

[11] SU X Y, YU T X, REID S R. Inertia-sensitive impact energy-absorbing part Ⅱ: effect of strain rate [J]. International Journal of Impact Engineering, 1994, 16(4): 673-689.

[12] ZHANG T G, YU T X. A note on a‘velocity sensitive’ energy-absorbing structure[J]. International Journal of Impact Engineering, 1989, 8(1): 43-51.

[13] ABRAMOWICZ W, JONES N. Dynamic axial crushing of circular tubes[J]. International Journal of Impact Engineering, 1984, 2(3): 263-281.

[14] CAMPBELL J D, COOPER R H. Yield and flow of low-carbon steel at medium strain rates in proc conf on the physical basis of yield and fracture[C]// Inst of Physics and Physical Soc.London, 1966: 77-87.

[15] ANDREWS K R F, ENGLAND G L, GHANI E. Classification of the axial collapse of cylindrical tubes under quasi-static loading[J]. International Journal of Mechanical Sciences, 1983, 25(9): 687-696.

Theoretical and experimental studies on the axial impact behavior of Q235B longitudinally welded tubes

ZHENG Yuqing1, ZHU Xichan1, DONG Xueqin1, MA Zhixiong1,2

(1. School of Automotive Studies, Tongji University, Shanghai 201804, China;2. Hubei Province Key Laboratory of Modern Automotive Technology, Wuhan 430070, China)

Based on the Alexander’s theoretical crushing model and the empirical Cowper-Symonds equation, a formula including strain rate effect for predicting dynamic mean crushing force of circular tube was derived. And its derivation differences from the theoretical formulas put forward by Abramowicz were discussed. Then it adopted the drop tower rig to make the impact test for 9 kinds of Q235B longitudinally thin-walled welded tubes, and the test results were compared with theoretical prediction values. The result comparison shows that the predicting formula of dynamic mean crushing force derived from the Alexander’s model gives lower values, and Abramowicz’s formulas give higher values. At last, referring to impact test conditions and results, it modifies the Abramowicz’s formula by setting sensitivity coefficient of strain rate from 3.91 to 3.0. The modified values correlate well with all test results and the maximum deviation is lower than 8%. In addition, it also proposes a simple dynamic peak crushing force formula for predicting thin-walled welded tubes with media sizes theoretically.

thin-walled welded tube; impact test; mean crushing force; peak crushing force; theoretical prediction

国家高技术研究发展计划(863计划) (2012AA111302); 现代汽车零部件技术湖北省重点实验室开放基金课题(2013-05)

2015-08-03 修改稿收到日期：2015-09-15

郑玉卿 男，博士生，讲师，1983年2月生

朱西产 男，博士，教授，1962年6月生

O34

A

10.13465/j.cnki.jvs.2016.20.016