灰狼优化算法-投影寻踪模型在云南省水量分配中的应用

陈金红 程 刚

(云南省水利水电勘测设计研究院， 昆明 650021)



灰狼优化算法-投影寻踪模型在云南省水量分配中的应用

陈金红 程 刚

(云南省水利水电勘测设计研究院， 昆明 650021)

基于尊重现状和效率原则，选取水资源开发用率、总人口等11个指标构建云南省水量分配指标体系和水量分配投影寻踪(PP)模型．利用灰狼优化(GWO)算法搜寻PP模型最佳投影方向，构建GWO-PP水量分配模型对云南省16个州(市)水量进行分配．并通过4个典型测试函数对GWO算法进行仿真验证，仿真结果与文化算法(CA)、萤火虫算法(FA)和粒子群优化(PSO)算法进行对比．结果表明：GWO算法寻优效果优于CA、FA和PSO算法，具有收敛速度快、寻优精度高和全局寻优能力强等特点．GWO-PP模型水量分配结果较综合法水量分配结果更科学客观．模型及方法具有一定的可操作性和有效性，可为水量分配提供新的途径和方法．

水量分配； 指标体系； 灰狼算法； 投影寻踪

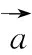
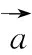
1 水量分配指标体系

水量分配属多目标多层次决策问题，涉及到流域或区域内社会、经济、水资源禀赋、水利设施供水能力等多方面因素，且又存在区域差异．在水量分配过程中，既要尊重现状用水水平、水资源开发利用等现状，又要兼顾用水效率．因此，结合云南实际，基于现状原则选取水资源开发用率、总人口、GDP、农业有效灌溉面积、完成水利投资、水利设施供水能力和用水量7个尊重现状分水指标；基于效率性原则选取农田灌溉亩均用水量、水库工程供水比重、万元工业增加值用水量和农田灌溉水利用系数4个效率性分水指标．利用此11个分水指标构建水量分配指标体系，见表1．

表1 水量分配指标体系

2 GWO-PP水量分配模型

2.1 投影寻踪模型

PP模型用于水量分配简要算法过程如下[5，12]：

1)数据预处理．设水量分配数据集为{x(i，j)|i=1，2，…，n；j=1，2，…，m}，为避免水量分配指标归一化后出现0的情形，对于正向指标采用下式进行数据处理．

(1)

式中，x(i，j)为第i个分水区域第j个分水指标值；xmax(j)、xmin(j)分别为第j个分水指标的最大、最小值；n、m分别为分水区域总数及分水指标数目．

(2)

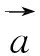
确定投影指标时，要求投影值z(i)的局部投影点尽可能密集，因此，构造投影指标函数为：

(3)

式中，Sz为投影值z(i)的标准差；Dz为投影值z(i)的局部密度．Sz、Dz表达式参见文献[5，13]．

3)优化投影指标函数．将搜寻最优投影方向问题转化为非线性最优求解问题，即

(4)

2.2 GWO算法

GWO算法通过构建α(第1层)、β(第2层)、δ(第3层)和ω(第4层)4层金字塔式的等级管理制度来实现算法模拟．其等级建立原则如下：

1)金字塔第1层为种群中的头狼，称为α，α为狼群中具有最高管理能力的个体，负责群体中捕食行为、食物分配等各项事务的决策．

2)金字塔第2层为β，它是α的智囊团队，协助α做出管理决策，当α出现空缺时，β将替补成为α．β对狼群中除α以外的其他成员具有支配权，同时起着反馈及协调的作用，它将α狼的命令下达给群体中的其他成员，并将监督执行情况反馈给α狼．

3)金字塔第3层为δ，δ听从α和β的指令，但可以支配ω层个体，负责侦察、放哨、捕猎等事务．较劣的α和β个体也将降为δ层个体．

4)金字塔最底层为ω，主要负责平衡种群内部关系以及照看幼狼等事务．

GWO算法中由α、β和δ执行追捕行为，ω跟随前三者进行猎物跟踪围捕，最终完成捕食任务．对于连续优化问题，假设GWO算法中灰狼种群数量为N，搜索空间为d维，其第i只灰狼在d维空间中的位置表示为xi=(xi1，xi2，…，xid)，种群中当前最优个体记为α，将适应度值排序为第二及第三的对应个体记为β和δ，剩余个体记为ω，猎物的位置对应于优化问题的全局最优解．

GWO算法实现步骤可简述如下[14-15]：

1)在捕食过程中，灰狼先对猎物进行包围，其灰狼个体与猎物之间的距离可用式(5)表示：

(5)

式中，Xp(t)表示第t代时猎物的空间位置；X(t)表示第t代时灰狼个体的空间位置；常数G为摆动因子，由式(6)决定．

(6)

式中，r1为[0，1]区间的随机数．

2)利用式(7)对灰狼空间位置进行更新：

(7)

式中，A为收敛因子，由式(8)决定：

(8)

式中，r2为[0，1]区间的随机数，a随着迭代次数增加从2线性递减至0．

3)定位猎物位置．当灰狼判断出猎物所处位置时，将由α狼带领β和δ对猎物进行追捕．在狼群中，α、β和δ狼最靠近猎物，可利用这三者的位置来判断猎物所处方位．α、β和δ狼跟踪猎物方位的数学描述可由式(9)～式(15)实现．

其中，先利用式(9)～式(14)计算群体内灰狼个体与α、β和δ狼之间的距离，然后利用式(15)判断出个体向猎物移动的方向．

(9)

(10)

(11)

(12)

(13)

(14)

(15)

2.3 GWO-PP水量分配实现步骤

GWO-PP模型水量分配实现步骤可归纳如下：

1)构建水量分配指标体系，利用式(1)进行指标一致性处理．

2)确定目标函数．由于GWO算法是求解极小值，因此将式(4)的倒数作为目标函数，即以式(16)作为适应度函数：

(16)

3)初始化算法参数．设置灰狼种群数量N、搜索空间为d维，最大迭代次数M，种群中当前最优个体记为α，将适应度值排序为第二及第三的对应个体记为β和δ，剩余个体记为ω．设定算法终止条件，令t=0，在解空间内随机初始化第i只灰狼在d维空间中的位置表示为xi(xi1，xi2，…，xid)．

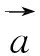
3 算法验证

选取4个典型测试函数见表2．对GWO算法进行仿真验证，求测试函数的极小值，并与CA、FA和PSO算法的寻优结果进行比较，见表3．

表2 基准函数

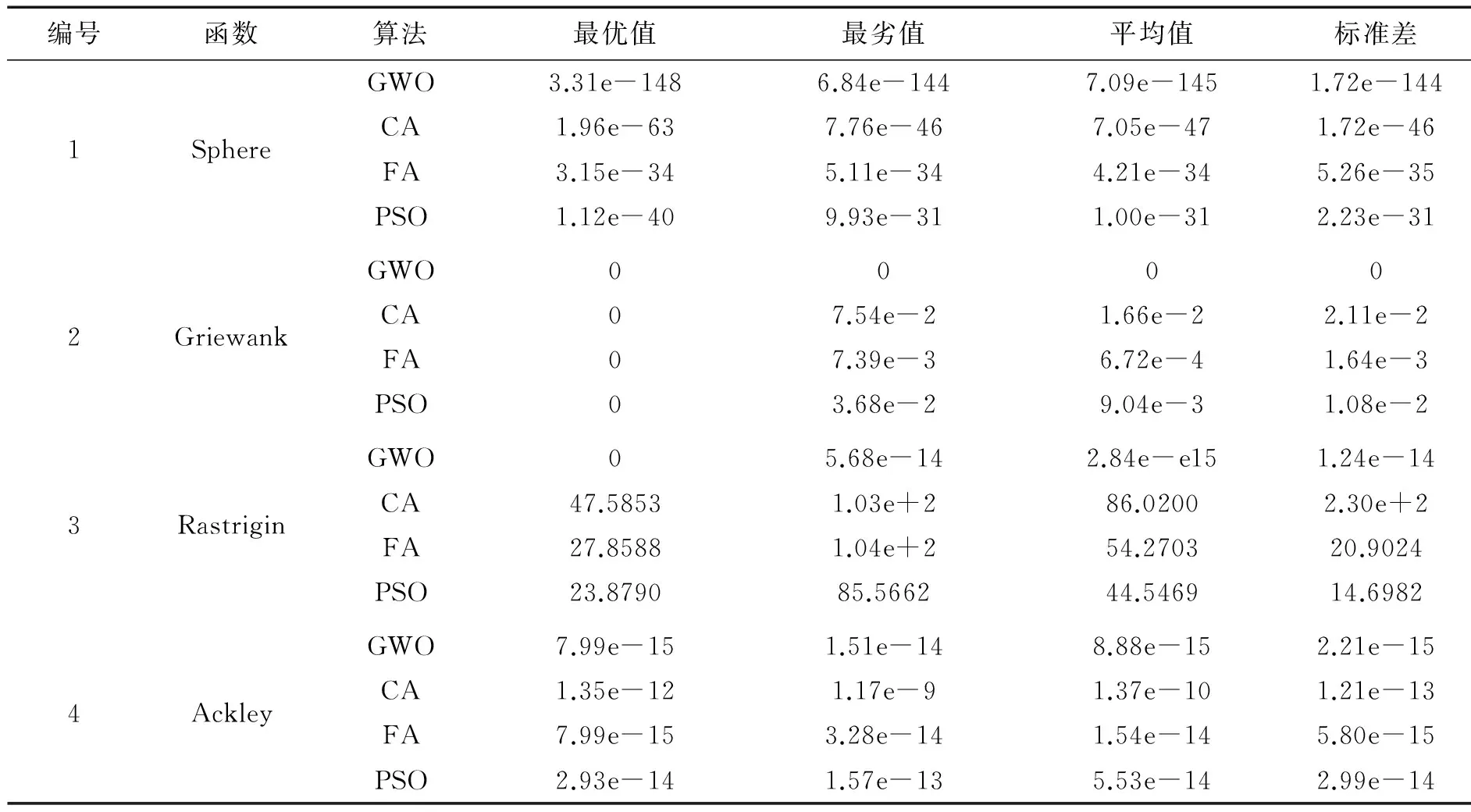
表3 函数优化对比结果

表2中，Sphere函数用于测试算法的收敛速度；Griewank函数用于测试算法对全局与局部搜索能力的平衡性能；Rastrigin函数用于测试算法的全局搜索能力；Ackley函数用于测试算法跳出局部极值的能力．每个测试函数均独立运行20次，分别求出最优值、最劣值、平均值和标准差4个方面对此4种算法进行评估．

实验参数设置如下：GWO算法最大迭代次数T=2 000，灰狼群体规模N=50．CA算法最大迭代次数T=2 000，群体规模m=50，根据标准知识产生的群体规模m′=50．FA算法最大迭代次数T=2 000，种群规模N=50，最大吸引度β0=2、光强吸收系数γ=1、步长因子α=0.2．PSO算法最大迭代次数T=2 000，种群规模N=50，ω=1，ω衰减系数=0.99，局部学习因子、全局学习因子c1=c2=2.0．

4种算法基于Matlab 2010a用M语言实现，对表2中4个测试函数重复进行20次寻优计算，并从最优值、最劣值、平均值、标准差4个方面进行评估．

1)从表3来看，对于Sphere函数，GWO算法寻优精度优于CA、FA和PSO算法(对比的各算法优化效果由优至劣，下同)至少90个数量级以上，表现出较快的收敛速度；对于Griewank函数，GWO算法寻优获得了理论最优值，寻优效果远远优于FA、PSO和CA算法，表现出较好的全局与局部搜索平衡能力；对于Rastrigin函数，GWO算法寻优效果优于PSO、FA和CA算法15个数量级以上，表现出较好的全局搜索能力；对于Ackley函数，GWO算法寻优精度同样优于FA、PSO和CA算法，具有跳出局部最优的良好性能．

2)综合比较而言，此4种算法的寻优能力由优至劣依次是GWO、FA、PSO和CA算法．

上述比较表明，GWO算法寻优效果优于CA、FA和PSO算法，具有收敛速度快、寻优精度高、全局寻优能力强以及收敛稳定性与收敛可靠性好等特点．

4 实例应用

4.1 研究区概况

云南省地处祖国西南边陲，位于北纬21°8′32″～29°15′8″和东经97°31′39″～106°11′47″之间，东与贵州、广西为邻，北同四川相连，西北隅紧倚西藏，西同缅甸接壤，南与老挝、越南毗连．辖昆明、曲靖、玉溪、保山、昭通、丽江、普洱、临沧、楚雄、红河、文山、西双版纳、大理、德宏、怒江和迪庆16个州市．境内河流分属长江、珠江、红河、澜沧江、怒江、伊洛瓦底江6大水系，多年平均水资源量2210亿m3．2013年国家分解并下达云南省2015年、2020年用水总量控制目标分别为184.87、214.63亿m3．同年云南省依据各州市2010～2012年水资源公报用水量均值、水利工程设计供水能力，并适当考虑各州市社会、经济发展潜力(暂称之综合法)完成所辖16个州市2015年、2020年用水总量控制目标的分解任务．2014年，云南省用水总量149.4亿m3，其中，农业、工业和生活用水量分别为103.3亿m3、24.6亿m3t和19.51亿m3，分别占用水总量的69.1%、16.5%和13.1%，农业用水仍是云南省第一用水大户．本文以2014年作为基准年对云南省所辖16个州市水量进行分配，各州市用水指标见表4．

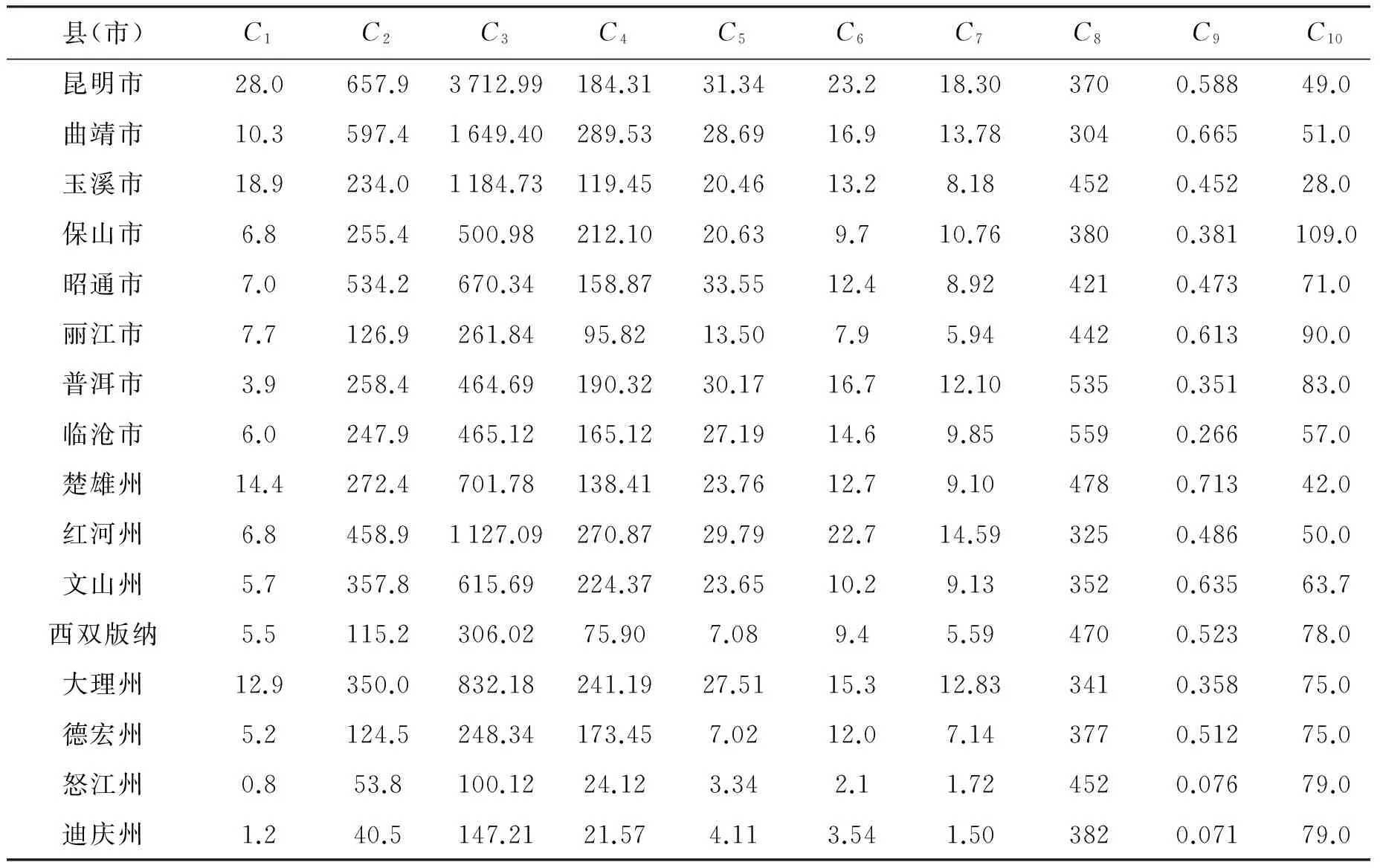
表4 云南省所辖行政区水量分配指标数据

4.2 水量分配模型求解

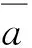
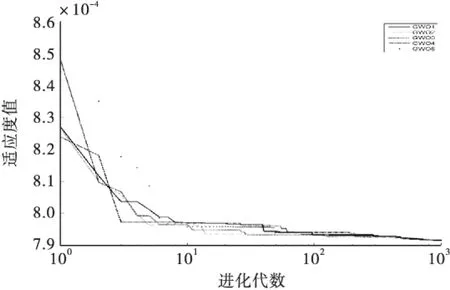
图1 GWO算法5次进化过程图

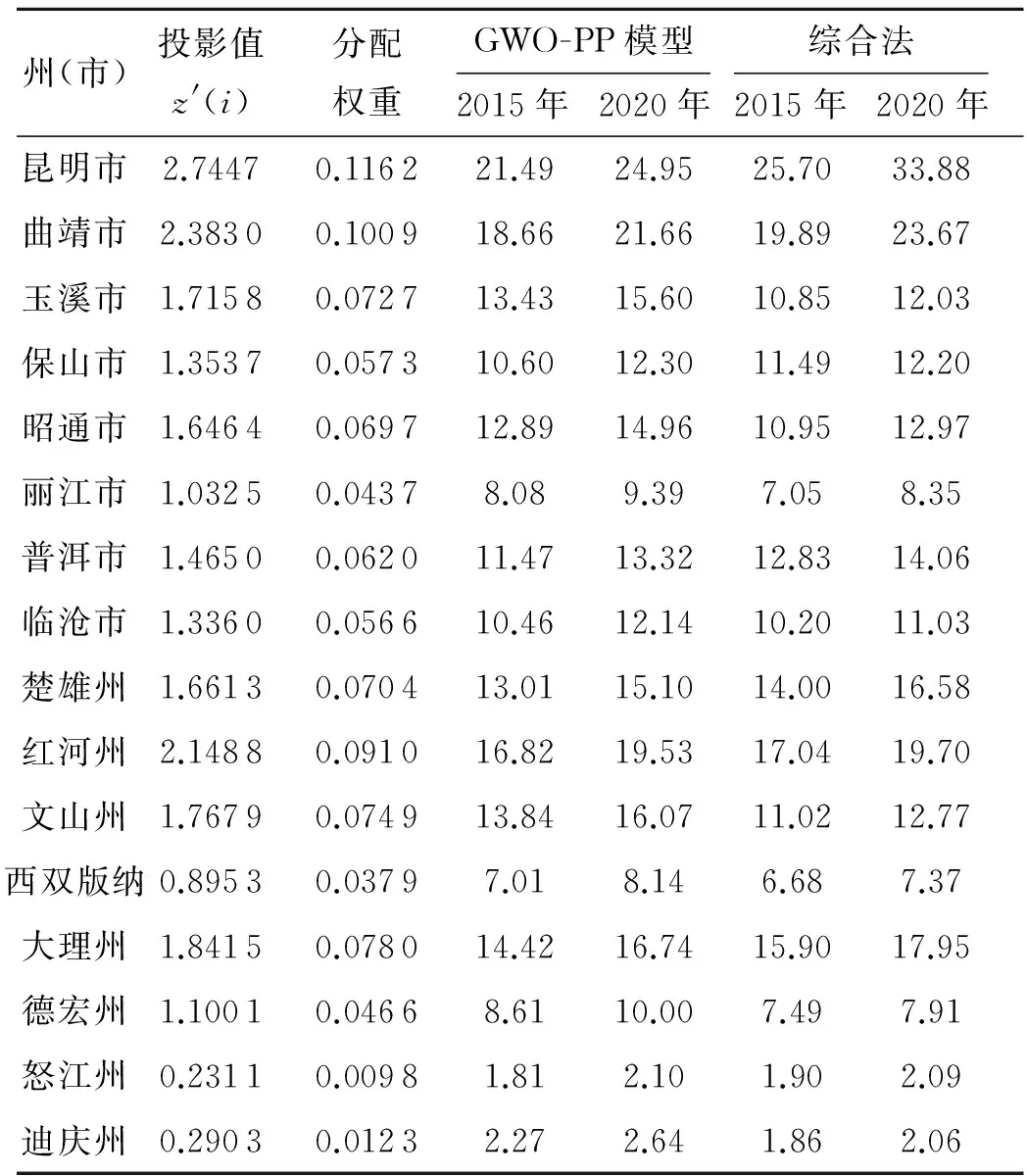
州(市)投影值z'(i)分配权重GWO-PP模型2015年2020年综合法2015年2020年昆明市2.74470.116221.4924.9525.7033.88曲靖市2.38300.100918.6621.6619.8923.67玉溪市1.71580.072713.4315.6010.8512.03保山市1.35370.057310.6012.3011.4912.20昭通市1.64640.069712.8914.9610.9512.97丽江市1.03250.04378.089.397.058.35普洱市1.46500.062011.4713.3212.8314.06临沧市1.33600.056610.4612.1410.2011.03楚雄州1.66130.070413.0115.1014.0016.58红河州2.14880.091016.8219.5317.0419.70文山州1.76790.074913.8416.0711.0212.77西双版纳0.89530.03797.018.146.687.37大理州1.84150.078014.4216.7415.9017.95德宏州1.10010.04668.6110.007.497.91怒江州0.23110.00981.812.101.902.09迪庆州0.29030.01232.272.641.862.06

从图1及表5可以得到以下结论：

1)从图1可以看出，GWO算法连续5次运行均获得了相对全局最优解7.915499×10-4，表现出较好的收敛精度和全局寻优能力．

2)从最佳投影方向优化结果来看，农田灌溉水利用系数、2014年完成水利投资、总人口指标权重最大，其对水量分配影响也最大；其次为2014年用水量和2014年水利设施供水能力指标；农田灌溉亩均用水量和万元工业增加值用水量指标权重最小，其对水量分配的影响也最小；其余4个指标权重在0.269 5～0.289 5之间，对水量分配的影响相对较小．

3)GWO-PP模型水量分配结果与综合法水量分配结果存在差异．从2015年水量分配结果来看，保山、临沧、楚雄、红河、西双版纳、怒江、迪庆两种方法的分配结果相差最小，在0.09～0.99亿m3之间；昆明、玉溪和文山两种方法的分配结果相差最大，分别为4.21、2.58和2.82亿m3；其余州市两种方法的分配结果在1.12～1.94亿m3之间．从2020年水量分配结果来看，保山、普洱、红河、西双版纳、怒江和迪庆两种方法的分配结果相差最小，在0.01～0.77亿m3之间；昆明、玉溪和文山两种方法的分配结果相差最大，分别为8.93、3.57和3.30亿m3；其余州市两种方法的分配结果在1.04～2.09亿m3之间．

4)从指标选取及各州市的经济、社会发展潜力来看，两种方法对部分州市水量分配结果差异较大的原因在于：①综合法仅考虑各州市2010～2012年水资源公报用水量、水利工程设计供水能力，并适当兼顾各州市社会、经济发展潜力，指标偏少；②由于云南省水资源监控能力建设滞后，各州市水资源公报用水量普遍采用定额法确定，与实际用水存在较大偏差；③综合法赖于社会、经济等指标的预测结果，由于预测结果往往偏离实际较大，因此造成水量分配结果存在较大差异．如表5中，采用综合法的昆明市水量分配结果明显偏大，尤其是2020年的水量分配结果为33.88亿m3，比GWO-PP模型的水量分配结果大8.93亿m3．

5 结 论

1)基于尊重现状和效率原则选取11个分水指标构建符合区域实际的水量分配指标体系，可为实行最严格水资源管理“三条红线”控制指标分解提供参考和借鉴．

2)通过4个典型测试函数对GWO算法进行仿真验证，并与CA、FA和PSO算法的寻优结果进行比较．表明GWO算法寻优效果优于CA、FA和PSO算法，具有收敛速度快、寻优精度高、全局寻优能力强以及收敛稳定性与收敛可靠性好等特点，具有较好的应用前景．

3)从实例水量分配结果来看，GWO-PP模型可以获得更加科学合理的水量分配结果．在实际应用中，可根据各区域实际增加或减少水量分配指标，以及通过时适调整指标数据，以获得更科学合理且满足各分水区域要求的水量分配结果．

[1] 孔琼菊，方国华．修河流域水量分配方案研究[J]．人民长江，2009，40(1)：27-30．

[2] 吕雁琴，李旭东．基于层次分析决策法的新疆阜康三工河流域水量分配研究[J]．生态经济，2011(9)：53-84．

[3] 程孟孟，陈进．多因子综合分析模型在赣江水量分配中的应用[J]．人民长江，2011，42(21)：50-52．

[4] 郭巧玲，黄 葵，杨琳洁．黑河干流中游水量分配研究[J]．人民黄河，2013，35(1)：36-38．

[5] 崔东文，郭 荣．SSO-PP模型在水源地安全保障达标评价中的应用[J]．水利经济，2015，33(5)：8-13．

[6] 王 柏，张忠学，李芳花，等．基于改进双链量子遗传算法的投影寻踪调亏灌溉综合评价[J]．农业工程学报，2012，28(2)：84-89．

[7] 王 婷，方国华，刘 羽，等．基于最严格水资源管理制度的初始水权分配研究[J]．长江流域资源与环境，2015，24(11)：1870-1875．

[8] 陈广洲，汪家权，解华明．粒子群算法在投影寻踪模型优化求解中的应用[J]．计算机仿真，2008，25(8)：159-161，165．

[9] 丁 红，刘 东，李 陶．基于改进人工鱼群算法的三江平原投影寻踪旱情评价模型[J]．农业工程学报，2010，26(12)：84-88．

[10] 赵建强，戴青松，陈必科，等．基于人工蜂群-投影寻踪法的南方某河水质综合评价研究[J]．节水灌溉，2014(8)：49-52．

[11] 王明昊，董增川，马红亮．基于混合蛙跳与投影寻踪模型的水资源系统脆弱性评价[J]．水电能源科学，2014(9)：31-35．

[12] 崔东文． 鸡群优化算法投影寻踪洪旱灾害评估模型[J]．水利水电科技进展，2015，36(2)：16-23．

[13] Mirjalili S，Mirjalili S M，Lewis A． Grey.Wolf Optimizer[J]．Advances in Engineering Software， 2014， 69 (7) ：46-61．

[14] 龙 文，赵东泉，徐松金．求解约束优化问题的改进灰狼优化算法[J]．计算机应用， 2015， 35(9)：2590-2595．

[15] 余 航，王 龙，文 俊，等．基于投影寻踪原理的云南旱灾评估[J]．中国农学通报，2012，28(8)：267-270．

[责任编辑 王迎春]

Application of Wolf Optimization Algorithm-Projection Pursuit Model to Water Allocation for Yunnan Province

Chen Jinhong Cheng Gang

(Yunnan Institute of Water & Hydropower Engineering Investigation, Design & Research, Kunming 650021, China)

Based on respect for the status quo and the principle of efficiency, water resources development with selecting rate, the total population of 11 indicators and other metrics to build Yunnan water allocation and water allocation system projection pursuit (PP) model. Utilization of gray optimization (GWO) algorithmic search PP model best projection direction, build GWO-PP water allocation model in Yunnan 16 states (cities) of water for distribution. And by four typical test function GWO algorithm simulation, the simulation results and Cultural algorithm (CA), firefly algorithm (FA) and particle swarm optimization(PSO) are compared. The results show that：GWO is better than CA, FA and PSO; it has good convergence speed, high precision and optimization of strong global optimization ability； GWO-PP water allocation results are more scientific and objective than ones of the integrated water allocaiton method. Models and methods have certain operability and effectiveness, so as to provide new ways and means for the water allocation.

water allocation； index system； gray wolf optimization algorithm； projection pursuit

10.13393/j.cnki.issn.1672-948X.2016.05.006

2016-05-03

国家水体污染控制与治理科技重大专项(201307102-006-01)；院士工作站建设专项(2015IC013)

陈金红(1982-)，男，工程师，主要从事水利、水资源规划、水利水电移民等工作．E-mail： cdwgr@163.com

TV212

A

1672-948X(2016)05-0029-07