含风电场的电力系统动态关键输电断面分析

罗钢，杨银国，钱峰

(广东电网有限责任公司电力调度控制中心，广东 广州 510600)



含风电场的电力系统动态关键输电断面分析

罗钢，杨银国，钱峰

(广东电网有限责任公司电力调度控制中心，广东 广州 510600)

大规模风电场接入高压输电网，将对电能传输与分配产生较大影响，有必要开展计及风电场出力特性的关键输电断面研究。通过将调度计划纳入到电网分析，引入风速和负荷预测误差的概率分布函数来描述系统中存在的不确定性因素，提出了一种基于概率潮流分析和复杂网络理论的电网分区及关键输电断面自动分析算法。该算法建立了动态关键输电断面分析模型以考虑电网调度运行的灵活性。在概率潮流分析的基础上，提出了计及不确定性因素的输电介数指标用于关键线路识别，进而基于电网小世界特性的分析，利用GN(Girvan Newman)算法将电网分割聚类，发现关键输电断面并对其重要性排序。通过含有风电场的CEPRI 36节点系统仿真计算，验证了本文模型、算法的有效性和实用性，并说明了含风电场电力系统的输电断面所具有的特点。

动态关键输电断面；风力发电；不确定性；输电介数；电网分区；复杂网络

随着传统化石类能源的消耗，国际社会对可持续发展和环境保护的要求日益提高，风力发电受到越来越多的重视。德国等发达国家对风电的利用已逐步由小规模陆地开发转向大规模海上开发[1]，经高电压等级远距离输送。我国风能资源丰富，但大多远离负荷中心，大规模、高集中开发和远距离、高电压输送已成为我国风力发电的发展方向。因此，越来越多的大型风电场接入高压输电网，相关研究受到更加广泛的重视。

近年来，电力系统大面积停电事故频繁发生。对这一系列事故的研究表明，简单故障引起功角失稳或电压失稳所引发的大停电事故已越来越少，连锁反应故障正逐步成为主要原因。运行在极限边缘的个别元件因低概率事件跳闸，极有可能引发相关输电断面连锁过载跳闸，最终导致系统崩溃。因此，从输电断面的角度分析电网，将有助于电网运行人员掌握电网脆弱环节及其当前运行状态进而实施调度控制策略，保证大电网的安全稳定运行。

传统的输电断面分析依赖于电网运行人员的长期工作经验，往往在地域划分的基础上离线获取。随着电网规模不断扩大、大型风电场接入，电网运行的随机因素大大增加，运行方式更加复杂多变，传统的输电断面分析方法不利于准确掌握电网真实的脆弱点，导致在线安全稳定分析的计算量大大增加。因此，有必要开展输电断面的自动分析研究。文献[2-3]从“割集”的角度给出了输电断面的定义及其自动发现方法，该算法对于关键断面的确定依赖于断面功率传输极限的计算，且求取所有割集的计算量较大，难于实时在线应用；文献[4-6]从输电断面有功安全性保护的角度，定义了由过载支路确定的一组潮流方向相同且与过载支路具有相同电源区或负荷区的并行输电断面为关键断面，基于网络图论进行搜索，该方法依赖于过载支路的选取且未考虑电网元件参数。此外，上述研究均未考虑电力系统不确定性因素对关键输电断面分析的影响。

复杂网络理论[7]已成为科学研究的重要领域，其核心研究内容是揭示复杂网络功能和结构之间的联系。社团结构[8]是复杂网络中的稠密联通分支，具有社团内连接紧密、社团间连接相对稀疏的特点。经验证国内外大部分电网均属于小世界网络[9-10]，即具有较大的聚类系数，且网络中的少数远程连接对电网输送电能和安全稳定运行起到关键作用。若利用复杂网络聚类方法发现社团间连接的关键线路，并对电网进行分割，将能够在电网分区的基础上进行关键输电断面的自动分析。

在上述背景下，本文分析了大规模风电场接入对输电断面的影响，提出了动态关键输电断面分析的概念，将调度计划纳入到电网分析中。然后，利用概率潮流分析方法引入风速预测误差、负荷预测误差，提出了计及不确定性因素的输电介数指标，将其应用到含大规模风电场的电力系统关键线路识别及关键输电断面分析中。最后，利用复杂网络理论构建了电网分区及关键输电断面自动搜索算法。CEPRI 36节点系统的算例验证了本文模型、算法的有效性和实用性。

1 大规模风电场接入对输电断面的影响

本文将有功潮流方向一致、线路之间开断灵敏度较大的电网割集定义为输电断面。其中对电网安全稳定运行具有重要影响，且能够完整地反映电网各主要电源集中区与负荷集中区间电能传输状态的断面定义为关键输电断面。关键输电断面集中反映了电网的脆弱环节及电能传输状态。

大规模风电场接入输电网对电能传输具有双重效应。一方面，风电接入可替代常规电源，提高电网可靠性，为运行人员提供更加灵活多变的运行方式，改善原有脆弱输电断面的运行状态，同时取得节能减排的环保效益。另一方面，风电的不确定性增加了输电断面的潜在运行风险，从而有可能抵消其对电网可靠性的贡献，极端情形下负面影响将导致某些输电断面由安全状态向临界状态转移，甚至出现系统崩溃。

在电网的调度运行中，必须综合考虑风电的灵活性与波动性，才能更好地发挥风电的环保效益，同时保证系统运行的可靠性。从输电断面自动分析的角度，若能够综合评估大规模风电场接入对网络电能传输及分配的双重影响，将有助于调度运行人员更好地权衡风电利用率与保证系统安全稳定运行之间的关系。

风电机组出力、负荷等不确定性因素存在明显的时间差异，仿照动态经济调度[11]的概念，本文将调度计划纳入到电网分析中，将其定义为动态关键输电断面分析，从而更好地考虑电能传输的灵活性与波动性。

2 考虑不确定性因素的概率风险模型

2.1 考虑不确定性因素的概率潮流模型

将系统的节点潮流方程S=h(x)与支路潮流方程Z=g(x)按照泰勒级数展开，忽略高次项可得

(1)

式中：S0、x0、Z0分别为节点注入功率、节点电压与支路潮流功率的期望值；ΔS、Δx、ΔZ为对应的随机扰动；J0为牛顿拉夫逊法最后一次迭代所用的雅克比矩阵；G0为支路潮流对节点电压幅值和相位的灵敏度矩阵。

由式(1)可知，若已知节点注入功率的期望值，节点状态变量与支路潮流的期望值可通过潮流方程直接求取，其大小取决于系统运行方式的安排。大规模风电场接入系统后，根据风速与负荷预测值制定调度计划，将其纳入到电网分析中，则能充分考虑灵活多变的运行方式。

下面进一步考虑电网的不确定性因素，由式(1)可推得

(2)

式中T0为支路潮流对节点注入功率的灵敏度矩阵。

由式(2)可知，支路潮流的随机扰动大小由两方面因素确定：a)节点注入功率自身随机扰动情况，即ΔS的波动大小；b)网络结构特征对节点注入功率扰动的传播情况，即灵敏度矩阵T0对ΔS的作用。

2.2 节点注入功率的不确定性模型

限于篇幅，本文仅讨论负荷与风电机组出力的不确定性模型。

通常采用均值为0、标准差为σL的正太分布来描述负荷预测误差随机变量ΔPL[11-12]。实际负荷随机变量的概率密度函数可描述为

(3)

式中ΔPL,re为实际负荷预测误差。

风电出力预测值同样存在偏差，利用风速预测和风-功曲线获取风电功率值具有较高精度[13]。文献[11，14-15]指出，风速预测误差Δv可以考虑一均值为0、标准差为σv的正态分布随机变量。这样，实际风速的概率密度函数与分布函数可分别描述为

(4)

式中：vre为实际风速；vp为风速预测值；v为实际风速随机变量，v=vp+Δv；Φ是标准正态随机变量的累积分布函数。

通过风电机组出力PW与风速间的分段函数关系PW=PW,p+ΔPW=T(v)[16]，可导出风电机组出力的概率密度函数为

(5)

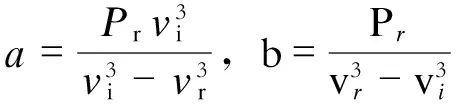
为了得到风电场的注入功率，需要考虑风电场内不同风机出力之间的相关性[17]。为了简化计算，本文假设各台风机参数完全一样，且风速完全相关。这样，风电场总注入功率为

(6)

式中：Pav为风电场注入有功功率；n为风机台数；PW为单台风机的功率。

2.3 支路潮流的波动功率模型

由式(2)可知，支路潮流波动功率随机变量ΔZ是节点注入功率预测误差的线性组合，求解对应的概率密度函数时需要利用随机变量的线性变换和卷积运算。不妨假设系统仅在节点i与节点j处分别有负荷与风电场接入电网，由式(2)可得

(7)

式中：T0,i和T0,j分别是矩阵T0在节点i和节点j处对应的值。

利用随机变量线性变换公式和卷积公式，可得ΔZ的概率密度函数表达式

(8)

式中ΔZre为实际支路潮流波动功率。

对式(8)求定积分可获取ΔZ的分布函数FΔZ(ΔZre)。由于fΔZ(ΔZre)与FΔZ(ΔZre)中的积分难于求得解析表达式，因此本文采用自适应辛普森数值积分计算方法近似求解。需要指出的是，若实际系统中包含的随机变量较多，卷积的计算量极大，此时可采用以半不变量为基础的Gram-Charlier级数法[18]近似求解ΔZ的概率分布。

利用ΔZ的概率分布函数，将给定置信概率α所对应的潮流波动量定义为线路潮流的波动功率ΔZf。进一步利用ΔZf构建计及系统潮流潜在运行风险的电网关键线路识别及关键输电断面分析方法。

2.4 计及不确定性的输电介数

社团结构研究中将某条边的介数用于衡量该边对社团间连通性的贡献和不属于任何社团的程度，其定义为经过该边的任意两点间最短路径的条数。目前，介数[19-20]已应用于电网连锁故障的分析，学者在此基础上进一步提出了加权介数[21]、电气介数[22]等概念分析电网的结构特征，识别关键元件。

本文结合电网传输电能的特点，定义了计及不确定性因素的线路输电介数指标

(9)

(10)

式中：G为发电机节点集合；D为负荷节点集合；L为输电线路集合；ail(l)为式(2)中灵敏度矩阵T0的对应元素；Cil为电网在发电机-负荷节点对(i,j)之间计及不确定性因素的传输容量；Z0(l)为当前运行方式下线路l传输的有功功率期望值；ΔZf(l)为给定置信概率下线路l的波动功率。

BTf的定义式(9)中，支路潮流对节点注入功率的灵敏度因子ail(l)反映了线路l对于发电机-负荷节点对(i,j)之间单位传输功率的贡献值，属于电网本身的结构属性。Cil可以理解为，仅从发电机节点i注入有功、负荷节点j吸收有功，当功率不断增加直到电网中第一条线路达到一定置信概率下的最大潮流，此时的注入有功功率即是Cil。Cil的定义式(10)中，Z0(l)是潮流分布的期望状态，能够反映运行方式的变化；ΔZf(l)则反映了支路潮流的波动情况。因此，BTf指标综合反映了电网结构特征、运行方式变化与不确定性因素对电网电能传输的影响，与介数、加权介数、电气介数等指标在关键线路识别中具有相似的特性，且更适合于关键输电断面的分析。

3 基于复杂网络理论的关键输电断面分析

3.1 电网分区算法

相关研究表明国内外大部分电力网络均属于小世界网络，即具有较大的聚类系数与较小的特征路径长度。部分高压输电线路的存在极大地缩短了电源集中区与负荷集中区的电气距离，这些长程连接发生故障时将会极大地降低电源区向负荷区的供电能力，致使电网的功能不能正常发挥，出现各区域内部的功率不平衡，最终导致电力系统稳定性的破坏甚至系统崩溃。

复杂网络聚类算法中，GN(Girvan Newman)算法是一种基于介数的社团发现算法，采用反复识别和删除社团间连接的策略聚类复杂网络，所采用的启发式规则为：社团间连接的边介数应大于社团内连接的边介数。GN算法最大的缺点是边介数计算量过大，计算效率低。

基于上述讨论，本文将电网中存在的少数长程连接作为构成关键输电断面的关键线路，利用第2.4节提出的BTf指标作为识别关键线路的依据，进而采用GN算法思想构造电网分区算法。基本步骤如图1所示。

图1 电网分区算法流程

电网分区算法完成后可以得到一个社团结构分解的树状图，即层次聚类树。将电网各分区间的联络线路集合称为分区断面。图2(a)所示为5分区电网的拓扑图，图2(b)为对应的层次聚类树。其中①至⑤为分区编号；1至5为分区断面编号，其大小表示了分区断面的开断顺序。

3.2 关键输电断面自动搜索

关键输电断面的搜索过程可描述为：发现电网中的分区断面→识别输电断面→剔除冗余输电断面→确定关键输电断面及其排序。

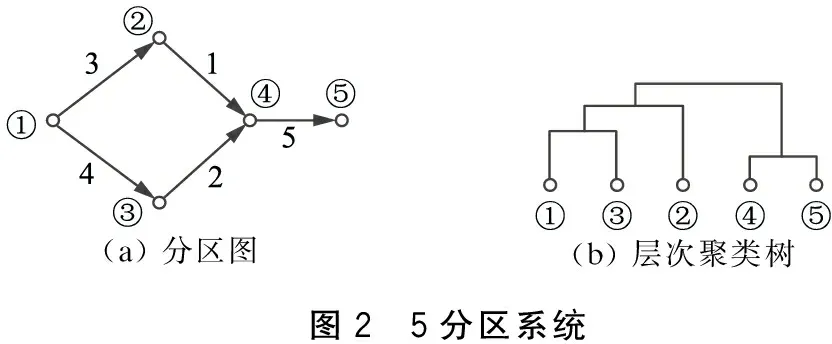
(a)分区图(b)层次聚类树图2 5分区系统

如图2(a)所示，分区断面可分为两类：即成环与不成环。对于不成环的分区断面可直接构成输电断面，如分区断面5；对于成环的分区断面，其潮流方向不成环，如分区断面1、2、3、4，此时分区断面的组合才能构成输电断面，图2(a)中可构成的输电断面为{1，2}、{2，3}、{3，4}、{1，4}。

事实上，每增加一个新的分区，将产生一个新的分区断面，同时原有分区断面可能被拆分。在图2(a)中，增加第一个分区时，1、2共同构成1个分区断面；增加第二个分区时，3是新产生的分区断面，而1、2被拆分为二。每一个新产生的分区断面若能组成多个输电断面，则彼此间互为冗余，选取其中开断次序最高的作为关键输电断面。即关键输电断面数与电网新增分区数相等。最后，按照所含有的分区断面最低开断次序将关键输电断面进行排序。图2(a)所示电网的关键输电断面及其排序为{1，2}、{2，3}、{1，4}、5。

4 算例仿真

采用中国电力科学研究院CEPRI 36节点系统进行仿真计算。系统接线如图3所示，通过合并变压器支路与小阻抗支路将网络简化后的系统共有17条输电线路，将B1处发电机设置为平衡机。在节点B33处接有额定容量为300 MW的风电场，风场内共有100台额定容量为3 MW的风力发电机。风速参数设置为：切入风速vi=4 m/s、额定风速vr=12.5 m/s、切出风速vo=20 m/s。研究3个时段，各个时段内负荷预测值不变，方差取预测值的10%。风电场中3个时段的风速预测值分别为8.5 m/s、10.5 m/s、13 m/s，风速预测误差的方差取预测值的10%。系统潮流风险槛值α设为0.98。

图3 CEPRI 36节点系统接线图

在典型运行方式下，采用第3章所提出的算法对算例系统进行关键输电断面分析，结果见表1，其中断面编号顺序即是典型运行方式下断面的重要性排序。

4.1 调度计划对关键输电断面分析的影响

在日常机组出力的调度计划安排中，需要根据风速预测值安排各机组的出力大小。在本文假设研究的3个时段内，节点B 7处的发电机出力根据风电场的注入功率期望值进行相应调整。

为了说明风电接入电网后，系统运行方式变化对关键输电断面分析结果的影响，首先进行未考虑风电机组出力与负荷功率不确定性的动态关键输电断面分析。分析结果中断面组成与表1完全相同，重要性排序见表2。

表1 典型运行方式下的关键输电断面

注：断面组成中各元素为2个节点间的线路。

表2 不同运行方式下的关键输电断面

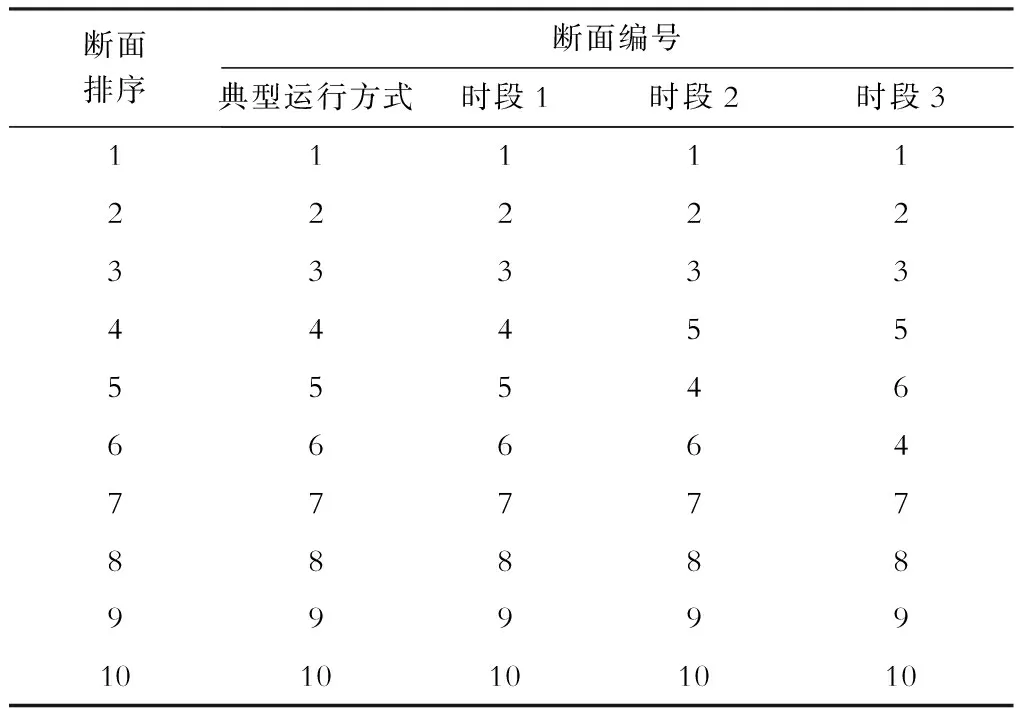
断面排序断面编号典型运行方式时段1时段2时段31111122222333334445555546666647777788888999991010101010

由表2可知，将调度计划纳入到关键输电断面分析中，将对分析结果产生一定的影响。其中，时段1风速较低，风机出力较小，系统运行方式变化不大，潮流分布的改变还不足以导致关键输电断面排序结果的变化。而时段2与时段3，随着风速加强，按照提前制定的调度计划，B34处的风机将增大注入功率同时减小B7处发电机出力，这将使该发电机的功率外送断面4所承担的潮流锐减，相应地其断面重要性程度也受到影响。在时段3中，断面4被B1处平衡机的功率外送断面5、6超越。

4.2 不确定性因素对关键输电断面分析的影响

将第4.1节中未考虑不确定性因素的情况记为场景1，进一步分析以下2种场景：

场景2，仅考虑风电机组出力的不确定性。

场景3，同时考虑风电机组出力与负荷功率的不确定性。

3种场景下所得到的关键输电断面组成与典型运行方式下的断面组成完全相同，仅在断面重要性排序中存在差异。时段1、时段3的排序结果如图4所示，图中N1为断面重要性排序号，N2为断面编号。

(a) 时段1

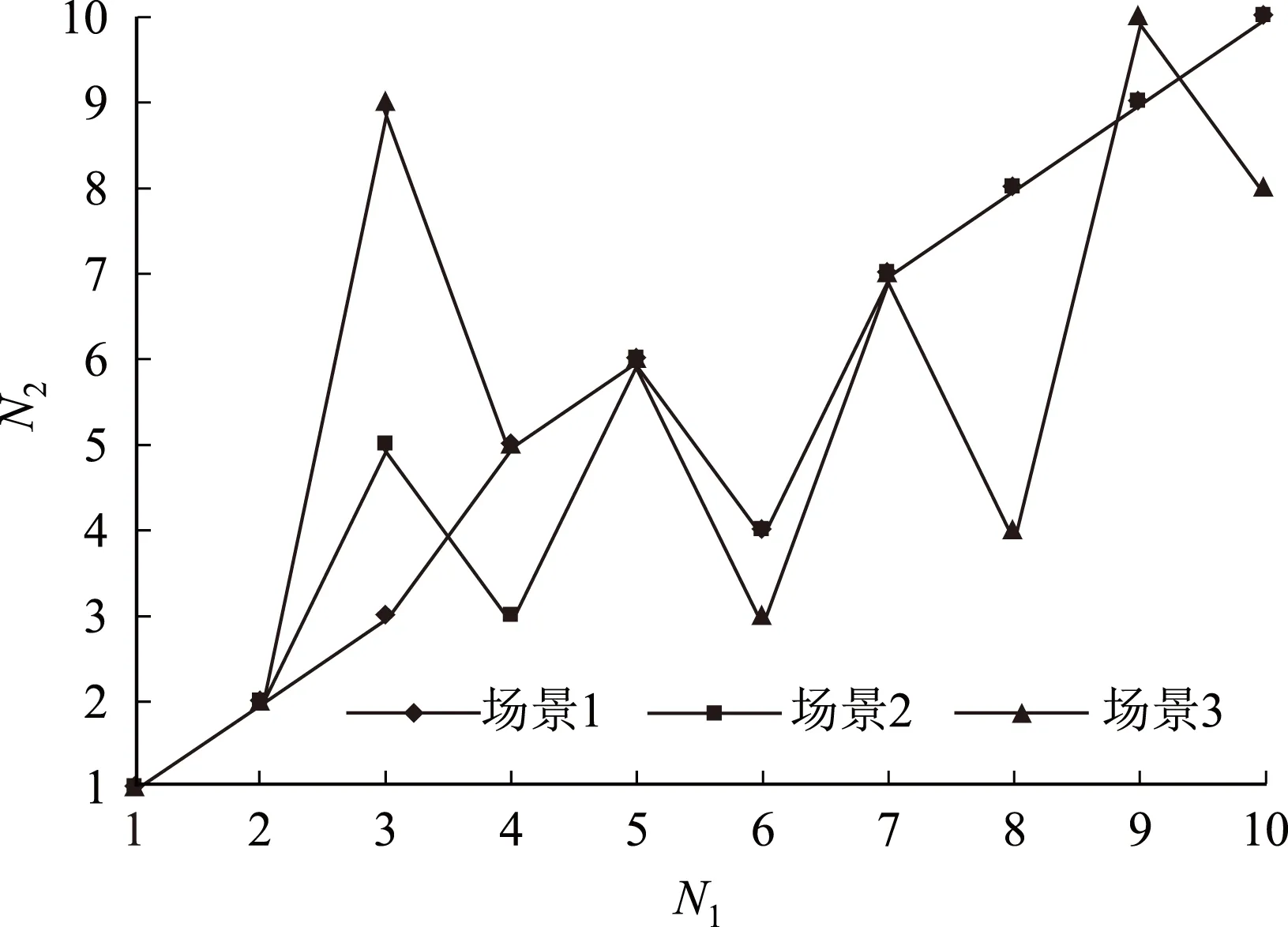
(b) 时段3图4 考虑不确定性的关键输电断面排序

图4中，对比场景1与场景2的排序结果可以发现，断面5的重要性在风电机组出力波动性的影响下得到了提升。通过对电网的分析可知，当风电场出现功率波动时，系统功率差额将由B1处的平衡机承担，对应的功率外送断面5的重要性也将随之增加。需要指出的是，实际系统在运行时，风电场波动功率可由所有发电机利用一次调频共同承担，或者按照调度计划进行分配，本文重点是分析风电功率不确定性对关键输电断面的影响，因此假设该功率由平衡机承担是合理的。

图4中，对比场景1与场景3的排序结果可以发现，在风电场与负荷功率波动的共同作用下，断面排序结果影响较大。其中对断面9的影响最大，时段1、时段3的排序分别从原来的第9位上升到第4与第3位。通过对电网的分析可知，该断面仅由1条输电线路组成，没有其它供电路径，且所分割的区域内负荷较重，从拓扑结构上分析该断面属于电网的脆弱环节。但在当前调度运行方式下B5处的发电机直接向B18的负荷供电，且二者刚好平衡，断面9的潮流为零，极大地降低了其重要性。然而，当考虑负荷波动性后，断面9将承担一定的波动功率，此时断面的脆弱性将被暴露出来，成为潜在的脆弱断面，其重要性程度也大大增加。

4.3 不确定性因素对输电介数的影响

为了进一步验证本文所提出的BTf指标在关键线路识别中对不确定性因素的考虑，计算时段1在3种不同场景下的BTf如图5所示。

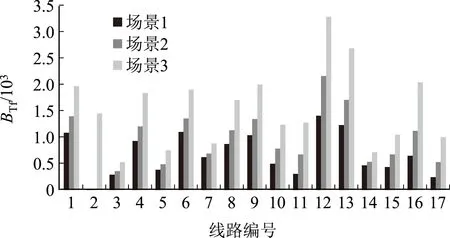
图5 不同场景下的输电介数对比

图5中，对比场景1与场景2的BTf可以发现，考虑波动功率后，各条线路的BTf均有不同程度的增加。其中，线路11与17(即线路B24-B23与B24-B9)的BTf增幅最大，均超过100%，它们共同组成断面5，表明该断面受风电功率不确定性的影响最大，其重要性排序也随之提高。与之相反，线路7与14(即线路B30-B19与B33-B34)的BTf增幅最小，均不超过15%，他们共同组成断面4，该断面的重要性排序随之降低。上述结论与波动功率由B1处发电机承担的事实相符。

图5中，对比场景2与场景3的BTf可以发现，考虑风电场与负荷的不确定性后，线路传输功率的波动性进一步加强。其中，线路2(即线路B16-B18)的BTf由0增加到1 460，其关键性程度迅速提高，所处断面9的重要性也由第9位上升到第4位，这与第4.2节中的分析结果完全一致。

综上所述，本文所提出的BTf指标与动态关键输电断面分析算法能够很好地考虑风电场接入对电网的影响，计及风机出力与负荷等多种不确定性因素，分析结果对调度运行人员具有较强的指导作用。

5 结论

大规模风电场接入输电网，将对电能传输与分配产生较大影响。本文从输电断面的角度分析了风电场为电网带来的灵活性与不确定性，提出了动态关键输电断面分析的方法，在其分析过程中引入概率潮流、复杂网络理论，构建了计及不确定性因素的电网分区及关键输电断面自动搜索算法，具有以下特点：

a)将调度计划纳入到关键输电断面分析中，能够充分考虑电网调度运行的灵活性。

b)所提出的计及不确定性因素的输电介数指标，能够反映电网结构与潮流分布共同决定的电网脆弱环节，通过控制线路波动功率的风险槛值，可有效识别受风电机组出力、用户负荷需求等随机因素影响的电网潜在脆弱环节。

c)电网分区与关键输电断面自动搜索算法对电网的分析结果具有较强的指导性，且计算速度快，适合应用于大电网。

[1] 张丽英，叶廷路，辛耀中，等．大规模风电接入电网的相关问题及措施[J].中国电机工程学报，2010，30(25)：1-9. ZHANG Liying，YE Tinglu，XIN Yaozhong，et al．Problems and Measures of Power Grid Accommodating Large Scale Wind Power [J].Proceedings of the CSEE，2010，30(25)：1-9.[2] 王成山，许晓菲，余贻鑫，等．基于割集功率空间上的静态电压稳定域局部可视化方法[J].中国电机工程学报，2004，24(9)：17-22.

WANG Chengshan，XU Xiaofei，YU Yixin，et al．Visualization of Power System Static Voltage Stability Region in Cut-set Space[J].Proceedings of the CSEE，2004，24(9)：17-22.

[3] 赵峰，孙宏斌，张伯明．基于电气分区的输电断面及其自动发现[J].电力系统自动化，2011，35(5)：42-46.

ZHAO Feng，SUN Hongbin，ZHANG Boming．Electrical Zone Division Based Automatic Discovery of Flowgates[J].Automation of Electric Power Systems，2011，35(5)：42-46.

[4] 周德才，张保会，姚峰，等．基于图论的输电断面快速搜索[J].中国电机工程学报，2006，26(12)：32-38.

ZHOU Decai，ZHANG Baohui，YAO Feng，et al．Fast Search for Transmission Section Based on Graph Theory[J].Proceedings of the CSEE，2006，26(12)：32-38.

[5] 程临燕，张保会，郝治国，等．基于线路功率组成的关键输电断面快速搜索[J].中国电机工程学报，2010，30(10)：50-56.

CHENG Linyan，ZHANG Baohui，HAO Zhiguo，et al．Fast Search for Key Transmission Section Based on Power Component of Line [J].Proceedings of the CSEE，2010，30(10)：50-56.

[6] 姚峰，张保会，周德才，等．输电断面有功安全性保护及其快速算法[J].中国电机工程学报，2006，26(13):31-36.

YAO Feng，ZHANG Baohui，ZHOU Decai，et al．Active Power Security Protection of Transmission Section and Its Fast Algorithm [J].Proceedings of the CSEE，2006，26(13):31-36.

[7] WATTS D J，STROGATZ S H．Collective Dynamics of ‘Small-world’ Networks[J].Nature，1998，393(6684)：440-442.

[8] GIRVAN M，NEWMAN M E J．Community Structure in Social and Biological Networks[J].Proceedings of the National Academy of Sciences of the United States of America，2002，99(12)：7821-7826.

[9] 孟仲伟，鲁宗相，宋靖雁．中美电网的小世界拓扑模型比较分析[J].电力系统自动化，2004，28(15): 21-24.

MENG Zhongwei，LU Zongxiang，SONG Jingyan．Comparison Analysis of the Small-world Topological Model of Chinese and American Power Grids[J].Automation of Electric Power Systems，2004，28(15): 21-24.

[10] 陈晓刚，孙可，曹一家．基于复杂网络理论的大电网结构脆弱性分析[J].电工技术学报，2007，22(10)：138-144.

CHEN Xiaogang，SUN Ke，CAO Yijia．Structural Vulnerability Analysis of Large Power Grid Based on Complex Network Theory[J].Transactions of China Electrotechnical Society，2007，22(10)：138-144.

[11] 周玮，孙辉，顾宏，等．计及风险备用约束的含风电场电力系统动态经济调度[J].中国电机工程学报，2012，32(1)： 47-55. ZHOU Wei，SUN Hui，GU Hong，et al．Dynamic Economic Dispatch of Wind Integrated Power Systems Based on Risk Reserve Constraints [J].Proceedings of the CSEE，2012，32(1)： 47-55.

[12] 李庚银，高亚静，周明．可用输电能力评估的序贯蒙特卡罗仿真法[J].中国电机工程学报，2008，28(25)：74-79.

LI Gengyin，GAO Yajing，ZHOU Ming．Sequential Monte Carlo Simulation Approach for Assessment of Available Transfer Capability [J].Proceedings of the CSEE，2008，28(25)：74-79.

[13] 杨秀媛，肖洋，陈树勇．风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25(11)：1-5.

YANG Xiuyuan，XIAO Yang，CHEN Shuyong．Wind Speed and Generated Power Forecasting in Wind Farm[J].Proceedings of the CSEE，2005，25(11)：1-5.

[14] LANGE M．On the Uncertainty of Wind Power Predictions—Analysis of the Forecast Accuracy and Statistical Distribution of Errors[J].Journal of Solar Energy Engineering，2005，127(2)：177-184.

[15] MATEVOSYAN J，SODER L．Minimization of Imbalance Cost Trading Wind Power on the Short-term Power Market[J].IEEE Transactions on Power Systems，2006，21(3)：1396-1404.

[16] ZHAO M，CHEN Z，BLAABJERG F．Probabilistic Capacity of a Grid Connected Wind Farm Based on Optimization Method[J].Renewable Energy，2006，31(13)：2171-2187.

[17] VILLANUEVA D，PAZOS J L，FEIJOO A．Probabilistic Load Flow Including Wind Power Generation[J].IEEE Transactions on Power Systems，2011，26(3)：1659-1667.

[18] 王成山，余旭阳．一种临界故障切除时间概率分布的求解方法[J].中国电机工程学报，2004，24(1)：6-10.

WANG Chengshan，YU Xuyang．A Method for Computing the Probability Distribution of Fault Critical Clearing Time[J].Proceedings of the CSEE，2004，24(1)：6-10.

[19] KINNEY R，CRUCITTI P，ALBERT R，et al．Modeling Cascading Failures in the North American Power Grid[J].The European Physical Journal B：Condensed Matter Physics，2005，46(1)：101-107.

[20] CRUCITTI P，LATORA V，MARCHIORI M．Model for Cascading Failures in Complex Networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics，2004，69(4)：266-289.

[21] 丁明，韩平平．加权拓扑模型下的小世界电网脆弱性评估[J].中国电机工程学报，2008，28(10)：20-25.

DING Ming，HAN Pingping．Vulnerability Assessment to Small-world Power Grid Based on Weighted Topological Model[J].Proceedings of the CSEE，2008，28(10)：20-25.

[22] 徐林，王秀丽，王锡凡．电气介数及其在电力系统关键线路识别中的应用[J].中国电机工程学报，2010，30(1)：33-39. XU Lin，WANG Xiuli，WANG Xifan．Electric Betweenness and Its Application in Vulnerable Line Identification in Power System[J].Proceedings of the CSEE，2010，30(1)：33-39.

(编辑 霍鹏)

Dynamic Key Power Transmission Sections of Power Systems Integrated with Wind Farms

LUO Gang, YANG Yinguo, QIAN Feng

(Electric Power Dispatch and Control Center of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510600, China)

Accessing of large-scale wind farms to high voltage power transmission grids will have greater effect on electric energy transmission and distribution, it is necessary to study key power transmission sections considering output characteristics of wind farms. By means of bringing dispatching plan into power grid analysis and introducing probability distribution functions of wind speed and load forecast errors to describe uncertain factors in the system, a kind of automatic analysis algorithm for power grid division and key power transmission sections based on probabilistic load flow (PLF) analysis and complex network theory is proposed to establish an analysis model for dynamic key power transmission sections for considering flexibility of power grid dispatching operation. On the basis of PLF analysis, power transmission betweenness considering uncertain factors is presented for line identification. And then, based on analysis for small world characteristics of power grids, Girvan Newman algorithm is used for power grid division clustering so as to find out key power transmission sections and sort their importance. Simulation calculation on CEPRI 36 node system integrated with wind farms verifies effectiveness and practicability of this model and algorithm as well as explains features of power transmission sections of power systems integrated with wind farms.

dynamic key power transmission section; wind power generation; uncertainty; power transmission betweenness; power grid division; complex network

2016-07-15

广东电网有限责任公司科技项目(K-GD2014-198)

10.3969/j.issn.1007-290X.2016.10.010

TM711

A

1007-290X(2016)10-0054-08

罗钢(1987)，男，四川广元人。工程师，工学博士，主要从事电力系统运行、分析与计算等方面的研究工作。

杨银国(1980)，男，湖北孝感人。教授级高级工程师，工学硕士，主要从事电力系统运行、分析与计算等方面的研究工作。

钱峰(1979)，男，湖南常德人。高级工程师，工学博士，主要从事电力系统运行、分析与计算等方面的研究工作。