峰值电流控制的H桥逆变器非线性现象的研究
韦许昌,陈志强,程淋伟,刘柿宏
(河海大学 能源与电气学院,江苏 南京 211100)
峰值电流控制的H桥逆变器非线性现象的研究
韦许昌,陈志强,程淋伟,刘柿宏
(河海大学 能源与电气学院,江苏 南京 211100)
以峰值电流控制的H桥逆变器为研究对象,分析了H桥逆变器电路的动力学特性。通过对H桥逆变器开关状态的描述,建立逆变器的离散时间模型,采用分岔图、折叠图、频闪映射分析了输入电压对系统性能的影响,运用Jacobian矩阵对H桥逆变器进行稳定性分析,最后通过仿真实验验证离散模型和理论分析的正确性。研究结果表明峰值电流控制的H桥逆变器存在非线性现象且受多个参数的影响,输入电压越高系统稳定域越大。
H桥逆变器;峰值电流控制;动力学;分岔;混沌
电力电子逆变器是现代电力工程的重要组成部分[1],属于非线性时变离散动力学系统,不合理的参数设置会产生各种类型的分叉和混沌等非线性现象,对逆变器的设计、开发产生极大的影响。近年来,人们开始利用非线性动力学理论研究逆变器的非线性行为,分析和揭示逆变器中的非线性现象及其产生的机理,这不仅有利于设计,也为在一定条件下利用这些固有的非线性现象来改善逆变器工作特性提供了理论基础[2],比如利用混沌扩频改善逆变器的电磁兼容和电磁干扰[3]等。因此,系统、全面地研究逆变器的动力学建模、分岔与稳定性,对逆变器有着理论物理意义和工程应用价值。
过去的20多年,人们对电力电子电路非线性现象的研究经历了从直流-直流(direct current-direct current,DC-DC)变换器到直流-交流(direct current-alternating current,DC-AC)变换器的转变,特别是近年来对逆变器混沌的研究取得了很大的突破。文献[4-5]最早研究了比例控制下H桥逆变器的分岔与混沌现象,为研究逆变器的非线性行为奠定了基础。文献[6]分析了比例控制下逆变器的分岔和混沌现象,并在文献[7]中引入快、慢2种尺度,建立了快慢离散模型,对其混沌行为进行更深入的研究。文献[8]分析了单极性正弦脉冲宽度调制(sinusoidal pulse width modulation,SPWM)下H桥逆变器的分岔和混沌现象。文献[9]提出了逆变器二阶模型线性化的方法,降低了系统稳定性分析的复杂度,简化了运算。文献[10]利用斜坡补偿对峰值电流控制的逆变器进行混沌控制,大大提高了逆变器的稳定性。
目前对逆变器非线性现象的研究基本上是采用三角波比较的SPWM控制方式,很少有对峰值电流控制的H桥逆变器非线性现象进行研究。在电力电子变换器中,电流控制技术包括峰值电流控制、平均电流控制和谷值电流控制,其中峰值电流控制是一种广泛应用的电流控制技术,其暂态闭环响应较快,且具有简单自动的磁通平衡功能和瞬时峰值电流限流功能。本文在前人的研究基础上,以峰值电流模式的H桥逆变器为例,通过建立离散时间模型,采用分岔图、折叠图、频闪映射和时域图等方法分析其分岔和混沌的非线性行为演化过程。
1 逆变器的原理和离散模型
H桥逆变器是一个典型的分段时变系统,随着开关管的不断导通与关断,其电路状态发生着变化,因此描述H桥逆变器的状态方程和离散模型也有着较大的变化。
H桥逆变器的原理如图1所示,主电路拓扑中E为直流输入电源,iL为流过负载的电流,电阻R和电感L构成负载,开关管S1—S4由绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)和二极管反并联组成。
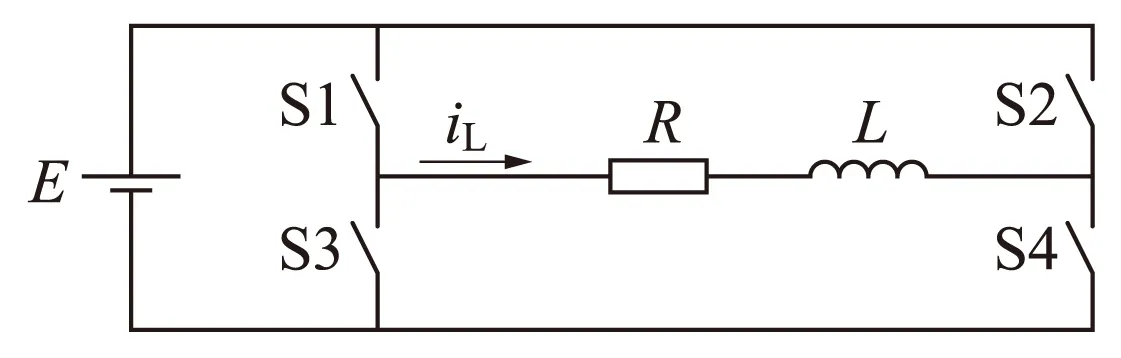
图1 H桥逆变器原理
主电路的工作状态有两种:
a)T1状态——S1、S4导通,S2、S3关断,其电流方程为
(1)
式中t为时间。
b)T2状态——S2、S3导通,S1、S4关断,其电流方程为
(2)
逆变器的控制电路由比较器、R-S触发器和时钟脉冲构成,如图2所示。当参考电流是直流量时,电路工作在直流斩波状态;当参考电流是交流量时,电路工作在逆变状态。在开始时刻,时钟脉冲来临,R-S触发器输出高电平使S1、S4导通,S2、S3关断,输出电流指数上升;当输出电流增至参考电流时,比较器复位触发器,R-S触发器输出低电平使S2、S3导通,S1、S4关断,输出电流指数下降,直到下一个时钟脉冲到来时,触发器再次输出高电平。
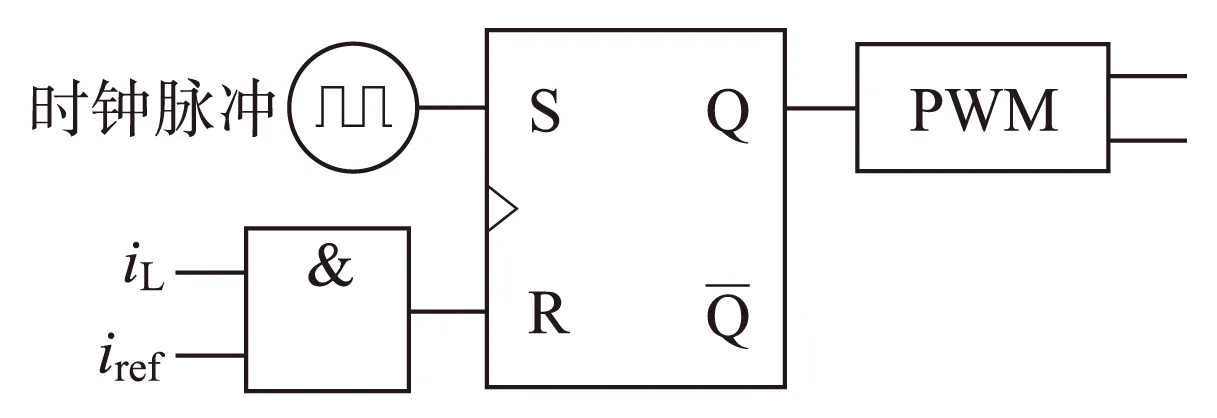
iref—参考电流;PWM—脉冲宽度调制,pulse width modulation的缩写。图2 峰值电流控制电路
设参考电流iref=Isin 2πft,其中I为参考电流的幅值,f为参考电流的频率,在每个开关周期开始时刻对电感电流进行采样,不同的开关状态对应的电感电流的时域波形如图3所示。当电感电流达到参考电流iref后,逆变器进入T2状态,对式(1)积分,求得第n个周期T1状态的占空比
(3)
其中
c=E/R.

T—开关周期,in—电感电流在第n个时钟脉冲周期开始时刻的采样值,in+1—电感电流在第n+1个时钟脉冲周期开始时刻的采样值,tn—在第n个时钟脉冲周期内T1状态持续的时间,tn+1—在第n+1个时钟脉冲周期内T1状态持续的时间。图3 电感电流波形
综上所述,可得到峰值电流控制的H桥逆变电路参数在区间变化时的离散时间模型。在2个相邻的时钟周期nT和(n+1)T内,逆变器的离散时间映射模型为:

其中
β=RT/L.
2 逆变器的动力学分析
2.1 输入电压的分岔分析
以输入电压E为分析参数,研究峰值电流控制的H桥逆变器在输入电压变化时所体现的丰富的动力学行为,基于离散时间模型可以得到峰值电流控制的H桥逆变器输入电压变化时的分岔图、频闪图和折叠图。系统仿真参数:负载电阻10 Ω,负载电感0.02 H,直流电压15~50 V,开关周期0.1 ms,参考电流幅值1 A。
根据系统离散迭代模型,以固定采样间隔(一般选开关周期)对迭代稳定后的状态变量进行采样并保留采样点的值,可得到系统的频闪采样图,如图4所示。

图4 输入电压频闪图
通过改变直流输入电压,可以观察到H桥逆变器中存在的非线性现象。当E=25 V时,在每个周期的[π/2,3π/2]区域内,图形对应着杂乱的采样点,表明系统处于混沌态;当E=45 V时,系统的采样点形成一条单值线,系统处于单周期稳态。
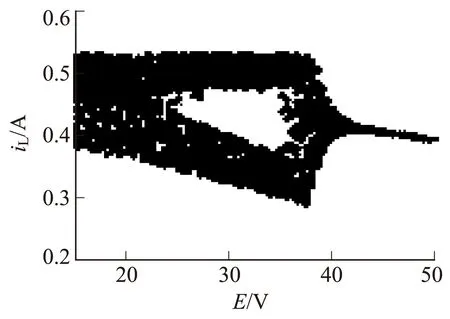
图5 输入电压分岔图
根据频闪采样图,利用矩阵实验室(Matrix Laboratory,MATLAB)软件编程,对每个周期的[π/2,3π/2]区域进行采样,可得到iL随输入电压E变化的分岔图,仿真结果如图5所示。从图5可以看出:随着输入电压的增大,系统表现为从混沌运动状态突然跃变为单周期运动状态,这与边界碰撞分岔的表现形式正好相反,当输入电压达到45 V后系统激变进入稳定状态。
为了进一步分析直流输入电压E所产生的非线性现象,采用折叠图作进一步说明。折叠图可以直观地判断系统出现的分岔和混沌现象,它避免了雅可比矩阵方法计算繁琐并依赖平衡点的缺点。选取任意初值带入系统离散方程进行迭代,将稳定后的状态变量的数个周期时刻对齐后折叠,得到一个周期的波形即为系统的折叠图,它能形象地反映系统的运行状态。
图6是不同输入电压下的折叠图。由图6可知:当E=25 V时,部分采样点形成2条正弦线,说明系统处于2倍分岔状态,部分采样点密集填充了大部分区域,说明系统处于混沌状态,也表明在每个周期不同时刻系统所处的状态不同,可以说在一个周期不同的点采样形成的分岔图也不一样;当E=45 V时,各个正弦波的每个采点都完全重合,形成一条光滑的正弦曲线,此时逆变器工作于稳定的周期状态。
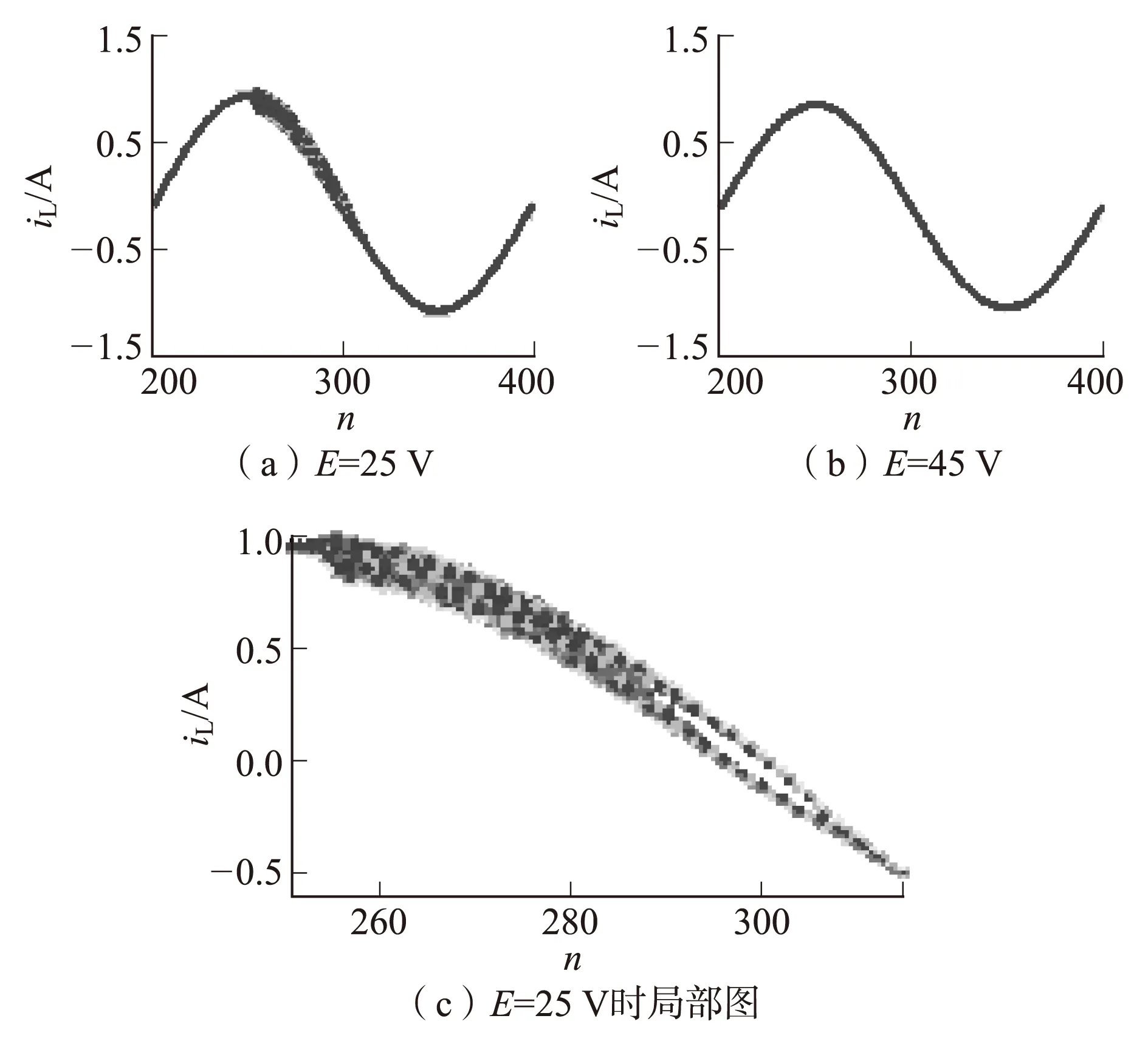
图6 输入电压折叠图
图4至图6直观地反映了不同的输入电压下系统动力学演化过程,对于峰值电流控制的H桥逆变器,在其他参数不变的情况下,随着输入电压的增加,逆变器的工作状态将由混沌状态转变为稳定状态。
2.2 不同的输入电压对系统性能的影响
以输入电压E作为可变量,运用iL的时域图、电感L分岔图(如图7所示)、负载电阻R分岔图(如图8所示)说明不同的输入电压等级对系统稳定域的影响。

图7 不同输入电压的电感分岔图

图8 不同输入电压的电阻分岔图
对比图7、图8发现:不同的输入电压所对应的R和L分岔图的稳定域不同,输入电压越高稳定域越大;E=25 V时系统早早地由单一的稳定状态进入混沌状态,E=45V时电感的分岔图始终处于稳定状态,电阻分岔图的稳定区间也明显增大,这与图5的输入电压的分岔图走势正好吻合。
3 电路稳定性分析
根据式(4)所述的离散模型,利用Jacobian矩阵对系统进行稳定性分析,Jacobian矩阵稳定性分析是研究系统运行的常用方法。离散系统第n+1次迭代值Xn+1=f(Xn,Dn),其中Xn为离散系统第n次迭代值,Jacobian矩阵的第n个元素
(5)
式中XQ、DQ为系统的单周期稳定解,其值可以通过迭代的方法利用XQ=f(XQ,DQ)求得。
对于峰值电流控制的H桥逆变器而言,每个开关周期内参考电流都在发生变化,把参考电流设定为控制参数,在一个开关周期内可以认为是一个恒定值[11],即in+1=f(in,iref),稳定点为in+1=in,通过Jacobian矩阵的定理,得到判断系统的稳定条件为


由此可得系统的平衡点
代入数据可得到系统的稳定条件为
当以输入电压E为分岔点时,令λmax=-1,E=45 V,可得iref=0.113 A;保持参考电流不变,改变E=25 V,可得λmax=-1.04,系统不稳定。
稳定性分析结果与仿真结论完全一致,从理论上解释了H桥逆变器发生分岔的原因。
4 仿真验证
为了验证上述分析的有效性,本文基于MATLAB电路仿真平台进行仿真验证,仿真参数与2.1节相同,得到的时域波形如图9所示。

图9 时域波形图
从图9不难看出,仿真结果与上述理论分析结果一致,表明建立的电流控制变换器离散时间模型是可行的。当E=25 V时,电感电流出现振荡和波纹,随着输入电压E的增加,振荡和波纹消失,逆变器从不稳定到稳定。
5 结论
本文以峰值电流控制的H桥逆变器为例,系统地研究了H桥逆变器的动力学理论,包括动力学离散时间模型建立、混沌分岔分析、稳定性分析。研究结果表明:峰值电流控制的H桥逆变器属于典型的非线性系统,其工作状态受多个参数的影响,且输入电压越高系统稳定域的范围越大,实际应用中应合理选择参数。
[1] AVRUTIN V, MOSEKILDE E, ZHUSUBALIYEV Z T, et al. Onset of Chaos in a Single-phase Power Electronic Inverter[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2015, 25(4): 043114.
[2] TSE C K, BERNARDO M D. Complex Behavior in Switching Power Converters[J]. Proceedings of the IEEE , 2002, 90(5):768-781.
[3] GIRAL R, EI A A, MARTINEZ S L, et al. Current Control Technique for Improving EMC in Power Converters[J]. Electronics Letters, 2001,37(5);274-275.
[4] ROBERT B, ROBERT C. Border Collision Bifurcations in a One-Dimensional Piecewise Smooth Map for a PWM Current-programmed H-bridge Inverter[J]. International Journal of Control, 2002, 75(16/17): 1356-1367.
[5] IU H H C,ROBERT B. Control of Chaos in a PWM Current Mode H-bridge Inverter Using Time-delayed Feedback[J].IEEE Transactions on Circuits and Systems,2003,50(8):1125-1129.
[6] 王学梅,张波. 单相SPWM逆变器的分岔及混沌现象分析[J]. 电工技术学报,2009,24(1):101-107.
WANG Xuemei,ZHANG Bo. Study of Bifurcation and Chaos in Single-phase SPWM Inverter[J].Transactions of China Electrotechnical Society,2009,24(1):101-107.
[7] 王学梅,张波,丘东元.H桥正弦逆变器的快变和慢变稳定性及混沌行为研究[J].物理学报,2009,58(4):2248-2254.
WANG Xuemei,ZHANG Bo,QIU Dongyuan. The Fast-and Slow-scale Stabilities and Chaotic Motion of H-bridge Sine Inverter[J]. Acta Physica Sinica,2009,58(4):2248-2254.
[8] 刘洪臣,杨爽.单相H桥逆变器单极性正弦脉宽调制下的分岔及混沌行为研究[J].物理学报,2013,62(21):44-50.
LIU Hongchen,YANG Shuang. Study on Bifurcation and Chaos in Single-phase H-bridge Inverter Modulated by Unipolar Sinusoidal Pulse Width Modulation[J]. Acta Physica Sinica,2013,62(21):44-50.
[9] 周林,龙崦平,郭珂,等.基于系数线性化模型的逆变器分岔与混沌现象研究[J].电力自动化设备,2013,33(7):100-104.
ZHOU Lin,LONG Yanping,GUO Ke,et al. Bifurcation and Chaos of Inverter System Based on Coefficient Linear Model[J]. Electric Power Automation Equipment,2013,33(7):100-104.
[10] 胡乃红,周宇飞,陈军宁. 单相SPWM逆变器快标分叉控制及其稳定性分析[J].物理学报,2012,61(13):50-57.
HU Naihong,ZHOU Yufei,CHEN Junning. Control of Fast-scale Bifurcation in Single-phase SPWM Inverter and Its Stability Analysis[J]. Acta Physica Sinica,2012,61(13):50-57.
[11] 龙崦平. 单相全桥逆变器分岔与混沌现象研究[D]. 重庆:重庆大学, 2013.
(编辑 李丽娟)
Nonlinear Phenomena in H-bridge Inverter by Peak-current Control
WEI Xuchang, CHEN Zhiqiang, CHENG Linwei, LIU Shihong
(College of Power and Electrical Engineering, Hohai University, Nanjing, Jiangsu 211100, China)
Taking the H-bridge inverter by peak-current control for a research object, this paper analyzes dynamic characteristics of H-bridge inverter circuits. It describes switch states of the H-bridge inverter and establishes a discrete time model for the inverter. By adopting bifurcation diagram, folded diagram and stroboscopic map, it analyzes influence of input voltage on the system. Jacobian matrix is used for stability analysis on the H-bridge inverter and finally simulating experiments are conducted for verifying validity of the discrete model and theoretical analysis. Research results indicate that there exists nonlinear phenomena in the H-bridge inverter by peak-current control which is affected by several parameters, and the higher the input voltage is, the larger the system stability domain is.
H-bridge inverter; peak-current control; dynamics; bifurcation; chaos
2016-05-23
10.3969/j.issn.1007-290X.2016.10.007
TM464
A
1007-290X(2016)10-0037-05
韦许昌(1990),男,江苏淮安人。在读硕士研究生,主要研究方向为新能源变换器非线性现象。
陈志强(1991),男,江苏淮安人。在读硕士研究生,主要研究方向为风电系统的谐波抑制。
程淋伟(1992),男,江苏南通人。在读硕士研究生,主要研究方向为风光储协调控制运行。

