电动汽车与可再生能源的协调优化
周杨,王东华
(1. 广东电网发展研究院有限责任公司,广东 广州 510080;2.中国南方电网有限责任公司超高压输电公司广州局,广东 广州510405)
电动汽车与可再生能源的协调优化
周杨1,王东华2
(1. 广东电网发展研究院有限责任公司,广东 广州 510080;2.中国南方电网有限责任公司超高压输电公司广州局,广东 广州510405)
针对电动汽车和可再生能源之间的多目标协调调度,建立了以配电网负荷波动最小、总网络损耗最小和电动汽车用户充电成本最小为目标函数的多目标协调控制模型,并采用量子粒子群多目标搜索算法进行求解,得到各个时刻电动汽车合理的入网数量。以IEEE-33节点配电系统进行仿真实验,结果表明,利用电动汽车的电池储能系统作为电网和可再生能源的缓冲,能降低可再生能源发电间歇性和电动汽车入网随机性对电网的影响,促使电网侧和用户侧的双边利益最大化。
电动汽车;可再生能源;协调控制;量子粒子群优化算法;多目标优化
随着环境污染和化石燃料枯竭等问题的日益凸显,电动汽车被认为是减少对化石能源依赖和二氧化碳排放的有效解决方法,正受到各国政府和相关企业的高度关注[1-3]。电动汽车数量增长,其入网充电势必会给现有电网造成巨大的冲击。太阳能、风能等可再生能源的输出功率具有波动性,直接接入电网会对电网的电能质量和稳定性产生较大的影响。电动汽车电池是潜在的储能电源,善加利用可以在电网与可再生能源之间起缓冲作用,平滑可再生能源的自然可变性,保证电网频率的稳定性,从而提高可再生能源的发电效率和电网接纳可再生能源的能力。
电动汽车-电网互动技术(vehicle-to-grid, V2G)是基于电动汽车与电网间的双向能量交换,探讨电动汽车入网协调优化策略的新技术。文献[4]研究了通过优化电动汽车充电与电网间的协调控制来提高电力系统供电可靠性、经济性的可能性;文献[5]研究了电动汽车参与电网调频的控制策略;文献[6]采用分时充电电价对电动汽车充电行为加以引导,实现“削峰填谷”;文献[7]建立了一个经济调度模型,以研究可入网电动汽车充放电行为的随机性和风电出力的不确定性。随着V2G研究的进一步深入,综合考虑电动汽车与可再生能源的协调优化将是一大研究重点,但目前相关研究较少。
电动汽车与可再生能源之间的协调优化,不仅需要考虑电网对安全稳定运行和“削峰填谷”的诉求,还需要考虑电动汽车用户的经济成本,以促进电动汽车的普及。本文针对这一协调优化问题建立多目标协调优化模型,并用算例对该模型进行验证。
1 电动汽车和可再生能源模型
1.1 电动汽车时空充电模型
目前关于电动汽车驾驶特性的相关数据较少,但考虑到电动汽车在行驶规律上与传统燃油汽车并无区别,故可从现有对传统机动车的交通分析报告入手,分析电动汽车的驾驶特性。对英国交通部提供的全国出行调查数据分析表明,机动车日行驶里程d近似服从对数正态分布或Weibull分布。为满足用户出行习惯的多样性,考虑多种出行种类(对应的概率密度函数见表1[8]),采用蒙特卡洛法生成各出行种类下的出行距离
式中:μ和σ分别为正态分布的平均值与标准差,k和c分别为Weibull分布的形状参数和尺度参数。
表1 出行种类百分比及对应概率密度函数

出行种类所占比例/%概率分布函数类型参数通勤16Lognormalμ=3.27,σ=1.02商务3Weibullc=111.75,k=1.27教育11Lognormalμ=2.48,σ=1.16购物20Lognormalμ=2.76,σ=1.18个人事务20Lognormalμ=3.02,σ=1.32访友15Weibullμ=83.81,σ=0.93其余娱乐15Lognormalμ=3.42,σ=1.29
本文的研究基于以下假设:充电基础设施发达,充电地点不局限于居民区,也可以是工商业区等工作地点;用户通常习惯在抵达工作地点或出行结束返回住所后立刻将电动汽车接入电网开始充电。
文献[9]对居民区和工商业区内机动车的出行时间和停放行为进行了统计调查和数据分析。早晨,人们驾车离开居民区前往位于工商业区的工作地点,工商业区迎来上班抵达高峰,车辆停放时间通常为白天08:00—18:00;傍晚,人们驾车驶离工商业区回到住所,居民区迎来出行结束高峰,车辆停放时间通常为晚上18:00—次日07:00。
用户抵达工作地点的时间概率密度函数
式中:ta为用户抵达工作地点的时间,μa=7.97,σa=0.66。
用户出行结束返回住所时间的概率密度函数
式中:tb为用户出行结束返回住所的时间,μb=17.6,σb=3.4。
假设上一次使用前电池为满电量,则电动汽车每日所消耗的电能
式中W为平均能耗,按0.15kWh/km计算。
电能的变化最终体现在电池荷电状态(stateofcharge,SOC)的变化上,充电前电池初始SOC
式中:Cb为电池容量,Ub为电池的标称电压。
对一从给定时刻k开始充电的电动汽车来说,其到时刻t(k≤t)仍在充电的概率
式中N为电池从零电量充至满电量所需时间。
采用锂电池为研究对象,其充电功率可近似看作一定值Pc。为便于数值计算,以Δt为间隔离散化。假设电动汽车在给定时刻k开始充电的概率为Φ(k),Φ(k)由充电控制策略所决定。对于待研究区域电网内的n辆电动汽车,一天内任一时刻t的充电功率平均值
式中:t0为充电开始时间,tend为充电结束时间。
1.2 风电出力模型
风力发电的出力随风速的变化而变化,目前国内外公认的风速分布概率模型为两参数Weibull分布函数,其概率密度函数
式中v为风速。
风力发电机组有功出力与风速之间的关系为:
式中:Pw为风力发电机的实际有功出力,Pr为风力发电机的额定有功出力,vr、vi和vo分别为额定风速、切入风速和切出风速。
1.3 光伏发电出力模型
光伏发电的实际输出功率主要取决于太阳的辐射强度。在一段时间内,太阳辐射的光照强度近似满足Beta分布,其概率密度函数
式中:Γ为Gamma函数,I和Imax分别为光伏电池板倾斜面上的实际光照强度和最大光照强度,α和β为Beta分布的形状参数。
光伏发电的实际输出功率与其接受的太阳辐射强度成正比,单个电池组件的输出功率

式中:A为单个电池组件的面积,η为对应电池组件的光电转换效率。当光伏电池方阵共有N个组件正常工作时,方阵的总输出功率为NP。
2 电动汽车和可再生能源的协调优化模型
2.1 目标函数
电动汽车和可再生能源的协调优化需考虑电网和电动汽车用户两方面的诉求,一方面尽量协调电动汽车和间歇性可再生能源对电网的影响,平抑电网等效负荷波动,降低配电网总损耗;另一方面尽可能地降低电动汽车用户的充电成本,加快电动汽车普及速度。两方面的诉求对电池的充电要求存在一定的冲突性。
优化模型目标具体如下:
a)平抑配电网等效负荷波动,其数学表达式为
其中
式中:F1为配电网等效负荷波动值,Pload,t、Pw,t、Ps,t、Pev,t分别为t时刻电网的原有负荷、风力发电机组出力、光伏发电出力和电动汽车的充电功率,Pav为Pload,t、Pw,t、Ps,t、Pev,t的平均值。
b)配电网总损耗F2最小,其数学表达式为
式中:Rl为线路l的电阻值,Il,t为t时刻流过线路l的电流,lmax为总线路数。
c)电动汽车用户充电成本F3最小,其数学表达式为
式中C(t)为t时刻的电价。
2.2 约束条件
2.2.1 电动汽车电池电量约束
对单台电动汽车而言,电池的充电电量和存储电量应满足如下条件:
式中:t0为充电开始时刻,T为充电持续时间,Qe为电池额定满充电量,Qmin和Qmax分别为电池可存储电量的最小值和最大值,Qt为t时刻电动汽车存储的总电量。
对t时刻内的所有电动汽车而言,应满足如下条件:
其中
式中:μ为电动汽车充电效率,Qcons,t为t时刻所有电动汽车消耗的电量,ε为电动汽车单位里程的平均能耗,Ncons,t为t时刻处于行驶状态的电动汽车数量;Qcons,i,t为t时刻第i辆电动汽车行驶的距离。
2.2.2 充电时间约束
充电时间t限定在电动汽车闲置阶段,即
式中:Tarrive为电动汽车抵达充电地点的时间,Tleave为电动汽车离开充电地点的时间。
2.2.3 电动汽车充电负荷约束
式中:λ1(i)、λ2(i)、λ3(i)分别为表明节点i处的负荷是否属于居民区、工业区或商业区的变量,其值为“1”表示属于,其值为“0”表示不属于;Pr(t)、Pi(t)、Pc(t)分别为t时刻居民区、工业区和商业区有功负荷的标幺值;Pr、Pi、Pc分别为居民区、工业区和商业区的负荷峰值;xi(t)为t时刻接入节点i处开始充电的纯电动汽车(pure electric vehicle,PEV)数量。
2.2.4 系统潮流约束
式中:Ui为节点i的电压,Gi,j、Bi,j、θi,j分别为节点i和j之间的电导、电纳和电压相位差,PG(i,j)、QG(i,j)分别为t时刻节点i的发电机有功出力和无功出力;PL(i,j)、QL(i,j)分别为t时刻节点i的负荷有功功率和无功功率,n为系统节点数量。
2.2.5 电压幅值约束
式中:Ui,t为t时刻节点i的电压值,Uimax、Uimin分别为节点i的电压上限值和下限值。
2.2.6 支路传输功率约束
式中:Slmax为线路l的最大传输容量,Sl为线路l的传输容量。
2.3 多目标优化调度
采用基于量子粒子群优化(quantum-behavedparticle swarm optimization, QPSO)算法的多目标优化算法求解上述多目标优化模型,该算法全局搜索能力强,且粒子状态仅含位置向量,算法参数少,更容易利用编程实现和控制[10]。算法流程如图1所示。

图1 基于QPSO算法的多目标优化算法流程
多目标优化问题通常不存在唯一解使所有目标均最优,其最优解通常为Pareto解,所有Pareto解构成的集合称为Pareto解集。
3 仿真算例
3.1 仿真系统
本文采用IEEE-33节点系统作为仿真对象,该系统为三相平衡系统,单线图如图2所示。三相功率的基准值SB=10 MVA,线电压的基准值UB=12.66 kV。节点1连接到主电网,为参考节点,其余节点均为负荷节点。假定节点2—18为居民区,节点19—25为工业区,节点26—33为商业区,3种典型负荷的标准化日负荷曲线如图3所示。

图2 IEEE-33节点配电网单线图和负荷分区
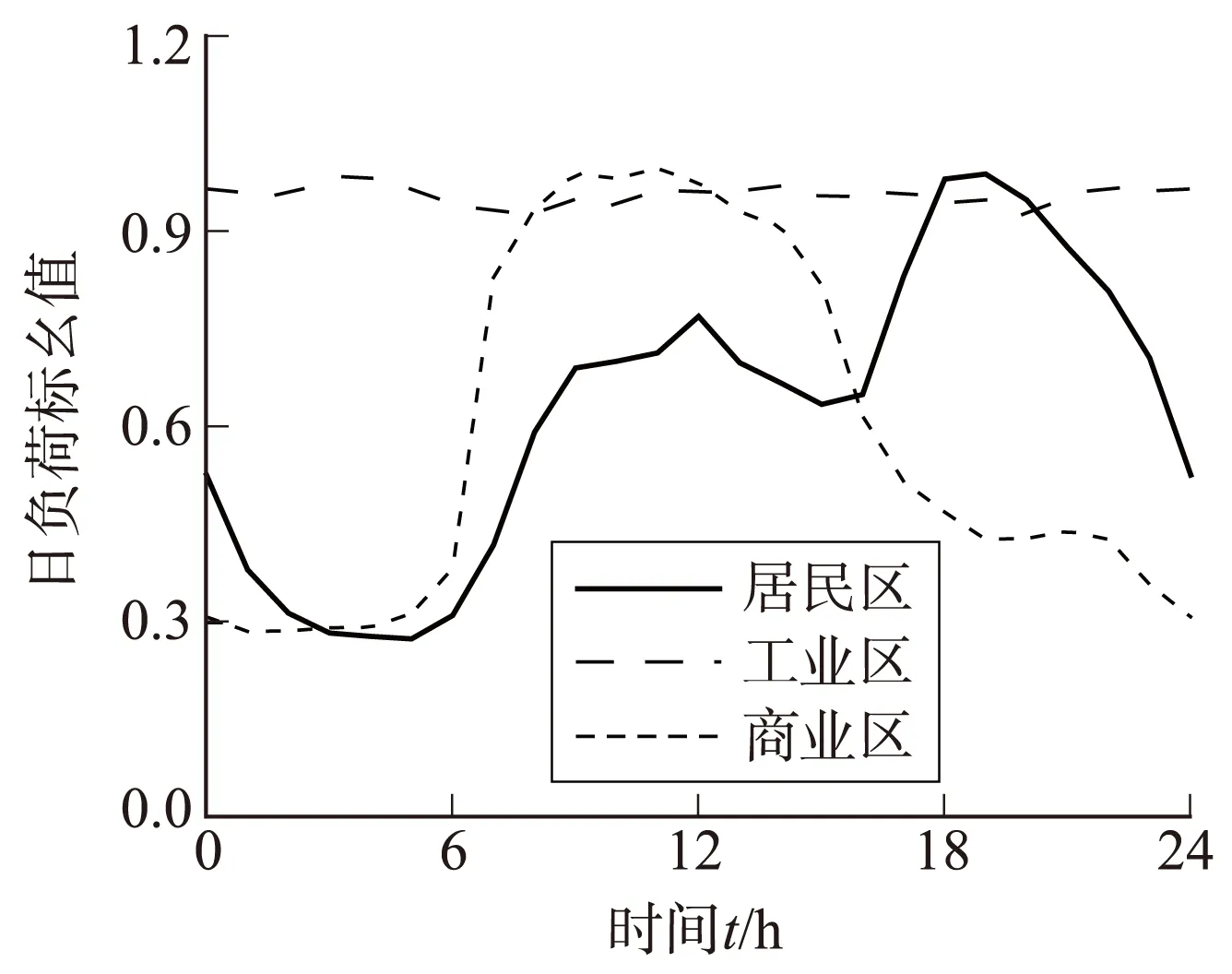
图3 3种典型负荷的标准化日负荷曲线
设定风力发电和光伏发电的最高发电容量比为15%,并在线路的中间偏末端接入电网。风力发电机组4台,为国产FD-24-200型机组,装设在节点18、25、32,分别为2、1、1台;光伏发电400组,光伏方阵型号为SFM144Hx250wp,装设在节点17、24、33,分别为200、100、100组。某风速曲线和光照强度曲线对应的风电和光伏发电有功出力见表2,一天各时刻的购电电价见表3。
表2 风电和光伏发电有功出力

时刻有功出力/kW风电光伏发电时刻有功出力/kW风电光伏发电01:00343.60.013:00335.2325.102:00395.80.014:00302.3408.703:00446.30.015:00253.5343.704:00405.00.016:00214.7185.805:00369.70.017:00180.2102.206:00341.00.018:00202.155.807:00298.146.519:00192.80.008:00321.7102.220:00164.20.009:00321.7195.121:00200.40.010:00350.3288.022:00241.70.011:00291.4260.123:00264.40.012:00335.2250.824:00270.30.0
表3 峰谷分时电价

时段用电状态购电价格/(元·kW-1h-1)00:00—08:00低谷0.36508:00—12:00高峰0.86912:00—17:00平段0.68717:00—21:00高峰0.86921:00—00:00平段0.687
3.2 Pareto最优解
本文建立的协调优化模型目标数为3,设定粒子维数为15,包含住宅区域的9个可充电时刻和工作区域的6个可充电时刻,个体变量即各时刻接入电网充电的电动汽车数量。优化得到的非劣解在目标空间中的分布如图4所示。

图4 Pareto最优解空间分布
从图4可以看出,算法搜索到的非劣解构成了Pareto前沿,整个解集具有较好的分布性。
表4比较了加入风光发电系统前后的最优解。
表4 最优解比较
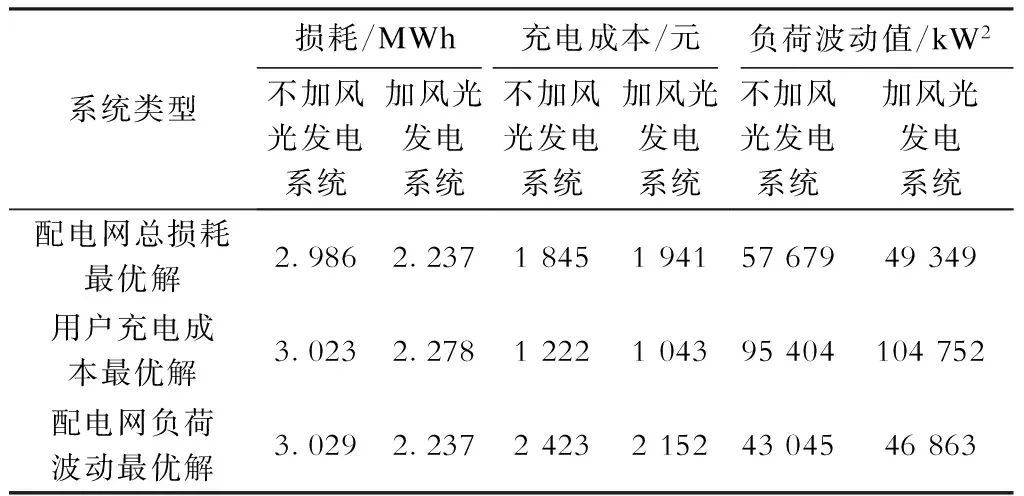
系统类型损耗/MWh不加风光发电系统加风光发电系统充电成本/元不加风光发电系统加风光发电系统负荷波动值/kW2不加风光发电系统加风光发电系统配电网总损耗最优解2.9862.237184519415767949349用户充电成本最优解3.0232.2781222104395404104752配电网负荷波动最优解3.0292.237242321524304546863
由表4可知:配电系统加入风光发电系统后,配电网总损耗最优值从2.986 kWh降到2.237 kWh,降低了25.1%,电动汽车用户充电成本最优值从1 222元下降到1 043元,节省了14.7%,说明风力和光伏等可再生能源的接入不仅减少了配电网损耗,还可降低电动汽车用户的充电成本。
3.3 最终方案
Pareto解集的所有解均是最优解,最终方案的选取可根据实际需求来决定。针对本文考虑的3个目标函数,制定选取原则:首先保证电能质量,确保各节点电压不越限,降低电网的线路损耗;其次降低用户的充电成本,加快电动汽车的普及;最后尽量减少电网等效负荷的波动,提高电网的经济运行。据此,最终方案选取考察目标的优先顺序为F2→F3→F1。各时刻电动汽车入网数量的最终优化结果见表5,对应充电功率曲线如图5所示。
表5 各可入网时刻开始充电的PEV数量的最终方案

时刻入网时刻开始充电的PEV数量百分比/%时刻入网时刻开始充电的PEV数量百分比/%01:001318:00002:001519:00008:00620:00009:001321:00010:00522:00211:00423:00112:001124:00813:0022

图5 电动汽车充电功率曲线
从表5可以看出:13:00和02:00入网开始充电的电动汽车数量较多,并在充电时长内持续消耗电网功率。13:00是白天最后可入网时刻,且工商业区传输线路短、网络损耗小、电压不易越限;02:00是夜晚最后可入网时刻,将充电负荷填入原有负荷的低谷时段。
从表2、表3和图7可以看出:12:00—17:00太阳能发电充足且属于平段电价,该时段充电负荷达到最高峰;00:00—06:00是负荷低谷和电价低谷时段,风力发电出力较高,充电负荷亦较高。充分利用这2个时段,可以有效缓解用电压力,降低充电成本。
为了更好地分析最终方案对电网的影响,加入随机充电模式进行比较。图6为含电动汽车充电的等效负荷曲线。

图6 含电动汽车充电的等效负荷曲线
从图6可看出:随机充电方式下的充电负荷与原有负荷高峰叠加;多目标优化充电方式则充分考虑风光出力变化和充电电价的高低,灵活安排入网电动汽车数量,实现多目标函数值最优。通过潮流计算,统计各时刻各节点电压最低值如图7所示。

图7 各时刻节点电压的最低值
由图7可以看出:在负荷高峰时段,多目标优化充电方式较随机充电方式更不易越限。
图8为平均日网络损耗曲线。
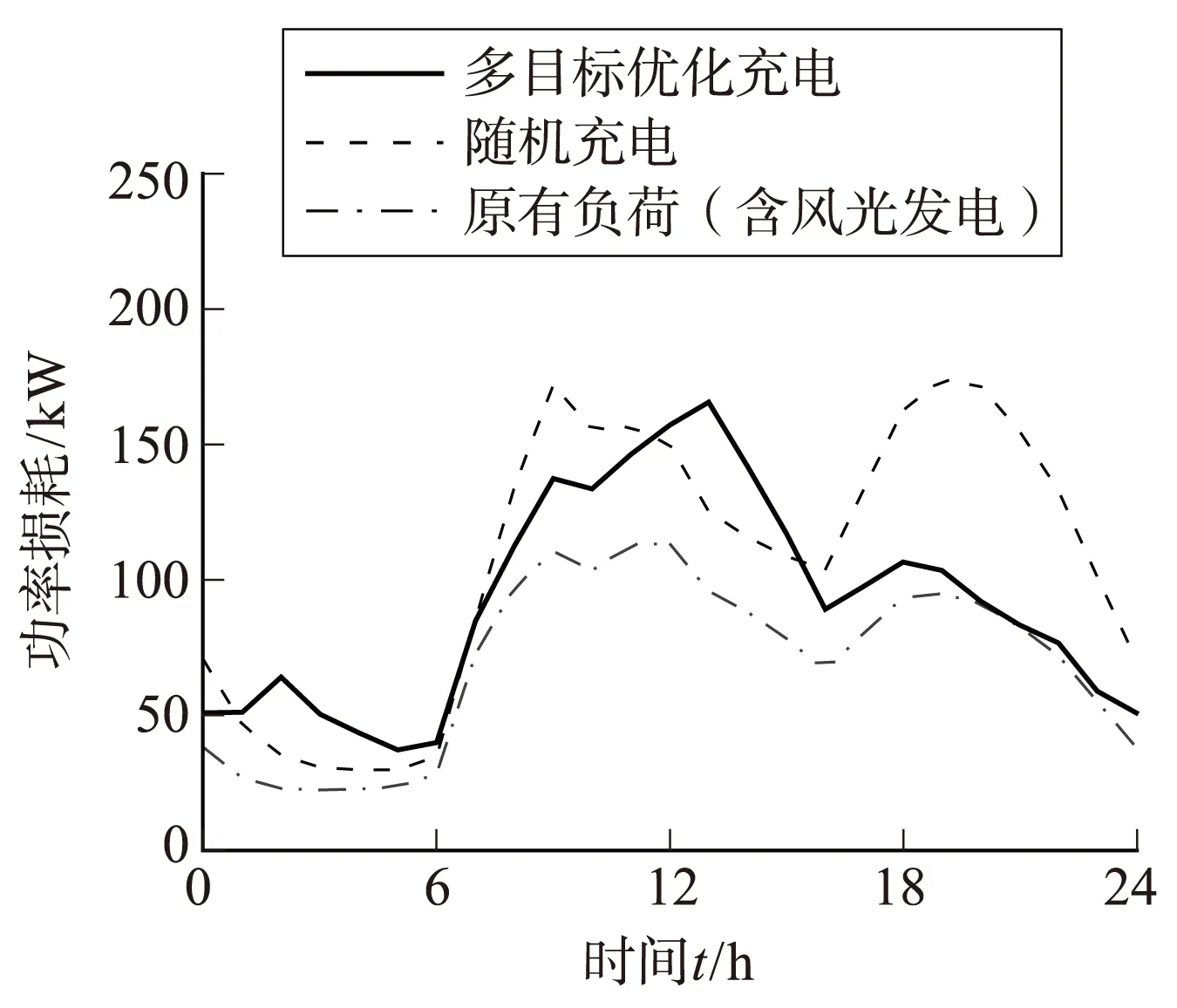
图8 平均日网络损耗曲线
从图8可看出:多目标优化充电方式下,平均日网络损耗曲线与横坐标围成的日网络损耗面积,远小于随机充电方式时,实现了配电网总损耗的优化。
4 结论
本文基于电动汽车时空充电模型和风能、太阳能发电数学模型,建立了电动汽车和可再生能源的多目标协同优化调度方案,在减小间歇性可再生能源对电网冲击的同时,降低了电动汽车用户的充电成本。采用具有更强全局搜索能力的多目标QPSO算法能够获得多种优化调度方案,可根据电网和用户的不同实际需求进行选择。
实例仿真结果表明,该模型可以有效地利用电动汽车电池储能系统作为电网和可再生能源的缓冲,降低可再生能源发电间歇性和电动汽车入网随机性对电网的影响,寻求电网侧和用户侧的双边利益最大化,促进电动汽车的推广普及。
[1] 王锡凡,邵成成,王秀丽,等.电动汽车充电负荷与调度控制策略综述[J].中国电机工程学报,2013,33(1):1-10.
WANG Xifan,SHAO Chengcheng,WANG Xiuli,et al.Survey of Electric Vehicle Charging Load and Dispatch Control Strategies[J].Proceedings of the CSEE,2013,33(1):1-10.
[2] ASHTARI A,BIBEAU E,SHAHIDINEJAD S,et al.PEV Charging Profle Prediction and Analysis Based on Vehicle Usage Data[J].IEEE Transactions on Smart Grid,2012,3(1):341-349.
[3] 荆朝霞,钟童科,林志龙,等.电动汽车充电行为对电网负荷曲线的影响[J].南方电网技术,2013,7(1):80-84.
JING Zhaoxia,ZHONG Tongke,LIN Zhilong,et al.The Impact of Electric Vehicles Charging Behavior on The Load Curve of Power Grid[J].Southern Power System Technology,2013,7(1):80-84.
[4] QIAN Kejun,ZHOU Chengke,ALLAN M,et al.Modeling of Load Demand Due to EV Battery Charging in Distribution Systems[J].IEEE Transactions on Power Systems,2011,26(2):802-810.
[5] MU Yunfei,WU Jianzhong,EKANAYAKE J,et al.Primary Frequency Response from Electric Vehicles in the Great Britain Power System[J].IEEE Transactions on Smart Grid,2013,4(2):1142-1150.
[6] 郑丹,袁泉.采用分时充电电价时电动汽车充电需求分析[J].广东电力,2014,27(12):24-29.
ZHENG Dan,YUAN Quan.Analysis on Charging Demand of Electric Vehicle Based on Application of Time-sharing Charging Price[J].Guangdong Electric Power,2014,27(12):24-29.
[7] 赵俊华,文福拴,薛禹胜,等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化,2010,34(20):22-29.
ZHAO Junhua,WEN Fushuan,XUE Yusheng,et al.Power System Stochastic Economic Dispatch Considering Uncertain Outputs from Plug-in Electric Vehicles and Wind Generators[J].Automation of Electric Power Systems,2010,34(20):22-29.
[8] Department of Transportation. National Travel Survey:2010[R].London:Department of Transportation,2010.
[9] 岳芳.上班出行行为特征研究[D].北京:北京交通大学,2008.
[10] 史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2013:102-107.
(编辑 李丽娟)
Coordinated Optimization on Electric Vehicles and Renewable Energy
ZHOU Yang1,WANG Donghua2
(1. Guangdong Power Grid Development Research Institute Co., Ltd., Guangzhou, Guangdong 510080, China; 2. Guangzhou Bureau, CSG EHV Power Transmission Company, Guangzhou, Guangdong 510405, China)
In allusion to multi-objective coordinated dispatching for electric vehicles and renewable energy, this paper establishes a multi-objective coordinated control model taking minimum load fluctuation of the power distribution network, minimum network loss and minimum charging cost of electric vehicle users for objective functions. It also uses quantum particle swarm(PSO) multi-objective searching algorithm for solution and then gets reasonable network accessing numbers of electric vehicles at each time. IEEE-33 node power distribution system is used for simulating experiment and results indicate that it is able to reduce generation intermittent of renewable energy and influence on the power grid by random of network accessing of electric vehicles by taking battery energy storage system of the electric vehicle as cushion for the power grid and renewable energy, as well as promote maximization of bilateral benefits of grid side and user side.
electric vehicle; renewable energy; coordinated control; quantum particle swarm optimization algorithm; multi-objective optimization
2016-04-27
2016-07-11
10.3969/j.issn.1007-290X.2016.10.008
TM714;TM910.6
A
1007-290X(2016)10-0042-07
周杨(1987),男,湖北荆州人。工程师,工学硕士,从事电网规划与系统分析工作。
王东华(1991),女,江西吉安人。助理工程师,工学硕士,从事直流输电系统运行管理工作。

