一种动态调节惯性权重的粒子群算法

皮倩瑛，叶洪涛*

（1.广西科技大学电气与信息工程学院，广西柳州545006；2.广西汽车零部件与整车技术重点实验室，广西柳州545006）

一种动态调节惯性权重的粒子群算法

皮倩瑛1，2，叶洪涛*1，2

（1.广西科技大学电气与信息工程学院，广西柳州545006；2.广西汽车零部件与整车技术重点实验室，广西柳州545006）

针对使用经典线性递减策略来确定惯性权重的粒子群优化算法在运算过程中与粒子寻优的非线性变化特点不匹配的问题，提出一种动态调节惯性权重的粒子群算法.该算法对惯性权重引入随机因子并基于粒子适应度大小来动态调节惯性权重，更好地引导粒子进行搜索，平衡了算法的全局搜索与局部搜索能力，提高了算法的收敛精度.为了验证该算法的寻优性能，通过8个经典测试函数将标准粒子群算法、惯性权重递减的粒子群算法及动态调节惯性权重的粒子群算法在不同维度下进行测试比较.结果表明：提出的动态调节惯性权重的粒子群算法在寻优精度和成功率方面都有所提升，算法性能更具优越性.

粒子群算法；动态调节；惯性权重；随机因子

0　引言

粒子群优化（Particle Swarm Optimization，PSO）算法最早是由Kennedy和Eberhart于1995年提出的一种群体智能算法［1］，其基本思想起源于对鸟类群体捕食行为的研究，并将社会学中的竞争与合作引入到优化问题的求解中.自PSO算法提出以来，由于它在多峰值、非线性和不可微等一系列优化问题上有着良好的寻优表现，引起了众多学者的关注和研究；又因PSO算法程序简洁易懂、可调参数少，出现了多种改进PSO算法的方法，并被成功应用于多个科学领域.文献［2-3］将改进后的PSO算法分别应用到时变解耦模糊滑膜控制和光伏阵列系统中，拓宽了PSO算法的应用领域.

对PSO算法中可调参数的研究，在目前的改进技术中研究最多的是关于惯性权重因子ω的取值问题，它主要是种群在全局搜索和局部搜索能力之间的一种权衡.由Shi和Eberhart首次在文献［4］中引入惯性权重的概念，为解决粒子爆炸问题取得了重大的进展；后来，Shi等［5］提出了一种基于惯性权重ω线性递减的粒子群优化（linearly decreasing weight PSO，LWPSO）算法，其满足了算法在搜索初期全局搜索能力强、在搜索后期局部搜索能力强的需求，对惯性权重的研究产生了深远的影响.陈贵敏等［6］在惯性权重线性递减的基础上，又提出了3种非线性的权值递减策略；同时，自适应策略［7］、模糊规则策略［8］、混沌策略［9］、指数型策略［10］等不同惯性权重的策略也相继被提出.

受经典线性递惯性权重思想的启发，为了更好地平衡全局搜索能力和局部搜索能力，本文提出一种动态调节惯性权重的策略，由随机因子动态调节惯性权重，并通过适应度函数的引导使粒子更好地进行寻优搜索.通过8个测试函数对标准PSO，LWPSO和该方法进行仿真实验，测试结果表明：该方法较前2种PSO算法有更优越的寻优性能.

1　PSO算法原理

PSO算法源于对鸟类捕食行为的研究.鸟类捕食时，最简单有效的方式就是寻找距离食物最近的鸟的周围区域.PSO首先在可行解中初始化一群粒子，每个粒子都代表该优化问题的一个潜在最优解，每个粒子对应一个由适应度函数决定的适应度值，用速度、位置和适应度值表示该粒子的特征.假设在一个D维的搜索空间中有m个粒子，其中第i个粒子的位置向量为Xi=（Xi1，Xi2，…，XiD），第i个粒子的速度向量为Vi=（Vi1，Vi2，…，ViD）.在PSO算法的进化过程中，个体极值为个体所经历位置中计算得到的适应度值最优位置，记为Pi=（Pi1，Pi2，…，PiD），群体极值为种群中所有粒子寻找到的适应度最优位置，记为Pg=（Pg1，Pg2，…，PgD）.在迭代过程中，每个粒子都会根据个体极值、群体极值和自己前一时刻的速度状态来更新自身的速度和位置，位置和速度更新公式如下［11］：

其中，i＝1，2，…，m；d＝1，2，…，D；ω为惯性权重，在标准PSO算法中一般设置为在区间［0.8，1.2］之间的一个常数；r1，r2是分布于［0，1］区间上的随机数；c1，c2为加速因子，是2个非负的常数；Pid是第i个粒子的个体极值；Pgd是整个粒子群的群体极值是第i个粒子的当前位置是第i个粒子的当前速度.粒子速度更新公式（1）主要由记忆项、自我认知项和社会认知项3部分组成.其中为记忆项，反映了前一次粒子速度的方向、大小对本次速度更新的影响，粒子按原始方向飞行的趋势,起到了局部开发与全局搜索的能力为自我认知项，是由当前粒子指向个体极值的一个矢量，反映了算法中的粒子本身记忆对寻优结果的影响，使粒子具有全局搜索能力为社会认知项，是由当前粒子指向群体极值的一个矢量，群体信息对粒子个体的影响由此反映，它表示了算法中粒子向整个搜索空间中在迭代过程中曾经找到的最优位置进行寻优的趋势，本质上体现了粒子间协同合作［12］.

2　动态调节惯性权重的PSO算法

惯性权重ω是PSO优化算法的可调参数中最重要的参数之一，其大小控制了迭代过程中历史因素对当前状态的影响程度.PSO算法中惯性权重确定从最初的依赖经验到对各种策略的初步探索取得了一定的成效.在大多数PSO算法改进中，学者偏向使用简单、直观的惯性权重线性减小的方法，即惯性权重随着算法迭代次数的增加而线性减小.ω满足公式：

这种方法自提出来虽被广泛应用于各类优化问题之中，但由于在实际的寻优过程中，算法迭代进化是复杂且为非线性变化的，让ω单纯呈线性减小的方式并不能很好地与真实寻优过程相匹配.假设将惯性权重设定为服从某种分布的随机数，并根据粒子适应度大小做出选择，惯性权重受随机因子影响而动态地调整，使算法不仅具有跳出局部最优的机会，还能提高算法的全局搜索性能；因此，在一定程度上，随机因子可以从2个方面来克服算法在进化过中惯性权重随迭代次数线性递减所产生的影响.对比惯性权重线性递减的方法来说：第一，随机因子使得粒子能在搜索初期有机会取到较小的惯性权重，加速算法的收敛；第二，随机因子又能在搜索后期有机会取到较大的惯性权重，提高算法收敛精度.若在搜索前期，粒子已在最优解附近时，与线性递减策略产生的权值相比较，随机分布的惯性权重有机会产生相对小的值，在2种不同权值情况下，后者的粒子适应度比前者的粒子适应度小，算法会选择随机分布产生的惯性权重，此时相对小的惯性权重有利于增强算法的局部搜索能力，加快算法的收敛速度；如果随机分布的惯性权重产生了相对大的值，计算函数的适应度值时，算法则会将随机分布产生的权值淘汰，并选择线性递减策略产生的权值.同理，若在搜索后期，粒子依然与最优解的距离较远时，随机分布的惯性权重有机会产生相对大的值，此时相对大的惯性权重有利于增强算法的全局搜索能力，提高算法的寻优精度；如果随机分布的惯性权重产生的值较小，算法则会将其淘汰.

基于以上分析，提出动态调节惯性权重ω的生成公式：

其中，ω0满足式（3），n为服从正态分布，其均值为1，标准差为0.01.

本算法综合考虑了粒子适应度（Fitness）和随机分布（Random distribution），简称为FRPSO算法.具体流程如下：

Step1先对粒子进行随机初始化，使每个粒子都具有初始速度Vid和初始位置Xid，其中i∈［1,m］，m为粒子个数，d∈［1,D］，D为粒子的维数，取值约束在设置范围内；

Step2将测试函数的函数值设置为粒子的适应度值，根据测试函数计算初始粒子的适应度值，并寻找个体极值Pi和群体极值Pg；

Step3根据式（3）、式（4）计算2种不同的惯性权重ω0和ω1；

Step4根据式（1）、式（2）更新不同惯性权重下的粒子位置和粒子速度，并检查更新后的位置Xid和速度Vid是否越界；

Step5计算、比较2种新粒子的适应度值fitness0和fitness1，若fitness0比fitness1好，则算法选择随机分布的惯性权重，并对新粒子进行个体极值和群体极值的更新.反之，若fitness1比fitness0好，则算法淘汰随机分布产生的惯性权重，选择按式（3）计算的惯性权重，对粒子进行个体极值和群体极值的更新；

Step6若运行次数达到预设最大迭代寻优次数，算法停止并输出全局最优解.否则，返回Step3继续搜索.

3　仿真实验及分析

3.1测试函数

为了测试FRPSO算法对搜索性能的改善，采用8个典型测试函数进行对比分析.测试函数的维数、变量取值范围和目标值如表1所示.8个测试函数的具体数学描述如下：

a）f1为Rastrgin函数

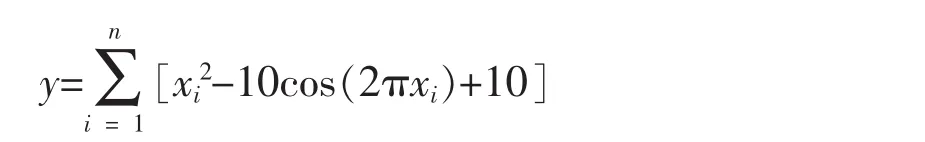
多峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f1（x）=0.

b）f2为Griewankan函数

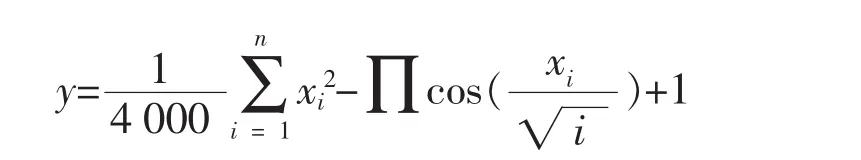
多峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f2（x）=0.

c）f3为Sphere函数

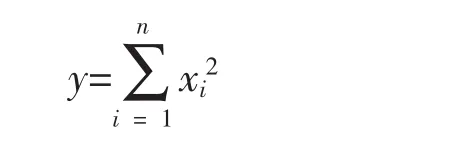
单峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f3（x）=0.

d）f4为Rosenbrock函数

单峰函数，全局最优点在xi=1，i=1，…，n，目标函数最优值是f4（x）=0.

e）f5为Schaffer函数

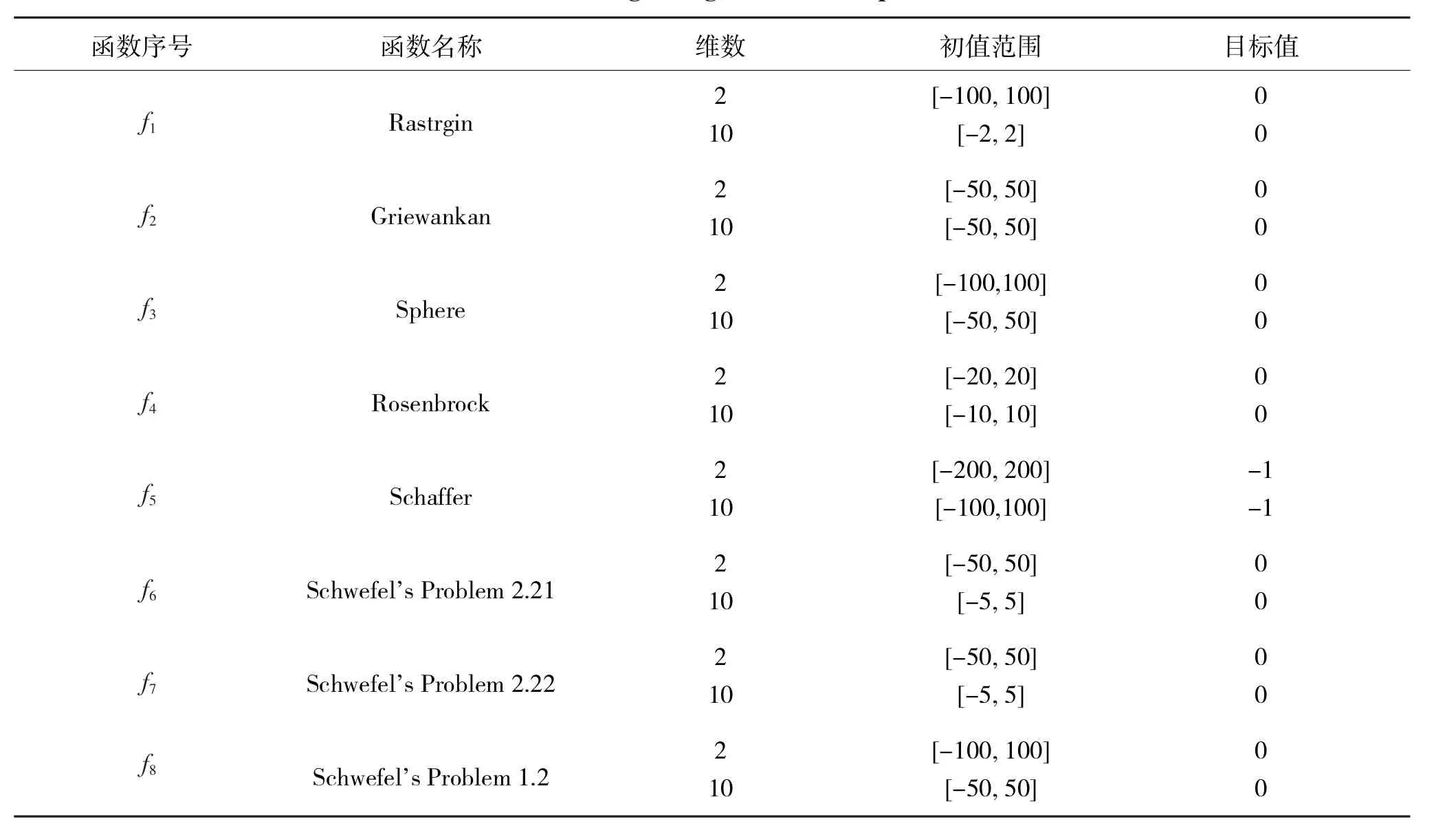
表1　测试函数的维数、初值范围、目标值和期望值Tab.1 The dimension，initial value range，target value and expected value of the test function

多峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f5（x）=-1.

f）f6为Schwefel’s Problem 2.21函数

单峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f6（x）=0.

g）f7为Schwefel’s Problem 2.22函数

单峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f7（x）=0.

h）f8为Schwefel’s Problem 1.2函数

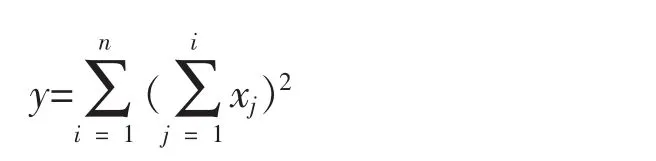
单峰函数，全局最优点在xi=0，i=1，…，n，目标函数最优值是f8（x）=0.

3.2算法测试及分析

将提出的FRPSO算法与标准PSO，LWPSO算法进行比较.对算法的参数取值设置如下：粒子群的种群规模m＝20，学习因子c1＝c2＝1.494 45，最大迭代次数为300.在标准PSO算法中，惯性权重ω=1；在LWPSO算法与FRPSO算法中，ωstart＝0.9，ωend＝0.4.3种不同算法分别独立运行50次，并对这50次所得结果进行统计，计算3种算法的成功率（成功率为迭代寻优结束时，结果值小于给定精度的次数与运行次数的百分比）和适应度值的平均值.表2给出了不同维度下标准PSO，LWPSO和FRPSO算法的实验结果数值.

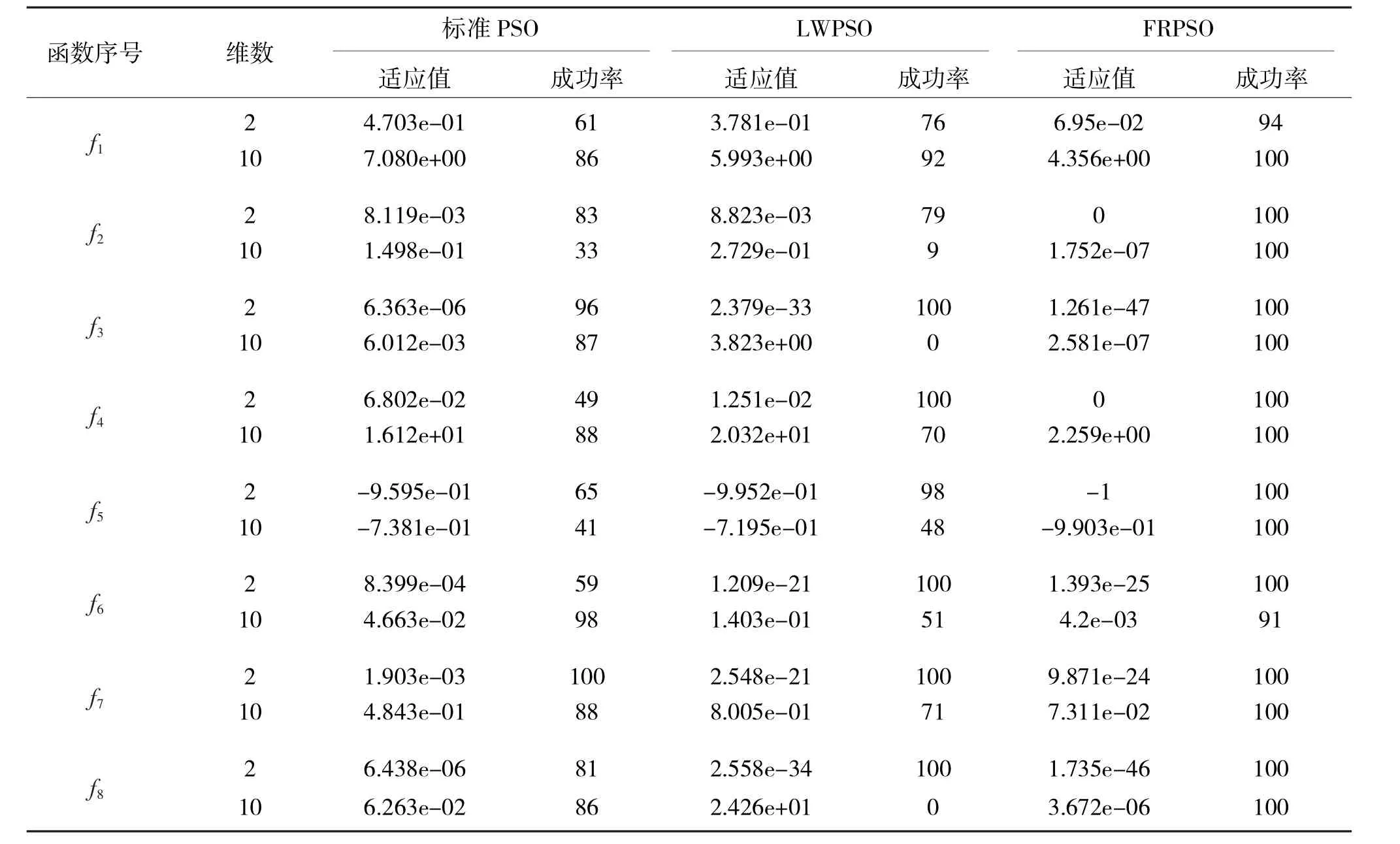
表2　3种算法运行50次的平均适应值与成功率Tab.2 Average fitness and success rate of 3 algorithm s running 50 times

从仿真结果不难看出，对函数f1来说，不管在二维还是十维函数下，LWPSO算法的寻优结果都较标准PSO算法好，但两者结果都不如FRPSO算法.对函数f2来说，不管在二维还是十维函数下，LWPSO算法的寻优结果都较标准PSO算法差，且两者结果远不如FRPSO算法.对函数f3~f8来说，在二维函数情况下，LWPSO算法的寻优结果较标准PSO算法好；在十维函数情况下，标准PSO算法寻优结果较LWPSO算法好.但在2种维度下，FRPSO算法的寻优结果比标准PSO，LWPSO算法的寻优结果都好.特别是对函数f3，f8来说，FRPSO算法的寻优精度大大提高.由于篇幅限制，此处给出测试函数f1、测试函数f3分别在二维函数、十维函数下2种不同维度的收敛曲线图，分别如图1～图4所示.从图中可以明显看出，本文提出的FRPSO算法在不同维度下对比另外2种PSO算法来说，具有更高的收敛精度.

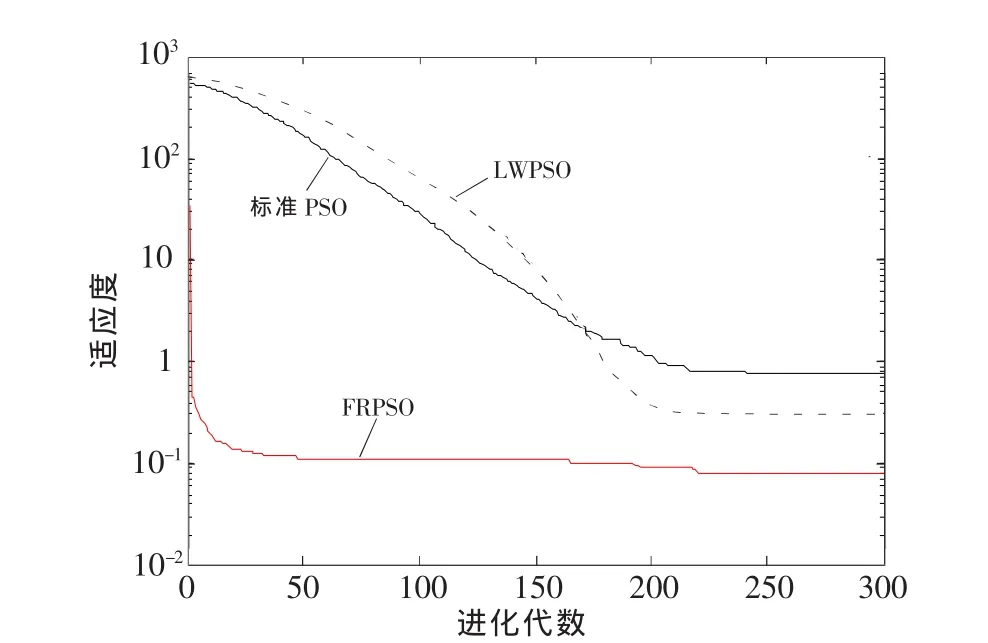
图1　二维Rastrgrin函数收敛结果对比Fig.1 Comparison of convergence results for 2 dimensional Rastrgrin functions

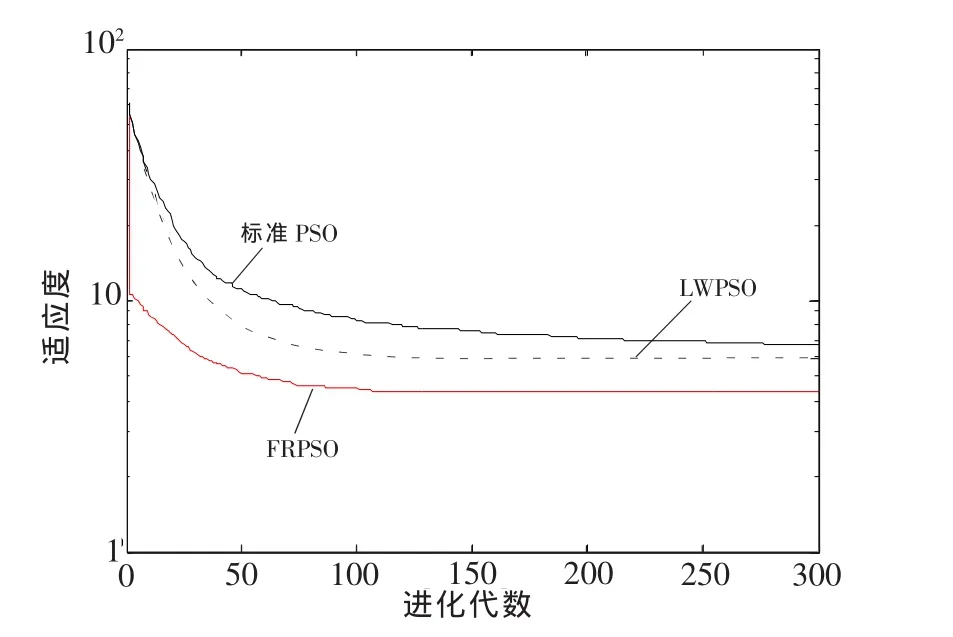
图2　十维Rastrgrin函数收敛结果对比Fig.2 Comparison of convergence results for 10 dimensional Rastrgrin functions

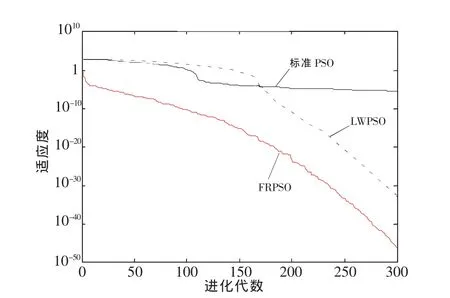
图3　二维Sphere函数收敛结果对比Fig.3 Comparison of convergence results for 2 dimensional Sphere functions

图4　十维Sphere函数收敛结果对比Fig.4 Comparison of convergence results for 10 dimensional Sphere functions

4　结语

本文通过引入随机因子对PSO算法的惯性权重进行动态调节，取得了算法在全局搜索与局部搜索之间的平衡，提出一种动态调节惯性权重的PSO算法.该算法突破经典惯性权重呈线性递减的约束，使算法根据粒子适应度大小来选择惯性权重.仿真结果证明，本文提出的FRPSO算法相比标准PSO算法和LWPSO算法而言，FRPSO算法的寻优性能有明显改善，提高了算法的收敛精度.

［1］KENNEDY J，EBERHART R.Particle Swarm Optimization：IEEE International Conference on Neural Networks，1995［C］.Perth：IEEE，1995.

［2］李哲明，李春贵，吕少姣.基于混沌粒子群优化的时变解耦模糊滑模控制［J］.广西工学院学报，2013，24（3）：67－72.

［3］陈阳，唐培和，徐奕奕.结合混沌粒子群的分布式最大功率点跟踪［J］.广西科技大学学报，2015，26（2）：41－46.

［4］SHIY，EBERHART R.A Modified Particle Swarm Optimizer：IEEE World Congress on Computational Intelligence，1998［C］.Anchorage：IEEE，1998.

［5］SHIY，EBERHARTR.Empirical Study of Particle Swarm Optimization：Evolutionary Computation，1999［C］.Washington：IEEE，1999.

［6］陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究［J］.西安交通大学学报，2006，40（1）：53－56，61.

［7］DONG C，WANG G，CHEN Z，et al.A Method of Self－Adaptive Inertia Weight for PSO：Computer Science and Software Engineering，2008 International Conference on，2008［C］.Wuhan：IEEE，2008.

［8］LIU C，OUYANG C，ZHU P，et al.An Adaptive Fuzzy Weight PSO Algorithm：International Conference on Genetic and Evolutionary Computing，2010［C］.Shenzhen：IEEE，2010.

［9］LIANG J，CAIQ，CHU ZL，etal.Bayesian Network Structure Learning Algorithm Using Particle Swarm Optimization［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2012，40（12）：44－48.

［10］EMEMIPOUR J，NEJAD M，EBADZADEH M.Introduce a New Inertia Weight for Particle Swarm Optimization：Computer Sciences and Convergence Information Technology，2009［C］.Seoul：IEEE，2009.

［11］SHI Y，EBERHART R.Fuzzy Adaptive Particle Swarm Optimization：Evolutionary Computation，Proceedings of the 2001 Congress on，2001［C］.Seoul：IEEE，2001.

［12］赵远东，方正华.带有权重函数学习因子的粒子群算法［J］.计算机应用，2013，33（8）：2265－2268.

（学科编辑：黎娅）

Particle swarm optimization algorithm for dynamic adjustment of inertia weight

PI Qian-ying1，2，YE Hong-tao*1，2
(1.School of Electrical and Information Engineering,Guangxi University of Science and Technology, Liuzhou 545006,China;2.Guangxi Key Laboratory of Automobile Components and Vehicle Technology,Liuzhou 545006,China)

In PSO,the inertia weight is a critical parameter,its role is to balance algorithm global and local search capabilities.For the use of classical linear decreasing strategy to determine the inertia weight particle swarm optimization during operations and optimization of nonlinear changes in particle characteristics mismatch problem, a dynamic adjustment of inertia weight particle swarm algorithm is proposed.The algorithm introduces random inertia weight factor,dynamically adjusts inertia weight based on particle size fitness,better guides the particle search and balances global and local search capabilities so as to improve the convergence precision.In order to verify the performance of the optimization algorithm,by 8 classic test function PSO,decreasing inertia weight particle swarm algorithm and dynamic adjustment of inertia weight particle swarm algorithm were tested in comparison with different dimensions.The results show that the proposed dynamic adjustment of inertia weight particle swarm optimization algorithm in accuracy and success rates have improved,the performance of the algorithm is more advantageous.

particle swarm optimization;dynamic adjustment;inertia weight;random factor

TP301.6

A

2095-7335（2016）03-0026-07

10.16375/j.cnki.cn45-1395/t.2016.03.005

2016-04-13

广西重点实验室项目（14-045-44）；广西教育厅科研项目（201202ZD071）；广西工学院博士基金项目（院科博11Z09）资助.

叶洪涛，博士，教授，研究方向：智能优化与控制，E-mail：yehongtao@126.com.