基于惯性半径相似岸桥模型的地震试验

李 哲， 王贡献， 胡吉全， 王 东

(武汉理工大学物流工程学院 武汉，430063)



基于惯性半径相似岸桥模型的地震试验

李 哲， 王贡献， 胡吉全， 王 东

(武汉理工大学物流工程学院 武汉，430063)

岸桥结构进行缩尺模型设计时，各构件(梁)的几何尺寸可由原形的尺寸按相似比推导出来， 梁截面厚度却不能和长度按同一比尺缩小，导致梁截面尺寸不能完全相似。笔者采用截面惯性半径相似的方法控制抗弯刚度设计梁截面尺寸。以该方法为参考制作了一台岸桥缩尺模型并进行地震试验，缩尺模型试验测量值与数值计算结果接近，结构各考察点加速度、应变出现极值的大小以及所对应的时间都比较接近。该缩尺模型能替代完全相似模型，所得试验值能近似反映实际结构在地震中的动态响应，验证了截面惯性半径相似模型设计方法的可行性，为工程中大型钢结构缩尺模型的设计及后续的地震试验研究提供了参考。

惯性半径； 相似理论； 岸桥结构； 缩尺模型； 振动台试验

引 言

缩尺模型试验现在已经成为大型结构动力学研究过程中不可或缺的部分。以结构动力相似理论为依据设计制作与实际结构尺寸相似而按一定比尺缩放的试验模型[1-2]，对模型进行一系列动力试验，将所得的试验数据按一定的相似比进行换算，即可得到能近似反映实际结构的动态响应参数。

岸桥模型地震试验中最主要的问题在于其结构中梁截面的厚度不能按统一相似比缩放。岸桥梁截面厚度平均在10～25 mm之间，如果尺寸相似比定为1∶50，则缩尺模型中梁截面厚度应为0.2～0.5 mm才能满足梁截面完全相似。0.2～0.5 mm厚度角钢的焊接在实际加工中是极难实现的，工程上一般采用加厚的角钢(2～3 mm)进行焊接，这样得到的缩尺模型和原型就不能完全相似，无法通过缩尺模型预测原型的动态特性。现有的岸桥相似模型设计过程中，为应对梁截面不能完全相似的情况纷纷采取一些措施，如文献[3]设计制作了一个相似比为1∶15的岸桥畸变模型(其梁截面厚度没有按统一的相似比例进行缩放)，采用有限元预测系数法，得到畸变模型动响应预测系数，实现用畸变模型预测原型结构的动态响应。虽然该方法得到的结果准确可靠，但是畸变预测系数必须经过大量的有限元计算推导，还需要相应的试验进行验证，操作起来复杂繁琐、周期长。文献[4]设计制作了1∶20的岸桥缩尺模型，采用质量补偿法对模型进行修正来应对模型不完全相似的问题，在此基础之上他们进行了一系列的地震模拟试验。这套方案根据动力相似原理，对试验模型进行了质量修正，计算出所需添加的质量，并将质量块通过焊接、捆绑等方式加在模型上，质量块的安放位置主要依据试验人员的经验，对于安放了质量块的地方产生局部应力加大以及刚度变化问题未进行考虑，使得部分测量结果产生较大偏差。

现有的研究表明，结构的变形主要是弯曲变形的可选用抗弯刚度作为相似比控制参数，而对于剪切变形为主的结构，选用抗剪刚度作为相似比控制参数更为妥当。大量地震灾害分析表明，岸桥结构地震激励下的破坏形式主要是梁的弯曲变形。笔者经过大量的有限元数值计算以及简单梁架结构的振动试验，得出岸桥结构在地震激励下以立柱的弯曲振动为主，由此可以选用抗弯刚度作为相似比控制参数。现采用截面惯性半径相似的方法，设计出岸桥结构弯曲梁的截面参数，使岸桥理想试验模型结构与实际加工出的试验模型截面惯性半径误差达到最小。以岸桥模型相似比尺的量纲分析为基准，结合梁截面惯性矩公式推导出缩尺模型梁截面的尺寸，制作1∶15的岸桥缩尺模型。建立岸桥结构1∶15完全相似缩尺模型的有限元数值模型、以加工出来的试验缩尺模型为基准的有限元模型以及岸桥原型有限元模型。对试验缩尺模型进行振动台地震模拟试验，配合有限元数值计算来验证截面惯性半径相似模型设计方法的正确性。

1 模型相似比尺分析

笔者研究对象为某港口正在使用的一款俯仰式集装箱岸桥起重机，工作时臂架放下总长达66 m，净高54 m、整机重量约为630 t。根据振动台台面大小(1.5 m×1.5 m)、振动台最大搭载质量(2 t)以及试验场所的空间限制， 尺寸相似比取1∶15。简化了的岸桥结构包括：海陆侧门腿立柱、横梁及撑杆、前后大梁、拉杆等，结构示意图见图1。选取与岸桥原型结构相同的材料Q345钢，其材料弹性模量取值E=206 GPa，泊松比取值ν=0.3，材料密度取ρ=7 850 kg/m3。

图1 集装箱岸桥结构模型Fig.1 Structural model of the quayside container crane

结构动力学性能最直接的表现是：频率、变形、位移[5]。在岸桥结构地震模拟试验中，缩尺模型相关参量应选取：弹性模量E、密度ρ、几何尺寸l、时间t、位移u、速度υ、加速度a、重力加速度g、应力σ、频率ω。在线弹性范围内[6]，采用量纲分析法得到这些参量的函数表达式

(1)

用C来表示岸桥模型与原型之间参量的相似比，如前文所述，几何比尺为：Cl=1/15。缩尺模型的制作材料和原形相同，所以密度比尺Cρ=1、弹性模量比尺CE=1，将这三项作为基本比尺，推导时间比尺Ct、质量比尺Cm、位移比尺Cu、速度比尺Cv、加速度比尺Ca、频率比尺Cω、应变比尺Cε、应力比尺Cσ。梁弯曲振动的微分方程为

(2)

其中：A为梁的截面面积；I为梁的截面惯性矩。

由式(2)推导得出：

(3)

其中：CA为截面面积比尺；CI为截面惯性矩比尺。

由上述推导可得岸桥结构动力模型相似关系如表1所示。

表1 缩尺模型相似关系

2 截面惯性半径相似模型设计

岸桥结构在地震下的响应以梁的弯曲振动为主，梁的弯曲刚度可以通过截面惯性半径来控制(I=r2A)[7]。岸桥原型梁截面和缩尺模型的梁截面示意图分别如图2(a，b)所示。正确设计梁截面参数，使原型梁截面惯性半径与缩尺模型梁截面惯性半径的相似误差达到最小，对提高缩尺模型的精度至关重要。

图2 岸桥原型梁截面与缩尺模型梁截面Fig.2 Cross-sectional shapes of bending beam components of prototype and scale mode

由截面惯性矩公式可得原型与缩尺模型绕y轴的梁截面惯性矩

(4)

(5)

其中：Iyp，Iym分别为原型与缩尺模型绕y轴的梁截面惯性矩；L，H，t1，t2分别为原型的梁截面长度、宽度、左右厚度及上下厚度；Lm，Hm，tm为缩尺模型的梁截面长度、宽度及厚度。

原型与缩尺模型绕z轴的梁截面惯性矩Izp与Izm也可按截面惯性矩公式给出，形式与式(4)，(5)一致。结合截面惯性半径的公式r2=I/A可以得到

(6)

(7)

其中：ryp，rym，rzp，rzm为原型与缩尺模型绕y，z轴的梁截面惯性半径；Ap，Am为梁截面面积;Cry，Crz为绕y，z轴的梁截面惯性半径比尺，均为1/15。

在缩尺模型截面尺寸设计中，首先确定加工钢板厚度tm，再基于式(6)及(7)计算出梁截面的参数Lm和Hm。由于岸桥结构梁构件多、方程复杂、计算量大，故使用通用数学与工程计算软件maple编写计算程序，方程没有精确解。因此，基于工程经验在计算前设置好各参数的取值范围，得到的截面参数Lm和Hm的近似解。

以海测立柱为例，梁截面尺寸为：L=0.900 m，H=1.400 m，t1=0.010 m，t2=0.010 m；梁截面惯性半径比尺Cry=Crz=1/15；钢板厚度取tm=0.003 m。将已知参数代入计算程序得到近似解Lm=0.060 24 m，Hm= 0.096 22 m。模型加工精度为毫米级，取Lm= 0.060 m，Hm= 0.096 m。

采用上述设计方法得到的岸桥主要梁截面尺寸如表2所示。(表中Cry′，Crz′为Cry，Crz的倒数，与最初设定值15有细微差别，可忽略不计)

表2 1∶15缩尺模型弯曲梁构件的截面参数

Tab.2 Cross-sectional parameters of bending beam components of 1∶15 scale model

弯曲梁名称截面参数/mm惯性半径比尺(倒数)LmHmtmC'ryC'rz前大梁5757314.8214.82后大梁63102314.8315.05海测立柱6096314.9515.61陆测立柱6096314.9515.61海测横梁63112314.8314.59陆测横梁63123314.8314.92梯形梁6262315.0915.09

3 岸桥结构地震试验分析

3.1 模型仿真分析

使用有限元仿真计算验证截面惯性半径相似模型设计方法的可行性。按原型尺寸建立岸桥有限元模型M1、按1∶15相似比严格缩放的完全相似缩尺模型M2(完全相似缩尺模型)以及一个按截面惯性半径相似模型设计方法设计截面尺寸的缩尺模型M3(弯曲刚度相似缩尺模型)，岸桥结构模型的有限元模型示意图见图3。在采用有限元计算前需对有限元模型进行修正，配合缩尺模型(见图4)模态试验以及加载试验、采用参数型修正法对岸桥有限元模型进行修正，从而提高有限元数值模型精度。在有限元模型修正过程中，通过反复调整各部件材料属性，使得有限元模型与试验缩尺模型前几阶频率振型一致、加载后应力值大小接近[8]，且应通过结构阻尼试验为有限元模型设置合理的阻尼参数[9-10]。

图3 集装箱起重机有限元模型Fig.3 Finite element model of the container crane

图4 试验缩尺模型Fig.4 Scale model of the container crane

首先对有限元模型M1，M2，M3进行模态计算，其计算结果如表3所示，其中模型M2的频率值经过相似比转换后与模型M1完全一致，M3频率值与M2非常接近，但存在着较小的误差，误差在可接受的范围内。模型只比较频率一般是不全面的，应该还要比较振型，考虑到振型图占用篇幅较多，且第1振型占其地震反应的主要部分[11]，这里采用文字描述岸桥模型前3阶振型特征。1阶模态主要振型特征：前大梁扬起、门框沿大梁方向弯曲；2阶模态主要振型特征：门腿沿大梁方向弯曲；3阶模态主要振型特征：后大梁扬起、门框沿大梁方向弯曲。岸桥模型M1，M2前3阶振型特征完全一致， M2与M3振型之间存在细微区别，可忽略不计。模型M2与M3频率、振型产生误差的主要原因包括：截面惯性半径不能完全相似；虽然岸桥结构地震主要以弯曲变形为主，但模型的振型中可能包含构件的剪切变形。模型M2，M3前6阶固有频率接近且前3阶振型特征相似，说明模型M3可以代替完全相似缩尺模型，即采用截面惯性半径相似方法在有限元仿真方面是可行的。

表3 岸桥模型固有频率

Tab.3 The first six frequencies of models

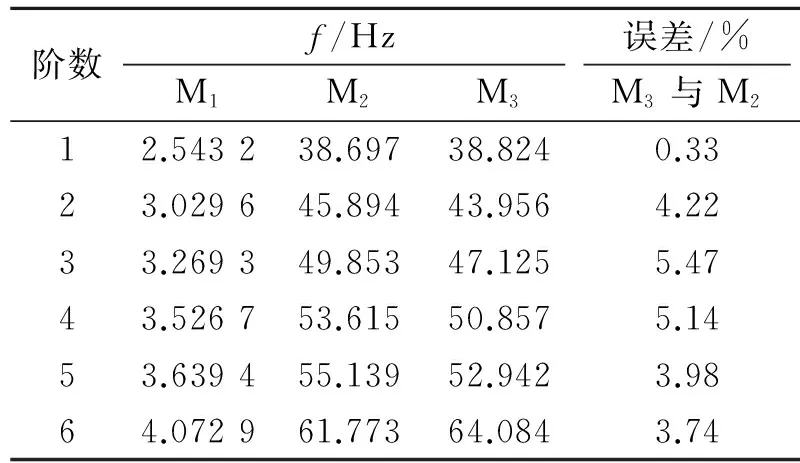
阶数f/Hz误差/%M1M2M3M3与M212.543238.69738.8240.3323.029645.89443.9564.2233.269349.85347.1255.4743.526753.61550.8575.1453.639455.13952.9423.9864.072961.77364.0843.74

进行地震时程分析，取EL-Centro南北向地震加速度记录(20 s,Δt=0.02 s)、Taft东西向地震加速度记录(20 s,Δt=0.02 s)，加速度峰值分别调整为 0.1g，0.2g，对于1∶15缩尺模型而言，地震载荷的时间轴调整为原型的1/15(20 s调整为1.34 s)，而峰值加速度则被调整为1.5g(对应原型的0.1g)，3g(对应原型的0.2g)。图5中A1，A4为加速度考察点，A2，A3为位移考察点，S1～S12为应力应变考察点。

图5 模型测量点Fig.5 Measurement nodes of the model

经对比分析时程计算结果，发现完全相似模型M2的时程计算结果与岸桥原型M1完全一致，这符合实际情况，也验证了数值模型的正确性。故后面分析中将模型M2的值作为基准，对比分析时，只需将M3与M2或者试验值与M2进行对比，这样可以避免相似比换算时产生的误差，结果也更加直观。加速度峰值调整为 0.1g时，EL，Taft波下考察点A1的加速度时程曲线如图6，7所示 (注:实线代表模型M2，虚线表示M3。在EL波下考察点A1的加速度方向为小车运行方向，即南北方向；在Taft波下考察点A1的加速度方向为大车运行方向，即东西方向)。

图6 考察点A1的加速度时程曲线(EL 0.1 g)Fig.6 Acceleration time-history curve at A1(EL 0.1 g)

图7 考察点A1的加速度时程曲线(Taft 0.1 g)Fig.7 Acceleration time-history curve at A1(Taft 0.1 g)

加速度峰值调整为 0.2g时，EL，Taft波下考察点A1的加速度时程曲线如图8～9所示。

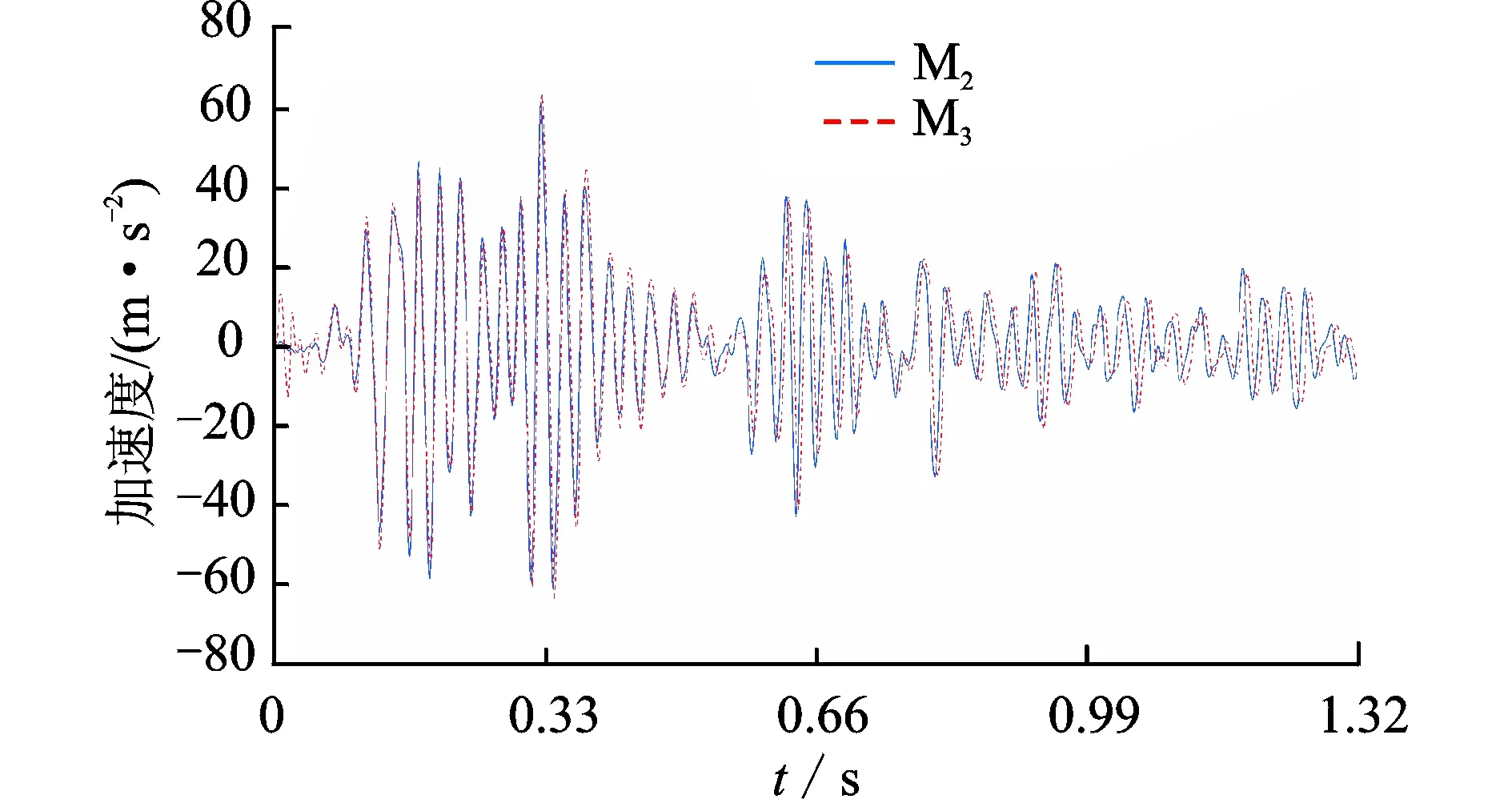
图8 考察点A1的加速度时程曲线(EL 0.2 g)Fig.8 Acceleration time-history curve at A1(EL 0.2 g)

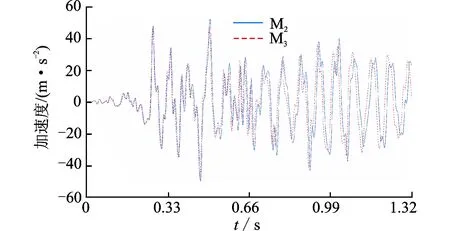
图9 考察点A1的加速度时程曲线(Taft 0.2 g)Fig.9 Acceleration time-history curve at A1(Taft 0.2 g)

考察点A2在地震波EL，Taft加速度峰值调整为 0.2g时位移时程曲线如图10～11所示。

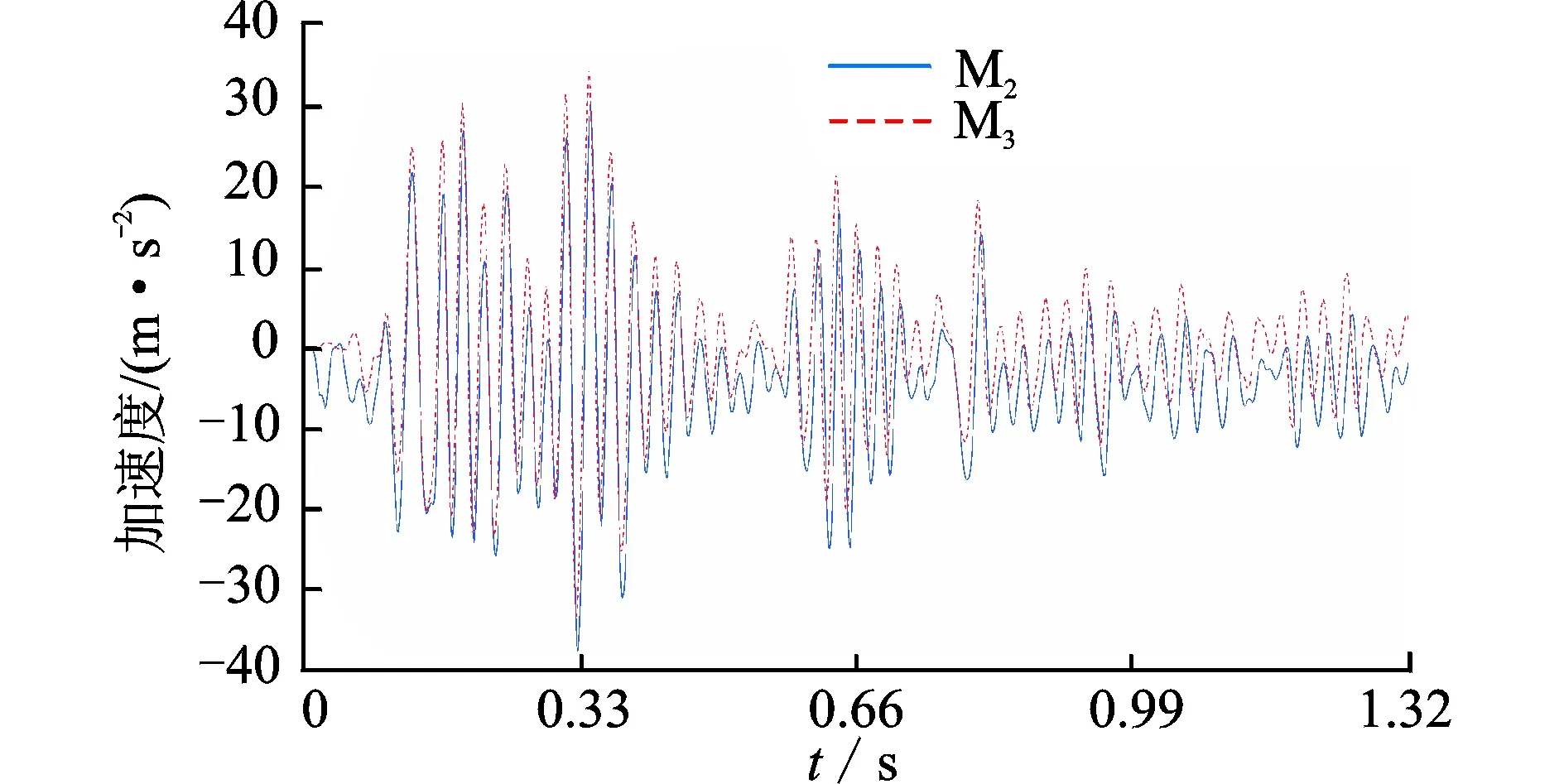
图10 考察点A2的位移时程曲线(EL 0.2 g)Fig.10 Displacement time-history curve at A2(EL 0.2 g)

图11 考察点A2的位移时程曲线(Taft 0.2 g)Fig.11 Displacement time-history curve at A2(Taft 0.2 g)

观察图6～11可以发现，由模型M3计算得到的地震响应与M2的结果十分接近，说明在有限元时程计算中采用截面惯性半径相似方法设计的有限元模型M3代替完全相似模型M2是可行的。在相同地震激励、不同的加速度峰值调整下考察点加速度时程曲线形状相似，0.2g时加速度峰值变化为0.1g时的1.5～2倍，与前期预计的情况相符。

3.2 振动台模型试验

本试验旨在证明采用截面惯性半径相似方法设计的试验缩尺模型能代替完全相似试验缩尺模型(由于完全相似试验缩尺模型无法加工制造，所以与试验值比较的对象为经过修正的有限元模型M2的计算值)。试验位于武汉理工大学港口装卸实验室，所采用的振动台可进行水平方向、垂直方向的任意单方向或组合双向振动试验，台面长宽均为1.5 m，可提供加速度范围为±50 m·s-2，最大位移±200 mm，最大速度均为0.8 m·s-1，最大承载力2 t，频率范围0.1～100 Hz，3 dB带宽。试验中，2个加速度传感器、2个位移传感器、12个应变片(S1～S12)被布置在模型门架结构上如图5所示。按照M3的梁截面参数制造一台试验用缩尺试验模型，对其进行振动台地震模拟试验来验证此相似模型是否可以代替完全相似模型，加工出的试验缩尺模型见图4。

采用文献[12]中介绍的模态测试方法来获取岸桥1∶15缩尺试验模型的固有频率。M2，M3有限元模态计算结果和缩尺模型试验值及相应的误差如表4所示。

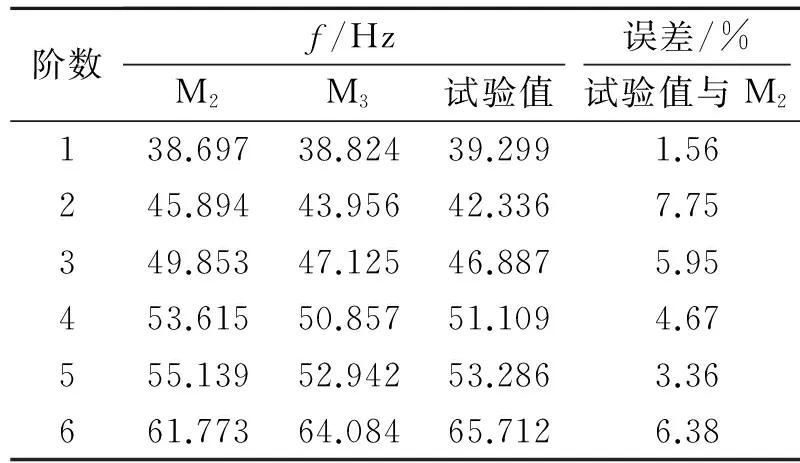
表4 试验模型固有频率

为节约篇幅，只给出考察点A4的加速度时程曲线 (在EL地震波下，加速度峰值调整为 0.2g)。如图12所示，按截面惯性半径相似方法加工出的模型能够较好地预测原型的地震响应。图中实线为模型M2计算值，虚线为缩尺模型试验实测值。

观察对比完全相似模型

M2的计算结果和缩尺

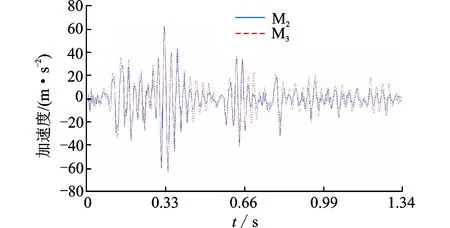
图12 考察点A4的加速度时程曲线Fig.12 Acceleration time history curve at A4

模型试验实测值，在不同地震载荷下、不同加速度峰值调整下岸桥结构上各考察点加速度、应变出现极值的大小以及所对应的时间都比较接近。最大加速度出现在岸桥大梁前后两端，这与试验所测结果一致，也符合实际地震情况下岸桥结构加速度响应；最大的应变主要集中在前大梁与拉杆连接处以及后大梁的中部位置；原型结构的应变分布情况与表5中的应变分布情况接近，说明按照M3截面参数设计加工出的缩尺模型能得到正确可靠的试验数据。

表5 不同测点的最大动态应变

Tab.5 Maximum dynamic strain at various nodes

测点应变(E×10-6)M2试验值误差/%试验值与M2S282.578.64.72S4156.8169.37.97S6206.7211.52.32S9138.3125.39.39S10271.3275.41.51S12307.9313.11.69

完全相似模型M2计算值与试验实测值之间存在微小差异的原因有：a.梁的截面惯性半径相似不可能完全被满足，与设计的15有偏差；b.有限元模型与试验模型存在一些细小的差别；c.传感器测量误差；d.虽然岸桥结构地震主要以梁的弯曲变形为主，但结构的振型中可能包含构件的剪切变形。采用截面半径相似方法设计加工的试验模型的可行性得到了进一步的验证，采用该方法设计加工出的缩尺模型能代替完全相似模型。

4 结 论

1) 采用截面惯性半径相似方法对岸桥梁截面参数进行设计，加工出的1∶15岸桥缩尺模型能代替完全相似模型，准确地预测出原型结构的动态特性和地震响应。

2) 岸桥缩尺试验模型地震试验实测值中频率、振型、加速度、位移以及应变与数值计算结果有较高的相似度，最大误差为9.39%，满足工程需要，该方法能为后续的研究提供精确可靠的试验缩尺模型。

[1] 陈喆，陈国平. 相似理论和模型试验的结构动响应分析运用[J]. 振动、测试与诊断， 2014,34(6)：995-1001.

Chen Zhe, Chen Guoping. Research of dynamics response based on similarity theory and model test [J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(6):995-1001.(in Chinese)

[2] 张莹，孙广俊，李鸿晶.开洞填充墙对混凝土框架柱地震损伤影响分析 [J]. 振动、测试与诊断,2014, 34(5):932-938.

Zhang Ying, Sun Guangjun, Li Hongjing. Numerical simulation on seismic damage of reinforced concrete frame columns considering the influence of infill walls with opening [J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(5):932-938. (in Chinese)

[3] 李哲,胡吉全,王东.地震载荷作用下岸桥结构单参数畸变相似模型研究[J]. 振动与冲击. 2014,33(20)：174-179.

Li Zhe, Hu Jiquan, Wang Dong. Distortion model of container cranes subjected to seismic load[J]. Journal of Vibration and Shock, 2014, 33(20): 174-179.(in Chinese)

[4] Jacobs L D， Des Roches R, Roberto T L. Seismic behavior of a jumbo container crane including uplift[J]. Earthquake Spectra, 2011, 27(3)：745-773.

[5] 何川，汪洋，方勇，等. 土压平衡式盾构掘进过程的相似模型试验[J]. 土木工程学报，2012，45(2):162-169.

He Chuan, Wang Yang, Fang Yong, et al. Similarity model test of earth-pressure-balanced shield tunneling process[J]. China Civil Engineering Journal, 2012,45(2):162-169. (in Chinese)

[6] 金玉龙,吴天行. 集装箱码头岸桥结构的动力相似分析与试验验证[J]. 上海交通大学学报:自然科学版, 2012, 46(10): 1609-1615.

Jin Yulong, Wu Tianxing. Dynamic similarity analysis and experimental verification on a quayside container crane[J]. Journal of Shanghai Jiaotong University：Science, 2012, 46(10): 1609-1615.(in Chinese)

[7] Jin Yulong, Li Zengguang. Theoretical design and experimental verification of a 1/50 scale model of a quayside container crane[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2012, 226(6):1644-1662.

[8] 苏忠亭，徐达，李晓伟，等. 步兵战车车体结构有限元模型修正 [J]. 振动、测试与诊断,2014, 34(6):1148-1155.

Su Zhongting, Xu Da, Li Xiaowei, et al. Finite-element model updating for infantry combat vehicle car-body[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(6): 1148-1155.(in Chinese)

[9] 张教超，王敏庆，马建刚. 结构阻尼的声衰减时间测量方法 [J]. 振动、测试与诊断,2013, 33(2):330-333.

Zhang Jiaochao, Wang Minqian, Ma Jiangang. Approach for determining structural damping by measurement of sound attenuation time[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 330-333.(in Chinese)

[10]张安付，闫孝伟，盛美萍，等. 自由阻尼结构损耗参数的换算方法 [J]. 振动、测试与诊断,2015, 35(3):572-578.

Zhang Anfu, Yan Xiaowei, Sheng Meiping, et al. Conversion method for loss factor of unconstrained damping structures[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 572-578.(in Chinese)

[11]刘世忠. 系杆拱桥的横向振动特性分析 [J]. 振动、测试与诊断,2015, 35(2):245-250.

Liu Shizhong. Analysis of transverse vibration frequency of tied arch bridge[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 245-250.(in Chinese)

[12]孙熙平，王元战，赵炳皓. 环境激励下高桩码头物理模型模态实验[J].振动、测试与诊断，2013，33(2):263-268，340.

Sun Xiping, Wang Yuanzhan, Zhao Binghao. Modal experiment of physical model for high-piled wharf under ambient excitation[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 263-268,340.(in Chinese)

doi:10.16450/j.cnki.issn.1004-6801.2016.05.025

10.16450/j.cnki.issn.1004-6801.2016.05.024

国家自然科学基金资助项目(51275369)

2015-07-08；

2015-09-02

U448.21; TH13

李哲，男，1986年5月生，博士生。主要研究方向为机械工程。曾发表《地震载荷作用下岸桥结构单参数畸变相似模型研究》(《振动与冲击》2014年第33卷第20期)等论文。

E-mail：172042756@qq.com

简介：王贡献，男，1976年12月生，博士、副教授。主要研究方向为结构动力学。

E-mail：wgx@whut.edu.cn