斜齿轮振动噪声分析方法

刘艳芳， 赖俊斌， 岳会军， 徐向阳， 李 晟

(1. 北京航空航天大学交通科学与工程学院 北京，100191) (2. 中国航天科技集团公司北京航天发射技术研究所 北京，100076) (3. Wright State University Department of Mechanical and Material Engineering Dayton，45435,USA)



斜齿轮振动噪声分析方法

刘艳芳1， 赖俊斌1， 岳会军2， 徐向阳1， 李 晟3

(1. 北京航空航天大学交通科学与工程学院 北京，100191) (2. 中国航天科技集团公司北京航天发射技术研究所 北京，100076) (3. Wright State University Department of Mechanical and Material Engineering Dayton，45435,USA)

齿轮啮合传动的不平稳是产生振动噪声的主要原因，需要对齿轮啮合传递的动态过程及其规律进行研究。首先，以自动变速器中一对常啮合斜齿轮为研究对象，分别采用有限元法和切片理论计算斜齿轮的传递误差，用以衡量斜齿轮啮合传动的平稳性。然后，根据齿轮修形的经验公式，确定斜齿轮修形参数的范围。基于切片理论，采用列举法，以降低传递误差波动、改善齿面载荷分布为优化目标，确定最优修形方案。最后，通过分析自动变速器的振动噪声台架实验测试结果，有效地验证了笔者采用的方法及模型的可行性。

斜齿轮; 有限元法; 切片理论; 传递误差; 载荷分布; 修形

引 言

齿轮作为基本的传动元件广泛应用于航空、航天、船舶、汽车等领域，现代齿轮传动正朝着高速、重载和低噪声方向发展。齿轮在高速转动过程中，会受到各种激励产生振动和噪声，而振动和噪声不仅是影响齿轮可靠性、寿命和操作环境的关键因素，更是导致齿轮传动失效的一种主要形式[1]。

目前大量研究表明,齿轮的传递误差是齿轮系统振动和噪声的激励源[2]。Harris[3]提出了静态传递误差的概念，定义了静态传递误差的计算函数，奠定了对传递误差的分析基础。目前传递误差的求解主要包括两种方法：a.建立齿轮啮合的有限元模型，求取齿轮的接触变形获得传递误差[4-5]；b.建立齿轮系统动力学模型，根据齿轮的时变啮合刚度、重合度和阻尼等参数获得传递误差[6-7]。采用有限元方法求解的齿轮传递误差精度很高，但是计算效率很低；而采用齿轮系统动力学模型求取传递误差的方法对齿轮的模型进行简化，得不到精确的解。

齿轮修形可以改善齿轮传动状况，减小振动和噪声[8]。文献[9-10]以改善齿面载荷分布、减小啮合冲击为优化目标对齿轮进行修形优化；文献[5,11-12]以降低齿轮传递误差为优化目标对齿轮进行修形优化。齿轮传递过程中的载荷分布和传递误差都会影响齿轮的振动和噪声，因此齿轮修形需要同时兼顾齿轮载荷分布和传递误差。

笔者在前人研究的基础上，运用有限元法和切片理论建立斜齿轮啮合传递过程的动态接触模型，通过仿真分析指出对斜齿轮修形时单纯考虑以传递误差或者载荷分布均匀性为目标，很难获得最优修形参数组合方案。

1 斜齿轮传递误差激励分析

齿轮啮合传递的过程复杂，只有在绝对理想条件下才能实现传递过程的绝对平稳，而在实际工况中存在的轮齿弹性变形、载荷分布不均、制造和装配误差等因素都会影响齿轮传动的平稳性(称为“激励”)，进而产生冲击、振动和噪声。传递误差是衡量齿轮传动平稳性的重要指标。

1.1 问题的提出

在某款自动变速器的实验测试中发现，3挡工况下振动及噪声状况比较严重。通过阶次追踪法，可以判断引起振动和噪声的主要来源是其中一对斜齿轮，其结构尺寸参数如表1所示。

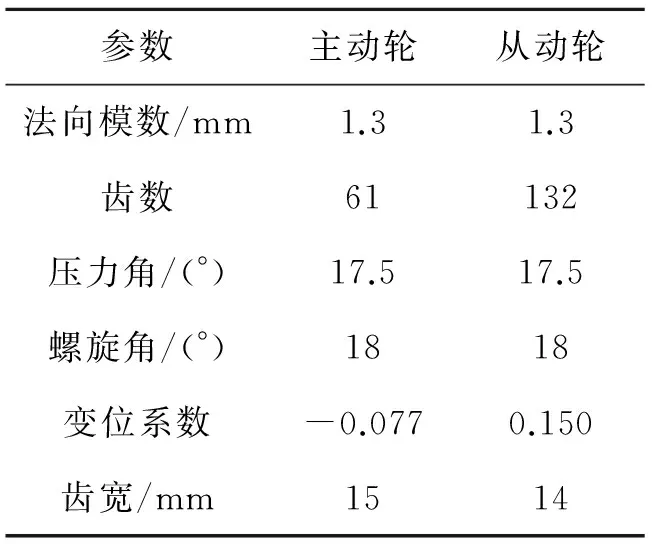
表1 斜齿轮的结构尺寸参数

1.2 有限元法

由于有限元法计算精度高，能适应各种复杂形状，已成为轮齿接触分析的工程分析有效手段。笔者采用弹性力学理论和有限元法分析轮齿动态啮合过程的接触特性。

在ANSYS仿真平台上建立有限元仿真模型，其中齿轮密度为ρ=7.8×10-6kg/mm3，弹性模量为E=2.1×105MPa，泊松比为λ=0.3。

由于在斜齿轮传动过程中，距离啮合轮齿较远的轮齿对整个斜齿轮传动几乎没有影响，因此为了提高计算效率，此处只建立包含啮合周期内的齿轮结构的三维有限元模型。单元类型选取为包含8个节点的SOLID185，每个节点有3个自由度。为了保证计算效率，在齿轮接触面区域需要对网格进行细化[13]，最终获得的有限元网格模型如图1所示。

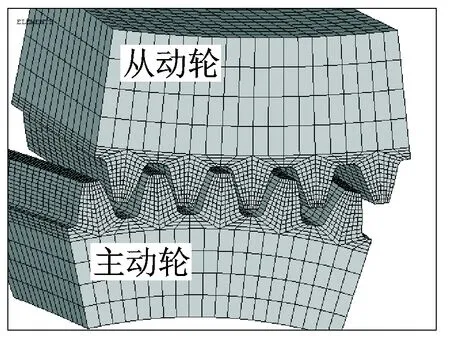
图1 齿轮啮合的有限元网格模型Fig.1 Finite element model of gear meshing

笔者研究的齿轮副的工况为主动轮输入转速为3 kr/min，输入扭矩为178 N·m。约束从动轮内圈表面节点所有的自由度，约束主动轮内圈表面节点除绕齿轮中心轴转动自由度外的所有自由度。并在主动轮内圈表面节点施加切向力以模拟转矩，切向力的计算公式[4]为

(1)

其中：T为施加扭矩；n为主动轮内圈表面节点数；r为主动轮内圈半径。

图2为由计算得到的主动轮应力云图，其中最大接触应力为987.5 MPa。文献[14]可计算出最大接触应力的理论值为963.2 MPa，显然两者的结果比较接近，说明该有限元模型是正确的，且可用于分析斜齿轮动态接触特性。

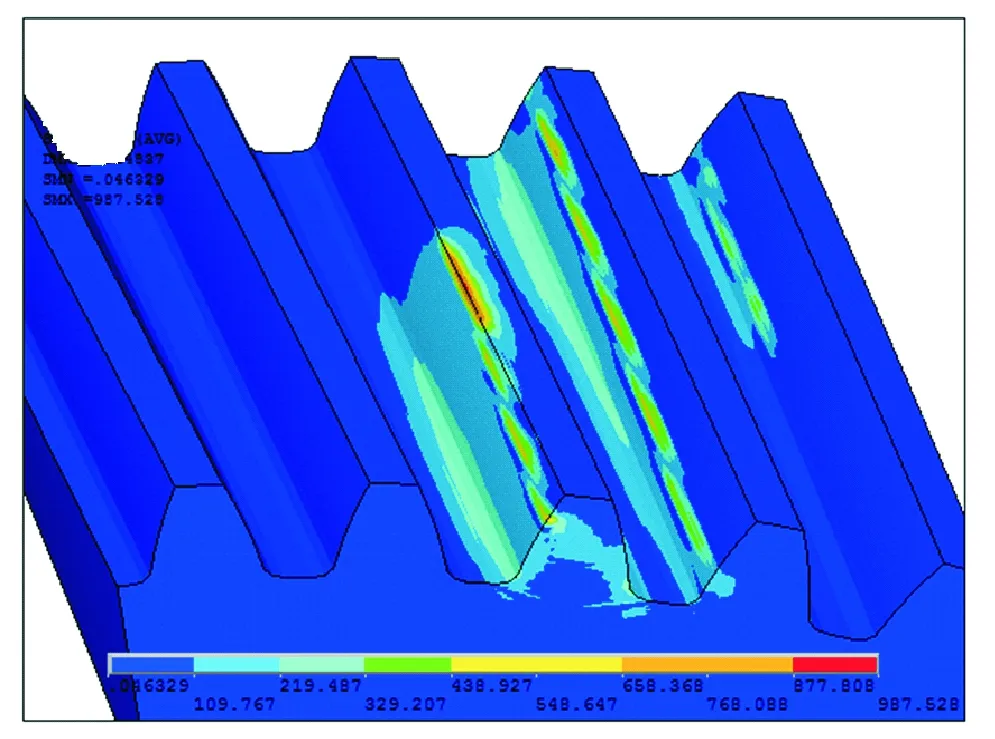
图2 主动轮所受应力云图Fig.2 Stress distributing graph of the driving gear

传递误差是衡量齿轮传动平稳性的重要指标，可表示[12]为

(2)

其中：E为轮齿综合偏差；δ为轮齿综合变形。

在一个啮合周期内，将主动轮和从动轮旋转的角度等距分成30份，重复上述求解过程，汇总主动轮和从动轮在每个求取位置沿啮合线方向的变形之和，并作为传递误差为纵坐标，从动轮相应转过的角度为横坐标，即可得到该斜齿轮的传递误差曲线，如图3所示，可以看出该斜齿轮的传递误差波动幅度为5.703 5 μm。图中波峰位置为3齿啮合，波谷位置为4齿啮合(文中的斜齿轮副重合度为3.325)，3齿啮合时的轮齿综合变形量要比4齿啮合时的更小。由于斜齿轮单双齿啮合的交替变化使得传递误差出现周期性变化。

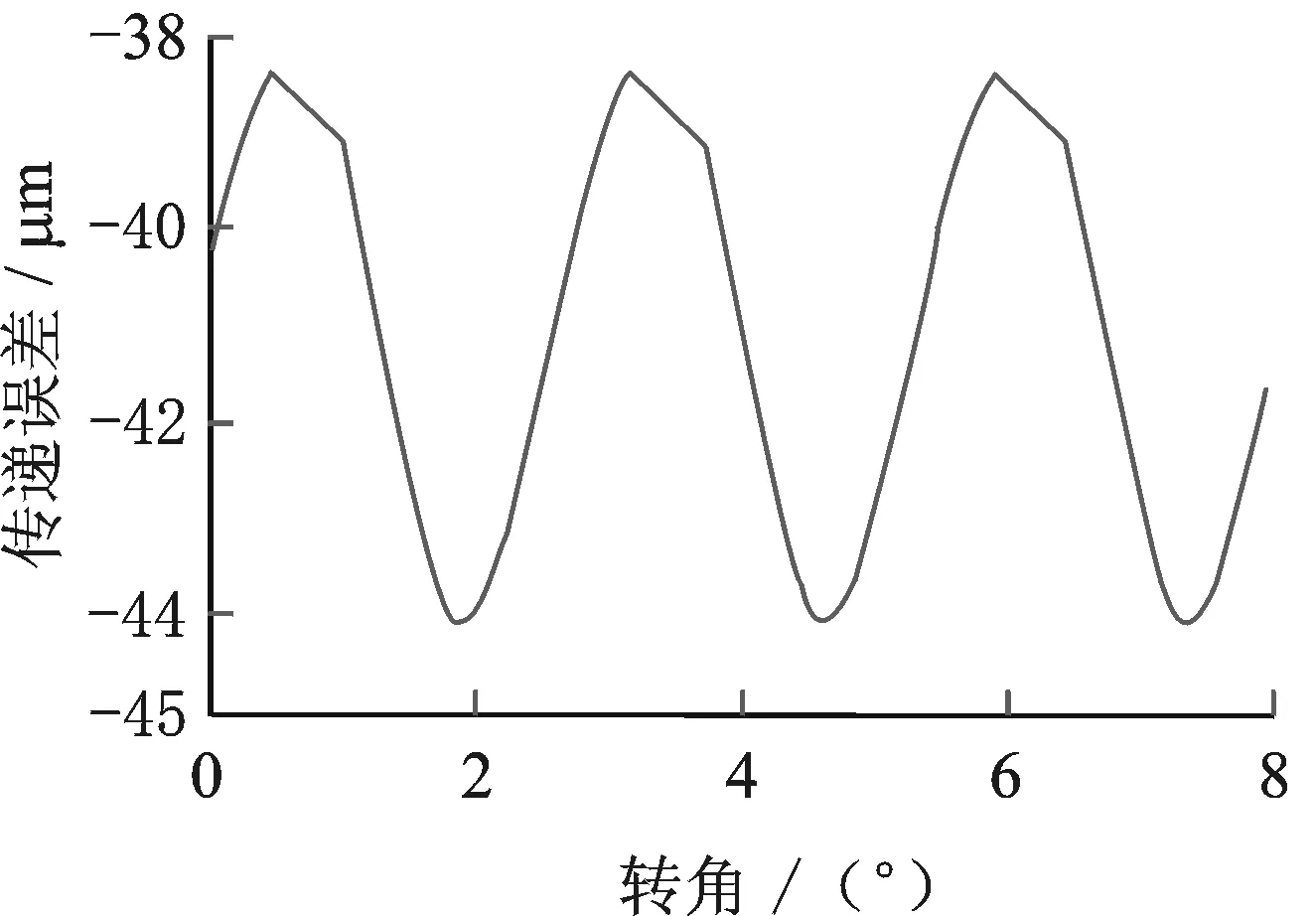
图3 斜齿轮传递误差Fig.3 Transmission error of helical gear

1.3 切片理论

采用有限元法可以得到齿轮受载时精确的接触变形量、接触刚度等，但有限元法计算时间一般较长，且难以精确考虑齿形误差、齿轮精度等因素的影响。

切片理论将齿轮沿齿宽方向等分为i份，则每个齿轮被切为多个切片，每个切片都被当做直齿轮，相邻的直齿轮是相互独立的。再对每个薄片沿齿廓方向等分为j份，则齿轮的齿面可以通过阵列i×j表示，阵列中每个元素都是具有一定刚度的弹簧。

阵列中每个元素的载荷计算[15]为

(3)

其中：Fs为切片刚度，其具体的取值根据单齿刚度和切片位置确定；TE为传递误差；x为齿形误差，其取值与齿轮齿面粗糙度和齿轮的精度有关。

根据切片理论，将笔者研究的齿轮副的齿面沿齿宽方向以单位长度1 mm长度等分，齿廓方向以单位长度0.5 mm等分，如图4所示。

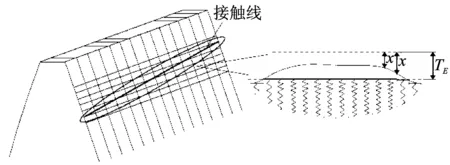
图4 斜齿轮切片模型Fig.4 Thin slice model of helical gear

图5(a)为根据切片理论基于Romax仿真平台计算得到的斜齿轮的传递误差。显然，采用切片理论法得到斜齿轮的传递误差波动幅值为5.059 6 μm，与有限元法得到的结果非常接近。传递误差曲线的周期为2.73 deg，在一个啮合周期中其中三齿啮合区域为0～1.84 deg，四齿啮合区域为1.84～2.73 deg。同时传递误差曲线也明显出现周期性变化。

图5(b)为齿轮齿面载荷分布情况，从图中可以看出齿面上最大单位长度载荷为196.7 N/mm，载荷分布不均匀，主要分布在齿面的左侧。

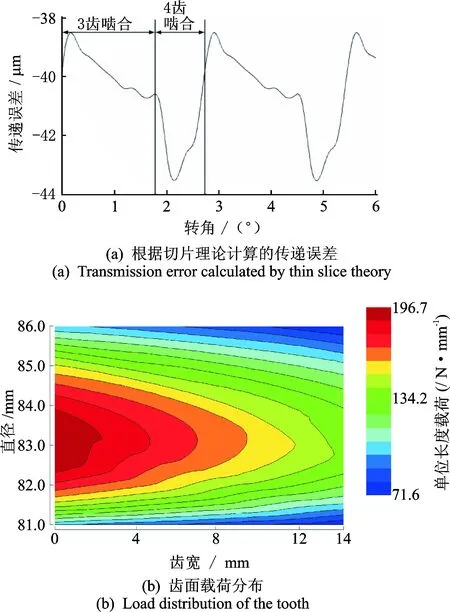
图5 根据切片理论计算的结果Fig.5 Results calculated by slice theory

斜齿轮的传递误差波动和载荷分布不均都会成为产生振动和噪声的激励源，通过降低斜齿轮的传递误差波动和改善斜齿轮载荷分布可以降低齿轮的振动和噪声，而通过齿轮修形可以降低斜齿轮传递误差并改善齿面载荷分布。

2 斜齿轮修形参数优化

齿轮修形是目前齿轮减振降噪的主要方法。常用的齿轮修形包括齿廓修形和齿向修形，前者可以减小斜齿轮的啮合冲击、降低传递误差波动，后者可以降低传递误差波动、改善齿轮载荷分布。本研究选取齿廓的修形量、修形高度和鼓形修形量作为优化的齿轮修形参数。

在齿廓修形方面，根据推荐公式，可计算出该斜齿轮的修形参数为：最大修形量Δmax=0.02mn=0.026 mm；最大修形高度hmax=0.65mn=0.845 mm，其中mn为齿轮法向模数。

在齿向修形方面，鼓形修形公式[16]为

(4)

其中：C为啮合综合刚度；b为齿宽；bcal为有效接触齿宽；Fm为圆周力；Fβy为啮合齿向误差。

根据机械设计手册可求得各个参数值分别为：C=11.256 GPa，b=14 mm，bcal=26.641 mm，Fm=6 961.3 N，Fβy=2.311 3 μm。根据斜齿轮参数计算可得,Ca=23.8 μm。

大量仿真发现，齿廓修形中采用直线修形和抛物线修形的结果很接近[5]。考虑到抛物线修形的加工成本要高得多，故齿廓修形采用直线修形，齿轮修形参数范围如表2所示。

表2 斜齿轮副修形参数

根据切片理论模型，在斜齿轮修形参数范围内，采用列举法，齿顶修形宽度、齿根修形宽度和齿向鼓形量以0.01 μm为步长选取修形参数；齿顶和齿根修形高度以1 μm为步长选取修形参数。

2.1 以传递误差波动最小为修形目标

斜齿轮在传递扭矩过程中，受到轮齿变形和齿轮误差的影响使得斜齿轮的传递误差是波动的，传递误差的波动会作为一种动态激励导致齿轮受载时产生的作用力波动，从而产生振动引起噪声。因此,降低斜齿轮传递误差波动可以降低斜齿轮的振动和噪声。

以斜齿轮的传递误差波动最小为目标，通过比较所有仿真结果，获得一组最佳修形参数，如表3所示。其对应的传递误差和载荷分布如图6所示。

表3 以传递误差波动最小为目标修形参数

Tab. 3 Modification parameters of minimum transmission error

齿轮Δ1/μmh1/mmΔ2/μmh2/mmCa/μm主动轮2.300.6022.300.5980.70从动轮3.400.6023.400.5980.67

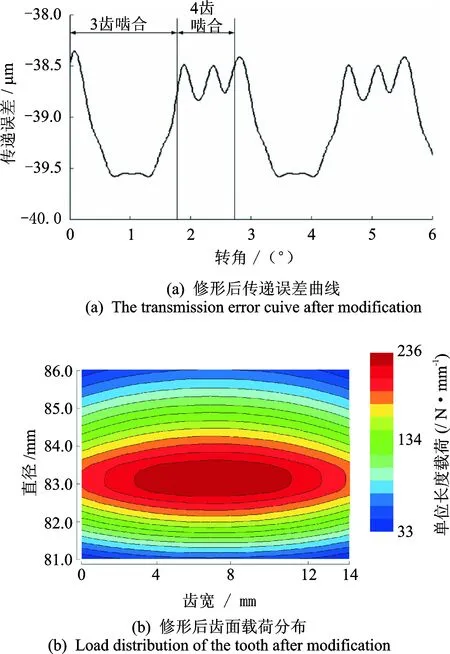
图6 以传递误差波动最小为目标修形后的结果Fig.6 Results of minimum transmission error as target

从图6(a)中可以看出，修形后斜齿轮传递误差的波动为1.225 3 μm，比修形前降低了75.78%，但波峰处曲线变化剧烈说明有冲击产生。从图6(b)中可以看出，修形前齿面的载荷分布不均匀，而修形后的齿面载荷分布则转移到以齿面中间区域为中心均匀散开，但是其对应的单位长度载荷却提高到236 N/mm，相比修形前增加了19.98%。说明单纯考虑最小传递误差波动进行齿轮修形无法获得最优修形参数组合方案。

2.2 以斜齿轮载荷分布最优为修形目标

修形前的齿面载荷分布不均匀，这会引起斜齿轮传动过程中出现偏载，使得传动不平稳，造成振动和噪声。以齿宽方向载荷分布均匀，齿廓方向中间载荷大，齿顶、齿根载荷小为修形目标，对斜齿轮修形优化。通过比较所有仿真结果，获得一组最优的修形参数方案，如表4所示，其对应的载荷分布和传递误差如图7所示。

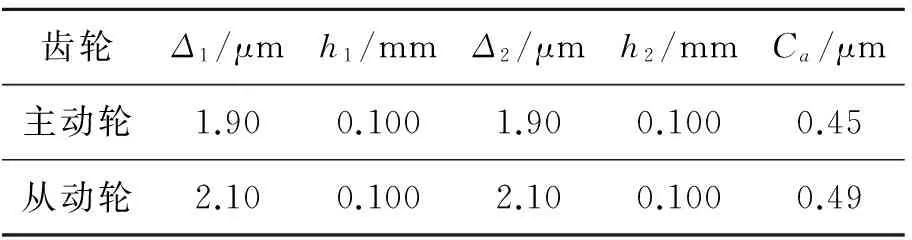
表4 以斜齿轮载荷分布最优为目标修形参数

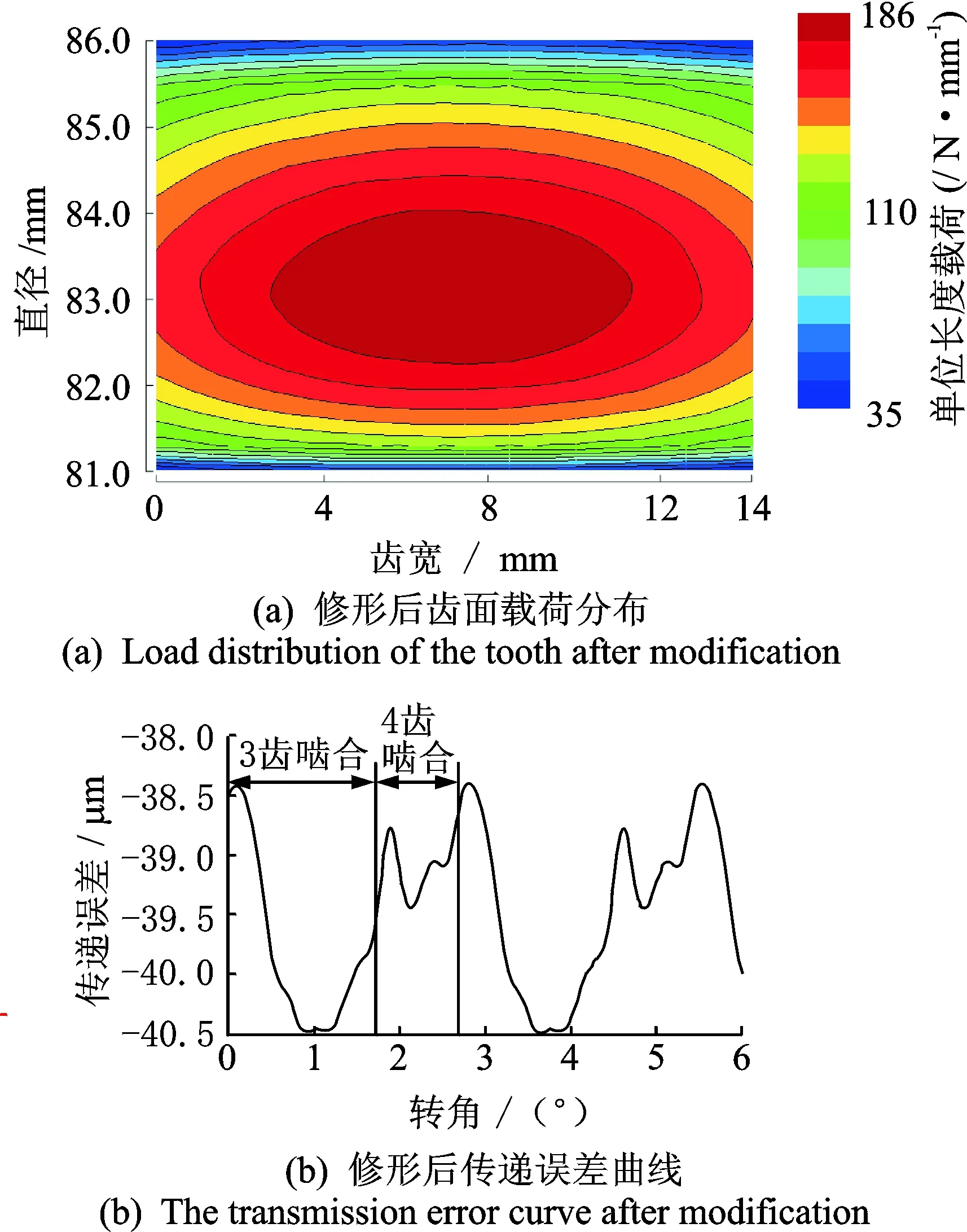
图7 以载荷分布最优为目标的修形结果Fig.7 Modification result of optimal load distribution

由图7与修形前结果对比可以看出，修形后的齿面载荷分布非常均匀，而且单位长度载荷最大值得到了有效的降低。但是，修形后的传递误差波动幅值却为2.077 9 μm，虽然比修形前降低了近60%，但比以传递误差最小为目标的优化方案对应值增大了近63.9%。修形后的传递误差曲线波峰处发生较大的波动，说明有一定的冲击产生。显然，单纯考虑载荷分布最优进行齿轮修形也无法获得最优的修形参数组合方案。

2.3 综合考虑传递误差和载荷分布的修形

上述分析表明，对斜齿轮进行修形时需要同时考虑其传递误差和载荷分布才能获得最优修形参数组合方案。综合考虑斜齿轮传递误差和载荷分布，通过比较所有仿真结果，获得一组最优修形参数方案，如表5所示，其对应的传递误差和载荷分布如图8所示。

表5 综合考虑传递误差和载荷分布的修形参数

Tab. 5 Modification parameters considering transmission error and load distribution

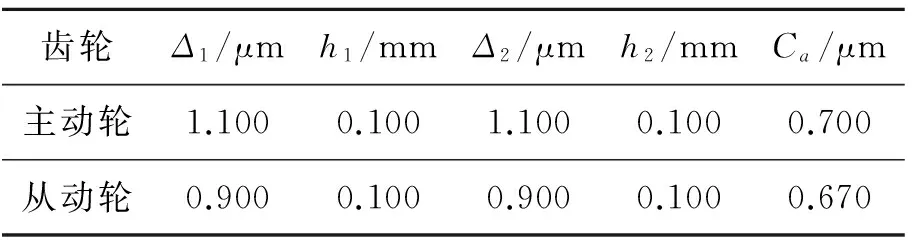
齿轮Δ1/μmh1/mmΔ2/μmh2/mmCa/μm主动轮1.1000.1001.1000.1000.700从动轮0.9000.1000.9000.1000.670

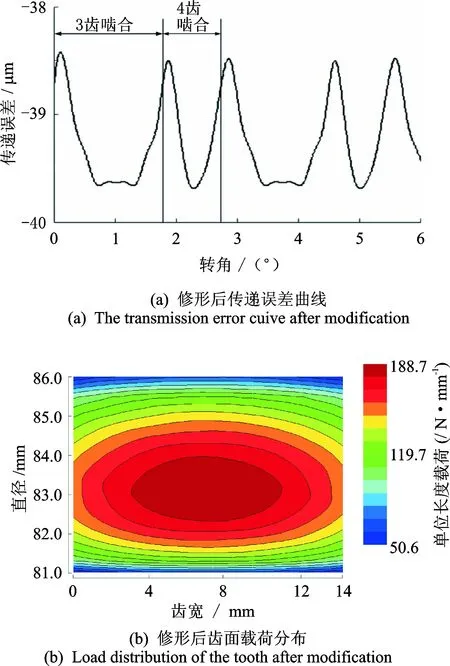
图8 综合考虑传递误差和载荷分布修形后的结果Fig.8 Results after modification considering transmission error and load distribution

从图8(a)中看出，修形后的斜齿轮传递误差波动为1.277 1 μm，比修形前降低了74.76%，且比以传递误差波动最小为优化目标的方案仅提高了4%；从传递误差曲线中可以看出，在一个啮合周期中，曲线出现两次波峰到波谷的变化，其中一个从波峰到波谷的变化为4齿啮合时产生的冲击，另一个从波峰到波谷的变化为3齿啮合时产生的冲击；虽然斜齿轮啮合过程中都有一定的冲击，但由于传递误差的波动要比修形前小得多，所以修形后的斜齿轮传动要比修形前好得多。从图8(b)中看出，修形后齿面的载荷分布均匀，主要介于齿顶与齿根之间；且最大单位长度载荷相比修形前得到了有效的降低。该修形方案确定为最佳修形方案。

3种不同修形方案的结果如表6所示。

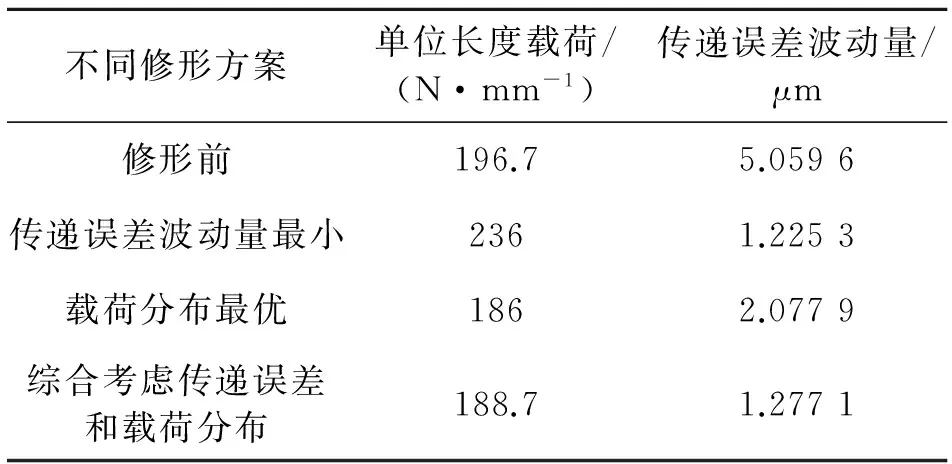
表6 3种不同修形方案结果

3 实验验证

为了进一步分析本研究修形方案的减振降噪效果，对装配该齿轮的自动变速器进行振动和噪声实验分析，其中测试的输入扭矩为178 N·m，输入转速从0 r/min增加到5 000 r/min。传感器布置如图9所示。其中：M1和M2分别为麦克风1和2；Tacho为测速器；V_x，V_y，V_z为三轴加速度传感器的布置形式，方向分别为整车+x,+y,+z方向，总计两个三向传感器；V_diff为单轴加速度传感器。通过台架试验得到变速器总噪声测试结果如图10(a)所示，通过噪声切片分析得到斜齿轮噪声如图10(b)所示。

图9 实验原理图Fig.9 Actual experimental apparatus

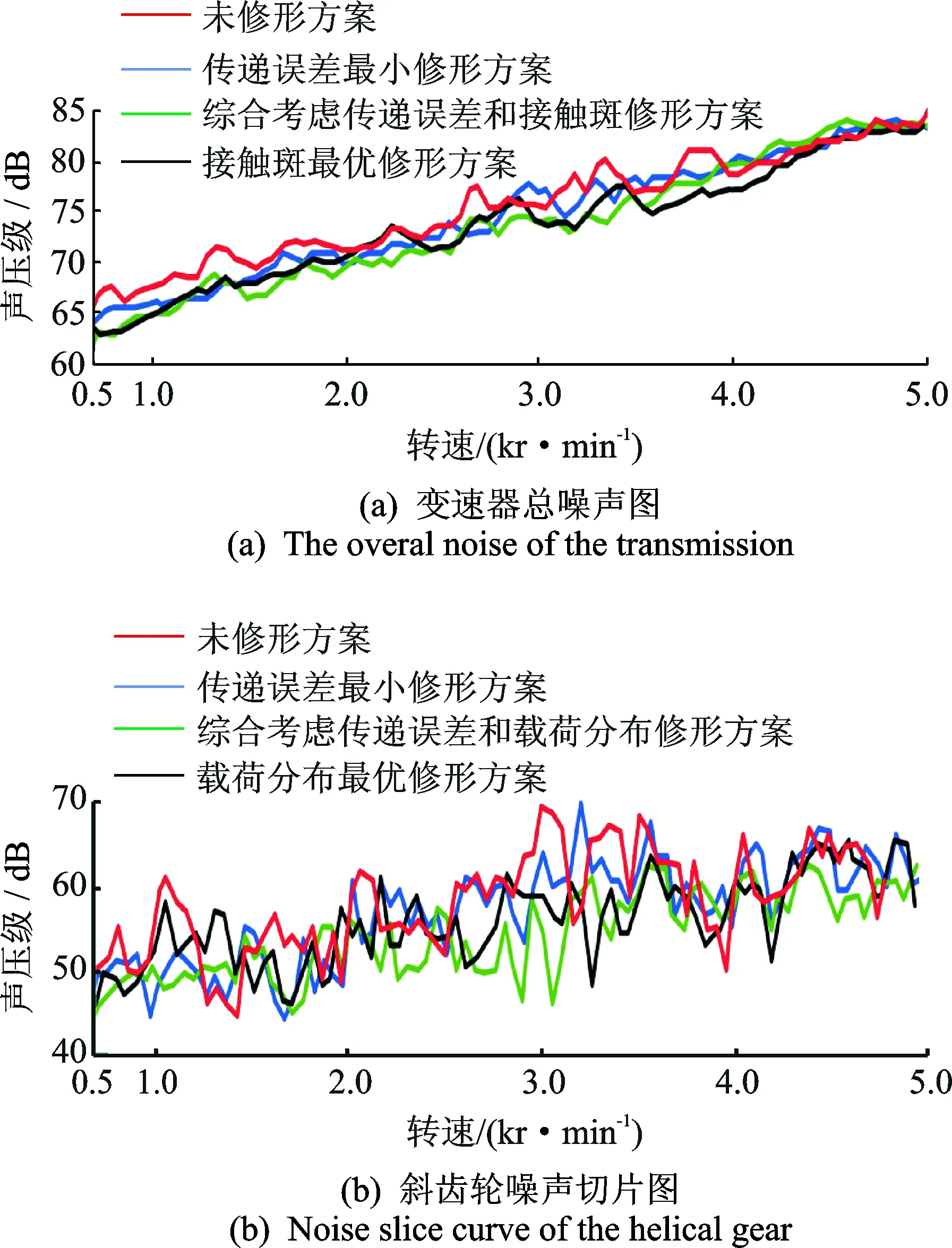
图10 修形前后噪声对比Fig.10 Noise compared with before and after modification

从图10(a)中可以看出，三种修形方案都可以降低斜变速器的噪声，降低约0～4 dB；且输入转速在1 500～3 500 r/min范围内时，综合考虑传递误差和载荷分布的修形方案降噪效果最好。从图10(b)中可以看出，当输入转速在2 700～3 200 r/min范围内时，三种修形方案都有较好的减振降噪效果，且综合考虑传递误差和载荷分布的修形方案的斜齿轮降噪效果最好，这与本研究的工况很接近，说明本研究的修形方案是正确合理的。

4 结 论

1) 采用有限元法和切片理论分析了斜齿轮啮合传递过程，衡量斜齿轮啮合传动的平稳性，通过对传递误差仿真结果的相互验证，证明两种方法及其模型的有效性。

2) 仅单一考虑斜齿轮的传递误差或者齿面载荷分布情况对斜齿轮修形均无法得到最优的修形方案，斜齿轮修形需综合考虑斜齿轮传递误差和齿面载荷分布情况。

3) 自动变速器噪声实验测试结果证实，同时兼顾接触斑和传递误差的修形方法可以更有效地降低齿轮噪声，且有利于保证齿轮的可靠性运转。

[1] 王彦刚，郑海起，杨通强，等．故障参数下齿轮系统非线性动力学行为[J]．振动、测试与诊断，2011，31(5)：570-573．

Wang Yangang，Zheng Haiqi，Yang Tongqiang，et al. Nonlinear dynamics behavior of gear system with fault parameters[J]．Journal of Vibration，Measurement & Diagnosis，2011，31(5)：570-573．(in Chinese)

[2] Peeters J L M，Dirk V，Paul S．Analysis of internal drive train dynamics in a wind turbine[J]．Wind Energy，2006，9(1)：141-161．

[3] Harris S L．Dynamic loads on the teeth of spur gears[J]．Proceedings of Institution of Mechanical Engineers，1958，172(1)：87-112．

[4] 张义民，杨健，胡鹏．斜齿轮副传递有限元误差分析[J]．机械设计与制造，2014，3(3)：189-191．

Zhang Yiming，Yang Jiang，Hu Peng．Helical gears transmission error of finite element analysis[J]．Machinery Design and Manufacture， 2014，3(3)：189-191．(in Chinese)

[5] 袁哲．齿轮振动可靠性与修形减振策略研究[D]．沈阳：东北大学，2010．

[6] 马辉，王奇斌，黄婧，等．不同自由度耦合斜齿轮转子系统的振动特性[J]．振动、测试与诊断，2014，34(4)：650-657.

Ma Hui，Wang Qibin，Huang Jing，et al．Vibration characteristics analysis of a helical gear rotor system considering different degrees of freedom coupling[J]．Journal of Vibration，Measurement & Diagnosis，2014，34(4)：650-657．(in Chinese)

[7] 胡鹏，张义民，王倩倩．含侧隙及时变刚度的多级齿轮非线性响应分析[J]．振动、测试与诊断，2013，33(S1)：115-119．

Hu Peng，Zhang Yimin，Wang Qianqian．Nonlinear dynamic analysis of spur gear pairs with gear backlash and time-varying stiffness[J]．Journal of Vibration，Measurement & Diagnosis，20113，33(S1)：115-119．(in Chinese)

[8] 吴勇军，王建军，韩勤锴，等．基于接触有限元分析的斜齿轮齿廓修形与实验[J]．航空动力学报，2011，26(2)：409-415．

Wu Yongjun，Wang Jianjun，Han Qinkai，et al．Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J]．Journal of Aerospace Power，2011，26(2)：409-415．(in Chinese)

[9] Conry T F，Seireg A．A mathematical programming technique for the evaluation of load distrbution and optimal modifications for gear systems[J]．Journal of Engineering for Industry，1973，95(4)：1115-1122．

[10]尚振国，王华．宽斜齿轮修形有限元分析[J]．农业机械学报，2009，40(2)：214-219．

Shang Zhenguo，Wang Hua．Finite element analysis of modified wide helical gears[J]．Transactions of the Chinese Society for Agricultural Machinery，2009，40(2)：214-219．(in Chinese)

[11]Tavakoli M S，Houser D R．Optimum profile modificaitons for the minimization of static transmission errors of spur gears[J]．Journal of Mechanisms，Transmissions，and Automation in Design，1986，108(1)：86-94．

[12]Bonori G，Barbieri M，Pellicano F．Optimum profile modifications of spur gears by means of genetic algorithms[J]．Journal of Sound and Vibration，2008，313(3-5)：603-616．

[13]张建宇，刘鑫博，张飞斌．裂纹齿轮啮合刚度的劣化特性[J]．振动、测试与诊断，2014，34(6)：1124-1128．

Zhang Jianyu，Liu Xinbo，Zhang Feibin．Degradation characteristics of meshing stiffness of spur gears with root crack[J]．Journal of Vibration，Measurement & Diagnosis，2014，34(6)：1124-1128．(in Chinese)

[14]王之栎，马纲，陈心颐．机械设计[M]．北京：北京航空航天大学出版社，2011：74-75．

[15]张靖．不同因素激励下齿轮传动系统动力学仿真及实验研究[D]．重庆：重庆大学，2012．

[16]李润方．齿轮传动的刚度分析和修形方法[M]．重庆：重庆大学出版社，1998：243-249．

10.16450/j.cnki.issn.1004-6801.2016.05.022

国家自然科学基金资助项目(51405010)；航空科学基金资助项目(2015ZA51003)

2015-05-08；

2015-08-14

TH132.413; U463.212

刘艳芳，女，1978年8月生，博士、讲师。主要研究方向为机械传动，齿轮的振动与噪声。曾发表《Study on vibration characteristics and tooth profile modification of a plusplanetary gear set》(《Journal of Vibroengineering》2014,Vol.16,No.1)等论文。

E-mail:laijunbin5@163.com