基于柔性铰链的柔性放大机构参数化设计
卢 倩, 黄卫清, 孙梦馨
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
基于柔性铰链的柔性放大机构参数化设计
卢 倩, 黄卫清, 孙梦馨
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
为了对柔性微位移放大机构进行优化设计,有必要对柔性铰链及柔性放大机构进行参数化分析与研究。提出了一个通用的结构参数ε,探讨了ε对不同柔性铰链柔度系数的影响规律,并横向比较了常用柔性铰链的柔度特性。另一方面,基于柔度特性的影响分析,提出了新的参数柔度比λ,重点分析了不同柔度比λ的柔性铰链主要输出位移形式的灵敏度。以实际的桥式柔性微位移放大机构为例,利用参数ε和λ实现了该柔性放大机构的参数化设计,并用有限元软件进行了仿真计算。实验测量结果表明,对基于柔性铰链的柔性微位移放大机构进行参数化设计,最终输出位移行程与有限元仿真设计的结果误差率为3.80%。基于柔性铰链的结构参数ε和柔度比λ对柔性放大机构进行参数化设计是可行且正确的,有利于这一类柔性放大机构的优化设计。
柔性铰链; 柔性放大机构; 结构参数; 柔度比; 参数化设计
引 言
随着光纤通信技术的发展,光学定位调整平台正朝着高精度、大行程的方向发展,但光学定位平台的行程扩增会导致误差累积,这对系统定位精度构成威胁[1]。如何实现高精度与大行程之间的平衡,是光学精密定位仪器发展的瓶颈。柔性铰链以其无机械摩擦、无间隙及运动灵敏度高等优点成为光学精密定位平台及仪器的首选,但由于柔性铰链的微位移是利用自身结构薄弱部分的微小弹性变形及其自回复特性而实现的,其范围一般在几微米到几十微米之间[2],因此必须借助于微位移放大机构来实现柔性铰链机构输出的微位移的放大和传递,以满足光学定位工作台的行程要求。
目前常用的微位移放大机构主要有多级杠杆放大机构[3-4]、差动杠杆放大机构[5]、三角放大机构[6]和桥式放大机构[7-8]等。杠杆放大机构原理简单,易于实现,理论上能够实现输出对输入的线性放大,但是杠杆机构的放大增益有限,采用多级杠杆机构又容易引起误差累积和体积过大等问题[9]。差动式杠杆放大机构能够提高放大比,但仍无法实现较为紧凑的结构,同时差动杠杆式放大机构的分析较为复杂,限制了其进一步应用的范围。利用三角放大原理设计的桥式放大机构具有结构紧凑、分析简单和位移放大增益较大等优点。因此,桥式放大机构近几年得到了广泛研究与应用。
结构柔度直接影响到柔性微位移放大机构的整体性能,很多学者采用不同的建模方法对柔性机构的结构柔度与放大性能进行了研究[10-14],但基本都是遵循着“给定结构尺寸-柔度分析-优化设计”的思路,且并没有给出放大增益比的计算方法。事实上,位移放大增益是体现和反映柔性微位移放大机构性能优劣的决定性指标,且与柔性机构的结构柔度息息相关。宫金良等[15]提出了一种基于刚度目标的微位移放大模块闭环设计方法。沈剑英等[16]在考虑柔性铰链转动中心偏移量的基础上推导了多级杠杆式柔性铰链机构放大率计算公式。李威等[17]采用矩阵法计算推导了基于平行四杆机构的柔性桥式微位移放大机构的输出位移及位移放大比。Bolzmacher等[18]设计了一种多级杠杆式位移放大机构,利用有限元分析方法对放大机构的放大比性能进行了仿真分析。Ma等[19]对桥式微位移放大机构的柔度与位移计算公式进行了推导和简化,并采用弹性梁理论探讨了桥式放大机构的位移放大比特性。Xu等[20]设计了一种桥式位移放大器,并采用欧拉-伯努利梁理论分析了其位移放大比特性。Choi等[21]利用压电叠堆元件设计了一种新型桥式放大机构,实现了位移和机械力的双向放大,并给出了放大机构的柔度和输出位移的计算方法。在上述的研究中,或集中讨论某一类特定类型的柔性铰链柔度模型,或设计特定结构形式的柔性微位移放大机构,或采用静力学、动力学等方法研究特定结构类型的位移放大机构的性能;普遍缺乏对柔性放大机构的参数化分析,缺乏对柔性微位移放大机构的参数化设计研究,而结构参数对柔性微位移放大机构的放大增益以及其末端运动精度具有决定性作用[22],但目前在这方面的研究并不多。因此,有必要开展面向柔性微位移放大机构的参数化设计研究。
本研究课题拟提出一个通用的结构参数ε,并探讨结构参数ε对柔性铰链的柔度系数的影响,从而实现利用该参数将4种常用的柔性铰链的柔度特性进行横向对比。基于结构参数ε的变化对于常用柔性铰链的柔度特性的影响规律,提出柔度比λ的概念,重点分析不同柔性铰链主要输出位移形式的灵敏度,并结合实际的柔性桥式微位移放大机构,利用参数ε和λ实现对桥式柔性放大机构的参数化设计,并用有限元仿真方法和实验验证该参数化设计的可行性与正确性。
1 柔性铰链参数化分析
1.1 结构参数ε
1) 参数ε的定义
考虑到柔性铰链的易于加工性及其运动性能,目前研究和应用较多的柔性铰链主要有4种:直梁型、倒圆角直梁型、直圆型和椭圆型柔性铰链,分别如图1(a)~(d)所示。直圆型铰链切口半径为R1,倒圆角直梁型铰链的圆角半径为R2,直梁型铰链切口直梁长度为2L1,倒圆角直梁型铰链的直梁部分长度为2L2,椭圆柔性铰链的长轴半径和短轴半径分别为a和b(a≥b),所有铰链的宽度均为w,最小切割厚度均为t。
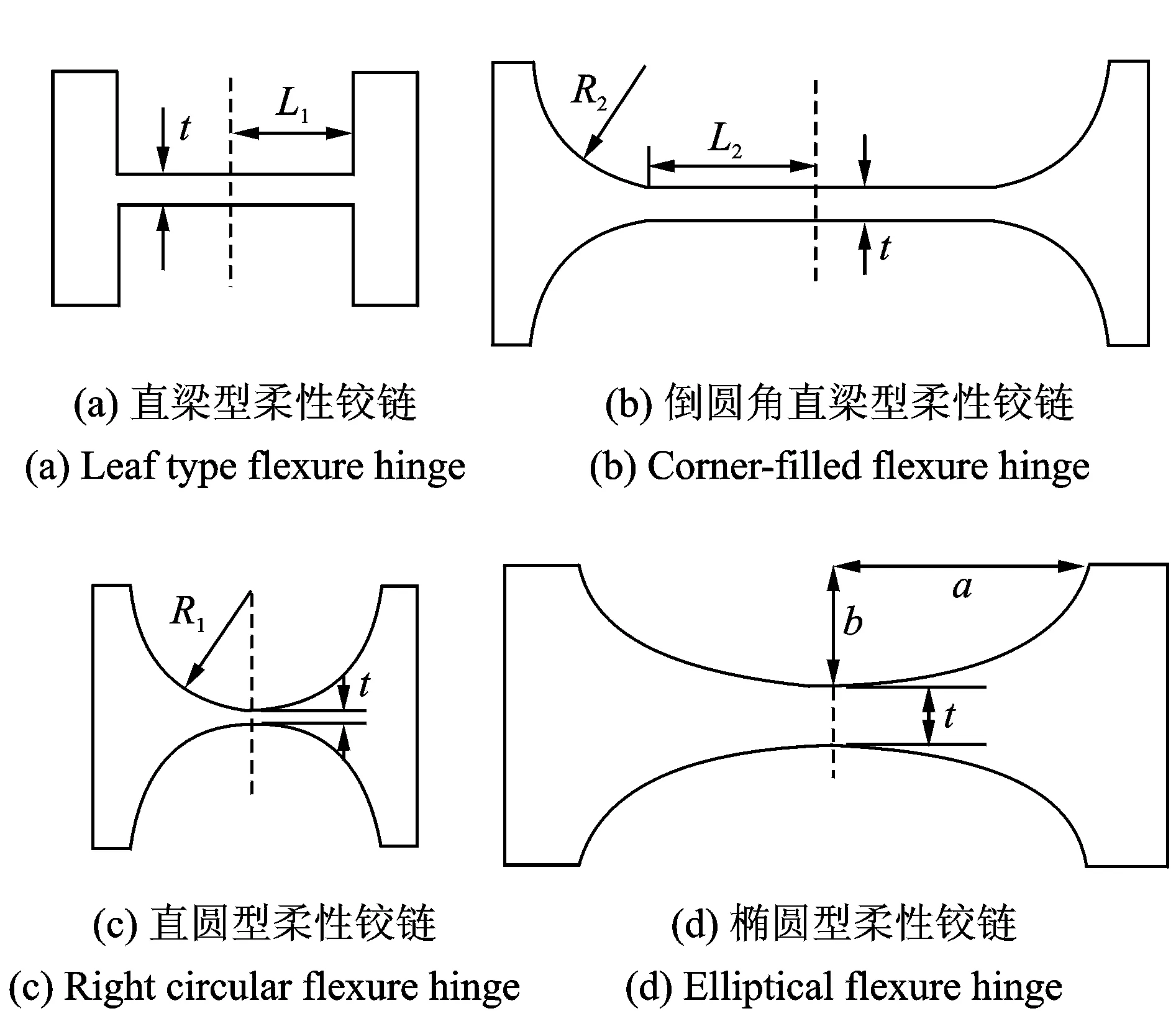
图1 4种常用的柔性铰链Fig.1 Four common flexure hinges
柔度模型对于柔性铰链的运动能力和运动性能影响至关重要,其研究结论也比较成熟,但是目前并没有一个统一的结构参数,能够将上述四种柔性铰链的柔度模型进行纵向比较。于志远等[23]提出了利用铰链切口处长宽之比作为铰链形状参数,但是该参数只能够体现铰链切口的不同形状对柔性铰链柔度的影响,并没有实现真正意义上的结构参数对铰链柔度的影响分析。
考虑到四种柔性铰链的最小切割厚度t对其柔度模型的影响都最为敏感[24-25],本研究课题提出一个统一的结构参数ε,令其为柔性铰链的切口长度一半与最小切割厚度之比,即
(1)
其中:lx为柔性铰链的切口长度。
结合图1有:
对于直梁型柔性铰链,lx1=2L1,ε1=L1/t;
对于倒圆角直梁型柔性铰链,lx2=2(L2+R2),ε2=(L2+R2)/t;
对于直圆型柔性铰链,lx3=2R1,ε3=R1/t;
对于椭圆型柔性铰链,lx4=2a,ε4=a/t。
2) 参数ε对柔性铰链结构柔度的影响
柔性铰链工作时,其转动柔度Cαz和拉伸柔度CΔx直接决定着铰链绕Z轴转动的角位移αz和沿X轴产生的拉伸线位移Δx,这也是衡量柔性铰链精度和性能的主要指标。上述四种柔性铰链柔度模型的影响因素中,按照影响程度从大到小的顺序,都是最小切割厚度t,切口长度lx,宽度w[24-25]。为此,重点考察最小切割厚度t变化时,结构参数ε对柔性铰链的转动柔度Cαz和拉伸柔度CΔx的影响变化关系。
假定柔性铰链一端固定,另一端自由,仅受轴向力Fx和弯矩Mz的作用。令柔性铰链的切口长度lx不变,改变最小切割厚度t。参数给定如下:Fx=10 N;Mz=1 N·m;L1=5 mm;L2=4mm;R2=1 mm;R1=5 mm;a=5 mm;b=3 mm;w=8 mm;材料弹性模量E=2.1×1011N·m-2。结合文献[24-25]中对常用柔性铰链柔度模型的结论,编写Matlab数值仿真程序,其柔度计算结果如图2所示。
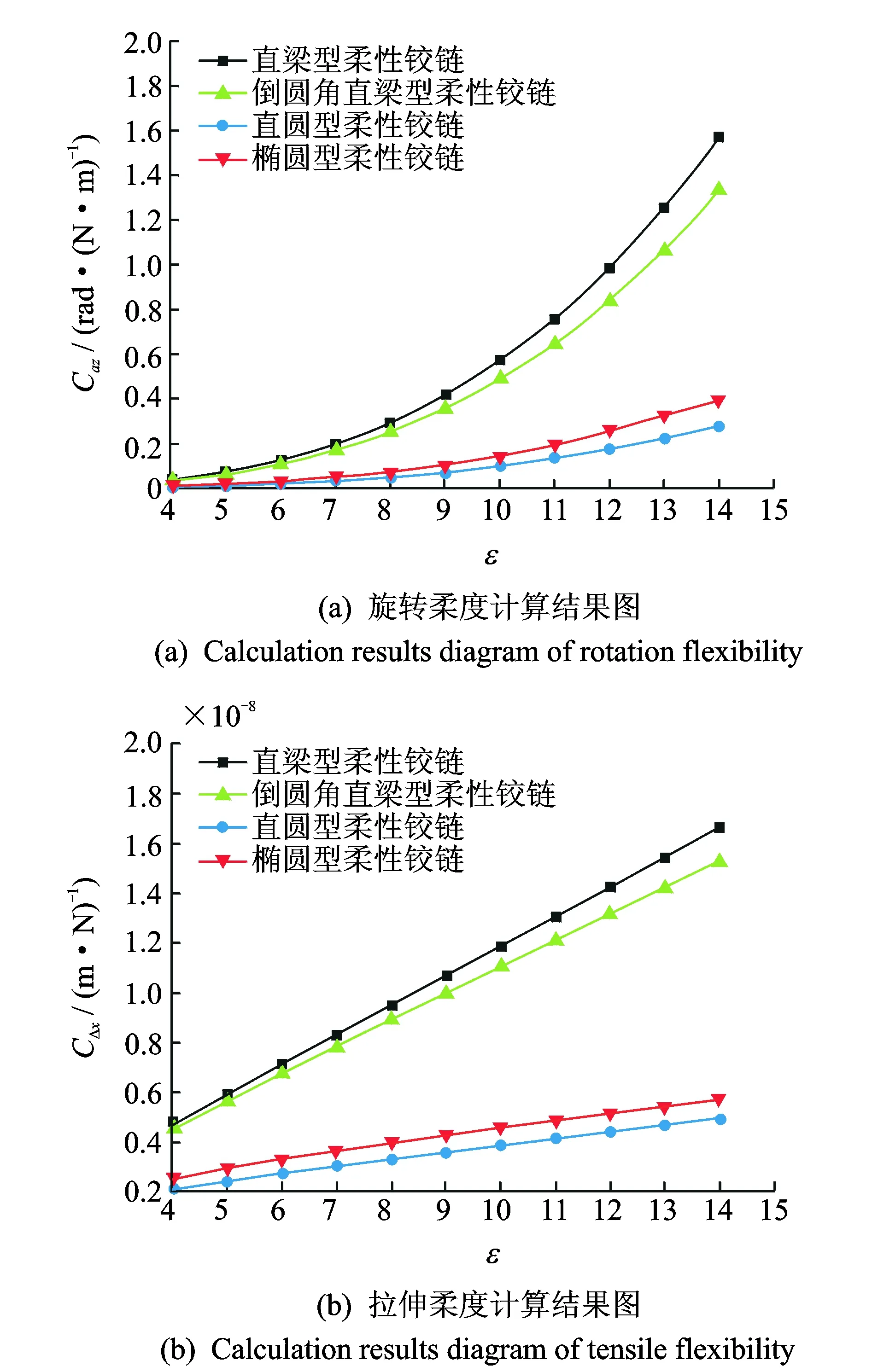
图2 t变化时ε对柔性铰链柔度的影响关系Fig.2 Relationship between ε and flexibility of flexure hinges with varied t
当铰链的的切口长度lx不变、最小切割厚度t变化时,4种柔性铰链的旋转柔度和拉伸柔度的计算结果分别如图2(a),(b)所示。直圆型和椭圆型柔性铰链的旋转柔度及拉伸柔度均明显小于直梁型和倒圆角直梁型柔性铰链的旋转柔度及拉伸柔度。随着结构参数ε的变大,4种柔性铰链的转动柔度和拉伸柔度都在逐渐增大,这表明,当柔性铰链的切口长度lx一定时,随着铰链最小切割厚度t的减小(ε逐渐变大),4种柔性铰链的转动柔度和拉伸柔度都逐渐变大,故在相同外力或外力矩的作用下,铰链绕Z轴的转动角位移αz和沿X轴的轴向线位移Δx都会变大。因此,当柔性铰链的切口长度lx一定时,减小最小切割厚度t可以有效提高铰链的工作行程范围。
观察图2还可以发现,在相同规格尺寸条件下,直梁型柔性铰链的转动柔度和拉伸柔度都是最大的,直圆型柔性铰链的转动柔度和拉伸柔度都是最小的,这表明,偏转相同的角度αz或者产生相同的轴向线位移Δx,直梁型柔性铰链所需的弯矩或轴向力是最小的,因而适合小力矩驱动场合;直圆型柔性铰链所需的弯矩或轴向力是最大的,因而适合大力矩驱动场合;在相同弯矩或轴向力的作用下,相对而言,直圆型柔性铰链的转动角位移αz或轴向线位移Δx是最小的,适合工作行程范围较小的场合;而直梁型柔性铰链的转动角位移αz或轴向线位移Δx是最大的,因而适合于工作行程范围较大的场合。
1.2 柔度参数λ
1) 参数λ的定义
柔性微位移放大机构是利用自身结构实现对柔性铰链的微小位移进行放大和传递,但柔性铰链往往同时受到轴向力Fx和弯矩Mz的作用,会同时产生轴向线位移和旋转角位移,最终会对柔性微位移放大机构的执行末端的定位精度及整体位移放大性能产生影响。为此,需要讨论柔性铰链在同时受到轴向力Fx和弯矩Mz的作用时,其主要输出位移形式的灵敏度。
定义柔度比λ为
(2)
柔度比λ越大,表明该柔性铰链相对而言越容易产生拉伸轴向线位移,越不容易产生旋转角位移。实际上,柔度比λ反映的是柔性铰链在受轴向力Fx和弯矩Mz同时作用时,柔性铰链主要输出位移形式的灵敏度,也就是说,柔度比λ越大,则该柔性铰链的主要输出位移形式为轴向线位移的灵敏度越高,即越容易产生轴向线位移;反之,则柔性铰链主要输出旋转角位移的灵敏度越高,即越容易产生旋转角位移。
2) 参数λ-ε的关系
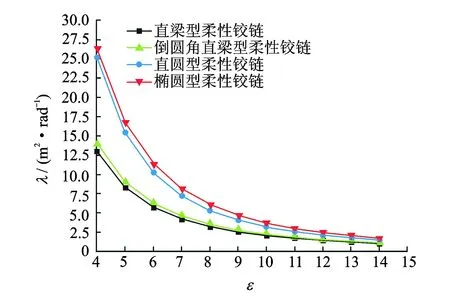
图3 柔度比λ随ε的变化关系Fig.3 Relationship between flexibility ratio λ and ε
沿用上述柔性铰链的相关结构参数,编写Matlab数值仿真程序,柔度比λ随结构参数ε的变化关系如图3所示。随着结构参数ε的变大,4种柔性铰链的柔度比λ都在逐渐减小,这表明,当柔性铰链的切口长度lx一定时,随着铰链最小切割厚度t的减小(ε逐渐变大),4种柔性铰链的主要输出位移形式中,轴向线位移的输出灵敏度逐渐降低,而旋转角位移的输出灵敏度逐渐提高。即,随着结构参数ε的变大,4种柔性铰链的主要输出位移形式逐渐由轴向线位移向旋转角位移过渡。
从图3还可以发现,直梁型和倒圆角直梁型柔性铰链的柔度比λ明显小于直圆型和椭圆形柔性铰链的柔度比λ,这说明当柔性铰链同时受到轴向力Fx和弯矩Mz作用时,直梁型和倒圆角直梁型柔性铰链相对另两种铰链,其输出位移的主要形式是旋转角位移;而直圆型和椭圆形柔性铰链相对另外两种铰链更容易产生轴向线位移。这对于设计柔性微位移放大机构的选型设计具有很好的指导意义。
2 桥式微位移放大机构参数化设计
2.1 铰链选型设计
目前,常用的柔性微位移放大机构包括杠杆式放大机构和桥式放大机构两种,考虑到放大机构的精度、误差累积及结构紧凑性等问题,桥式放大机构比较适宜应用于精密定位平台,因此这里重点研究桥式放大机构的设计与性能。一种桥式柔性微位移放大机构如图4(a)所示。
图4中的相关字母符号释义如下:F为输入作用力;Din为输入位移;Dout为输出位移;S为输入位移作用点;P为输出位移作用点;a为椭圆型柔性铰链切口的长轴;b为椭圆型柔性铰链切口的段轴;t为直梁型柔性铰链与椭圆型柔性铰链的最小切割厚度;2L为直梁型柔性铰链的切口长度;l1为输出位移作用杠杆的力臂;l2为桥式杠杆的力臂;l3为输入位移作用杠杆的力臂。

图4 桥式微位移放大机构Fig.4 Bridge-type micro-displacement amplifier
图4(a)所示的桥式柔性微位移放大机构主要由H1,H2两个柔性铰链构成,在S点由驱动力F产生输入位移Din,经过放大机构对柔性铰链H1,H2的微弹性变形的放大,最终在P点输出位移Dout。H1,H2两个柔性铰链的类型直接影响到整个放大机构的放大增益。为了在P点得到更大的位移行程,使整个位移放大机构具有较大的放大增益,柔性铰链H1应当主要产生轴向线位移,即柔性铰链H1的输出位移形式中,轴向线位移的灵敏度要尽量高;柔性铰链H2应当主要产生旋转角位移,即柔性铰链H2的输出位移形式中,旋转角位移的灵敏度要尽量高。结合图3所示的4种柔性铰链柔度比λ的曲线可知,铰链H1应当选用直圆型或椭圆型柔性铰链,铰链H2应当选用直梁型或倒圆角直梁型柔性铰链。铰链H1和H2具体选用哪一种类型的柔性铰链,还应当结合具体的设计要求及材料的许用应力等因素综合考虑。一种桥式柔性微位移放大机构如图4(b)所示,其中铰链H1选用椭圆型柔性铰链,铰链H2选用直梁型柔性铰链。
2.2 参数化设计
桥式柔性微位移放大机构采用如图4(b)所示的结构。其中,铰链H1选用椭圆型柔性铰链(elliptical flexure hinge,简称EF),铰链H2选用直梁型柔性铰链(leaf type flexure hinge,简称LF)。从图4桥式放大机构的结构不难发现,桥式放大机构的输出位移主要取决于铰链H2的尺寸参数,因此,首先进行铰链H2的相关参数设计,其次再对铰链H1进行参数设计。
桥式放大机构选用合金钢加工,其弹性模量E=2.1×1011N/m2,泊松比为0.32。假设压电致动器的驱动力F=10 N;桥式放大机构杆长l1=l2=80 mm,两个柔性铰链H1,H2的间距l3=30 mm。需要说明的是,由于柔性铰链的厚度w对于柔性铰链的运动精度几乎没有影响[25],因此这里的参数化设计并不包含柔性铰链的厚度参数w。
参数化设计过程如下:首先给定基本参数,桥式微位移放大机构的材料性能参数、驱动力参数,以及其他基本几何尺寸同上。其次,给定柔度比λ=1,改变ε的大小,计算出桥式微位移放大机构的输出位移及最大应力。相关计算结果如表1所示。最后,根据柔性放大机构的放大性能及许用安全应力约束等条件合理选取两个柔性铰链的几何尺寸。
如表1所示,第1~第5组数据的变化规律表明,随着铰链H2最小切割厚度t逐渐变小,桥式微位移放大机构的输出位移Dout逐渐增大,这与上文对结构参数ε的分析结论一致;由于采用第5组数据时,机构内部最大应力σmax已经接近材料的许用应力,因此选用第4组数据,由此确定了铰链H2的最小切割厚度t。第6~第13组数据选用第12组数据,由此确定了铰链H2的切口长度参数L;同样,采用相同的参数设计方法分别依次确定铰链H1的相关尺寸参数t,a及b。但是从表1的数据可以发现,柔性铰链H1的结构几何参数,对于输出位移的影响并不如铰链H2的参数明显,这与上文的分析也是一致的。铰链H1的结构参数确定过程具体为:第14~第19组数据选用第16组数据确定铰链H1的最小切割厚度t;第20~第28组数据选用第22组数据确定铰链H1的切口参数a;第29~第35组数据选用第33组数据确定铰链H1的切口参数b;至此,全部参数确定,最终确定选用第33组数据。
表1 桥式放大机构尺寸参数化设计有限元计算结果
Tab.1 FEM calculation results of bridge-type amplifier mechanism′s geometry based on parametric design
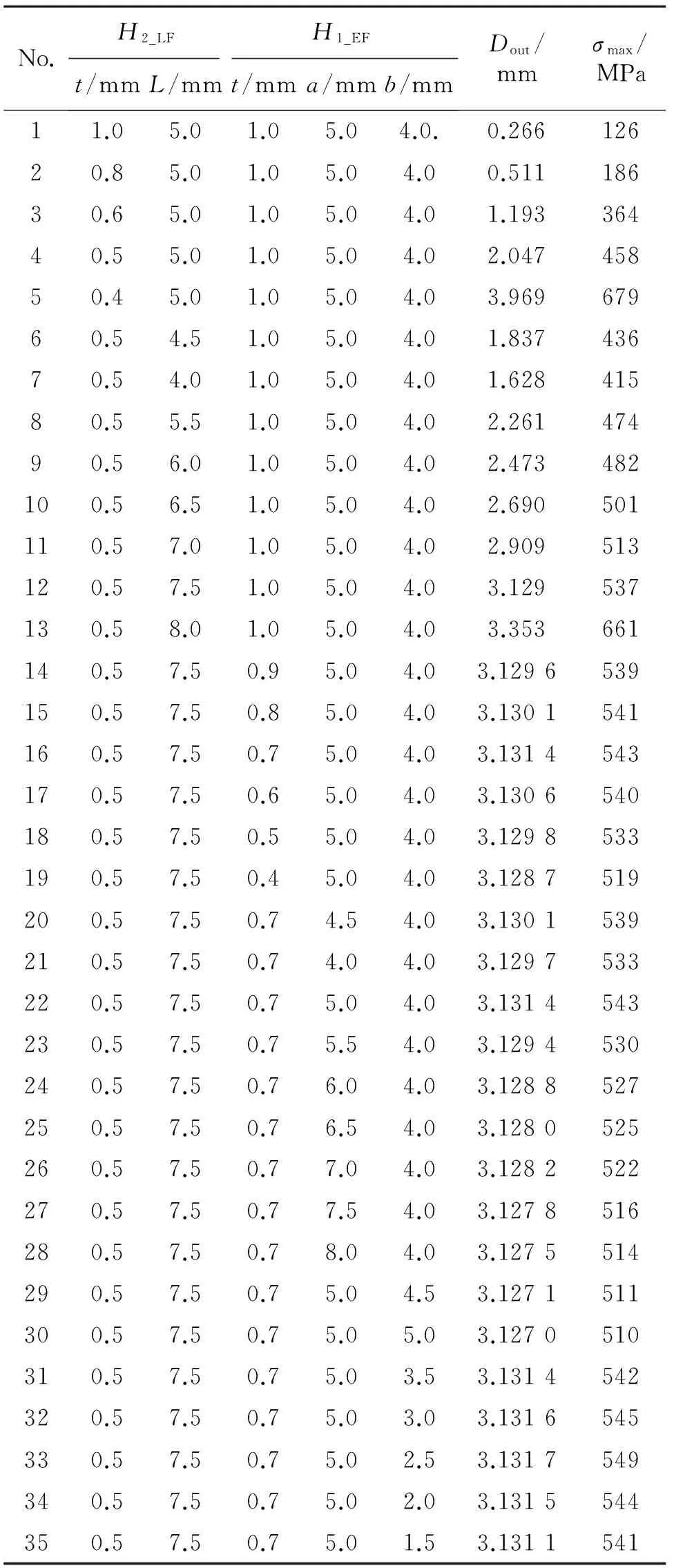
No.H2_LFH1_EFt/mmL/mmt/mma/mmb/mmDout/mmσmax/MPa11.05.01.05.04.0.0.26612620.85.01.05.04.00.51118630.65.01.05.04.01.19336440.55.01.05.04.02.04745850.45.01.05.04.03.96967960.54.51.05.04.01.83743670.54.01.05.04.01.62841580.55.51.05.04.02.26147490.56.01.05.04.02.473482100.56.51.05.04.02.690501110.57.01.05.04.02.909513120.57.51.05.04.03.129537130.58.01.05.04.03.353661140.57.50.95.04.03.1296539150.57.50.85.04.03.1301541160.57.50.75.04.03.1314543170.57.50.65.04.03.1306540180.57.50.55.04.03.1298533190.57.50.45.04.03.1287519200.57.50.74.54.03.1301539210.57.50.74.04.03.1297533220.57.50.75.04.03.1314543230.57.50.75.54.03.1294530240.57.50.76.04.03.1288527250.57.50.76.54.03.1280525260.57.50.77.04.03.1282522270.57.50.77.54.03.1278516280.57.50.78.04.03.1275514290.57.50.75.04.53.1271511300.57.50.75.05.03.1270510310.57.50.75.03.53.1314542320.57.50.75.03.03.1316545330.57.50.75.02.53.1317549340.57.50.75.02.03.1315544350.57.50.75.01.53.1311541
3 实 验
从参数化设计结果可知,柔性铰链H2相较于H1的结构参数,更能够影响整个桥式柔性微位移放大机构的输出位移行程。为此,将表2中所示的所有不同结构参数的放大机构全部加工出来进行实验对比的意义并不大,只需要验证参数化设计下的桥式柔性放大机构的输出位移与采用有限元设计方法得到的仿真值保持一致即可。为此选取表1中第33组数据,即选取柔性铰链H1和H2的各尺寸参数的最佳值进行验证。选用合金钢,经南京航空航天大学加工中心加工制造,采用线切割工艺加工而成的桥式柔性微位移放大机构,如图5所示。

图5 桥式柔性微位移放大机构实验研究Fig.5 Experiment study of bridge-type flexible micro-displacement amplification mechanism
对所选取的柔性铰链尺寸参数进行实验研究,所获得的输出位移数据如表2所示。仿真结果与实验结果的误差率为3.80%,产生误差的主要原因包括柔性放大机构在线切割加工中产生的精度误差,以及材料加工过程中内部产生的变形及预应力等。结果表明,本研究课题所提出的依据参数ε和λ,对桥式柔性微位移放大机构进行柔性铰链选型和参数化设计是可行且正确的,参数ε和λ对柔性铰链及柔性微位移放大机构的设计具有很好的指导作用。
表2 桥式柔性放大机构实验与仿真结果对比
Tab.2 Comparison of simulation and experiment results of bridge-type flexible amplification mechanism

No.H2_LFH1_EFDout/mmt/mmL/mmt/mma/mmb/mm仿真值实验值相对误差/%330.57.50.75.02.53.13173.01263.80
4 结 论
1) 面向常用的柔性铰链提出了新的结构参数ε。分析表明:减小最小切割厚度t,能够有效地增加柔性铰链的工作行程,包括旋转位移和拉伸线位移。
2) 提出了新的参数——柔度比λ,该参数反映了柔性铰链的主要输出位移形式的灵敏度。在相同的尺寸规格和外力作用下,直梁型柔性铰链和倒圆角型柔性铰链更倾向于输出旋转角位移αz,而直圆型柔性铰链和椭圆形柔性铰链则更倾向于输出轴向线位移Δx作为主要位移输出形式。
3) 结合具体的桥式柔性微位移放大机构,对放大机构中的柔性铰链作参数ε和λ的选型设计及参数化设计,并采用有限元仿真和实验的方法进行了验证。有限元仿真与实验结果均表明,根据参数ε和λ对柔性微位移放大机构中的柔性铰链进行选型设计,能够有效地提高桥式柔性微位移放大机构的输出位移与工作行程。基于柔性铰链的结构参数ε和柔度比λ对柔性放大机构进行参数化分析与设计,是可行且正确的,有利于这一类微位移柔性放大机构的设计与应用。
[1] Xu Qingsong. Design, testing and precision control of a novel long-stroke flexure micro-positioning system[J]. Mechanism and Machine Theory, 2013,70(6):209-224.
[2] 李庆祥,王东升,李玉和.现代精密仪器设计[M].2版.北京:清华大学出版社,2004:98-107.
[3] Zhang D, Gao Z, Malosio M, et al. A novel flexure parallel micromanipulator based on multi-level displacement amplifier with/without symmetrical design[J]. International Journal of Mechanics and Materials in Design, 2012,8(4):311-325.
[4] Bhagat U, Shirinzadeh B, Clark L, et al. Design and analysis of a novel flexure-based 3-DOF mechanism[J]. Mechanism and Machine Theory, 2014,74(4):173-187.
[5] Choi S B, Han S S, Han Y M, et al. A magnification device for precision mechanisms featuring piezoactuators and flexure hinges: design and experimental validation[J]. Mechanism and Machine Theory, 2007,42(9):1184-1198.
[6] Do T N, Tjahjowidodo T, Lau M W S, et al. Hysteresis modeling and position control of tendon-sheath mechanism in flexible endoscopic systems[J]. Mechatronics, 2014,24(1):12-22.
[7] Meng Qiaoling, Li Yangmin, Xu Jia. A novel analytical model for flexure-based proportion compliant mechanisms[J]. Precision Engineering, 2014,38(3):449-457.
[8] Kim J J, Choi Y M, Ahn D, et al. A millimeter-range flexure-based nano-positioning stage using a self-guided displacement amplification mechanism[J]. Mechanism and Machine Theory, 2012,50(2):109-120.
[9] 叶果,李威,王禹桥,等.柔性桥式微位移机构位移放大比特性研究[J].机器人,2011,33(2):251-256.
Ye Guo, Li Wei, Wang Yuqiao, et al. Analysis on displacement amplification ratio of a flexible bridge-type micro-displacement mechanism[J]. Robot, 2011,33(2):251-256. (in Chinese)
[10]宫金良,张彦斐,胡光学.考虑全柔性单元复杂变形的微位移放大机构刚度分析[J].北京工业大学学报,2013,39(12):1791-1797.
Gong Jingliang, Zhang Yanpei, Hu Guangxue. Stiffness analysis of micro-driving displacement amplifier module considering complex deformation of all flexible structure units[J]. Journal of Beijing University of Technology, 2013,39(12):1791-1797. (in Chinese)
[11]刘庆玲.柔性对称微位移放大机构性能分析方法的研究[J].工程设计学报,2013,20(4):344-347.
Liu Qingling. Study on the performance analysis methods of the compliant symmetric micro-displacement magnifying mechanism[J]. Chinese Journal of Engineering Design, 2013,20(4):344-347. (in Chinese)
[12]Bi Shusheng, Zhao Shanshan, Zhu Xiaofeng. Dimensionless design graphs for three types of annulus-shaped flexure hinges[J]. Precision Engineering, 2010,34(3):659-666.
[13]Lobontiu N. Compliance-based matrix method for modeling the quasi-static response of planar serial flexure-hinge mechanisms[J]. Precision Engineering, 2014,38(3):639-650.
[14]Lobontiu N, Cullin M. In-plane elastic response of two-segment circular-axis symmetric notch flexure hinges: the right circular design[J]. Precision Engineering, 2013,37(3):542-555.
[15]宫金良,胡光学,张彦斐.以刚度为目标的微位移放大模块闭环设计方法[J].机械工程学报,2012,48(15):58-64.
Gong Jingliang, Hu Guangxue, Zhang Yanpei. Closed loop design method of micro-driving displacement amplifier module targeting for stiffness[J]. Journal of Mechanical Engineering, 2012,48(15):58-64. (in Chinese)
[16]沈剑英,张海军,赵云.压电陶瓷驱动器杠杆式柔性铰链机构放大率计算方法[J].农业机械学报,2013,44(9):267-271.
Shen Jianying, Zhang Haijun, Zhao Yun. Calculation method of magnification ratio for lever-type flexure hinge mechanism driven by piezoactuator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(9):267-271. (in Chinese)
[17]李威,叶果,王禹桥,等.一种桥式微位移放大机构的性能研究[J].中国矿业大学学报,2011,40(2):310-314.
Li Wei, Ye Guo, Wang Yuqiao, et al. Study of properties of a kind of bridge-type micro-displacement mechanism[J]. Journal of China University of Mining & Technology, 2011,40(2):310-314. (in Chinese)
[18]Bolzmacher C, Bauer C, Schmid U, et al. Displacement amplification of piezoelectric microactuators with a micromachined leverage unit[J]. Sensors and Actuators A: Physical, 2010,157(1):61-67.
[19]Ma Hongwen, Yao Shaoming, Wang Liquan, et al. Analysis of the displacement amplification ratio of bridge-type flexure hinge[J]. Sensors and Actuators A: Physical, 2006,132(6):730-736.
[20]Xu Qingsong, Li Yangmin. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier[J]. Mechanism and Machine Theory, 2011,46(2):183-200.
[21]Choi K B, Lee J J, Hata S. A piezo-driven compliant stage with double mechanical amplification mechanisms arranged in parallel[J]. Sensors and Actuators A: Physical, 2010,161(1-2):173-181.
[22]Yu Yueqing, Feng Zhonglei, Xu Qiping. A pseudo-rigid-body 2R model of flexural beam in compliant mechanisms[J]. Mechanism and Machine Theory, 2012,55(9):18-33.
[23]于志远,姚晓先,宋晓东.基于柔性铰链的微位移放大机构设计[J].仪器仪表学报,2009,30(9):1818-1822.
Yu Zhiyuan, Yao Xiaoxian, Song Xiaodong. Design of micro-displacement amplifier based on flexure hinges[J]. Chinese Journal of Scientific Instrument, 2009,30(9):1818-1822. (in Chinese)
[24]赵磊,巩岩,华洋洋.直梁圆角形柔性铰链的柔度矩阵分析[J].中国机械工程,2013,24(18):2462-2468.
Zhao Lei, Gong Yan, Hua Yangyang. Compliance matrix analysis of corner-filleted flexure Hinge[J]. China Mechanical Engineering, 2013,24(18):2462-2468. (in Chinese)
[25]Tian Y, Shirinzadeh B, Zhang D, et al. Three flexure hinges for compliant mechanism designs based on dimensionless graph analysis[J]. Precision Engineering, 2010,34(1):92-100.

10.16450/j.cnki.issn.1004-6801.2016.05.018
国家自然科学基金资助项目(51375224);江苏高校优势学科建设工程基金资助项目
2015-01-08;
2015-04-13
TH122
卢倩,男,1983年7月生,博士生、讲师。主要研究方向为压电驱动技术及压电致动测试计量技术。曾发表《深切口椭圆柔性铰链优化设计》(《光学 精密工程》 2015年第23卷第1期)等论文。
E-mail:jackeylunuaa@126.com
简介:黄卫清,男,1965年4月生,博士、教授、博士生导师。主要研究方向为超声电机技术。
E-mail:mehwq@nuaa.edu.cn

