基于混沌理论的局域网流量预测

王石， 杨怀江， 董琰

(1.中国科学院长春光学精密机械与物理研究所，吉林，长春 130033；2.中国科学院大学，北京 100039；3.东北师范大学 信息化管理与规划办公室，吉林，长春 130024)



基于混沌理论的局域网流量预测

王石1，2，3， 杨怀江1， 董琰3

(1.中国科学院长春光学精密机械与物理研究所，吉林，长春 130033；2.中国科学院大学，北京 100039；3.东北师范大学 信息化管理与规划办公室，吉林，长春 130024)

局域网业务流中广泛存在自相似为特征的现象，并且自相似现象与混沌现象间存在紧密联系. 通过采用局域网流量对应的时间序列分析的方法进行研究，基于相空间重构思想，通过C-C算法计算嵌入维和延迟时间；利用小数据量法计算局域网流量时间序列的最大Lyapunov指数来判断其混沌特性；针对基于最大Lyapunov指数的预测方法中只考虑中心点的最邻近点对预测的决定性作用，而忽略了其邻近点邻域内其他各点对预测结果的影响的特点，提出了基于最大Lyapunov指数的加权邻域预测法；最后通过实测局域网流量预测验证方法的有效性.

混沌时间序列；小数据量法；局域网流量预测

互联网诞生以来，网络的设计者和研究者一直对网络流量的建模和预测进行不断的探索. 从早期的传统模型，如泊松模型、马尔可夫模型、回归模型到后来的自相似模型，如on/off模型、排队模型、FBM模型、FARIMA模型[1-7]. 传统模型的不足是当业务源数目增加时，突发性会被吸收，聚合业务会变得越来越平滑，而现代网络流量特性为高速、突发、自相似. 因此传统模型已不适合对现代网络流量进行准确描述. 自相似模型虽可以较好地描述网络流量的自相似性，但是存在假设条件严格、模型功能单一、计算量大等缺点. 已有学者发现局域网业务流中广泛存在着以自相似为特征的现象，并且与混沌现象间存在紧密联系，因此从混沌时间序列的角度来研究具有自相似特征的局域网流量是可行的. 本文通过采用局域网流量对应的时间序列分析的方法进行研究，基于相空间重构思想[8]，通过C-C算法[9]计算嵌入维和延迟时间，利用小数据量法[10]计算最大Lyapunov指数，判断时间序列的混沌特性并进行预测；针对基于最大Lyapunov指数的预测方法中只考虑到预测中心点的最邻近点对预测的决定性作用，而忽略了其邻近点邻域内其他各点对预测结果的影响的特点，提出了基于最大Lyapunov指数的加权邻域预测法；最后，通过对某高校出口流量数据的实验和分析来验证方法的有效性.

1 相空间重构

根据Takens理论，对于时间序列{xi}，i=1，2，…，N，如果能选定合适嵌入维数m，以时间延迟t重构相空间如下

(1)

相点总数M=N-(m-1)t. 如此得到的相空间在拓扑等价意义下与原混沌序列是微分同胚的，可以把有规律的轨迹(吸引子)恢复出来. 有多种方法可以计算m和t，H.S.Kim等提出C-C算法，该算法应用关联积分能同时估计出延迟时间t和嵌入时间窗tw；同时根据D.Kugiumtzis提出的延迟时间和嵌入维不应该是独立的量而是存在紧密的内在联系，并且满足关系式tw=(m-1)t的理论，进而计算出嵌入维m.

算法步骤：

① 嵌入时间序列的关联积分为

(2)

② 定义统计量

(3)

③ 为研究时间序列{xi}，i=1，2，…，N的非线性独立性并且消除虚假的时间相关性，式(3)的计算过程为将时间序列分成t个互不相交的子序列，然后采用分块平均的策略，即

(4)

④ 选择最大和最小的两个半径r，定义差量

(5)

ΔS(m，t)～t反映了时间序列的自相关特性，仿照求时延的自相关法原理，最优时延t可取ΔS(m，t)～t的第一个局部极小点. 此时表示重构吸引子轨道在相空间完全展开.

⑤基于BDS统计结果可以得到m，N，r的合理估计，这里取N=1 760；m=2，3，4，5；ri=ix0.5σ，i=1，2，3，4(σ表示时间序列标准差). 计算平均量

(6)

(7)

定义指标

(8)

Scor(t)极小点对应的时间即为嵌入时间窗tw.

⑥ 利用公式tw=(m-1)t及步骤④求出的时间延迟t可以计算出嵌入维m.

2 小数据量法

小数据量法是一种计算混沌时间序列的最大Lyapunov指数的方法. 最大Lyapunov指数可以定量描述初始状态靠得很近的相空间轨迹随时间变化按指数分离的程度；并且可以依据其估计系统的混沌水平和复杂度. 算法中用关联维数确定嵌入维数的方法计算量较大；结果易受参数选择的影响. 因此采用C-C算法来同时确定嵌入维数与时间延迟.

算法步骤：

① 对时间序列{xi}，i=1，2，…，N进行FFT变换，以能量光谱的平均频率的倒数估计平均周期P. 平均周期作为限制性条件可以保证估计最大Lyapunov指数的邻近点具有相近的初始条件并且按平均速率分离；

② 根据C-C算法确定的时间延迟t和嵌入维数m重构相空间Yi∈Rm；

③ 寻找相空间中每个点Yi的最邻近点Yj，并限制短暂分离，即

(9)

④ 对相空间中每个点Yi，计算出该邻点对的k个离散时间步后的距离di(k)，

(10)

⑤ 对每个k，求出所有i的lndi(k)平均值为

(11)

式中：q为非零di(k)的数目；h为采样周期.

用最小二乘法作出回归直线，该直线的斜率即最大Lyapunov指数λ1.

3 基于最大Lyapunov指数的预测法

最大Lyapunov指数可定量描述两个很靠近的初值所产生的轨道随时间推移按指数方式分离的现象[7-8]. 因此可以按照如下步骤预测：

① 根据由C-C算法确定的时间延迟t和嵌入维数m，重构相空间Yi∈Rm，相点总数M=N-(m-1)t；

② 选取预报中心点YM，找到YM最邻近点Yj，两相点各自随时间推移一步，其轨道距离将按指数分离，可表示为

(12)

式(12)中只有YM+1的最后一个分量xn+1是未知的，从而可以计算出原时间序列的一步预测值xn+1；

③ 依次随时间推移选取预测中心点YM+1，YM+2，…，利用步骤②预测值并重复执行步骤②，可以计算有限步推测值xn+2，xn+3，…；

④ 最大可预报时间依然可以依据此理论推测. 两最邻近相点Yi与Yj，各自随时间推移k步，其轨道距离按指数分离，可表示为

(13)

式中d(0)为两相点的初始距离.

可以认为上式超过临界C时，轨道发散到不可预言，这时所经历的时间就是临界时间，即最大可预报时间t0，并且有t0=lnC/λ1. 通常取C=e或更小，可得到最大可预报时间：t0=1/λ1.

4 基于最大Lyapunov指数的加权邻域预测法

基于最大Lyapunov指数的预测法只考虑了预测中心点与其最邻近点的距离对预测结果的决定性作用. 深入分析发现，最大Lyapunov指数对两个很靠近的初值所产生的轨道随时间推移按指数分离的定量描述只是一个带有主观因素的大略估计. 实际上在进行局域网流量预测时，由于舍入关系，按距离计算个别点的最邻近点有时存在多个点距离相等或舍入以后相等的情况. 预测中心点的最邻近点的邻域内其他各点距预测中心点的空间距离是非常重要的参数，预测的准确性往往取决于距中心点空间距离最近的那几个点. 因此将其作为一个拟合参数引入预测过程，在一定程度上可以提高预测的精度，并有一定的消噪能力.

算法步骤为：

① 根据由C-C算法确定的时间延迟t和嵌入维数m，重构相空间Yi∈Rm，相点总数M=N-(m-1)t；

② 选取预报中心点YM，确定其最邻近点及邻域各点Yj，j=1，2，…，k，选取点数k>m+1，太多没有必要，甚至影响预测效果. 依据基于最大Lyapunov指数预测法分别计算出邻域内各点对应的下一步预测值xn+1(j)，j=1，2，…，k；

③ 设临近点距中心点距离为dj，j=1，2，…k，其中d0为dj中最小值，即中心点与其最邻近点间距离. 定义权值

(14)

式中：θ为收敛参数，取θ=k；

则预测值可以表示为

(15)

④ 依次随时间推移选取预测中心点M+1，YM+2，…，利用步骤③预测值并重复执行步骤③，可以计算有限步推测值xn+2，xn+3，…；

⑤ 最大可预报时间同基于最大Lyapunov指数的预测法.

5 局域网流量的预测

所分析局域网流量数据来自某高校核心交换机联通出口数据. 测试时间为2014年5月10日至3月15日. 采样周期30 s，采样点数1 800个.

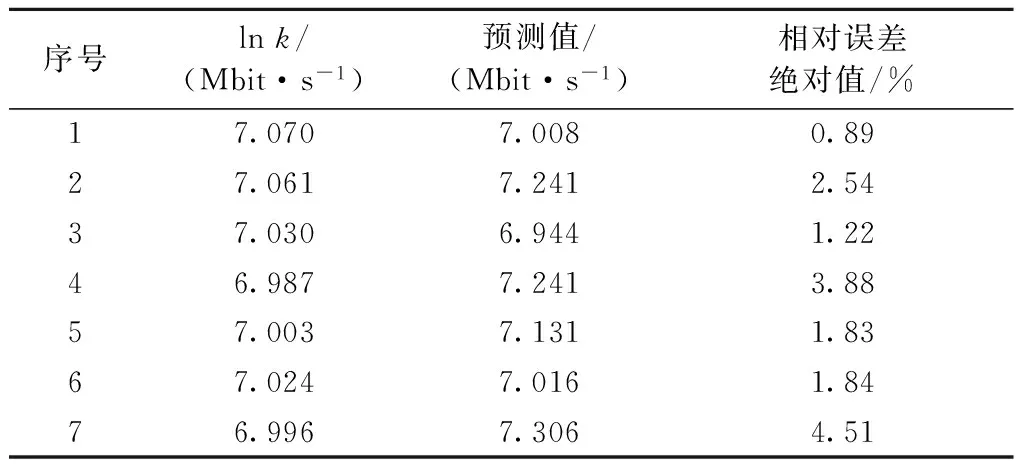
采用C-C算法计算出m=12，t=10. 利用以上参数基于改进的小数据量法计算最大Lyapunov指数λ1=0.148 9. 最大Lyapunov指数大于0，说明该时间序列具有混沌特征.t0=1/λ1=6.7，最大预测时间为7步. 根据基于最大Lyapunov指数的预测法及改进的加权邻域预测法分别做出了局域网流量时间序列后续7个点的预测值，见表1和表2.

表1 基于最大Lyapunov指数的预测法预测结果

Tab.1 Predicted results based on the largest Lyapunov prediction method

序号lnk/(Mbit·s-1)预测值/(Mbit·s-1)相对误差绝对值/%17.0707.0080.8927.0617.2412.5437.0306.9441.2246.9877.2413.8857.0037.1311.8367.0247.0161.8476.9967.3064.51

注：k为校园网联通出口实测流量数据

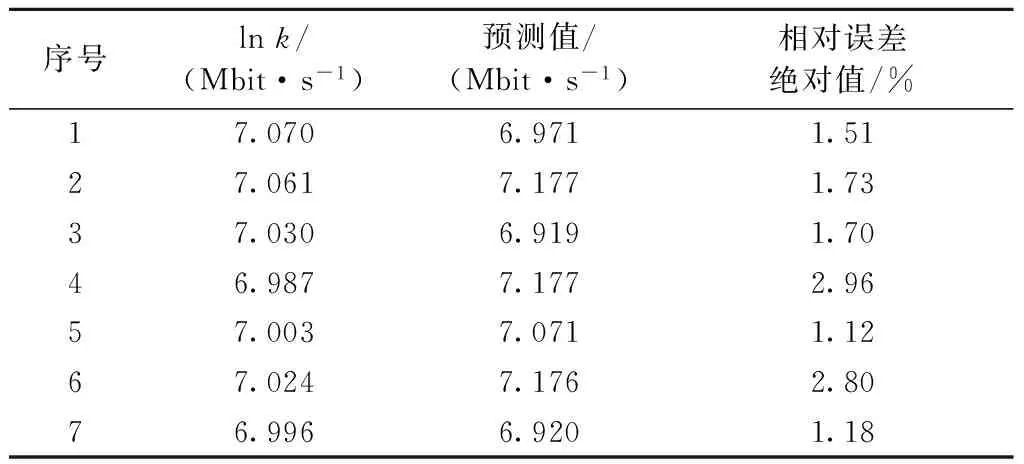
表2 基于加权邻域预测法预测结果

Tab.2 Predicted results based on the weighted neighborhood prediction method

序号lnk/(Mbit·s-1)预测值/(Mbit·s-1)相对误差绝对值/%17.0706.9711.5127.0617.1771.7337.0306.9191.7046.9877.1772.9657.0037.0711.1267.0247.1762.8076.9966.9201.18

注：k为校园网联通出口实测流量数据

由表1和表2的数据对比可知利用基于最大Lyapunov指数的预测法预测局域网流量数据相对误差绝对值在5%以内；利用基于最大Lyapunov指数的加权邻域法进行局域网流量预测相对误差绝对值在3%以内，预测精度有明显提高.

6 结 论

① 基于相空间重构理论，用C-C算法计算嵌入维和延迟时间，再利用小数据量法计算局域网时间序列的最大Lyapunov指数，可以通过最大Lyapunov指数是否大于0明确判断时间序列是否具有混沌性. 使基于混沌理论的局域网流量预测有了有力的理论依据. 需要注意的是，局域网流量在较长的时间范围内体现明显的周期性，周期为24 h，因此本方法在局域网流量时间序列的选取上有一定的限制条件，但是基于混沌理论的局域网流量短时预测比较可靠，是一种很有意义的尝试.

② 针对基于最大Lyapunov指数预测法没有利用到预报中心点的最邻近点邻域内其他各点的物理含义进行预测的情况，提出了基于最大Lyapunov指数的加权邻域预测法. 对实际局域网流量进行预测分析，结果表明改进的预测算法在不严重增加计算复杂度的前提下，有效提高了预测精度.

[1] Bonald T. The Erlang model with non-poisson call arrivals[J]. ACM Sigmetrics Performance Evaluation Review， 2006，34(1):276-286.

[2] Yang X S， Petropulu A P. The extended alternating fractal renewal process for modeling traffic in high-speed communication networks[J]. IEEE Trans On Signal Processing， 2001，49(7):1349-1363.

[3] Frost V， Melamed B. Traffic modeling for telecommunications networks[J]. IEEE Communications Magazine， 1994，32(3):70-81.

[4] Sarvotham S， Riedi R， Baraniuk R. Network and user driven alpha-beta on-off source model for network traffic[J]. Computer Networks， 2005，48(3):335-350.

[5] Krunz M， Makowski M. Modeling video traffic using M/G/∞ input processes[J]. IEEE Journal of Selected Areas in Communications， 1998，16(5):733-748.

[6] Norros I. A storage model with self-similar input[J]. Queueing System， 1994，16(3，4):387-396.

[7] Beran J， Sherman R， Taqqu M S， et al. Long-range dependence in variable-bit-rate video traffic[J]. IEEE Trans on Communications， 1995，43 (2-4):1566-1579.

[8] Takens F. Detecting strange attractors in turbulence[J]. Lecture Notes in Math，1981，898:361-381.

[9] Kim H S， Eykholt R， Salas J D. Nonlinear dynamics， delay times and embedding windows[J]. Physica D: Nonlinear Phenomena， 1999，127(1):48-60.

[10] Rosenstein M T， Collins J J， Deluca C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D: Nonlinear Phenomena， 1993，65(1):117-134.

(责任编辑：李兵)

Prediction in LAN Traffic Flow Based on Chaos Theory

WANG Shi1，2，3， YANG Huai-jiang1， DONG Yan3

(1.Changchun Institute of Optics， Fine Mechanics and Physics， Chinese Academy of Sciences， Changchun， Jilin 130033， China; 2.University of Chinese Academy of Sciences， Beijing 100039， China 3.Office of Information Management and Planning， Northeast Normal University， Changchun， Jilin 130024，China )

There exists widely the self-similarity in LAN traffic flow, and there is a close relationship between the self similarity characteristics and chaotic phenomena. The LAN time series of traffic flow were reconstructed in phase space theory. The embedding dimension and the delay time were computed by the C-C algorithm, and the largest Lyapunov exponent was then calculated via the small data method to determine its chaotic level. The weighted neighborhood prediction method was proposed and conducted considering the only decisive role of the nearest point on the center point based on the largest Lyapunov exponent while ignoring its neighborhood points on the predicting affection. The validation of the method was done by predicting the actual LAN traffic flow.

chaos time series; small data method; LAN traffic flow prediction

2015-03-11

吉林省教育厅“十二五” 科技与社科研究规划资助项目(2014B053)；吉林省科技厅吉林省自然科学基金资助项目(20140101189JC)

王石(1979—)，男，硕士，工程师，E-mail：wangs@nenu.edu.cn.

TP393

A

1001-0645(2016)06-0616-04

10.15918/j.tbit1001-0645.2016.06.012