基于关键零部件技术状态的机械产品定时维修间隔期优化方法
张耀辉,李林宏,徐玉国,郑 毅
(装甲兵工程学院 技术保障工程系,北京 100072)
基于关键零部件技术状态的机械产品定时维修间隔期优化方法
张耀辉,李林宏,徐玉国,郑 毅
(装甲兵工程学院 技术保障工程系,北京 100072)
针对描述产品故障规律的函数很难获得和基于产品故障规律进行定时维修间隔期优化的方法在实际应用中有一定困难的问题,研究了基于产品关键零部件技术状态的定时维修间隔期优化方法。分析了基于关键零部件技术状态信息优化定时维修间隔期的思路,介绍了基于关键零部件技术状态信息评估定时维修方案合理性的方法,分别建立了维修不足和维修过剩时定时维修间隔期的优化模型。
机械产品;定时维修;维修间隔期优化;技术状态
定时维修(time-based maintenance,TBM)是产品使用到预先规定的间隔期时,按事先安排的内容进行的维修[1]。目前,机械产品维修的主要维修方式是定时维修。定时维修的间隔期大小,对产品的可用度和维修费用具有重要的影响。如果产品故障具有安全性或任务性后果,定时维修间隔期过长则不足以保证产品所需的安全性或任务能力,过短则不经济;如果产品故障具有经济性后果,定时维修间隔期过长或过短都会影响经济性。
对于新产品,由于缺少产品故障规律的定量信息,其定时维修间隔期一般根据经验及相似产品的类比而确定,难以确定得十分合理,可能存在维修过剩或维修不足的问题,难以保证产品所需的安全性、任务性和经济性。因此,通过收集产品运行过程中的故障信息,分析产品的故障规律,据此优化产品的定时维修间隔期,一直是维修领域的研究热点问题。文献[2]给出了根据产品故障规律确定定时维修间隔期的一般模型。文献[3]通过机床故障维修记录数据的分析,经计算得到了机床的故障率函数,以单位时间内总的维修费用最小为优化目标,建立了基于故障率的机床定时维修间隔期优化模型。考虑定时维修后产品故障规律的变化,文献[4]和[5]引入等效役龄的概念,采用比例寿命回退模型对定时维修效果进行建模,建立了各次定时维修之间故障率函数的递推关系,以总维修费用最小为目标,建立了定时维修间隔期优化模型。文献[6]利用故障率衰减系数描述每次定时维修后故障率函数增长速度的递增,利用役龄减小系数反映每次定时性维修后设备年轻化导致的故障率函数时域延迟,以可靠度为约束条件,以单位时间平均维修费用最小为优化目标,建立了定时维修间隔期优化模型。针对多部件系统,文献[7]和[8]采用机会维修策略,根据系统的故障率特性,以最小化维修成本为目标,建立了机会维修控制限和定时维修间隔期优化模型。
目前关于定时维修间隔期优化的研究均以产品的故障率函数为依据。然而,定时维修的目的不仅仅是为了预防故障的发生,更重要的是为了保持产品的规定技术状态,以满足产品的性能指标要求。因此,产品可能在运行期间很少发生故障,甚至不发生故障,所以很难统计得出产品的故障率函数,因此基于产品故障规律的定时维修间隔期优化方法在实际应用中存在一定困难。为此,笔者研究基于产品关键零部件技术状态信息的定时维修间隔期优化方法。
1 定时维修间隔期优化思路
定时维修主要针对的是产品的渐进式时间相关故障或技术状态劣化。机械产品渐进式时间相关故障或技术状态劣化的主要原因是磨损。笔者主要研究以磨损为主要失效模式的机械产品定时维修间隔期的优化问题。
机械零件磨损的外在表现形态是表层材料的磨耗,一般情况下用磨损量来度量磨损程度。零件摩擦表面的磨损量随摩擦时间延续而逐渐增长。图1是正常工况下的磨损量实验曲线,它反映了磨损的一般规律,即磨损三阶段。
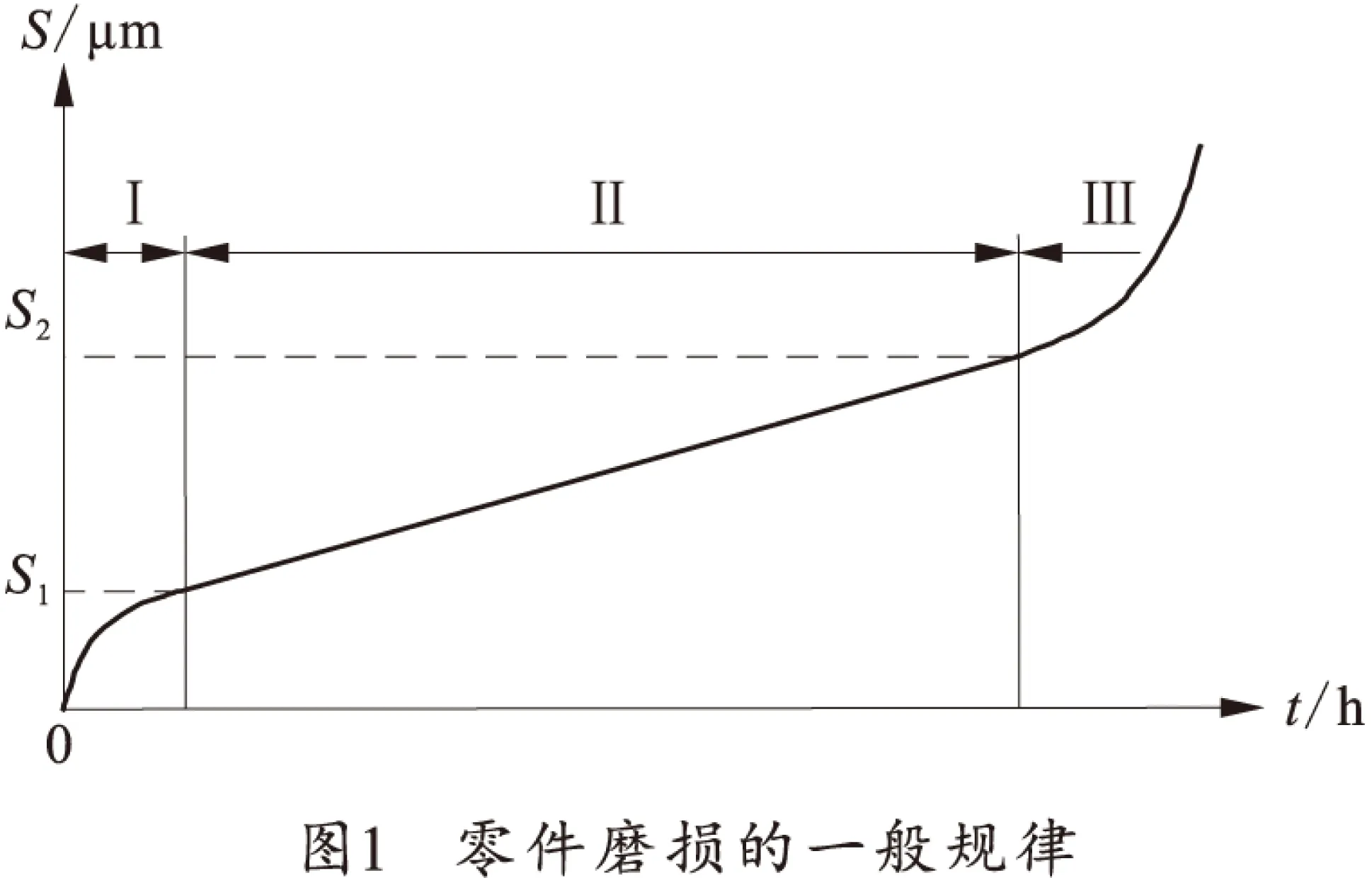
1)Ⅰ阶段为初期磨损阶段。对产品中的传动副而言是磨合过程。这一阶段的特点是在短时间内磨损量增长较快,磨损量很快达到S1。经过这一阶段以后,零件的磨损速度逐步过渡到稳定状态。磨合阶段结束后,应清除摩擦副中的磨屑,更换润滑油,才能进入满负荷正常使用阶段。
2)Ⅱ阶段为正常磨损阶段。摩擦表面的磨损量随着工作时间的延长而均匀、缓慢增长,属于自然磨损。在磨损量达到磨损极限值S2以前的这一段时间是零件的磨损寿命。
3)Ⅲ阶段为急剧磨损阶段。当零件表面磨损量超过磨损极限值S2以后如继续摩擦,其磨损量急剧增加,最终产品会出现故障或事故。其原因是:零件耐磨性较好的表层被破坏,次表层耐磨性显著降低;配合间隙增大,出现冲击载荷;摩擦力与摩擦功耗增大,使温度升高,润滑状态恶化、材料腐蚀与性能劣化等。
当零件磨损表面的磨损量达到磨损极限值S2时,就已经失效,不能继续使用。因此,应在这一阶段出现前进行预防性维修,降低故障率和减少维修工作量。这就是采用定时维修的理论依据。
对各类机械产品,主要摩擦副的磨损量的允许值或配合间隙的极限值都有具体的标准,由于精度、泄漏、能耗等方面的限制,允许磨损量一般小于磨损极限值S2。
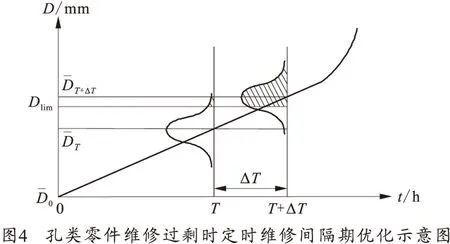
对于机械产品,一般根据其磨损极限和使用要求,规定了每一个零部件的免修极限Slim。在维修过程中,通过检测,如果反映零部件技术状态的尺寸、间隙等信息超出Slim,则零件应鉴定为报废件或待修件,进行报废或修理;如果没有达到Slim,则零件应鉴定为堪用件,可以继续使用。理论上堪用件的剩余寿命还应该够用1个定时维修间隔期,因此Slim一般远小于允许磨损量,更是远小于磨损极限值S2。
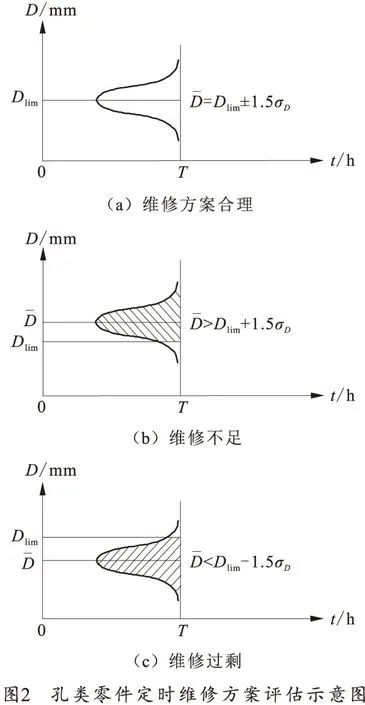
定时维修范围内的各个零部件,其最佳的维修间隔期各不相同,定时维修间隔期一般由其中的关键零部件决定。这里的关键零部件应该是对产品性能影响大、维修工作量大、维修费用高、磨损寿命较短的零部件。在定时维修过程中,可以通过对关键零部件磨损状态的检测,收集关键零部件的技术状态信息,评估维修方案是否合理,作为优化维修间隔期的依据。在维修过程中,如果反映零部件技术状态的尺寸、间隙等信息,基本在Slim附近,则表明其维修方案合理;如果大部分远远超出Slim,则表明维修不足,应该减小维修间隔期;如果大部分远远没有达到Slim,则表明维修过剩,应该加大维修间隔期。这就是优化定时维修间隔期的基本思路。
2 基于关键零部件技术状态的定时维修方案评估
根据公差与配合标准,可以将机械零部件分为孔和轴两大类。孔指由单一尺寸D确定的内表面,磨损会使该尺寸变大,D>Dlim为超出免修极限;轴指由单一尺寸d确定的外表面,磨损会使该尺寸变小,d 根据定时维修方案评估结果,对于维修不足和维修过剩2种情况,可以建立维修间隔期优化模型和优化维修间隔期。 3.1 维修不足时定时维修间隔期优化模型 (1) 即 (2) 给出直径D大于免修极限Dlim的允许概率PD>Dlim,根据正态分布的特性可以求得: 即 (3) 式中,系数z可根据(1-PD>Dlim)查正态分布数值表得出。 将式(3)带入式(2)可得: (4) 由式(4)即可求得维修不足时定时维修间隔期的减小量。 强调一点,当直径D大于免修极限Dlim的允许概率PD>Dlim=50%时,系数z=0,则有: (5) 3.2 维修过剩时定时维修间隔期优化模型 即 (6) 给出直径大于免修极限Dlim的允许概率PD>Dlim,根据正态分布的特性可以求得: 即 (7) 将式(7)带入式(6)可得: (8) 由式(8)可求得维修过剩时定时维修间隔期的增大量。 特别地,当直径大于免修极限Dlim的允许概率PD>Dlim=50%时,系数z=0,则有: (9) 定时维修间隔期的优化对于提高产品的可用度、降低维修费用具有重要意义。目前基于产品故障规律进行定时维修间隔期优化的方法,因故障率函数等描述产品故障规律的函数很难获得,在实际应用中有一定困难。在产品定时维修过程中,检测并统计关键零部件的技术状态信息,基于关键零部件技术状态信息进行定时维修间隔期优化,是一种简单实用的方法。 References) [1]中国人民解放军总装备部.GJB 451A—2005 可靠性维修性保障性术语[S].北京:总装备部军标出版发行部,2005. PLA General Armaments Department.GJB 451A—2005 Reliability, maintainability and supportability terms[S].Beijing:Military Standard Publication Distribution Department of PLA General Armaments Department.(in Chinese) [2]贾希胜. 以可靠性为中心的维修决策模型[M]. 北京:国防工业出版社,2007: 71-99. JIA Xisheng. The decision models for reliability centered maintenance[M]. Beijing: National Defense Industry Press, 2007: 71-79. (in Chinese) [3]王家海, 胡传胜, 张益飞. 基于故障率的机床预防性维修周期模型应用[J]. 组合机床与自动化加工技术, 2010(3): 43-46. WANG Jiahai, HU Chuansheng, ZHANG Yifei. Failure rate based preventive maintenance cycle model of machine tool[J]. Modular Machine Tool & Automatic Manufactu-ring Technique, 2010(3): 43-46. (in Chinese) [4]韩帮军, 范秀敏, 马登哲. 基于可靠度约束的预防性维修策略的优化研究[J]. 机械工程学报, 2003, 39(6): 102-105. HAN Bangjun, FAN Xiumin, MA Dengzhe. Research on the optimal preventive maintenance policy based on reliability constrains[J]. Chinese Journal of Mechanical Engineering, 2003, 39(6): 102-105. (in Chinese) [5]黄傲林, 李庆民, 黎铁冰,等. 劣化系统周期预防性维修策略的优化[J]. 系统工程与电子技术, 2014, 36(6): 1103-1107. HUANG Aolin, LI Qingmin, LI Tiebing,et al. Optimization of periodic preventive maintenance policy for deteriorating repairable system[J]. Systems Engineering and Electronics, 2014, 36(6): 1103-1107. (in Chinese) [6]杨春节, 童晟, 孙长生,等. 基于可靠度约束的混合预防性维修模型[J]. 浙江大学学报:工学版, 2008, 42(8): 1376-1379. YANG Chunjie, TONG Sheng, SUN Changsheng, et al. Hybrid preventive maintenance model based on reliability constraint[J]. Journal of Zhejiang University:Engineering Science, 2008, 42(8): 1376-1379. (in Chinese) [7]蔡景, 左洪福, 王华伟. 多部件系统的预防性维修优化模型研究[J]. 系统工程理论与实践, 2007, 27(2): 133-138. CAI Jing , ZUO Hongfu, WANG Huawei. A study on preventive maintenance optimization model for multi-unit system[J]. Systems Engineering-Theory & Practice, 2007, 27(2): 133-138. (in Chinese) [8]狄鹏, 黎放, 杨元. 基于机会维修策略的预防性维修优化模型研究[J]. 工程设计学报, 2012, 19(4):263- 267. DI Peng,LI Fang,YANG Yuan.Optimal preventive main-tenance model based on opportunistic maintenance policy[J]. Chinese Journal of Engineering Design, 2012, 19(4): 263-267. (in Chinese) Optimization Method of Time-based Maintenance Interval for Mechanical Equipment Based on the Key Part Technical Condition ZHANG Yaohui, LI Linhong, XU Yuguo, ZHENG Yi (Department of Technology Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China) A study was made of the optimization method of time-based maintenance interval based on the failure pattern in which failure rate function is difficult to acquire in that the reliability functions which characterize the failure pattern are generally unknown. Therefore, the optimization method of time-based maintenance interval based on the key part technical condition was researched in this paper. An analysis was made of the idea of optimizing the time-based maintenance interval based on the key part technical condition with the evaluation method of the rationale of the time-based maintenance concept based on the key part technical condition presented. The optimization models of time-based maintenance interval were constructed for inadequate maintenance and excessive maintenance respectively. mechanical equipment; time-based maintenance; maintenance interval optimization; technical condition 10.19323/j.issn.1673-6524.2016.03.020 2015-10-14 张耀辉(1960—),男,教授,博士,主要从事装备维修理论与技术研究。E-mail:zyh532@sohu.com TJ07 A 1673-6524(2016)03-0092-05
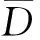
3 基于关键零部件技术状态的定时维修间隔期优化模型
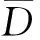
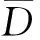
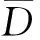
4 结束语

