基于蒙特卡洛模拟的身管疲劳寿命加速试验与分析

李家坤, 杨国来, 葛建立, 尹威华, 苏 艾

(南京理工大学 机械工程学院，江苏 南京 210094)



基于蒙特卡洛模拟的身管疲劳寿命加速试验与分析

李家坤, 杨国来, 葛建立, 尹威华, 苏 艾

(南京理工大学 机械工程学院，江苏 南京 210094)

为解决身管疲劳寿命试验时间长、费用高等问题，提出对身管进行加速寿命试验。基于蒙特卡洛方法对身管疲劳寿命的加速试验进行模拟，得到身管疲劳寿命的分布规律，同时对加速试验的基本假设进行验证，并估计出加速模型的参数。研究表明，身管的疲劳寿命在不同加速应力水平下均服从对数正态分布，加速因子与应力水平呈指数关系，通过加速模型估计的正常应力水平下身管疲劳寿命值与试验值之间的误差较小，验证了身管疲劳寿命加速试验的可行性。该研究为今后开展身管疲劳寿命的加速试验以估计身管疲劳寿命提供了一种理论方法。

疲劳寿命； 加速寿命试验；蒙特卡洛模拟；加速因子；加速模型

由于身管的寿命不可靠造成炸膛事故将直接危及战士的生命，因此必须对身管疲劳寿命的可靠性进行检验，目前被公认的身管疲劳寿命试验是实弹射击加液压循环试验，实弹射击目的是产生初始裂纹，火炮身管的疲劳寿命主要取决于裂纹的稳定扩展寿命，一般裂纹形成寿命可以忽略不计[1]。为解决火炮身管疲劳寿命试验时间长，费用高等问题，要对现行的试验方案加以改进。实践表明，加速寿命试验是一种大幅节省试验时间与成本的有效方法，是解决高可靠长寿命产品可靠性评估的一种重要技术途径。文献[2]采用蒙特卡洛仿真方法和MLE理论对步降加速寿命试验进行了理论分析。文献[3] 提出了依赖于加速模型的数据折算公式，对步加试验和步降试验进行仿真，证明了步降加速寿命试验有效提高分析精度和稳定性。文献[4]设计了一种改进遗传算法，采用Powell法对CQ2系列气缸进行了加速寿命试验，有效地降低了成本。文献[5]基于ADAMS建立了供弹机的虚拟样机模型,仿真得到了销轴与销孔在正常工况下和加速工况下配合的碰撞载荷谱与相对角速度谱，对供弹机加速寿命试验进行分析，证明了该加速寿命试验的可行性。

目前，对于身管的疲劳寿命的加速寿命试验研究较少，为此，笔者以某大口径火炮身管为研究对象，通过对身管疲劳寿命失效机理分析，采用ABAQUS对身管进行应力分析，并结合蒙特卡洛模拟方法模拟液压循环试验，得到不同加速应力水平下身管的疲劳寿命，并对结果进行评价分析，为确定身管疲劳寿命加速试验方法提供理论基础。

1 身管疲劳寿命的蒙特卡洛模拟

1.1 身管疲劳寿命的数学模型

身管的疲劳寿命主要取决于其裂纹扩展寿命，关于疲劳裂纹扩展速率模型类型有很多，著名的Paris-Erdogan裂纹扩展速率模型表达式为[1]

(1)

式中：C、m分别为材料常数；ΔK为应力强度因子，可表示为

(2)

式中：F为尺寸系数；a为裂纹深度；Δσθ为循环载荷中切向应力的幅值。

对式(1)进行积分，可得身管疲劳寿命的数学模型为

(3)

式中：a0为初始裂纹尺寸；ac为临界裂纹尺寸；NP为从初始裂纹扩展到临界裂纹尺寸的应力循环次数。

临界裂纹尺寸ac可以由材料的断裂韧性求出

(4)

式中：KIC为材料应变断裂韧性；σθmax为身管内壁切向应力最大值。

1.2 蒙特卡洛模拟

蒙特卡洛模拟法又称为统计模拟试验法或随机模拟法，以数理统计抽样为基础，以计算机计算为手段，通过有关随机变量的统计抽样试验，估计系统响应函数的统计量，求解工程技术近似解的一种数值计算方法。

利用蒙特卡洛模拟身管疲劳寿命的基本方法为：

1)确定身管疲劳寿命的数学模型NP=f(θi)= f(KIC,F,C,m,a0,ac) 中随机变量θ1，θ2，…，θn的参数分布。

2)定义模拟次数，产生在[0,1]区间服从均匀分布的随机数序列θj(j=1,2,…,n)，每模拟一次可以产生一组随机数列θ1，θ2，…，θn。

3)将每一次抽样的随机数列θ1，θ2，…，θn代入应力水平与疲劳寿命的数学模型。

4)估计系统响应f(θi)的分布特征，即疲劳寿命NP分布特征。

2 加速试验的基本假设检验与参数估计

2.1 加速试验基本假设

研究表明，身管疲劳寿命满足对数正态分布[1]。在满足对数正态分布LN(μ，σ2)的前提下，对身管疲劳寿命的加速试验有如下3条基本假设。

1)身管在正常膛压P0和加速应力水平P1，P2,…,Pk下身管的疲劳寿命都服从对数正态分布，采用自然对数进行分析，自然对数表达式为

(5)

式中，i=1，2，…，k。

2)身管在正常应力水平P0和加速应力水平P1，P2,…,Pk下寿命分布的对数标准差相同[6]，即

σ0=σ1=…=σk

(6)

上述两个假定表明，加速应力Pi不改变身管的寿命分布类型和对数标准差，只改变对数均值。

3)由于身管疲劳寿命满足对数正态分布，选择逆幂律模型作为加速模型，则身管寿命的对数均值μi与应力水平Pi之间有如下线性模型：

μi=a+bφ(Pi)

(7)

式中：a，b分别是待估参数；φ(Pi)是应力P的已知函数；μi是疲劳寿命的对数均值。

加速寿命试验必须满足以上3个基本假设，否则加速寿命试验不能成立。如果在上述3个假设成立的前提下，身管在正常应力水平P0和加速应力水平Pi(i=1,2，…，k)下对应的寿命分布函数之间关系为

F(t/Pi)=F(eμ(P0)-μ(Pi)t/P0)

(8)

由此可见，在身管疲劳寿命满足对数正态分布场合下，应力水平Pi对P0的加速因子表示为

β(P0,Pi)=e[μ(P0)-μ(Pi)]

(9)

式中,i=1,2，…，k。

2.2 加速试验的检验方法

根据前面假设，一个合理的加速寿命试验方案，其寿命分布形式不能改变，即在加速应力水平下身管的疲劳寿命也应满足对数正态分布，而且其对数标准差要相同，因此必须对加速应力水平下寿命分布规律和对数标准差σ进行检验。

假定在各加速应力水平Pi下，各对数标准差σi要相同，这意味着要检验假设H0：

σi=…=σk

对此假设可用巴特利特检验，为此用各应力水平Pi下的完全寿命数据计算对数方差的无偏估计

i=1,2，…,k

(10)

然后计算巴特利特检验统计量[7]B2和C的值，在假设H0成立的条件下，统计量B2/C近似服从自由度为k-1的χ2分布。在显著水平α下,当自由度为k-1的χ2分布上侧α分位数χα2(k-1)满足

χ2=B2/C≥χα2(k-1)

(11)

时，拒绝H0假设，否则接受H0假设。

2.3 加速模型的参数估计

(12)

(13)

再根据加速模型的一元线性回归模型

μi=a+bφ(Pi)，i=1，2,…，k

(14)

3 加速应力的选择原则

在对身管进行加速寿命试验时，不能改变身管的失效机理，否则可能使试验变得毫无意义。疲劳寿命的加速试验采用的是加大身管内壁的压力来进行加速试验，加速应力不超过身管弹性极限压力。自紧身管弹性极限压力可以用下式表示[1]:

(15)

式中：σs为屈服极限；R1、R2分别为身管内外半径；σθa为自紧身管内表面切向残余应力。

当加速应力水平P1，P2，…，Pk选定以后，可以根据有限元模型计算最大切向应力σθ1max，σθ2max，…，σθkmax。

4 数值仿真分析及其结果

以某大口径自紧身管[1]为例，自紧压力为886 MPa，身管材料牌号为PGrNi3MoV,通过ABAQUS有限元软件计算身管内壁切向残余应力σθα。取身管四分之一圆环截面，采用对称约束，如图1所示。

通过对内表面加载886 MPa的压力作为自紧压力，并考虑身管材料的鲍兴格效应，对身管的自紧过程进行模拟仿真，得到身管内表面切向残余应力为-824 MPa,由式(15)计算得到该身管的弹性极限压力为767.2 MPa。选择4组应力水平分别为P1=450 MPa、P2=550 MPa、P3=650 MPa、P4=750 MPa作为加速应力。

以自紧压力产生的自紧残余应力为初始条件，分别加载不同加速应力。通过有限元模型计算的最大切向应力结合身管疲劳寿命数学模型与蒙特卡洛模拟试验方法，通过1 000次模拟，身管的疲劳寿命分布及检验结果如表1所示。

表1 各加速应力水平下身管疲劳寿命分析

由表1可知，在显著水平α=0.05下，K-S检验值均大于0.05，则在显著水平α下接受原假设，即在各加速应力水平下，身管的疲劳寿命均服从对数正态分布，与正常压力下寿命分布类型相同，满足加速模型的第1条基本假设。

通过计算巴特利特统计量[9]得到B2=6.452，C=1.000 2，由此可得巴特利特检验统计量

χ2=B2/C=6.451

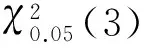
利用仿真得到的4组加速应力水平下身管的疲劳寿命数据，以加速应力为横轴，以身管疲劳寿命为纵轴，不同加速应力水平下身管疲劳寿命分布和不同分位寿命建立的加速模型如图2所示。

(16)

在可靠度为0.999时，应力水平与加速因子[9]关系如图3所示。

由此可以得出结论，在加速应力水平允许的范围内，加速因子随着加速应力水平的增大呈指数递增关系，其拟合优度较高。根据模拟值与试验值的比较分析，在加速应力水平下进行试验平均比正常应力水平下进行试验效率要提高2.99倍。因此，对身管疲劳寿命进行加速试验是一种可行的办法，这对加快试验进程、节省试验经费具有重要意义。

5 结论

1)在正常应力水平和加速应力水平下身管疲劳寿命均服从对数正态分布，而且其寿命分布的对数标准差相同。

2)身管疲劳寿命的对数均值随着身管内壁最大膛压的增大呈直线递减关系，加速因子与最大膛压值呈指数递增关系。

3)在可靠度为0.999时，通过加速模型估计的正常应力水平下身管疲劳寿命值与试验值之间的误差较小，建立的加速模型具有较好的预测效果。

4)在加速应力水平下试验比正常应力水平下试验效率提高了2.99倍。

5)该研究可有效缩短试验周期，验证了身管疲劳寿命加速试验的可行性，为身管疲劳寿命加速试验的开展提供了一定的理论依据。

)

[1]曾志银,张军岭,吴兴波.火炮身管强度设计理论[M].北京：国防工业出版社,2004.ZENG Zhiyin, ZHANG Junling, WU Xingbo. Strength design theory on gun tube[M]. Beijing: National Defense Industry Press, 2004.(in Chinese)

[2]潘刚，梁玉英，吕萌，等.步降加速寿命试验优化设计Monte-Carlo仿真[J].电光与控制，2013,20(4)：77- 80.

PAN Gang, LIANG Yuying, LYV Meng, et al. Optimal design of step-down-stress accelerated life test based on Monte-Carlo simulation[J]. Electronics Optics & Control,2013, 20(4):77-80. (in Chinese)

[3]谭伟，师义民，孙玉东. 步降应力加速寿命试验的可靠性仿真[J]. 计算机仿真,2011,28(12) ：80-83.

TAN Wei, SHI Yimin, SUN Yudong. Reliability simulation for step-down-stress accelerated life testing[J]. Computer Simulation,2011,28(12):80-83.(in Chinese)

[4]付永领,韩国惠,王占林,等. CQ2系列气缸加速寿命试验优化方法研究[J].兵工学报,2009,30(11)：1493- 1498.

FU Yongling, HAN Guohui, WANG Zhanlin, et al. Research on optimization method for accelerated life test of CQ2-series cylinder[J]. Acta Armamentarii, 2009,30 (11):1493-1498. (in Chinese)

[5]金朝,狄长春,秦俊奇，等. 某型供弹机关重件磨损加速寿命试验仿真[J].火力与指挥控制，2012,37(12)：167- 170.

JIN Zhao, DI Changchun, QIN Junqi, et al. Simulation and research of accelerated life testing about key components of feeder[J]. Fire Control & Command Control,2012, 37(12): 167-170. (in Chinese)

[6]ALJAZ P, JOZE T. An accelerated multilevel test and design procedure for polymer gears[J]. Materials and Design,2015,65(1): 961-973.

[7]XIAO L, LOON C T. Planning sequential constant-stress accelerated life tests with stepwise loaded auxiliary accele-ration factor[J]. Journal of Statistical Planning and Infe-rence,2010(140): 1968-1985.

[8]JINSUK L, RONG P. A GLM approach to step-stress accelerated life testing with interval censoring[J]. Journal of Statistical Planning and Inference,2012(142):810- 819.

[9]茆诗松,王玲玲.加速寿命试验[M]．北京：科学出版社，2000:138-191.

MAO Shisong， WANG Lingling．Accelerated life test[M]．Beijing：Science Press,2000: 138-191．(in Chinese)

Accelerated Test and Analysis of Gun Barrel Fatigue Life Based on Monte-Carlo Simulation

LI Jiakun, YANG Guolai, GE Jianli, YIN Weihua, SU Yi

(Mechanical Engineering College, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

For the purpose of solving the problem of too much time and the high cost of gun barrel fatigue life test, the suggestion of applying accelerated life test to the gun barrel fatigue life is made. Based on the simulation of Monte-Carlo method of gun barrel accelerated life testing, the distribution law of the barrel fatigue life was obtained. At the same time, the basic hypotheses are verified with the parameters of the accelerated model estimated. The study shows that the fatigue life of the barrel conforms to logarithm normal distribution under different acceleration stress levels, the relationship between the acceleration factor and the stress level is index correlation. The error of gun barrel fatigue life in estimated normal stress by using acceleration model is very small compared with that of the test results. These analyses and conclusions verified the feasibility of accelerated life tests, which provides a theoretical support for accelerated life test in the evaluation of gun barrel fatigue life.

fatigue life; accelerated life test; Monte-Carlo simulation; acceleration factor; acceleration model

10.19323/j.issn.1673-6524.2016.03.018

2015-08-20

国家重点基础研究发展计划项目(51319702)

李家坤(1988—)，男，硕士研究生，主要从事火炮寿命问题与可靠性分析技术研究。E-mail：jiakunzf20@163.com

TJ303+.1

A

1673-6524(2016)03-0084-04