基于代理模型的航空燃油泵空化性能分析

熊英华， 刘影, *， 赵兴安， 孙华伟， 王国玉， 高德明

1.北京理工大学 机械与车辆学院， 北京 100081 2.中航工业集团公司 南京机电液压工程研究中心， 南京 211106

基于代理模型的航空燃油泵空化性能分析

熊英华1， 刘影1, *， 赵兴安1， 孙华伟2， 王国玉1， 高德明1

1.北京理工大学 机械与车辆学院， 北京 100081 2.中航工业集团公司 南京机电液压工程研究中心， 南京 211106

基于代理模型的整体敏感度分析方法，对影响燃油泵空化性能的结构参数(即诱导轮出口安放角和叶轮进口安放角)进行了分析，得到影响泵空化性能的主要因素，并对燃油泵的结构参数进行了优化。研究中，采用基于旋转修正的k-ε湍流模型及Zwart空化模型对优化前后的燃油泵空化流场进行了计算。结果表明：在一定变化范围内，叶片安放角对燃油泵的外特性影响较小，对燃油泵空化特性影响较大；其中，叶轮进口安放角对燃油泵空化性能有较大影响，随叶轮进口安放角的增大，燃油泵空化性能呈先下降后上升的变化趋势；优化后诱导轮出口安放角和叶轮进口安放角分别增大了4.4° 和3.2°，满足Pareto最优解，燃油泵的空化性能较优化前提高了18%左右。

燃油泵； 代理模型； 湍流模型； 空化性能； 优化分析

燃油泵是航空发动机燃油系统中的重要组成部分，其性能对航空发动机的可靠、稳定运行具有重大影响[1]。相比于柱塞泵和齿轮泵，离心泵具有体积小、重量轻、抗燃油污染能力强和可靠性高等优点，因此通常用作主燃油泵。

航空燃油泵相比于普通离心泵，其流体介质为航空燃油，工作环境为高温低压，且具有流量大、转速高等特点，易发生空化现象。因此空化问题已成为影响燃油泵性能的主要问题之一，也是燃油泵性能优化中亟待解决的难点之一[1]。薛梅新等[2]针对某型航空发动机加力燃油泵隔舌空蚀破坏，采用滑移网格技术模拟泵内非定常流场，揭示了压出室在非设计工况下的内流特征，研究了隔舌处的空化机理；殷吉超等[3]对某型高速加力燃油离心泵内流场和空化过程进行了二维数值仿真，分析了空化易发生的位置以及排出管对空化发生的影响，对预测并克服空化发生有指导意义。针对燃油泵的空化问题主要通过结构优化设计进行解决，目前传统的离心泵结构优化方法[4]主要有：试验优化设计[5]、速度系数法优化设计[6]、损失极值法优化设计[7]、计算流体力学(CFD)优化设计[8]以及多工况优化设计[9]5种。传统离心泵优化方法虽然已广泛应用，但具有一定的局限性，需要大量准确的公式推导，且部分参数的确定有赖于设计者的经验和试验结果，增加了优化设计的难度和时间周期。近几年发展起来的代理模型(Surrogate Model)方法避免了传统优化方法的不足，可以有效地建立优化变量与目标变量之间的关系，并可得到多目标的优化结果，该方法适用范围非常广泛。Goel等[10]采用代理模型的方法对泵的叶片几何形状进行了优化，取得了理想的结果。杨卓懿等[11]利用响应面模型对潜器的艇型进行了优化，不但效率得到提高，优化的效果也得到了保证；吴钦和王国玉[12]利用代理模型分析方法对考虑了模型参数和物质属性的Merkle空化模型在低温介质空化流动计算中的应用进行评价和优化，提高了模型的预测能力。

为提高燃油泵的空化性能，本文采用代理模型优化方法对设计工况下燃油泵的结构参数进行优化分析；利用整体敏感度分析方法评价了诱导轮出口安放角和叶轮进口安放角对燃油泵空化性能和外特性的影响；采用数值计算方法，对获得的参数最优解进行验证，并对优化后燃油泵空化流场进行了分析。

1 数值计算方法

1.1 控制方程

采用均质平衡流模型，基于Favre平均的Navier-Stokes方程为

(1)

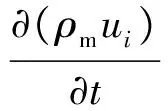
(2)

(3)

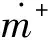
1.2 湍流模型

采用基于旋转修正的k-ε湍流模型[13]，标准k-ε湍流模型方程形式为

(4)

(5)

式中：ρ为燃油密度；ε为湍动能耗散；k为湍动能；Pt为湍动能生成项；σk与σε均为湍流模型常数，采用基于局部涡旋运动效应对标准k-ε湍流模型k方程中的Pt进行修正，修正系数fr为

Pt→Pt·fr

(6)

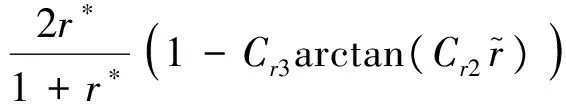
(7)

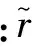
1.3 空化模型

计算采用Zwart空化模型[14]，即

(8)

(9)

式中：αnuc为空化核子体积分数，取5×10-4；RB为空泡直径，取1×10-6m；ρ和ρv分别为当地压力和饱和蒸汽压；凝结系数Ccond和蒸发系数Cvap分别为0.01和50。

1.4 几何及边界条件设置

对某型号航空燃油泵的空化流动进行计算，燃油泵结构如图1所示，其主要几何尺寸及设计工况参数如下：诱导轮轮缘直径D1=0.06 m，叶片数Z1=3，轮毂比R1=0.3；叶轮进口直径D2=0.06 m，叶片数Z2=4，进口轮毂比R2=0.3；泵入口直径D3=0.072 m，泵出口直径D4=0.07 m；设计转速n=10 000 r/min，设计流量Q=12.6 kg/s。

燃油泵模型采用混合网格划分，其中缩放管和蜗壳利用Ansys-ICEM 14.0划分非结构化网格，诱导轮、叶轮和导叶利用Ansys-TurboGrid 14.0划分结构化网格，近壁面进行网格加密，保证y+=ρlΔyuτ/u1≈1(其中Δy为距离壁面最近一层网格厚度；uτ为壁面摩擦速度；u1为主叶轮进口圆周速度)，网格质量良好。模型网格数经过检查，当计算外特性的变化小于2%时认为网格数影响可以忽略，生成的网格总数为134万。

图1 燃油泵三维模型图Fig.1 Three-dimensional model of fuel pump

计算采用总压入口、质量流量出口边界，叶片及轮缘轮毂均采用无滑移壁面边界，壁面函数为标准壁面函数，以单相计算结果为初值，进行迭代计算空化流动。计算采用的流动介质为20 ℃下RP-3航空燃油[15]，其密度、饱和蒸汽压和运动黏度分别为：ρ=780 kg/m3、pv=1 329 Pa、ν=1.48×10-6m2/s。

1.5 数值计算方法验证

为了对网格和数值计算方法进行验证，图2和图3分别给出了燃油泵在转速(7 800 r/min)下，试验和数值计算得到的外特性曲线和空化特性曲线。图中扬程系数ψ、流量系数φ分别为燃油泵扬程、流量的无量纲数，泵有效空化余量NPSHa表示泵进口处单位重量液体超过空化压力水头的能量，其定义分别为为体积流量，pin和pv分别为泵的入口压力和燃油饱和蒸汽压。

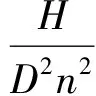
(10)

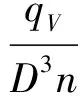
(11)

(12)

式中：H为总扬程；D为出口直径；n为转速；qV

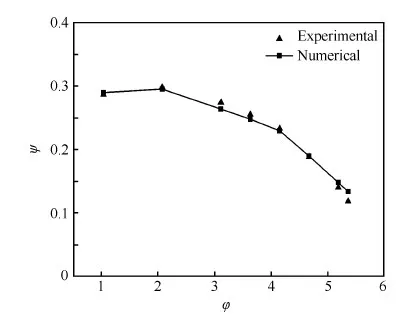
图2 燃油泵外特性曲线Fig.2 External performance of fuel pump

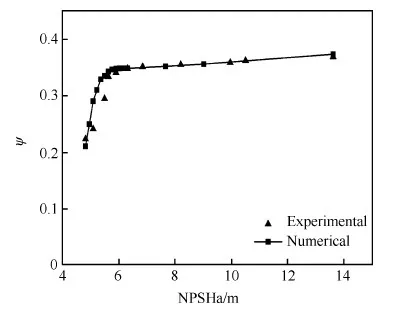
图3 燃油泵空化特性曲线Fig.3 Cavitation characteristics of fuel pump

对比试验与数值计算结果可以看出，计算得到的外特性曲线试验结果一致性较好，误差在3%左右；空化特性曲线数值与试验结果变化趋势一致且误差较小，计算得到的必须空化余量NPSHr为5.2 m，试验得到的NPSHr值为5.5 m，误差在5%左右。由此说明，本文所采用的数值计算方法可以较准确地预测燃油泵空化特性。

2 结果与分析

2.1 空化流动数值计算结果分析

燃油泵空化性能研究中，泵的必须空化余量NPSHr为衡量泵空化性能的一个重要参数，NPSHr值越小说明泵的空化性能越好。工程上规定，当泵的扬程下降3%时，认为泵进入空化状态，此时装置的有效空化余量NPSHa等于泵的必须空化余量NPSHr。燃油泵主叶轮NPSHr计算公式[16]为

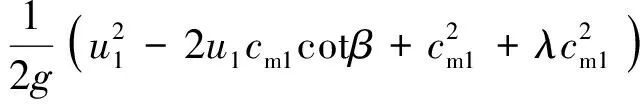
(13)

式中：c1、ω1和u1分别为主叶轮进口稍前的绝对速度、相对速度和圆周速度；cm1和β为轴面速度和主叶轮进口相对流动角；λ为主叶轮进口压降系数，通常取为0.2～0.3。从式中可以看出，在给定转速和流量工况下，NPSHr值与cm1和β大小相关，而cm1值受诱导轮出口安放角βb1和主叶轮进口直径D1影响，β值与主叶轮进口安放角βb2相关。受实际工程应用背景及燃油泵其他相关部件的影响，主叶轮进口直径无法改变，因此本文将主要研究诱导轮出口安放角βb1和主叶轮进口安放角βb2对燃油泵空化性能的影响。

图4给出了不同Δβb1和Δβb2、设计工况下燃油泵空化特性曲线。其中，Δβb1和Δβb2分别表示相对于原模型βb1和βb2的改变量，正值表示沿攻角增大的方向。从图中可以看出，燃油泵的有效空化余量NPSHa较大时，扬程基本不变，当NPSHa减小到泵的必须空化余量值时，燃油泵发生空化，扬程迅速下降。故设计参数Δβb1和Δβb2对燃油泵的最大扬程及必须空化余量均有显著影响。

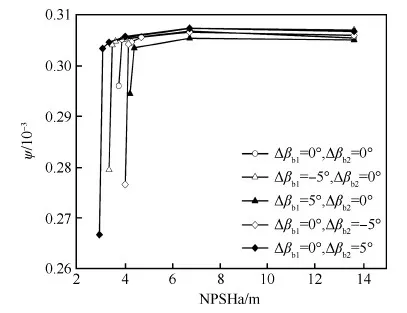
图4 不同Δβb1和Δβb2燃油泵空化特性曲线Fig.4 Cavitation characteristics of fuel pump with different Δβb1 and Δβb2

2.2 燃油泵空化性能及外特性优化

与普通离心泵相比，带诱导轮的燃油泵叶轮流动冲角同时受诱导轮出口安放角βb1和叶轮进口安放角βb2的影响，然而，通过数值计算的方法寻求最优结构参数，计算量大且计算周期较长，因此采用合理、高效的数值优化方法获取空化性能和外特性最优时燃油泵的结构参数至关重要。本节将利用基于方差的量纲归一化整体敏感度分析方法对影响燃油泵空化性能和外特性的结构参数βb1和βb2的变化量Δβb1和Δβb2进行评价，并采用代理模型优化分析方法获得空化性能和外特性最优时燃油泵的结构参数。

2.2.1 代理模型优化方法

代理模型优化方法的实质是通过离散的数据点(即设计点)，建立精度较高的数学模型，拟合出反映目标变量和自变量之间关系的函数，分析目标变量对自变量的敏感性以及对自变量取值进行寻优，代理模型优化方法的主要流程参见文献[14]。

本文选取Δβb1和Δβb2作为代理模型的自变量，选取燃油泵的必须空化余量NPSHr和无空化扬程系数ψ作为代理模型的目标变量。根据燃油泵叶片的结构参数，确定自变量Δβb1和Δβb2的取值范围为：-5°～5°。结合面心立方法(Face-centered Central Composite Designs，FCCD)和拉丁超立方法(Latin Hypercube Sampling，LHS)生成30个样本点，根据此30组数值计算的结果分别建立项式响应面近似模型(PRS)、Kriging模型(KRG)、辐射神经元网络近似模型(RBNN)[17]、Shepard 模型(SHEP)[18]、支持向量回归模型(SVR)[19]以及加权平均值近似相应模型(WAS)[20]。选取PRESS[21]作为各代理模型的准确度的评价指标，其表达式为

(14)

表1给出了各代理模型对目标变量的拟合误差，从中可以看出，不同代理模型对目标变量的拟合误差各不相同，其中WAS模型拟合误差最小，因此选择该模型的拟合结果对目标变量做进一步分析。该模型根据单个模型中误差最小的PRS、SHEP和SVR 3种模型各自的拟合精度，通过加权系数将模型进行整合，拟合得到的结果为

(15)

(16)

表1 不同代理模型拟合误差Table 1 Error estimates for different surrogate models

2.2.2 燃油泵空化性能与外特性敏感性分析

敏感度分析是指利用代理模型对燃油泵在设计工况下的数值计算结果进行拟合，比较自变量的偏方差和总方差以获得自变量Δβb1和Δβb2对目标变量NPSHr和ψ的重要程度分析，代理模型敏感度定义为

(17)

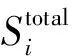
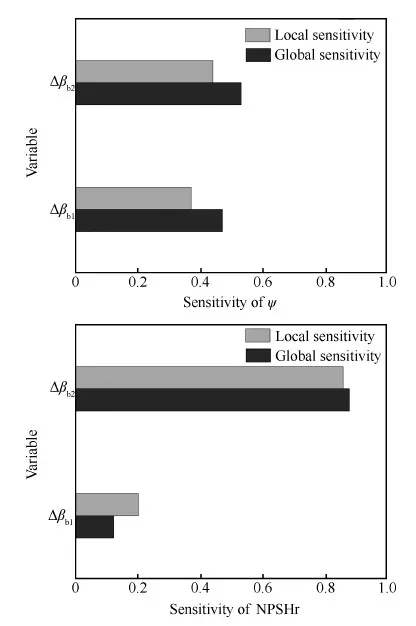
图5 WAS模型自变量对目标变量整体和局部敏感度分布Fig.5 Sensitivity indices of main and total effects of different variables using WAS

图6给出了自变量对目标变量整体敏感度具体分布情况，从中可以看出，Δβb2在目标变量ψ的敏感度分析中所占比重大(53%)，Δβb1的比重为47%，说明目标变量ψ受Δβb2影响稍大一些；而在对目标变量NPSHr的敏感度分析中，各自变量的敏感度差距较大，Δβb1所占比重为12%，而Δβb2的比重为88%，说明目标变量NPSHr主要受Δβb2的影响。

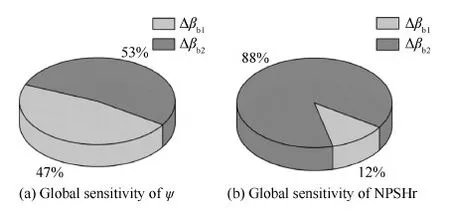
图6 WAS模型自变量对目标变量整体敏感度分布 Fig.6 Sensitivity indices of global effects of different variables using WAS

为了进一步分析自变量对目标变量的影响规律以及敏感度，根据WAS代理模型计算结果，图7 给出了目标变量ψ和NPSHr随自变量Δβb1和Δβb2的变化情况。从图7(a)可见，沿X轴方向随着Δβb1的减小，ψ呈现梯度式增大，但变化幅度较小；沿Y轴方向随着Δβb2的增大，ψ值整体呈现逐渐增大的趋势，且变化的幅度较大，说明ψ对Δβb2变化更敏感；从图7(b)可见，NPSHr的变化主要表现为沿Y轴方向随着Δβb2的增加而减小，且变化范围大，说明Δβb2对NPSHr影响显著，与上述敏感度分布情况一致。这是由于带诱导轮燃油泵主要做功的部分为主叶轮，且空化主要发生在主叶轮的进口前沿并向叶轮流道内发展，因此主叶轮的几何结构参数对燃油泵的性能影响更大。

2.2.3 燃油泵结构参数优化

在自变量空间中随机生成104个均匀分布的点，WAS模型拟合得到的结果在目标变量空间中的分布情况如图8所示(蓝色点集)。由图可知，通过燃油泵结构参数优化来提高空化性能是一个多目标优化问题，不存在最优解，所有可能的解构成Pareto最优解集(红色点集)，它是由只满足一个目标变量取最佳值条件的点组成[14]。

图7 目标变量随自变量变化趋势Fig.7 Variation of objectives with variables

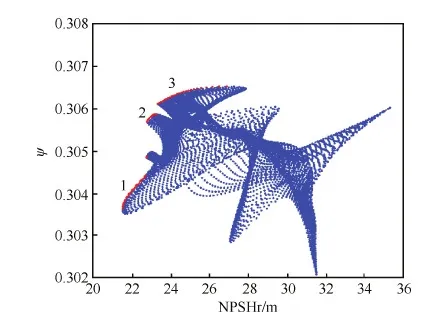
图8 目标变量分布Fig.8 Distribution of objectives

将Pareto最优解主要分为图示1、2、3区域，并给出其对应的自变量空间分布情况，如图9所示。本文主要关注于燃油泵的空化性能的研究，为此选取反映燃油泵空化性能的目标变量NPSHr取值较小的区域(1区域)作为进一步研究的自变量取值区域，表2给出了此区域内自变量的取值范围。

为了进一步研究自变量变化对目标变量的影响，分别固定自变量Δβb1和Δβb2(取固定值0)，通过数值计算得到目标变量随自变量的变化趋势，结果如图10和图11所示。从图10可以看到，在较大范围内NPSHr值不随Δβb1变化而变化，当Δβb1>4.4时，空化性能明显下降。由图11可知，当Δβb2增大时，NPSHr值先减小后增大，而Ψ值逐渐增大。综合以上分析，确定优化后燃油泵结构参数为Δβb1=4.4、Δβb2=3.2。

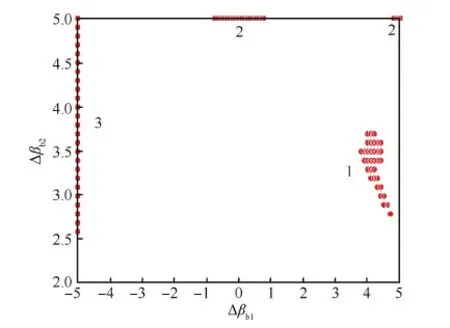
图9 Pareto最优解在自变量空间分布Fig.9 Distribution of Pareto optimal solution in variable space

表2 优化后自变量的取值范围Table 2 Value range of variables after optimization

VariableMaxMinΔβb14．73．8Δβb23．72．8

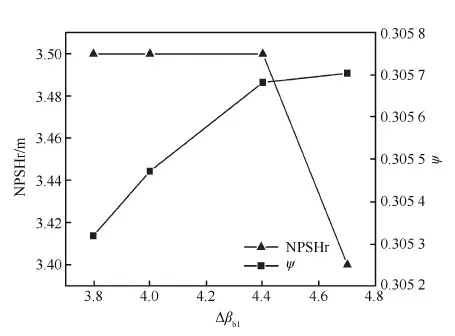
图10 目标变量随Δβb1变化趋势Fig.10 Variation of objectives with Δβb1

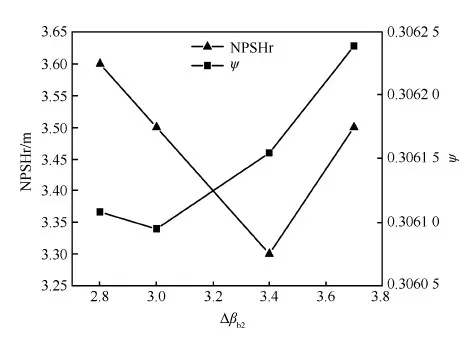
图11 目标变量随Δβb2变化趋势Fig.11 Variation of objectives with Δβb2

2.2.4 优化后燃油泵空化性能分析

图12给出了优化前后燃油泵空化性能曲线，从图中可以看出优化前后燃油泵空化性能曲线变化趋势相同，即随NPSHa的减小，扬程均先增大后减小；优化后的燃油泵必须空化余量较优化前减小了0.7 m(即18%左右)，燃油泵空化性能得到提高；同时，优化后燃油泵在无空化工况下的扬程较优化前仅减小0.05，燃油泵外特性基本保持不变。

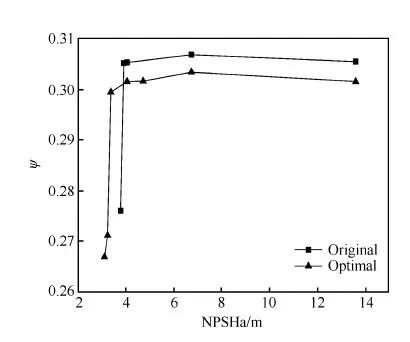
图12 优化前后燃油泵空化性能曲线Fig.12 Cavitation curves of original and optimal pump

图13给出了优化前后燃油泵在不同进口条件下诱导轮吸力面空泡分布及空泡面积Scavity。从图中可以看出，随着NPSHa的下降，诱导轮吸力面空泡区域开始产生空泡，并逐渐向后发展，空泡面积逐渐增大；在相同进口条件(即NPSHa相同)，优化后燃油泵诱导轮吸力面空泡面积比优化前分别减小了27%、15%、39%、10%，燃油泵空化性能得到显著提高。

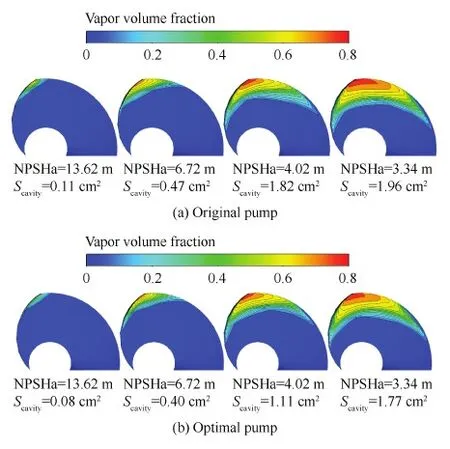
图13 优化前后诱导轮流道内空泡体积分布Fig.13 Cavity distributions of original and optimal pump in inducer

3 结 论

采用基于旋转修正的k-ε湍流模型对航空燃油泵的空化流动进行了数值计算，基于数值计算的结果，采用代理模型优化方法，对航空燃油泵的诱导轮和叶轮的结构参数进行了优化设计，得到以下结论：

1) 采用的数值计算方法能够准确地预测航空燃油泵的外特性与空化特性，通过分析得到，诱导轮出口安放角和叶轮入口安放角对燃油泵的空化性能和外特性影响较大。

2) 通过代理模型优化分析，燃油泵外特性和空化性能随诱导轮出口安放角和叶轮入口安放角的变化趋势为：燃油泵外特性随诱导轮和叶轮安放角的变化较小；叶轮出口安放角变化对燃油泵空化性能影响较大，随叶轮进口安放角的增大，燃油泵空化性能呈先减小后增大的变化趋势。

3) 当诱导轮出口安放角和叶轮进口安放角分别增大4.4° 和3.2° 时，满足Pareto最优解，此时燃油泵的空化性能较优化前提高了18%左右，在相同进口压力条件下，优化后燃油泵流道内空泡面积比优化前较小，空化性能更好。

[1] 樊思齐, 李华聪. 航空发动机控制[M]. 西安: 西北工业大学出版社, 2008.

FAN S Q, LI H C. Aeroengine control[M]. Xi’an: Northwestern Polytechnical University Press, 2008 (in Chinese).

[2] 薛梅新, 吴迪, 朴英. 加力燃油泵压出室非设计工况内流特征数值模拟[J]. 航空动力学报, 2012, 27(2): 419-424.

XUE X M, WU D, PIAO Y. Numerical simulation on internal flow characteristics in the discharge chamber of an afterburning fuel pump under off-design conditions[J]. Journal of Aerospace Power, 2012, 27(2): 419-424 (in Chinese).

[3] 殷吉超, 朴英, 彭晓峰. 高速燃油离心泵内流场分析和气蚀过程仿真[J]. 计算机仿真, 2008, 25(6): 70-74.

YIN J C, PIAO Y, PENG X F. Numerical simulation of flow field and cavitations in high-speed kerosene centrifugal pump[J]. Computer Simulation, 2008, 25(6): 70-74 (in Chinese).

[4] 王凯. 离心泵多工况水力设计和优化及其应用[D]. 镇江: 江苏大学, 2011.

WANG K. Multi-conditions hydraulic design and optimization for centrifugal pumps and its application[D]. Zhenjiang: Jiangsu University, 2011 (in Chinese).

[5] 何希杰. 离心泵叶轮入口参数最优化设计的研究[J]. 排灌机械工程学报, 1987, 5 (4): 18-25.

HE X J. Researching on optimization method for impeller inlet parameters of centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 1987, 5(4): 18-25 (in Chinese).

[6] 葛宰林, 吕斌, 于馨. 基于速度系数法的离心泵叶轮优化设计[J]. 大连铁道学院学报, 2006, 27(3): 37-40.

GE Z L, LV B, YU X. Optimal design of centrifugal pump impeller[J]. Journal of Dalian Railway Institute, 2006, 27(3): 37-40 (in Chinese).

[7] 高江永, 郭振苗. 离心泵叶轮与蜗壳设计几何参数的优化研究[J]. 水泵技术, 2007(4): 6-9.

GAO J Y, GUO Z M. Study on optimization of centrifugal pump impeller’s and volute’s designed parameters[J]. Pump Technology, 2007(4): 6-9 (in Chinese).

[8] SUANNE T, RUDOLF S. Optimization of hydraulic machinery bladings by multilevel CFD techniques[J]. International Journal of Rotating Machinery, 2005, 2(2): 161-167.

[9] 刘厚林， 王凯， 袁寿其, 等. 一种基于CFD的离心泵多工况水力优化方法: CN101956711A[P]. 2011-01-26.

LIU H L, WANG K, YUAN S Q, et al. A multi-conditions hydraulic optimization method for centrifugal pump based on CFD： CN101956711A[P]. 2011-01-26 (in Chinese).

[10] GOEL T, DORNEY D J, HAFTKA R T, et al. Improving the hydrodynamic performance of diffuser vanes via shape optimization[J]. Computer & Fluids, 2008, 37(6): 705-723.

[11] 杨卓懿, 庞永杰, 王建,等. 响应面模型在艇型多目标优化中的应用[J]. 哈尔滨工程大学学报, 2011, 32(4): 407-410.

YANG Z Y, PANG Y J, WANG J, et al. Application of a response surface model in multi-objective optimization for submersible shapes[J]. Journal of Harbin Engineering University, 2011, 32(4): 407-410 (in Chinese).

[12] 吴钦, 王国玉. 低温介质质量传输空化模型的代理分析及优化[J]. 应用力学学报, 2013,30 (5): 700-706.

WU Q, WANG G Y. Surrogate-based analysis and optimization of the transport-based cryogenic cavitation model[J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 700-706 (in Chinese).

[13] 赵宇, 王国玉, 黄彪. 考虑当地涡旋运动修正的湍流模型在非定常空化湍流流场计算中的应用[J]. 应用力学学报, 2014, 31(1): 1-6.

ZHAO Y, WANG G Y, HUANG B. Applications of LSC turbulence model on unsteady cavitating flows[J]. Chinese Journal of Applied Mechanics, 2014, 31(1): 1-6 (in Chinese).

[14] ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]//Proceedings of ICMF 2004 International Conference on Multiphase Flow. Yokohama, Japan: 2004: 1-11.

[15] 熊英华,刘影,李述林,等. 基于替代燃料的航空燃油泵内部空化特性[J].航空动力学报,2015,30(11):2607-2615.

XIONG Y H, LIU Y, LI S L, et al. Cavitation characteristic in aviation fuel pump based on surrogate fuel[J]. Journal of Aerospace Power, 2015,30(11):2607-2615 (in Chinese).

[16] 关醒凡. 泵的理论与设计[M]. 北京: 机械工业出版社, 1987.

GUAN X F. Pumps theory and design[M]. Beijing: China Machine Press, 1987 (in Chinese).

[17] QUEIPO N V, HAFTKA R T, SHYY W, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences, 2005, 41: 1-28.

[18] MACK Y, GOEL T, SHYY W, et al. Surrogate model-based optimization framework: A case study in aerospace design[J]. Studies in Computational Intelligence, 2007, 51: 323-342.

[19] BASAK D, PAL S, PATRANABIS D C. Support vector regression[J]. Neural Information Processing Letters & Reviews, 2007, 11(10): 203-224.

[20] GOEL T, HAFTKA R T, SHYY W, et al. Ensemble of surrogates[J]. Structure and Multidiscipline Optimization, 2007, 33(3): 199-216.

[21] CHO Y C, DU W, GUPTA A, et al. Surrogate-based modeling and dimension-reduction techniques for thermo-fluid and energy systems[C]//ASME/JSME 2011 8th Thermal Engineering Joint Conference. American Society of Mechanical Engineers.New York:ASME, 2011:1-19.

熊英华男， 硕士， 研究员。主要研究方向： 燃油泵空化流动。

Tel.: 010-68912395

E-mail: xiongyhbit@163.com

刘影女， 副教授。主要研究方向： 流体机械空化流动。

Tel.: 010-68912395

E-mail: liuying@bit.edu.cn

URL：www.cnki.net/kcms/detail/11.1929.V.20160411.1043.002.html

Analysisofcavitationperformanceofanaviationfuelpumpbasedonsurrogatemodel

XIONGYinghua1,LIUYing1,*,ZHAOXing’an1,SUNHuawei2,WANGGuoyu1,GAODeming1

1.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081,China2.NanjingElectricalandHydraulicEngineeringResearshCenter,AviationIndustryCorporationofChina,Nanjing211106,China

Inordertoinvestigatetheinfluenceofthestructureparameters(whicharebladeangleofinduceratexitandbladeangleofimpelleratinlet)offuelpumponthecavitationperformanceofanaviationfuelpump,theglobalsensitivityanalysismethodthatbasedonthesurrogatemethodwasapplied,andalso,thestructureparametersoffuelpumphadbeenoptimized.Inthenumericalsimulation,thelocalswirlingcorrectionturbulencemodelderivingfromthestandardk-εtwo-equationmodelandZwartcavitationmodelwereapplied.Theresultsshowthatinacertainrangeofvariation,thebladeanglehasagreaterinfluenceonthecavitationperformance,insteadoftheexternalcharacteristicsoffuelpump.Comparedtotheoutletangleofinducer,theinletangleofimpelleraffectsthecavitationperformancemoresignificantly.Withtheincreaseoftheoutletangleofinducer,thecavitationperformancefirstlydecreasesandthenincreases.BasedontheParetooptimalsolutions,theoptimizedoutletangleofinducerandinletangleofimpellerincreaseby4.4°and3.2°respectively,withthecavitationperformanceincreasingby18%.

fuelpumps;surrogatemodel;turbulencemodel;cavitationperformance;analysisandoptimization

2015-10-12；Revised2015-12-14；Accepted2016-03-28；Publishedonline2016-04-111043

s：NationalNaturalScienceFoundationofChina(51479002);AeronauticalScienceFoundationofChina(2013ZC09001)

.Tel.：010-68912395E-mailliuying@bit.edu.cn

2015-10-12；退修日期2015-12-14；录用日期2016-03-28； < class="emphasis_bold">网络出版时间

时间：2016-04-111043

www.cnki.net/kcms/detail/11.1929.V.20160411.1043.002.html

国家自然科学基金 (51479002)； 航空科学基金 (2013ZC09001)

.Tel.：010-68912395E-mailliuying@bit.edu.cn

熊英华， 刘影， 赵兴安， 等．基于代理模型的航空燃油泵空化性能分析J．航空学报,2016,37(10):2952-2960.XIONGYH,LIUY,ZHAOXA,etal.AnalysisofcavitationperformanceofanaviationfuelpumpbasedonsurrogatemodelJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2952-2960.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0102

V288.1+4； O359.1

A

1000-6893(2016)10-2952-09