基于应变能与模糊贴近度的拱坝体形稳健优化设计
闫超君,孙林松
(1.安徽水利水电职业技术学院,安徽合肥231603;2.扬州大学水利与能源动力工程学院,江苏扬州225009)
基于应变能与模糊贴近度的拱坝体形稳健优化设计
闫超君1,孙林松2
(1.安徽水利水电职业技术学院,安徽合肥231603;2.扬州大学水利与能源动力工程学院,江苏扬州225009)
在拱坝体形优化设计时,以坝体应变能及其对基岩变形模量的灵敏度为目标函数,建立了拱坝体形稳健优化设计模型。具体求解时,首先对各分目标进行单目标优化,得到理想解,然后通过构造目标函数向量与理想解目标向量的模糊贴近度,将稳健优化模型转化为求最大模糊贴近度的单目标优化问题。结合某拟建拱坝的工程算例表明,相比于线性加权法,模糊贴近度法的优化结果更靠近理想解,坝体的应力状态更优。
应变能;模糊贴近度;稳健优化;拱坝
拱坝体形优化设计研究最早可追溯至20世纪60年代末期,我国在这方面的研究虽然起步比国外晚了10年,但是由于我国的拱坝体形设计紧密结合工程实际开展研究工作,现在已领先于国际水平[1]。文献[2]对拱坝优化的研究现状进行了总结,初期的拱坝体形优化研究是以节省工程造价为目标进行的,随着高拱坝建设的发展,人们更加重视拱坝的安全性,在拱坝体形优化研究中又提出了各种拱坝优___化安全性模型[3-5]以及综合考虑安全性和经济性的多目标优化模型[6-8]。谢能刚等[9]在综合分析了常用的拱坝安全性指标后,提出了以应变能作为安全性目标函数的拱坝体形优化模型。
现有的拱坝体形优化设计通常是在特定的条件下进行的。但是,这些设计条件往往存在一定的不确定性,如溪洛渡、小湾等拱坝在施工开挖后均发现实际地质条件与设计时有一定的差别,所以在拱坝体形优化设计时应考虑地质、施工等因素的不确定性。文献[10]在优化过程中考虑坝体自重荷载分步施加,以期更符合工程实际。文献[11]利用稳健设计的思想,在拱坝体形优化设计中引入稳健可行性约束,建立了基于基岩变形模量不确定性的拱坝稳健可行性优化设计模型。本文拟以坝体应变能为优化目标函数,进一步考虑目标函数的稳健性,建立基于应变能的拱坝体形稳健优化设计模型,采用模糊贴近度将其转化为单目标问题,并结合某拟建拱坝进行分析。
1 基于应变能的拱坝体形稳健优化模型
通常情况下,拱坝体形优化设计的数学模型可表示为:

其中,xi(i=1,2,…,n)为由拱坝体形参数构成的设计变量;F(X)为目标函数为坝体最大有限元等效拉应力及其容许值为坝体最大有限元等效压应力及其容许值;φmax及[φmax]为拱圈最大中心角及其容许值;gj(X)(j= 1,2,…,p)为其它几何约束,如界限约束、保凸约束等。
稳健优化设计一般包含约束可行性的稳健性和目标函数的稳健性两个方面[11]。约束可行性的稳健性要求当设计因素发生变化时,设计方案仍然能满足约束条件的要求。本文采用文献[11]中基于最大波动分析的稳健可行性约束,即将式(1)中的应力约束改为

式中:E=[E1E2…Em]T为坝基岩体变形模量。
目标函数的稳健性即目标函数对设计因素的不敏感性,可用其对不确定设计因素的灵敏度的绝对值来描述[12],灵敏度的绝对值越小说明目标函数对该设计因素越不敏感,即稳健性越好。当目标函数为坝体应变能Π,不确定设计因素为岩体变形模量Ei(i=1,2,…,m)时越小,目标函数的稳健性越好。
综合以上分析,坝基岩体变形模量不确定条件下基于坝体应变能的拱坝体形稳健优化模型可概括为:
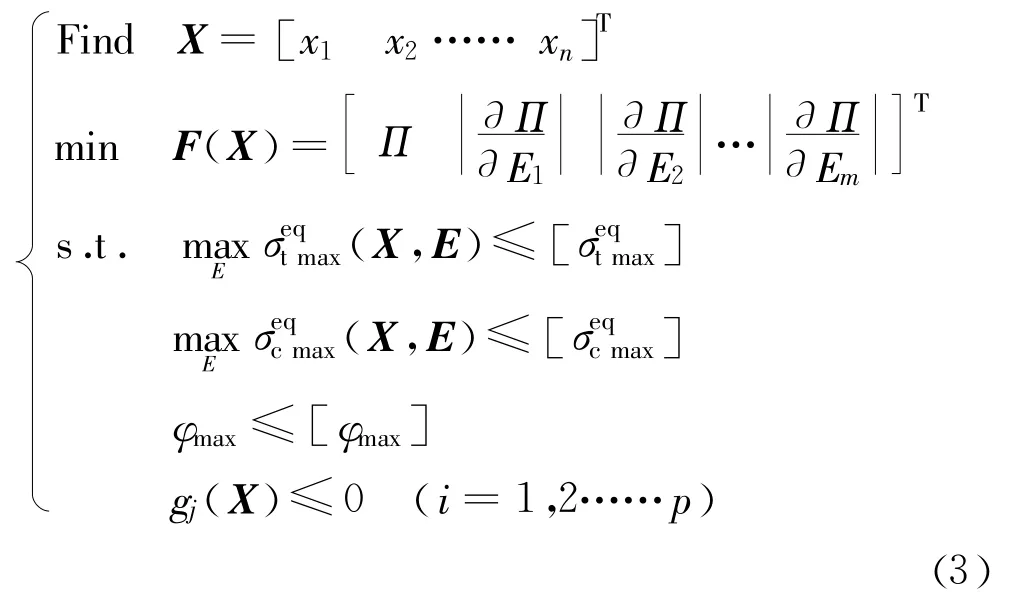
式中:Π为坝体应变能;mEax(X,E)和max E(X,E)分别为坝基岩体变形模量不确定条件下的最大等效压应力和最大等效拉应力,具体计算方法参见文献[13];E=[E1E2…Em]T为坝基岩体变形模量。
2 多目标优化的模糊贴近度解法
稳健优化设计模型式(3)是一个多目标优化问题,为叙述方便,写成以下一般形式:

若存在X*,使各个分目标Fi都达到其最小值,则称X*为理想解为理想目标向量。由于各分目标之间的排斥性,理想解一般是不存在的,通常希望获得一个最接近理想解的最优解。这可以采用模糊贴近度的概念来求解。
对解X,设与之相应的目标向量为F=[F1F2…F1]T,构造各分目标Fi相对于其最小值F*i的隶属度μi:

式中:Fimax为分目标Fi的允许最大值,可参照分目标优化的结果确定。
解X对应的目标函数向量模糊子集为~F=[μ1μ2…μl]T,显然,理想目标向量的模糊子集为的贴近程度可用模糊贴近度来表征,其值越大表示两者越接近。本文采用如下距离贴近度[14]:

这样,多目标优化问题就转化为如下单目标优化问题
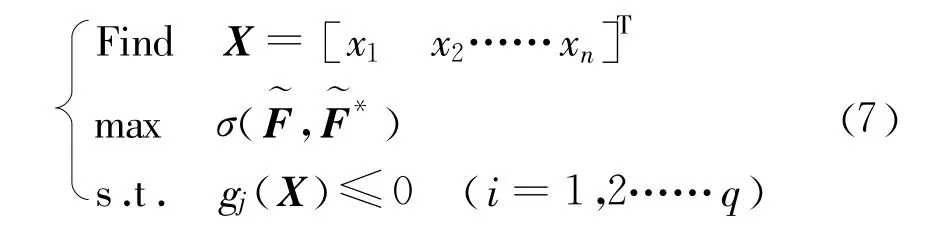
3 工程算例
3.1 基本资料
某拟建拱坝,最大坝高289.0 m,坝顶高程834.0 m,该坝体形拟选椭圆体形。该坝基主要为P2β3-P2β6段玄武岩,以变玄武质角砾熔岩、微晶隐晶玄武岩及杏仁状玄武岩为主,岩体较坚硬,部分岩性段柱状节理发育,主要出露于坝基中下部(包括河床坝基),其变形模量较低。此岩体概括为3类,坝基岩体分区及变形参数见表1。

表1 坝基岩体分区及变形参数
考虑岩体性质的不同,三类岩体的变形模量E1、E2、E3之间应满足下列关系
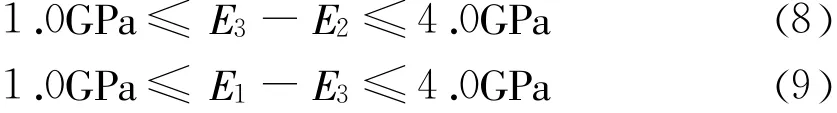
3.2 优化模型
在优化设计中,本文取的设计变量为4个控制高程处的拱冠梁与拱圈体形参数,共31个,具体分布、取值区间见表2。
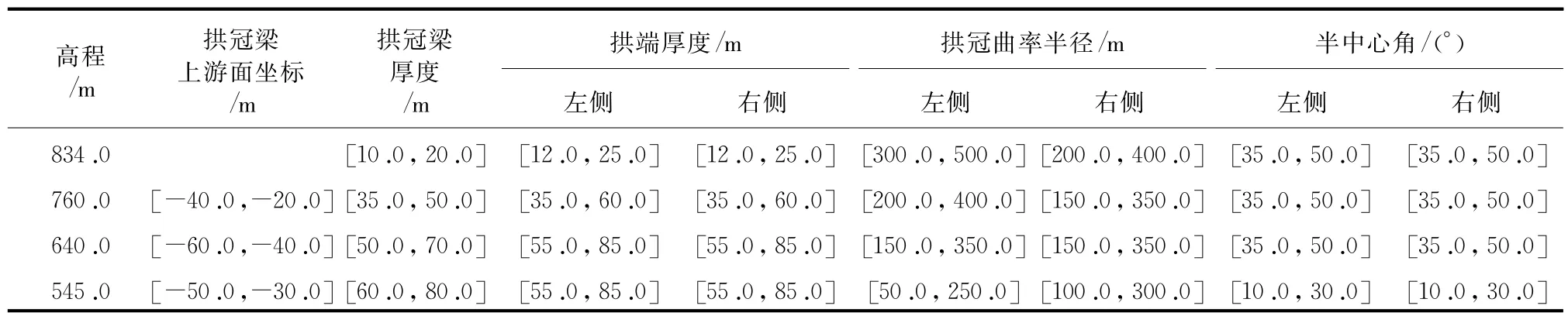
表2 设计变量分布及取值区间

表3 单目标优化设计的各分目标比较
3.3 优化方法
考虑式(3)中各分目标进行单目标优化,与各优化设计方案相应的分目标函数值如表3所示,可见,理想目标向量F*=[3.7438 0.2422 0.1831 0.0795]T,各分目标的允许最大值分别取4.1401 GJ、0.2966 J/Pa,0.2209 J/Pa和0.0938 J/Pa。这样,不难按照式(3)及式(5)~式(7)建立基于模糊贴近度的拱坝应变能稳健优化模型。优化方法采用文献[15]提出的加速微种群遗传算法,表4给出了优化方案的体形参数。

表4 应变能稳健优化设计拱坝体形参数
图1和表5分别给出了不同设计方案的拱冠剖面形状与体形特征参数,其中线性加权法优化方案各分目标取相同的权系数。表6对比了不同设计方案的拱坝主要性能指标,其中分别为设计基岩变形模量条件下的坝体应变能及其对基岩变形模量的灵敏度;σtmax、σcmax和分别为坝体最大主拉应力、主压应力与最大有限元等效主拉应力、主压应力分别为基于基岩变形模量不确定性时的坝体最大有限元等效主拉应力和等效主压应力。

图1 拱冠剖面对比

表5 不同设计方案的体形特征参数对比

表6 不同设计方案的主要性能指标对比
4 结 论
本文以坝体应变能及其对基岩变形模量的灵敏度为目标函数,同时考虑应力约束的稳健可行性,建立了基于应变能的拱坝稳健优化模型;并通过构造目标函数向量与理想解目标向量的模糊贴近度,将其转化为单目标优化问题求解。对某拟建拱坝的优化计算表明,相对于线性加权法,本文方法优化结果更接近理想解,坝体应力状态更优。
[1] 朱伯芳,厉易生.高拱坝新型合理体形的研究和应用[J].水力发电,2001(8):60-62.
[2] 陈知渊.拱坝及其优化方法的发展现状与展望[J].水利与建筑工程学报,2006,4(4):91-93,97.
[3] 孙林松,王德信,裴开国.以应力为目标的拱坝体型优化设计[J].河海大学学报,2000,28(1):57-60.
[4] 陈知渊.以坝肩稳定安全系数为目标的高拱坝优化设计[D].南京:河海大学,2007.
[5] 张 鹏.基于整体稳定安全度为目标函数的高拱坝优化设计[J].广东水利水电,2011(7):78-81.
[6] 孙文俊,孙林松,王德信,等.拱坝体形的两目标优化设计[J].河海大学学报,2000,28(3):39-43.
[7] 汪树玉,刘国华,杜王盖,等.拱坝多目标优化研究与应用[J].水利学报,2001,32(10):48-52.
[8] 谢能刚,孙林松,王德信.静力与动力荷载下高拱坝体型多目标优化设计[J].水利学报,2001,32(10):8-11.
[9] 谢能刚,孙林松,赵 雷,等.基于应变能的拱坝体型优化设计[J].水利学报,2006,37(11):1342-1347.
[10] 何华志,李 琼,刘 莹.基于生死单元原理的拱坝体形优化[J].水利与建筑工程学报,2012,10(5):155-157.
[11] 孙林松,孔德志.基础变形模量不确定条件下的拱坝体形稳健可行性优化设计[J].水利水电科技进展,2014,34(1):61-64,77.
[12] 陈立周.稳健设计[M].北京:机械工业出版社,2000.
[13] 孙林松,孔德志.基础变形模量不确定条件下的拱坝最大有限元等效应力分析[J].河海大学学报(自然科学版),2012,40(5):530-533.
[14] 谢季坚,刘承平.模糊数学方法及其应用[M].4版.武汉:华中科技大学出版社,2015.
[15] 孙林松,张伟华.加速微种群遗传算法及其在结构优化设计中的应用[J].应用基础与工程科学学报,2008,16(5):741-748.
Robust Shape Optimization Design for Arch Dams Based on Strain Energy and Fuzzy Nearness
YAN Chaojun1,SUN Linsong2
(1.Anhui Water Conservancy Technical College,Hefei,Anhui 231603,China;2.College of Hydraulic,Energy&Power Engineering,Yangzhou University,Yangzhou,Jiangsu 225009,China)
In the optimization shape design of arch dam,a robust optimization model for shape design of arch dams based on strain energy was proposed,in which strain energy of dam body and its sensitivity to the deformation modulus of foundation considered as objective functions and robust feasibility constraint of stress was adopted.In the solution process,firstly,utopia solution was obtained by single-objective optimizing of each objective function.Secondly,a fuzzy nearness between a solution and utopia solution is constructed.Finally,robust feasibility optimization model is transformed to a single-objective optimization problem to maximize the fuzzy nearness.The calculation of a planned arch dam indicates that compared to the solution of linear weighted sum method,the optimal design of fuzzy nearness method is closer to utopia solution and with better dam stress state.
strain energy;fuzzy nearness;robust optimization;arch dam
TV624.4
A
1672—1144(2016)05—0037—04
10.3969/j.issn.1672-1144.2016.05.007
2016-05-27
2016-06-25
国家自然科学基金项目(51279174)
闫超君(1967—),女,河南焦作人,硕士,副教授,高级工程师,主要从事水利水电工程的教学与研究。E-mail:575649021@qq.com
孙林松(1968—),男,江苏姜堰人,博士,教授,主要从事结构现代设计理论与分析方法研究。E-mail:linsong-sun@126.com

