国内外不同规范对弯剪破坏钢筋混凝土墩柱的受剪承载力计算比较

石程程，马 颖，罗国杰，许新勇

（华北水利水电大学水利学院，河南郑州450045）

国内外不同规范对弯剪破坏钢筋混凝土墩柱的受剪承载力计算比较

石程程，马 颖，罗国杰，许新勇

（华北水利水电大学水利学院，河南郑州450045）

弯剪破坏作为地震作用下会发生的一种破坏方式，破坏过程较为复杂，各国对塑性铰区域受剪承载的研究也相对较少，针对此问题，借助美国PEER柱抗震性能试验数据库，统计分析了其中16根矩形截面发生弯剪破坏的拟静力试验墩柱的数据，对我国水利行业标准《水工混凝土结构设计规范》（SL/ T191-96）、《水工混凝土结构设计规范》（SL191-2008）、电力行业标准《水工混凝土结构设计规范》（DL/ T5057-2009）及中国《混凝土结构设计规范》（GB50010-2010）中受剪承载力设计的可靠性进行了评价，并与欧、美相关设计规范进行对比分析。研究表明，轴压比在0.1～0.3之间的弯剪破坏墩柱，规范基本可满足承载力要求；而轴压比小于0.1或大于0.3的墩柱，在抗震设计时应予以注意。

钢筋混凝土；墩柱；地震荷载；弯剪破坏；抗剪承载力

作为水电站厂房、泵站厂房、渡槽、桥梁等结构的重要竖向承重构件，钢筋混凝土柱、墩在地震作用下极易发生破坏。我国是地震多发国家，尤其西南地区更是地震高发区，也是我国的水电开发中心，从抗震防灾的角度考虑，如果闸墩、水电站厂房支撑柱等柱类构件破坏严重且难以修复，则会造成巨大的灾害与损失［1］。通常，钢筋混凝土柱在地震作用下有弯曲、弯剪和剪切三种破坏方式［2］。其中，弯曲破坏能够吸取较大的地震能量，为延性破坏；剪切破坏是伴随强度与刚度迅速下降的脆性破坏，设计中应予以避免；弯剪破坏介于弯曲破坏与剪切破坏之间，随着变形增大，受剪承载力逐渐减小，最终因受剪承载力不足发生脆性破坏，设计中应保证弯剪破坏时具有一定满足要求的塑性变形能力［3］。因此，柱在剪切破坏和弯剪破坏方式下受剪承载力的研究十分重要。而柱受剪承载力的计算方法大多是基于剪切破坏建立的，各国对其都有较多的研究，也都有相应规范规定，并且大多为经验公式。但柱弯剪破坏的破坏过程较为复杂，关于塑性铰区域受剪承载力，各国的研究相对较少。

本文以发生弯剪破坏的柱为研究对象，统计分析了PEER柱抗震性能试验数据库中弯剪破坏试件的16组试验数据，对中国水利行业标准《水工混凝土结构设计规范》［4］（SL/T191-96）、《水工混凝土结构设计规范》［5］（SL191-2008）、中国电力行业标准《水工混凝土结构设计规范》［6］（DL/T5057-2009）、中国《混凝土结构设计规范》［7］（GB50010-2010）中受剪承载力设计的可靠性进行了评价，并与欧洲《结构抗震设计规范》［8］（1998-2：1996）、新西兰桥梁标准（1995）［9］、加利福尼亚《抗震设计准则》［10］（1999）、ATC/MCEER［11］（地震工程研究多科学中心）及日本《公路桥梁设计规范》［12］（1996）设计规范对比分析。

1 国内外规范受剪承载力设计模型

对于钢筋混凝土柱受剪承载力，通常按下面的表达式计算：

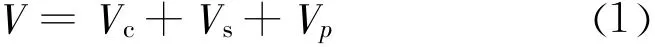
式中：Vc为混凝土承担的受剪承载力；Vs为箍筋承担的部分；Vp为轴力对受剪承载力的作用部分。Vs计算公式通常是采用不同角度的桁架模型计算［13］的，不同规范规定的较为相似；但在考虑Vc和Vp的影响方面，差别很大，考虑的因素有所不同［14］。

中国水利行业“96”水工设计规范与“08”水工设计规范所规定的受剪承载力都是由混凝土、箍筋以及轴向压力三部分的贡献组成，只是“08”规范在计算Vc时考虑的是轴心抗拉强度；中国电力行业“09”水工设计规范与水利行业“08”水工设计规范相似，所规定的受剪承载力也是由三部分构成，只是安全系数的定义略有差别；中国建筑行业“10”结构设计规范所规定的受剪承载力也是由三部分构成，在计算Vc考虑了剪跨比的影响。

欧洲“96”抗震设计规范规定的受剪承载力包括两部分，即考虑轴力作用下混凝土提供的受剪承载力Vc和箍筋承担的剪力部分Vs；新西兰“95”桥梁标准是基于45°的桁架模型建立公式的，在确定塑性铰区域的Vc时，考虑了纵向钢筋配筋量和轴向荷载的影响，轴向荷载的影响只用于轴压比大于0.1的情况；加利福尼亚“99”抗震设计准则考虑位移延性系数对Vc的影响，并基于45°桁架模型计算Vs；ATC/MCEER（地震工程研究多科学中心）根据NCHRP［15］的研究成果，考虑边界条件系数，为AASHTO-LRFD［16］抗震设计指南建议的钢筋混凝土柱受剪承载力计算公式也是由以上三部分的贡献组成；日本“96”公路桥梁规范与以上规范不同，考虑了混凝土抗剪强度与混凝土受压区高度等因素，规定受剪承载力计算模型包括混凝土与横向钢筋两部分。

2 弯剪破坏墩柱试件试验数据及抗剪能力识别

2.1 试验数据

由前面的计算模型可以看出，每个规范的模型还是有很大差别的，尤其是我国规范与美国和欧洲规范之间。为了对比分析以上模型的受剪承载力计算结果与真实破坏值的差别，本文收集了PEER柱抗震性能试验数据库中的16根钢筋混凝土柱矩形截面柱的试验数据，表1为试验柱的基本参数。基于以上9种规范模型，试对各规范受剪承载力计算方法的可靠性进行评价。

由于中国、美国和欧洲采用的混凝土强度标准试件不同，定量对比时需进行换算，分别按下式将美

式中：δfcu为试件抗压强度的变异系数。

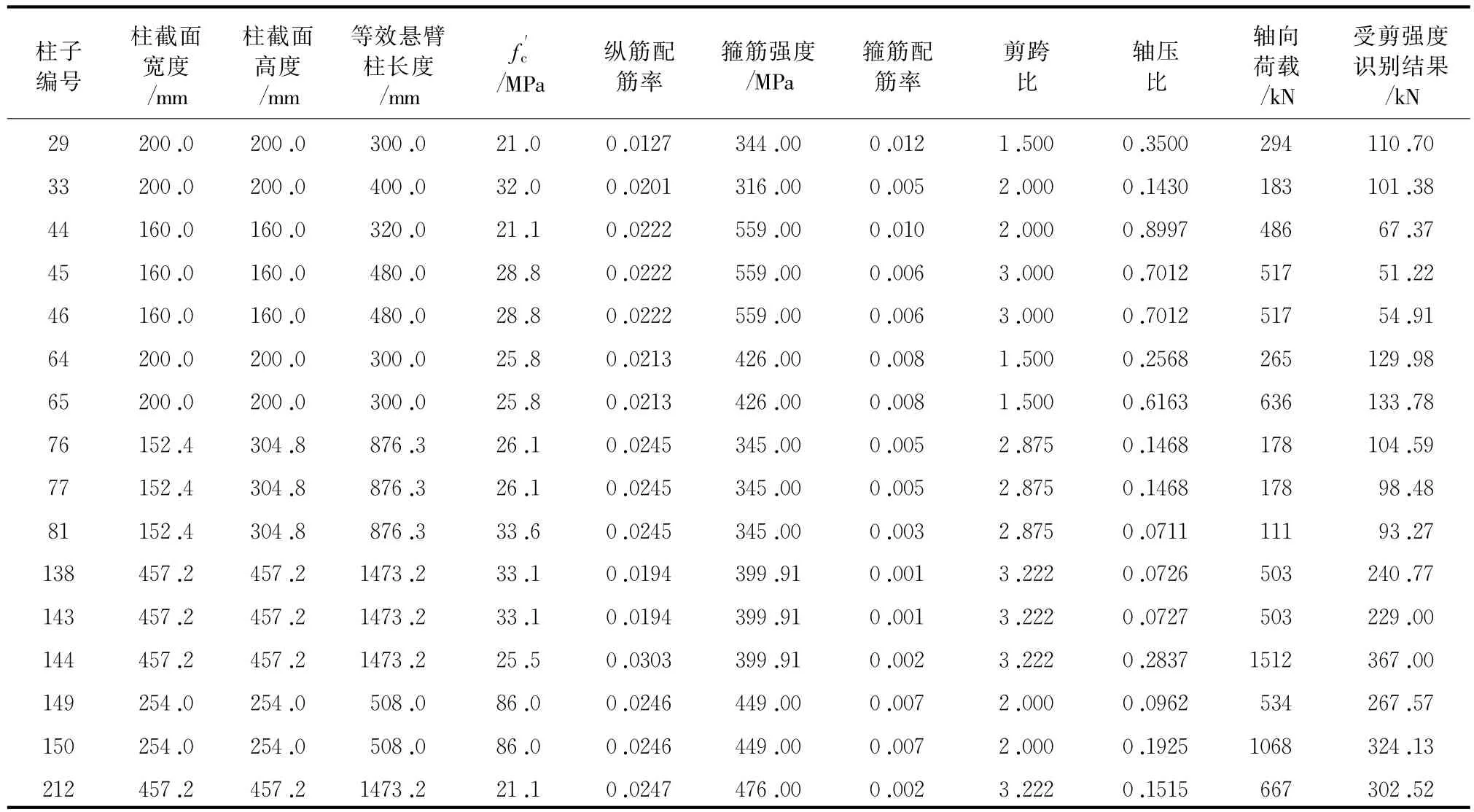
表1 试验柱的基本参数及受剪强度识别结果

2.2 弯剪破坏墩柱试件受剪承载力

PEER柱试验数据库只有破坏方式分类及荷载—位移滞回曲线数据，因此需要识别发生弯剪破坏试件的最终受剪强度，本文对弯剪破坏试件受剪承载力的识别采用了文献［18］中的方法：钢筋混凝土墩柱弯曲屈服后，反复施加幅值为δ的同一位移，若其末次水平荷载（通常循环次数大于等于3）小于同幅值位移下最大荷载值的85%时，即Fδ，end≤0.85Fδ，max则以第一次施加幅值为δ的位移所对应的水平荷载（最大荷载）为弯剪破坏墩柱试件的受剪强度，识别结果见表1。

3 分析评价

将发生弯剪破坏的试验柱的实际破坏值与我国水利行业“96”水工设计规范、“08”水工设计规范、我国电力行业“09”水工设计规范、建筑行业“10”结构设计规范、欧洲“96”抗震设计规范、新西兰“95”桥梁标准、加利福尼亚“99”抗震设计准则、ATC/MCEER及日本“96”公路桥梁设计规范所规定的模型计算值进行对比分析，以评价各规范中剪力计算模型对保证钢筋混凝土柱、墩不发生弯剪破坏的可靠性。

按计算值与实测值将各个试件予以区分，将计算值等于实测值为界限分为两个区域。当实测值大于规范计算值，说明规范的保守性；当实测值小于规范计算值，表明试件在未到达规范要求时就发生了弯剪破坏，说明了规范的危险性，见图1。将出现在图1中右下方即不安全区域的试件数除以总试件数16即得出基于以上16组试件各规范失效的概率，见图2。将试件受剪承载力各规范计算值与实测值作比较，得出误差，并依照统计学算出误差的均值与标准差，以衡量各规范计算值的精度，见表2。

（1）对于我国水利行业标准《水工混凝土结构设计规范》［4］（SL/T191-96），由图1（a）知轴压比在0.1～0.3之间的试件中多数出现在左上区域，即安全区域，本文选用的试件中轴压比在此范围内的共有7组，其中6组都分布在此区域内。还有大部分试件出现在右下部分，即不安全部分，尤其是轴压比大于0.3的试件表现更为明显，轴压比大于0.3的5组试件均出现在不安全区域，轴压比小于0.1的4组试件也有1组出现在不安全区域。由表2可知计算误差的标准差为56.84 kN，说明计算值与实测数据离散较大，另外由图2知我国该规范的失效概率高达43.75%。

（2）对于我国水利行业标准《水工混凝土结构设计规范》［5］（SL191-2008），由图1（b）知部分试件出现在分界处，即实测数据与计算值比较相近，特别是轴压比在0.1～0.3之间的试件表现较为明显，轴压比在此范围内的7组试件中有6组都分布在分界处。另外还有大部分试件出现在右下部分，即不安全部分，尤其是轴压比大于0.3与轴压比小于0.1的试件表现更为明显，轴压比大于0.3的5组试件均出现在不安全区域，轴压比小于0.1的4组试件也有3组出现在不安全区域。由表2可看出，与“96”规范相比“08”规范计算误差的标准差较低，仅为29.36 kN，说明“08”规范的精准程度较“96”规范有很大提高。由图2知我国该规范的失效概率高达56.25%。

图1 各规范的抗剪强度计算值与实测值的比较

（3）对于我国电力行业标准《水工混凝土结构设计规范》［6］（DL/T5057-2009），由图1（c）知试件分布情况与我国水利行业标准08规范的试件分布情况相似，计算值与实测数据较为接近，由表2知计算误差的标准差仅为28.98 kN。另外出现在不安全区域的试件比例有所下降，由图2知失效概率为43.75%，但试件出现在不安全区域的数量依然较高且多数仍表现为轴压比大于0.3与轴压比小于0.1的试件，轴压比大于0.3的5组试件中有4组出现在不安全区域，轴压比小于0.1的4组试件也有3组出现在不安全区域。

（4）对于我国建筑行业《混凝土结构设计规范》［7］（GB 50010-2010），由图1（d）知试件分布情况与我国水利行业与电力行业标准的《水工混凝土结构设计规范》［4-6］试件分布类似，其中5组轴压比大于0.3的试件均出现在不安全区域，而对于轴压比小于0.3的试件大都表现出较好的安全性。由表2知计算误差的标准差为37.21 kN，离散程度较低，计算值与实测值较接近。另外仍有大部分试件出现在不安全区域，由图2知失效概率为43.75%。

（5）综合比较所有规范，抗剪承载力模型对于保证钢筋混凝土柱不发生弯剪破坏方面，欧洲《结构抗震设计规范》［8］最为可靠，大部分试件出现在安全区域，出现在不安全区域的试件全部表现为轴压比大于0.3的5组试件中的4组（图1（e）），由图2知失效概率仅为25%。但由表2可知，计算误差的标准差为86.01 kN，计算值与实测值的离散程度较大。

（6）对于新西兰桥梁标准［9］（1995），该模型只适用于轴压比大于0.1的试件，由图1（f）知出现在不安全区域的试件中包括轴压比大于0.3的全部试件与1组轴压比在0.2与0.3之间的试件，而对于轴压比小于0.2的5组试件均出现于分界线处，表现较安全。另外，由表2数据知该规范的计算误差较大。

（7）对于加利福尼亚《抗震设计准则》（1999）和ATC/MCEER规范，由图1（g）、图1（h）知分布情况较为相似，仍然有大部分试件出现在不安全区域，由表2数据知计算值与实测值的离散性也比较大。由图2知失效概率分别为56.25%和50%，其中轴压比大于0.3的试件全部出现于不安全区域，轴压比在0.1与0.3之间的7组试件中均有4组出现于不安全区域，而轴压比小于0.1的4组试件中仅有1组不安全，表现出较高的安全性。

（8）对于日本规范，由图1（i）知，大部分试件出现在分界处，由表2知计算值与实测值差的标准差为57.10 kN，离散程度略高。由图2知失效概率为31.25%，仅次于欧洲规范。与其他规范不同的是，日本规范对于轴压比大于0.3的试件表现较为安全，5组试件均出现在安全区域，而对于轴压比小于0.1的4组试件全部出现在不安全区域。

（9）值得注意的是，国内外学者［19］很多认为混凝土的抗剪承载力与位移延性系数μΔ二者关系密切，即抗剪承载力随着位移延性系数μΔ增大而减小，然而只有加利福尼亚《抗震设计准则》（1999）反映了这一规律。

图2 各规范的失效概率

表2 计算值与实测值差的均值与标准差

4 结 语

本文选取了PEER柱抗震性能试验数据库中的弯剪破坏试件，对我国水利行业“96”水工设计规范、“08”水工设计规范、我国电力行业“09”水工设计规范、建筑行业“10”结构设计规范、欧洲“96”抗震设计规范、新西兰“95”桥梁标准、加利福尼亚“99”抗震设计准则、ATC/MCEER及日本“96”公路桥梁设计规范中受剪承载力模型对保证钢筋混凝土柱、墩不发生弯剪破坏的可靠性。研究得到如下结论：

（1）我国水利行业“96”水工设计规范、“08”水工设计规范中的受剪承载力计算模型偏于不安全，电力行业“09”水工设计规范及建筑行业“10”结构设计规范中的受剪承载力计算模型也略偏于不安全，尤其对于高轴压比试件尤甚，不能用于计算发生弯剪破坏的钢筋混凝土柱、墩。

（2）外国规范中欧洲“96”抗震设计规范最为可靠，可以用于计算发生弯剪破坏的钢筋混凝土柱墩；日本规范对高轴压比试件较为可靠；而新西兰“96”桥梁标准、加利福尼亚“99”抗震设计准则和ATC/ MCEER中的受剪承载力计算模型对于弯剪破坏试件偏于不安全。

总体上看我国规范在弯剪破坏方面的计算结果大都偏于不安全，不如欧洲规范安全。本文对水利工程中已建柱类构件的抗剪能力进行了简要的总结，汶川地震前已建桥墩是依据“96”规范设计的，轴压比小于0.3的柱墩基本可满足承载力要求；汶川地震后按“08”规范设计墩柱，轴压比小于0.1或大于0.3的情况应在柱类构件的抗震设计中予以注意。

［1］ 李富荣.水-桩-土-桥墩结构体系的地震反应分析［J］.水利与建筑工程学报，2008，6（2）：47－49.

［2］ 马 颖.钢筋混凝土柱地震破坏方式及性能研究［D］.大连：大连理工大学，2012：7－10.

［3］ 马 颖，张 勤，贡金鑫.钢筋混凝土柱弯剪破坏恢复力模型骨架曲线［J］.建筑结构学报，2012，33（10）：116－125.

［4］ 中华人民共和国水利部.水工混凝土结构设计规范：SL/T191-96［S］.北京：中国水利水电出版社，1996.

［5］ 中华人民共和国水利部.水工混凝土结构设计规范：SL191-2008［S］.北京：中国水利水电出版社，2008.

［6］ 中华人民共和国电力部.水工混凝土结构设计规范：DL/T5057-2009［S］.北京：中国电力出版社，2009.

［7］ 中华人民共和国建设部.混凝土结构设计规范：GB 50010—2010［S］.北京：中国建筑工业出版社，2011.

［8］ European Committee for Standardization.Eurocode 8 Design of Structures for Earthquake Resistance－Part 2：Bridges［S］. Brussels：European Committee for Standardization，1998.

［9］ Transit New Zealand.New Zealand Standard-1995，Bridges and Structures Design Manual-Metric［S］.Wellington：Transit New Zealand，1995.

［10］ California Department of Transportation.Seismic Design Criteria［S］.Version 1.1.Sacramento：California Department of Transportation，1999.

［11］ Capron M R，Friedland I M，Mayes R L.Seismic Design of Highway Bridges：Recommended Specifications［C］//Structures 2001：A Structural Engineering Odyssey ASCE，2013：1－1.

［12］ Japan Road Association.Specifications for highway bridge，Part V：Seismic Design［S］.Tokyo：Maruzen Publishing Co.，Ltd.，1996.

［13］ 管品武，王 博，徐泽晶.钢筋混凝土构件抗剪承载力分析方法比较［J］.世界地震工程，2002，18（3）：95－101.［14］ 苏 征.混凝土本构模型的选用对RC柱非线性分析的影响［J］.水利与建筑工程学报，2012，10（4）：174－177.

［15］ Hawkins N M，Kuchma D A，Mast R F，et al.NCHRP web－only document 78：simplified shear design of structural concrete members：Appendixes［R］.［s.l］：［s.n］，2006：78－80.

［16］ AASHTO.AASHTO LRFD Bridge Design Specifications［S］.4th Edition.Washington，D.C：American Association of State Highway and Transportation Officials，2007.

［17］ 贡金鑫，魏巍巍，胡加顺.中美欧混凝土结构设计［M］.北京：中国建筑工业出版社，2007：77－79.

［18］ 王东升，司炳君，孙治国，等.地震作用下钢筋混凝土桥墩塑性铰区抗剪强度试验［J］.中国公路学报，2011，24（2）：34－41.

［19］ 顾冬生，吴 刚，吴智深，等.钢筋混凝土圆柱考虑位移延性的受剪承载力研究［J］.土木工程学报，2010，43（S1）：118－123.

Comparison of Domestic and Overseas Code Regards to Shear Capacity of Reinforced Concrete Columns with Flexural－shear Failure

SHI Chengcheng，MA Ying，LUO Guojie，XU Xinyong
（School of Water Resources，North China University of Water Resources and Electric Power，Zhengzhou，He’nan 450045，China）

As a kind of failure mode under seismic load，flexural－shear failure’s process is very complicated and the research on the shear capacity of plastic hinge region is relatively inadequate.From the PEER（the Pacific Earthquake Engineering Research Center，USA）database for seismic performance testing of the columns，in accordance with the shear capacity of plastic hinge region，the quasi－static test data of 16 rectangular section columns failed in flexural－shear were collected.Through statistical analysis，the reliability of the shear capacity as provided in the standard of water conservancy industry in China，the Design Code for Hydraulic Concrete Structures（SL/T191-96）and the Design Code for Hydraulic Concrete Structures（SL191-2008）and in the standard of electric power industry in China，the Design Specification for Hydraulic Concrete Structures（DL/T5057-2009）was evaluated.The provisions of the shear capacity in the above codes were then compared to those in the main bridge seismic design specifications of the USA and Europe.The results show that these specifications can basically meet the requirements of shear capacity of columns with axial load ratio between 0.1～0.3.For the seismic design of the columns with axial load ratio less than 0.1 or more than 0.3，due attention should be paid.

reinforced concrete；column；seismic load；flexural-shear failure；shear capacity

TV332

A

1672—1144（2016）05—0020—06

10.3969/j.issn.1672-1144.2016.05.004

2016－06－20

2016－07－14

国家自然科学基金青年基金项目（51408223，51408222）；国家自然科学基金项目（U1404529）

石程程（1990—），女，黑龙江鹤岗人，硕士研究生，研究方向为工程结构抗震。E－mail：shicc1124@163.com

马 颖（1982—），女，河南郑州人，博士，硕士生导师，主要从事水工、桥梁与结构工程抗震研究。E－mail：maying198208@163.com