自升式平台踩脚印失稳机理大变形有限元分析

汪 纤，于 龙

（1.大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024；2.大连理工大学水利工程学院，辽宁大连116024）

自升式平台踩脚印失稳机理大变形有限元分析

汪 纤1，2，于 龙1，2

（1.大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024；2.大连理工大学水利工程学院，辽宁大连116024）

自升式平台桩靴踩脚印失稳相关研究较少，且多为实验研究，土体的流动破坏模式和桩靴失稳机制尚不十分清楚。运用CEL有限元方法来模拟桩靴贯入均匀土体的过程，选择出最合适的网格密度，在此基础上模拟桩靴在旧桩坑附近的二次插桩过程，分析了旧桩坑的几何形状（包括深度、坡度和直径）、二次插桩偏心距对桩靴基础二次插桩稳定性的影响规律，考察桩靴的最大峰值水平力Hmax、最大峰值弯矩Mmax，并联合土体的流动破坏机制分析了桩靴踩脚印失稳机理。

自升式平台；桩靴基础；旧桩坑；CEL方法

自升式钻井平台具有灵活性高、定位能力强、作业稳定性好，造价成本低等优点，在近海工程中有广泛的应用［1］。自升式平台作业包括拖航、沉桩、压载、升舱、拔桩等过程［2］。拔桩后常在海床上留下直径较大的孔洞，被称为“桩坑”或“脚印”。随着作业频次的增多，平台在相近甚至是同一位置进行二次或多次插桩作业的情况越来越多［3］。平台在桩坑附近再插桩，桩靴基础由于受到偏心或倾斜荷载作用而滑入桩坑，导致就位精度下降，并对桩腿及平台结构产生不利影响，严重时会导致桩腿弯曲变形，甚至平台与邻近导管架相撞，这种危险的状况称为踩“脚印”失稳，其破坏机制如图1所示［4］。

1 研究进展

Stewart D P等［5］采用离心机试验的方法研究了插桩偏心距的影响，结果表明，当插桩偏心距为0.5D至1.0D时水平推力明显增加，在0.75D时水平推力最大。Cassidy M J等［6］的离心机实验结果表明，插桩偏心距为0.5D时影响最大，超过1.5D时影响就非常小了。Gaudin C等［7］在离心机试验中将桩腿与作动器连接处铰接，结果表明脚印影响最大的偏心距为1.0D。Carrington T等［8］采用大变形数值计算的方法，仅分析了0.167D-0.407D范围内插桩偏心距的影响，得到水平力最大的偏心距为0.287D，该文结果同上述离心机试验结果差别较大。Gan C T［9］离心机试验结果表明，二次插桩桩靴直径相对尺寸越小，桩坑影响就越大。毛东风等［10］通过建立桩-土相互作用的流固耦合二维有限元模型，定性分析了桩坑对自升式钻井平台滑移风险的影响。赵军等［11］采用有限元方法分析了插桩偏心距对桩腿结构应力的影响。

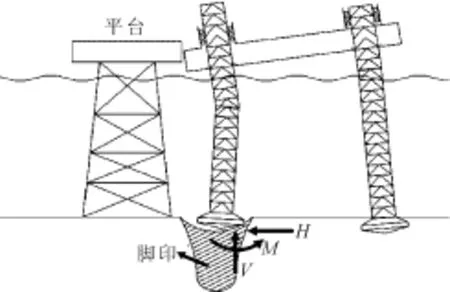
图1 平台在旧桩坑附近再插桩时的破坏机制

已有桩靴踩脚印稳定性研究多为离心机试验研究，仅能得到关键工况的桩靴受力，对土体的变形流动机理并不十分清楚。因此，本文采用耦合的欧拉-拉格朗日（CEL）有限元方法［12］建立桩靴-土体相互作用三维有限元模型，计算桩靴在旧桩坑附近就位贯入时受到的水平滑移力H，竖向力V和弯矩M，探讨旧桩坑的形状（深度和坡度）、插桩偏心距对二次插桩稳定性的影响，分析土体的变形破坏模式，为了解桩靴踩脚印失稳机理提供依据。

2 CEL有限元模型

2.1 模型的参数设置以及地基土体的本构模型

Sname［13］将桩靴基础简化等效为与其最大横截面面积相等的圆盘模型。Kong V等［14］在离心机实验中也采用这样简化的圆形桩靴基础，本文模拟的桩靴尺寸同文献［14］离心机试验工况一致，如图2所示，其弹性模量E=7.2×1010Pa，密度ρ=2 700 kg/m3，泊松比ν=0.3，桩靴直径D=15 m，对桩靴进行刚体约束。

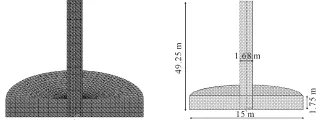
图2 桩靴数值模型

土体采用欧拉材料，在土体上方设置一定深度的空单元从而允许表面土体隆起。土体的应力应变关系用理想弹塑性模型来描述，且遵循摩尔-库伦强度准则。黏土的不排水抗剪强度su=7.5+0.92z（kPa），弹性模量E=500su（海洋黏土地基常用的刚

度指数［15］），有效重度，泊松比ν= 0.49，内摩擦角φ=0°，剪胀角ψ=0°。桩靴的加载贯入过程采用位移控制法来进行控制。综合考虑计算结果精度和计算机运行时间两个方面因素的影响，根据Qiu G等［16］的研究结果，选用v=0.5 m/s的贯入速度。

桩靴与土体的接触采用“通用接触”法则［17］。切向方向，假定桩靴表面为光滑；法线方向设为“硬接触”，接触面之间能够传递的接触压力大小不设上限，当接触压力变为0或负值时，接触分离。

2.2 网格优化

本部分采用纺锤形桩靴进行网格优化。

（1）桩靴网格划分技术的影响

采用ABAQUS提供的结构化、扫掠和自由三种技术对纺锤形桩靴进行网格剖分，得到的桩靴网格分别如图3所示，桩靴尖端部分均采用自由网格划分技术。

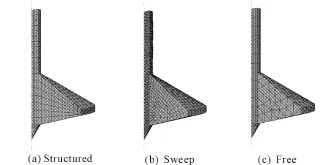
图3 桩靴不同的网格划分技术

计算得到的插桩阻力-桩靴贯入深度曲线如图4所示，各工况详细信息如表1所示。可以看出，桩靴网格采用不同的划分技术对插桩阻力影响不大，但是用Structured技术使大部分网格形状趋于规则，且计算耗时最少，因此本文之后的桩靴网格划分皆用如图3（a）所示的Structured网格。

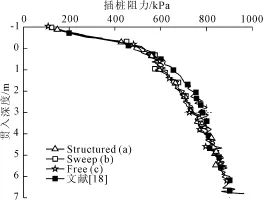
图4 桩靴网格划分形式不同对插桩阻力的影响

表1 桩靴网格优化

（2）土体网格密度的影响

不同网格密度的土体数值模型如图5所示，加密区最小网格宽度分别为bmin=0.5 m和0.25 m，桩靴外边缘单元尺寸保持hmin/D=1/24，桩靴直径为D=14 m。

图5 土体网格密度

计算结果如图6和表2所示。可以看出，bmin= 0.25工况的插桩阻力比bmin=0.5 m工况减少了5%左右，但是计算时间提高了4倍多。总体上看，本文计算结果同Craig&Chua［18］的离心机试验结果吻合较好。综合考虑计算精度和效率，本文后续计均采用bmin=0.5 m方案。

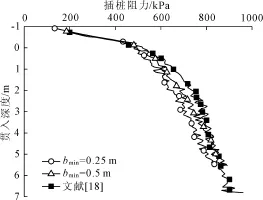
图6 土体网格密度不同对插桩阻力的影响

表2 土体网格优化

（3）桩坑网格优化

采用人工挖取的方法形成倒圆锥形桩坑，圆锥形表面为弧面，给生成格式化网格带来了困难。为解决这一问题，首先建立一个无参数、不施加任何边界条件的拉格朗日参考几何体，如图7（a）所示，然后用体积分数工具（Volumn Fraction Tool）自动计算出欧拉单元中土体材料所占的欧拉体积分数，最后在可视化（Visualization）模块中可以看到有桩坑的单元网格形状，如图7（b）所示。

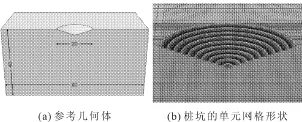
图7 桩坑单元网格划分

最终，地基整体模型为长方体，地基模型宽度为8D，深度为4D，厚度为8D。取1/2对称模型，底部约束三个平移自由度。四周约束法向平移自由度。桩靴网格划分采用线性减缩积分单元，土体网格划分采用唯一的欧拉单元EC3D8R，最小网格尺寸为0.5 m。

3 计算结果与讨论

3.1 计算工况

Kong V等［14］在鼓式离心机中用切割刀片人工切出的三种理想倒圆锥形桩坑TA、TB、TC，其斜坡角度分别为9.5°、18.4°、33.7°，桩坑的深度在0.17D～0.67D，这种人造的理想桩坑可以使其周围土体的扰动程度降到最低，能够消除土体的不均匀性带来的影响。TA、TB、TC桩坑数值模型平面图如图8所示，TA-2D中TA代表桩坑种类，2D代表桩坑的直径，以此类推。桩靴在旧桩坑附近插桩时采用的关键参数符号如图9所示。数值模拟了24种工况列于表3。

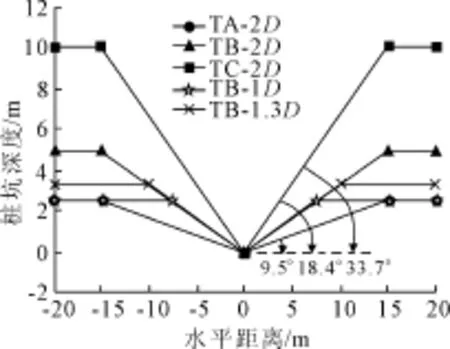
图8 桩坑模型简略图

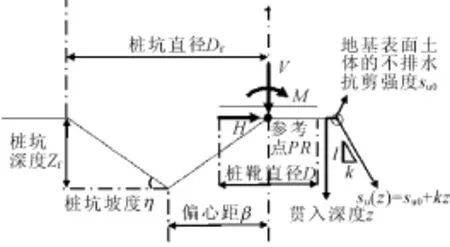
图9 参数符号及意义

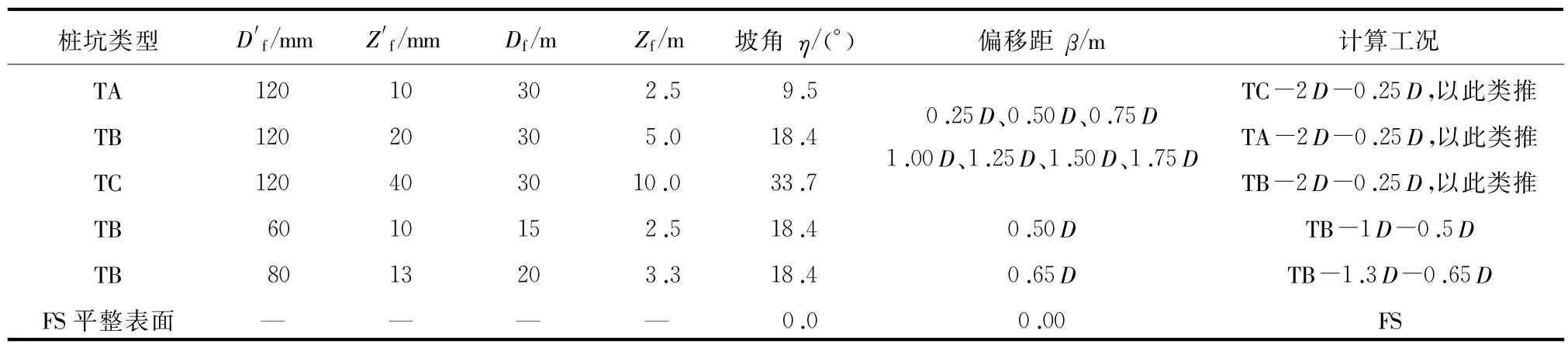
表3 数值模拟工况

3.2 计算结果与讨论

3.2.1 偏心距β的影响

距离桩坑TB不同偏移距处插桩时桩靴受到的竖向反力V、水平滑移力H、弯矩M与Kong V等［14］的实验工况（桩坑TB，其直径为2D，偏心距为1.0D）对比如图10所示，土体流动机制如图11所示。本文计算无量纲化竖向反力V/suA的极限值在13和14之间，同刘君等［19］的大变形数值计算结果吻合较好。相比之下Kong V的离心机试验结果仅有V/suA=9.0左右，明显偏小，这可能是由于试验过程中土体存在一定强度软化特性。由图10的工况TB-2D-1.0D的荷载对比分析可以看出桩坑对插桩反力的影响：（1）桩靴刚贯入地基深度z/D=0.04时，弯矩M马上就达到了峰值Mmax，此时水平力很小；（2）当桩靴贯入深度达到桩坑底部位置（z/D=0.33）时，水平力H达到了峰值Hmax；（3）当桩靴贯入深度达到z/D=0.6时，峰值荷载Mmax、Hmax减小到几乎为0，此后随着贯入深度的增加桩坑对插桩反力几乎没有影响了。下面结合流动机制分析V、H、M的产生和发展机理。

对偏心距为1.0D工况，当桩靴在预压载作用下贯入深度z/D=0.04时，桩靴与土体部分接触，桩靴下面的土体分别向左右出现两种滑弧形破坏机制，见图11（c）所示。由于桩坑的存在，土体明显向桩坑侧滑动，整体滑裂面发展的深度低于FS工况（见图11（a））。这就是贯入深度较浅时有桩坑工况竖向插桩阻力比无桩坑工况小的原因。有桩坑情况下，贯入深度较浅时桩靴左侧悬空，导致弯矩急剧增加达到峰值。由于桩靴贯入深度较浅且桩靴表面光滑，此时水平反力并未发展。

z/D=0.33时，虽然能看到两种流动机制，但其不对称性减小，竖向阻力V与桩靴在平整地基插桩时的几乎相等，弯矩减小。桩靴右侧土体开始回流并对桩靴产生水平推力，而左侧土体并未回流，因此此时总水平力达到峰值。

z/D=0.6时，流动机制的左右不对称性进一步减小，桩坑大部分被填平，有桩坑工况竖向反力几乎同无桩坑工况一致，弯矩减小到几乎为0。桩靴两侧的土体都能看到回流，水平反力减小。

对偏心距为0.5D工况，如图11（b）所示，桩靴与地基刚接触（z/D=0.04）时，桩靴右端接触桩坑右肩左端悬空，因此产生一定水平推力和弯矩。但此时桩靴同土体接触面积较小，水平力和弯矩的数值都不大。随着贯入深度的增加，弯矩有所发展，弯矩最大值发生在z/D=0.12处。桩靴左端在z/D =0.12附近接触地基，从而产生向右侧的水平力，从此处开始桩靴整体水平力减小。随着贯入深度的进一步增加，桩靴右端土体首先开始回流，此时水平力又开始增加；随后桩靴左侧土体也开始回流，水平力再次减小。三种偏心距工况的水平力最大值都发生在z/D=0.33附近。

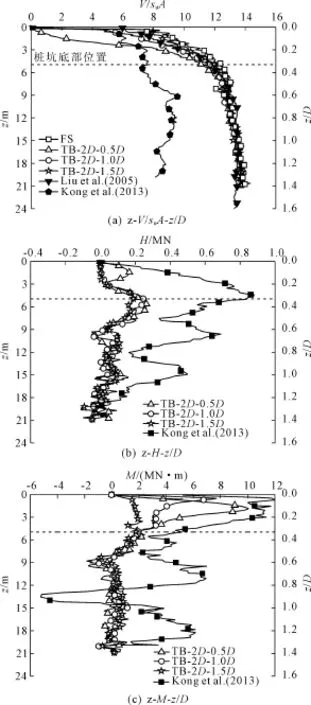
图10 桩坑在桩坑TB附近插桩时的载荷

对偏心距为1.5D工况，如图11（d）所示，初始贯入时桩靴底部左右均与土接触，因此所受弯矩较小。弯矩最大值发生在z/D=0.2附近，其数值仅为偏心距0.5D和1.0D工况的1/3～1/2。

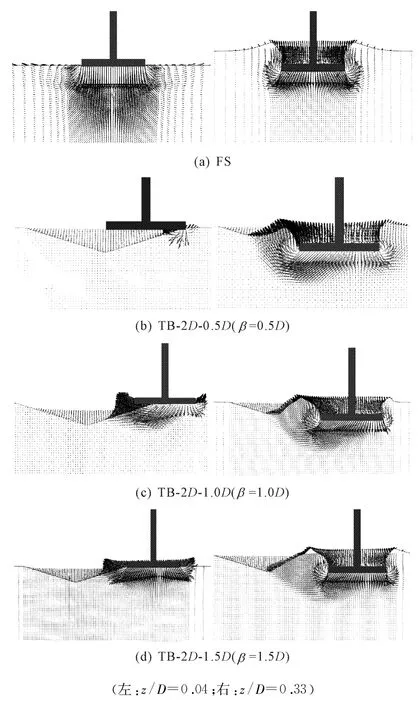
图11 桩靴在桩坑TB附近不同偏心距插桩时的流动机制

图12总结了桩靴在桩坑附近不同偏心距插桩时的峰值荷载Hmax、Mmax值，当β=0.5D峰值荷载达到最大值，β=0.5D被称为临界偏心距。Cassidy M J等［6］以及Gan C T等［9］都发表过临界偏心距在0.5D～1.0D之间。3.2.2 桩坑大小的影响

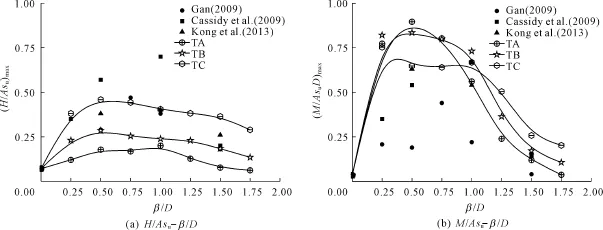
图12 不同偏移距下的峰值荷载与实验数据的对比

改变桩坑TB的形状，考察三组不同深度为2.5 m，3.3 m，5.0 m的TB桩坑，其坡角η都是18.4°，对应的桩坑直径分别为1D，1.3D，2D，且偏心距与桩坑直径的比值都等于1/2，即桩靴中心线都位于桩坑的边缘上。这样就可以在β/Df值不变的情况下考查桩靴在不同桩坑深度下插桩时受到的竖向反力V、水平力H、弯矩M如图13所示，土体的流动机制如图14所示。

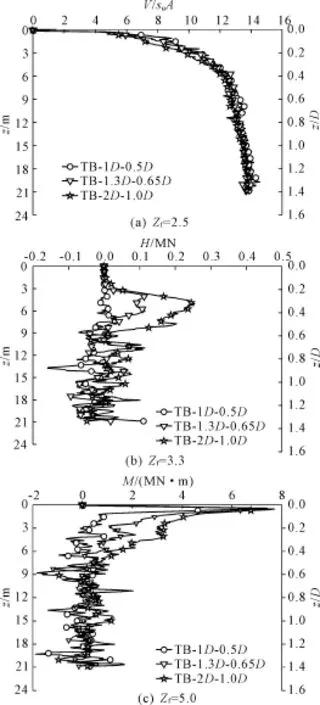
图13 桩靴在深度不同的桩坑TB附近插桩时的载荷

当z/D=0.04时，三个工况弯矩达到最大值，且Mmax数值相差不大。这是因为此时这三个工况的桩靴都是右半部分与土接触而左半部分悬空，土体的承载机制相同。随着贯入深度的增加，尺寸较大的桩坑影响也较大，导致弯矩减小幅度比较缓慢。

对于水平力，桩坑越大，水平力也越大。较小桩坑（Zf=2.5 m）的水平力很小。Zf=3.3 m和5.0 m两个工况的最大水平力均发生在z/D=0.33附近。

表4总结了桩靴在不同深度桩坑附近插桩时的峰值荷载Hmax、Mmax值。桩坑的大小对水平力具有重要影响，而对弯矩影响很小。这一结论与文献［14］的试验结果相符。

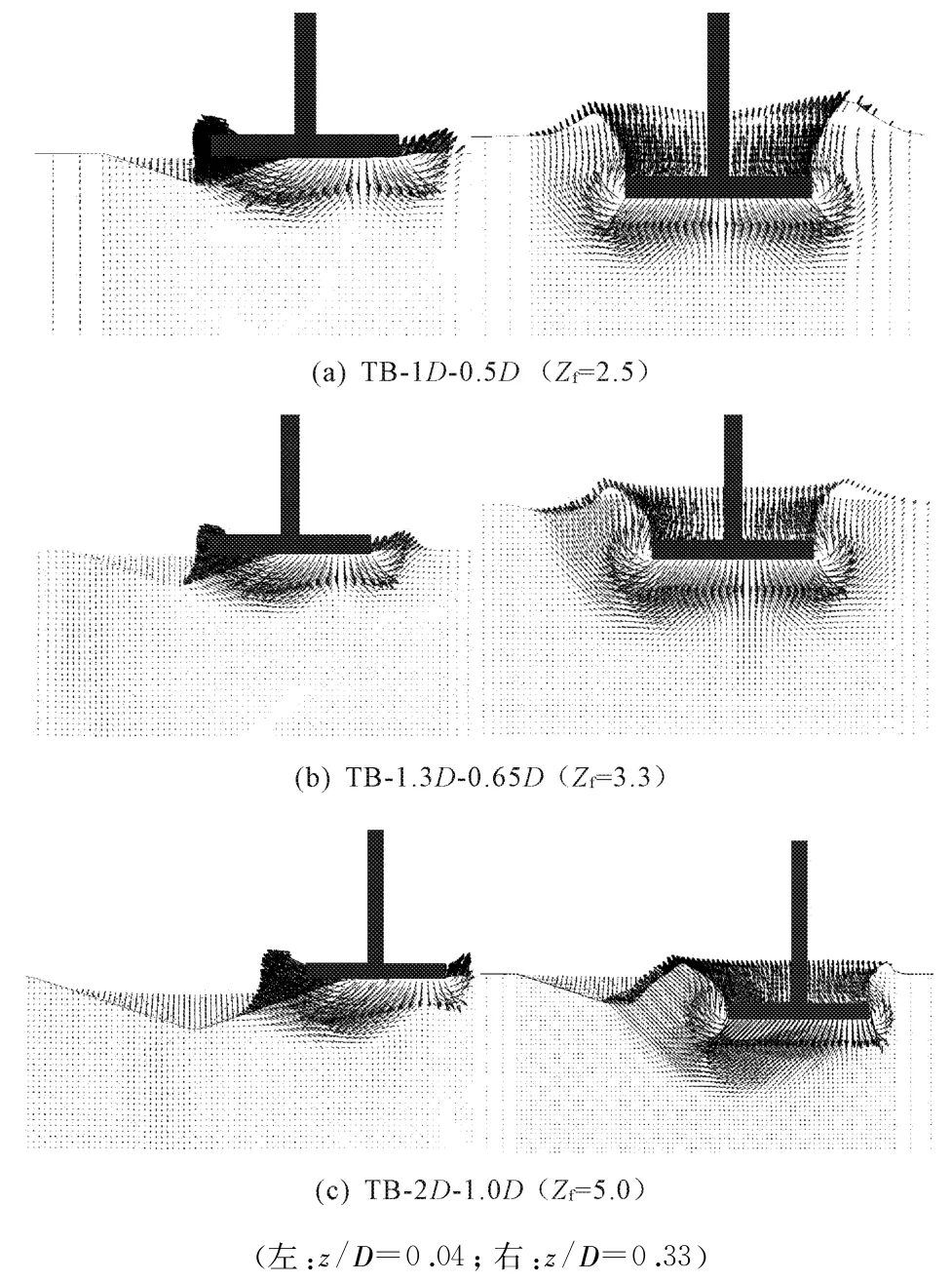
图14 桩靴在形状不同的桩坑TB附近插桩时流动机制

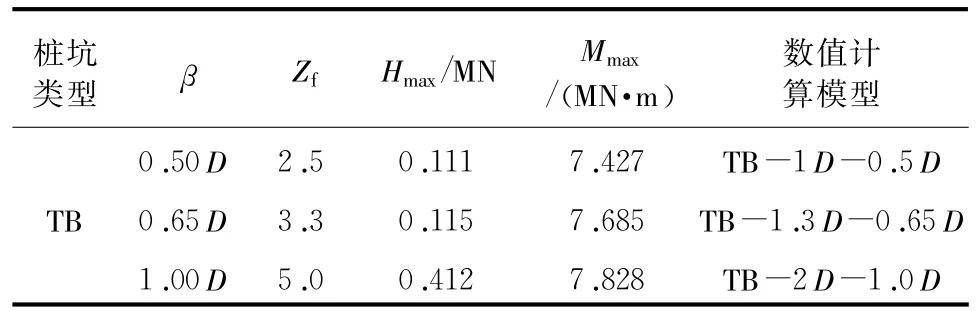
表4 桩靴在不同深度的TB桩坑附近插桩时的峰值荷载

3.2.3 桩坑坡度η的影响

考虑直径相同，深度与坡度都不相同的三种桩坑TA、TB、TC，桩靴在三种桩坑附近（β=1.0D）插桩时受到的竖向反力V、水平力H、弯矩M对比如图15所示。

三个工况的最大弯矩均发生在桩靴刚开始接触土体时。坡度较大的桩坑，峰值弯矩数值也比较大。同上节类似，随着贯入深度的增加，坡度较大（或者说深度较大）的桩坑影响也较大，导致弯矩减小幅度比较缓慢。

桩坑坡度（深度）对水平力影响较大。桩坑越深，桩靴左侧土体出现回流机制越晚，桩靴的水平推力也就越大。桩靴在TC附近插桩时的峰值水平力是在TA附近插桩时的3倍左右。

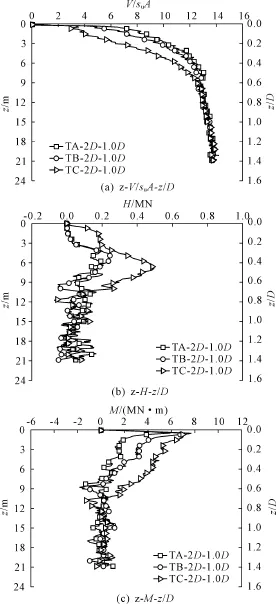
图15 桩靴在TA、TB、TC桩坑附近（β=1.0D）处插桩时的荷载

4 结 论

通过运用CEL大变形有限元方法模拟平底桩靴踩脚印插桩过程，了解到平底桩靴受到弯矩作用的最不利位置为桩靴一半在坡肩、一半在桩坑上方悬空的位置。最大弯矩发生的位置在桩靴刚与土体接触阶段。桩坑大小和深度对桩靴所受弯矩的影响较小，对水平力的影响较大。综合水平力和弯矩计算结果，平底桩靴插桩的最不利偏心距为β=0.5D。

［1］ 张鹏飞，于兴军，栾 苏，等.自升式钻井平台的技术现状和发展趋势［J］.石油机械，2015，43（3）：55－59.

［2］ 杜家庆，杜守继，赵丹蕾，等.自升式钻井平台桩靴基础结构设计分析［J］.水利与建筑工程学报，2012，10（6）：96－101.

［3］ 毛东风，张明辉，张来斌，等.遗留桩坑对自升式平台滑移风险的影响及对策［J］.石油勘探与开发，2015，42（2）：233－237.

［4］ Kong V W.Jack－Up Reinstallation near Existing Footprints［D］.Perth，Australia：University of Western Australia，2012.

［5］ Stewart D P，Finnie I.Spudcan－footprint interaction during jack－up workovers［J］.Evolutionary Ecology Research，2001，3（1）：107－116.

［6］ Cassidy M J，Quah C K，Foo K S.Experimental investigation of the reinstallation of spudcan footings close to existing footprints［J］.Journal of Geotechnical and Geoenvironmental Engineering，2009，135（4）：474－486.

［7］ Gaudin C，Cassidy M J，Donovan T，et al.Spudcan reinstallation near existing footprints［C］//Proceedings of the 6thInternational Conference of Offshore Site Investigation and Geotechnics.Confronting New Challenges and Sharing Knowledge.London：Society of Underwater Technology，2007.

［8］ Carrington T，Hodges B，Aldridge T，et al.Jack－up advanced foundation analysis by automatic remeshing large strain FEA methods［C］//［s.l］：［s.n］，1981：23－24.

［9］ Gan C T.Centrifuge model study on spudcan－footprint interaction［J］.National University of Singapore，Singapore，2009.

［10］ Bolton M D，Osman A S.Simple plasticity－based prediction of the undrained settlement of shallow circular foundations on clay［J］.Géotechnique，2005，55（6）：355－356.

［11］ 赵 军，段梦兰，宋林松，等.自升式钻井平台就位时老脚印对桩靴性能的影响分析［J］.中国海上油气，2014，26（5）：104－108.

［12］ 郑 静，范庆来，王忠涛.纺锤形桩靴基础贯入过程Eulerian－Lagrangian耦合有限元法的模拟［J］.工业建筑，2013，43（12）：104－108，161.

［13］ Sname.Recommended practice for site specific assessment of mobile jack－up units［C］//Technical and Research Bulletin 5－5A，First ed，Rev 3：Jersey City，NJ：Society of Naval Architects and Marine Engineers，2008.

［14］ Kong V，Cassidy M J，Gaudin C.Experimental study of effect of geometry on reinstallation of jack－up next to footprint［J］.Canadian Geotechnical Journal，2013，50（5）：557－573.

［15］ 周 琪，于 龙.考虑黏土应变软化的锚板承载力数值分析［J］.水利与建筑工程学报，2014，12（4）：124－128.

［16］ Qiu G，Henke S.Controlled installation of spudcan foundations on loose sand overlying weak clay［J］.Marine Structures，2011，24（4）：528－550.

［17］ 王 鹏，王建华.钻井船插桩的大变形有限元数值模拟［J］.低温建筑技术，2013，35（2）：100－101.

［18］ Craig W H，Chua K.Deep penetration of spudcan foundations on sand and clay［J］.Géotechnique，1990，40（4）：541－556.

［19］ Liu J，Hu Y X，Kong X J.Deep penetration of spudcan foundation into double layered soils［J］.China Ocean Engineering，2005，19（2）：309－324.

Large Deformation Finite Element Analysis of the Failure Mechanism of Jack－up’s Reinstallation near Footprints

WANG Qian1，2，YU Long1，2
（1.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China；2.School of Hydraulic Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

Most of the existing researches on the interaction between spudcans and footprints are obtained by model tests. The failure mechanisms during reinstallation are still not very clear.This study firstly carried out Coupled Eulerian-Language（CEL）analyses to simulate processes of spudcan installed in homogeneous soils.The most suitable mesh density was selected.After that reinstallation processes of spudcans close to existing footprints were simulated.Effects of footprint geometry（depth，slope angle and diameter）and reinstallation offset on the developing behaviors of vertical resistance，horizontal resistance and moment acting on spudcan.The soil flow mechanisms during a spudcan reinstallation near an existing footprint were discussed.

jack－up unit；spudcan；footprint；coupled Eulerian-Lagrange method；

TU44

A

1672—1144（2016）05—0030—07

10.3969/j.issn.1672-1144.2016.05.006

2016－04－23

2016－06－04

国家自然科学基金项目（51539008，51479027）；中央高校基本科研业务费专项基金（DUT15LK36）

汪 纤（1991—），女，安徽安庆人，硕士研究生，研究方向为土与结构的相互作用。E－mail：1030571277@qq.com