小尺寸双柱式桥墩波浪力的数值分析
柳春光,李璐璐,张士博
(1.大连理工大学建设工程学部,辽宁大连116024;
2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024)
小尺寸双柱式桥墩波浪力的数值分析
柳春光1,2,李璐璐1,张士博1
(1.大连理工大学建设工程学部,辽宁大连116024;
2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024)
Morison方程适用于小直径孤立柱的波浪力计算,对于双柱式桥墩的波浪力计算已不能直接采用Morison方程。为了能利用Morison方程求解双柱式桥墩的波浪力,定义了双柱式桥墩前柱、后柱及整体结构的波浪力干扰系数。采用线性波浪理论,利用推板式造波方法模拟线性波,将ANSYS Workbench平台作为FLUENT和ANSYS的数据传递平台,对深水环境下双柱式桥墩受到的波浪力以及波浪场作用下双柱式桥墩的结构变形进行单向流固耦合数值模拟。数值模拟结果表明,双柱式桥墩前、后柱波浪力的干扰系数在一定柱距范围内均随柱距的增大近似的成线性增大,当柱距超过一定值后趋于稳定。由于双柱间存在相位差,双柱墩波浪力的总干扰系数以及双柱墩的结构变形却随着双柱中心距的增大而减小。这些变化曲线为实际工程中深水桥梁双柱式桥墩的波浪荷载计算提供了一种更为简便的算法。
Morison方程;线性波;双柱式桥墩;流固耦合;结构变形
深水桥梁主要分为三种[1]:第一种是建在江、河上的桥梁;第二种是建在水库中的桥梁;第三种就是现在发展迅速的跨海大桥。对于这些深水桥梁,受到的荷载情况比较复杂,例如波浪与水流作用、地震作用以及风载都是主要的动荷载[2],这些动荷载主要作用在深水桥梁的基础部分。其中,波浪荷载作为一种永久的主要动荷载,在深水桥梁工程设计中引起了人们极大的注意。
对于单柱结构的波浪荷载计算目前仍广泛采用Morison方程,但对于双柱或多柱式结构的波浪力求解则相当复杂。Bushnell M J[3]在振荡水洞中研究了两个桩和3×3组合桩之间的相互干扰;Sarpkaya T等[4]用振荡水流对不同桩柱的两个桩进行了实验;Chakrabarti S K[5]在波浪水槽中测量了并列2个桩、3个桩和5个桩在不同桩距时的波浪力;王爱群等[6]、徐立论等[7]试验研究了单排两桩、三桩、2×2组合桩3×3组合桩、4×4组合桩的波浪力;俞聿修等[8-9]试验研究了不规则波作用下双桩上的波浪力。本文通过对双柱式桥墩进行波浪作用下的数值模拟[10]可以建立简便、有效的双柱式结构波浪力求解公式,为实际桥梁工程设计提供一定的依据。
本文以ANSYS Workbench平台作为计算流体力学软件FLUENT和有限元结构分析软件ANSYS的数据传递平台[1],对不同柱距的圆形截面双柱式桥墩结构在波浪场中进行单项流固耦合数值模拟[11],得到了双柱式桥墩的前柱和后柱以及整个双柱式结构在波浪场中受到的波浪力干扰系数的变化规律。
1 理论分析
1.1 波浪理论
在海洋工程中,波浪理论分为线性波浪理论和非线性波浪理论。对于线性波浪理论我们通常采用微幅波理论;非线性波浪理论主要包括Stokes波理论、孤立波理论、椭圆余弦波理论等,本文主要介绍微幅波理论。
微幅波理论又称Airy波理论,是用势函数来研究波浪的运动。微幅波理论忽略了函数中非线性项的影响,由此可以将问题线性化,得到线性波的势函数[12]:
波面方程:
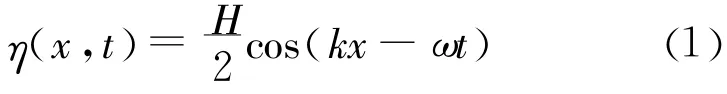
速度势函数:
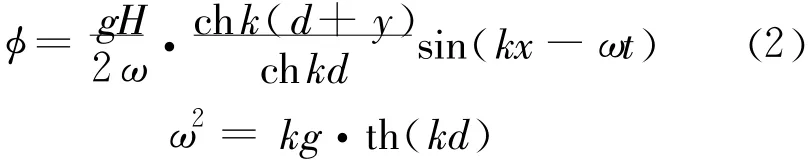
根据速度势可以求得波浪水质点的水平速度、垂直速度、水平加速度和垂直加速度。
水平速度:
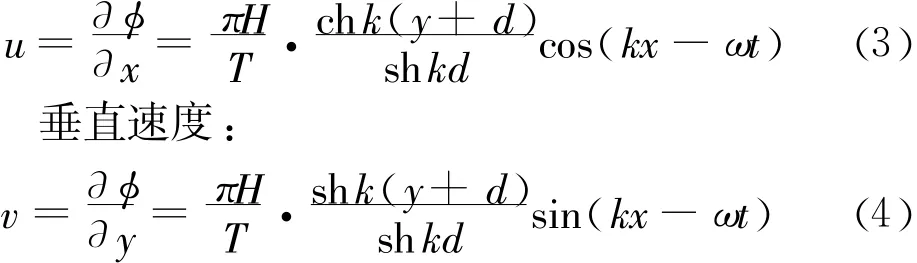
水平加速度:
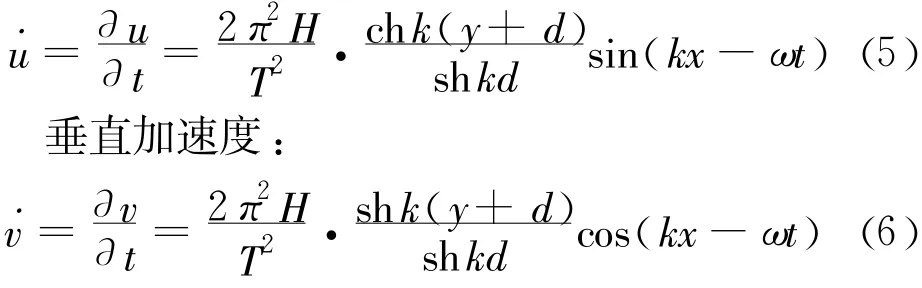
式中:H为波高;L为波长;T为周期;ω为频率;d为水深;k为波数,
1.2 推板式造波
本文中波浪的生成采用推板式造波方法[13-14],推板式造波是一种仿物理造波,即用数值方法模拟实验室物理造波机进行造波。推板式造波的原理是将水池的波浪入口边界作为动边界,通过模拟动边界做简谐运动,使水池中的水产生波动,进而形成波浪。推波板做简谐运动的速度[13]为:
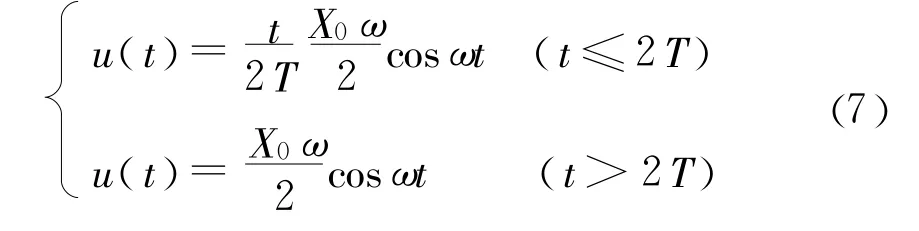
式中X0是推波板的冲程,其中在t≤2T时间内,由于刚开始造波,所以对推波板的速度进行了关于时间的光滑处理。
已知推波板的速度方程,运用微幅波理论,并且在结果中忽略掉了只产生局部干扰的非传播项,最后得到了推板式造波的波面方程以及速度势函数[14]如下:

在用FLUENT模拟波浪场时,没有现成的波浪模型可以直接运用,需要用户编写C程序自定义波浪模型,在推板式造波的程序中,我们需要先根据式(1)和式(8)求出推波板的冲程X0。
1.3 Morison方程
在工程设计中,计算桩柱上的波浪力的方法[10]主要有两种,一种是1950年由Morison等人提出的Morison方程,这种方法主要适用于桩柱直径D与波长L之比较小,即D/L≤0.15时;另一种是1954年由Mac Camy和Fuchs提出的绕射理论,在D/L>0.15情况下,一般会考虑运用绕射理论进行波浪力计算。
本文中的D/L=2/25=0.08<0.15,波浪力的计算可以采用Morison方程。Morison方程包含了两部分力,一部分称为速度力fD,另一部分称为惯性力fI,即单位高度桩柱上的总水平波浪力为:
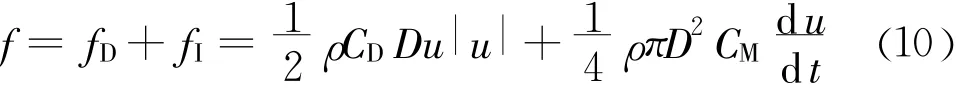
式中:CD、CM分别为阻力系数和惯性力系数;ρ为水的密度;u为水质点水平速度为水平加速度,可分别根据式(3)和式(5)求得。将式(10)从水底y =-d到波面η(x,t)积分可得到整个桩柱上的水平波浪力[15]:

式中:

2 流固耦合
流固耦合问题[16]主要研究流体和结构之间的交互作用,即结构在运动流体的荷载作用下会产生运动或变形,而结构的运动或变形反过来又会影响到运动流体的荷载分布及大小,是一门交叉性学科。数值模拟中的流固耦合问题有单向流固耦合和双向流固耦合。单向流固耦合是指流固交界面处的数据传递是单向的,即只考虑流体荷载对结构的影响;双向流固耦合是指流固交界面处的数据传递是双向的,不仅考虑流体荷载对结构的影响,还考虑结构的变形或运动对流体荷载产生的影响。本文中结构物的D/L=0.08,属于小尺寸结构物,它的变形对流场的影响很小;其次考虑到双向流固耦合对计算机配置的要求相对较高、计算时间较长;所以本文采用单向流固耦合进行分析。
本文在ANSYS Workbench平台上实现了FLUENT和ANSYS之间的数据传递。首先利用FLUENT计算得到流场中耦合边界上的压强,ANSYS Workbench平台将计算得到的压强以耦合边界节点插值的方式传递给ANSYS,在外荷载的作用下,ANSYS计算得到结构物的位移。此过程便完成了单向流固耦合的数值模拟。
3 流固耦合数理模型
3.1 物理模型
本文建立的深水环境下的双柱式桥墩的模型如图1所示。
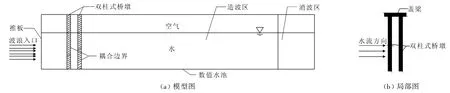
图1 双柱式桥墩简图
在该数值模拟中,双柱式桥墩的墩柱直径D=2 m,墩柱高l=30 m,前柱放置在X=15 m处,双柱之间的距离与直径之比S/D分别取1.5、2.0、3.0、4.0、5.0五种不同的工况。波浪要素分别为:波长L =25 m,波高H=1 m,周期T=4 s,水深d=20 m。由于D/L=2/25=0.08≤0.15,属于小尺寸墩柱结构,可以用Morison方程来验证数值模拟的孤立桩的波浪力的大小。
3.2 流场计算模型
本文中的波浪形式采用的线性微幅波。利用推板冲程X0、波长L、周期T等参数编写C程序在FLUENT中UDF二次开发来模拟推板式造波,并在流域尾端采用多孔介质消波法[13]进行消波。
由于波浪水质点的运动速度只有在自由水面附近是显著的,所以在对流场划分网格时,对气液两相交界面上下一个波高范围内进行网格加密处理;为了能更准确的监测柱面周围的波浪力,对柱周围也进行加密处理,加密过后的流场总单元数为864 432,结点数为903 011。整个流场域、双柱周围以及水面处的网格划分示意图如图2所示。
3.2.1 边界条件
流体域为气液两相流模型。
(1)定义水池左右两侧边界、前后两侧边界以及水池底部均为壁面边界条件Wall,其中左侧的推板边界设置为动边界。
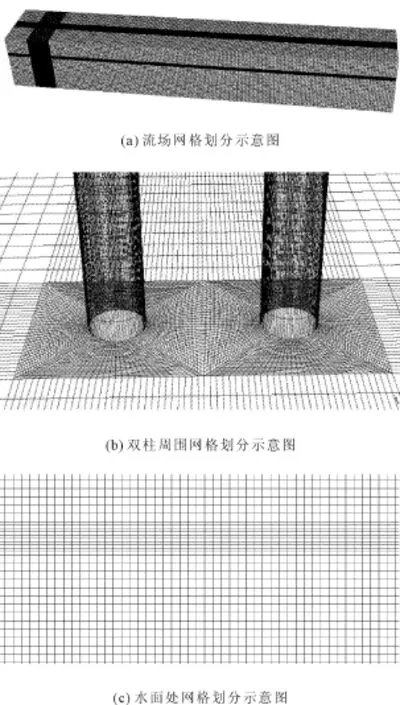
图2 网格划分示意图
(2)定义水池自由上表面为压力入口边界条件Pressure-inlet,指定压力为一个大气压。
(3)定义双柱结构外表面为耦合边界。
3.2.2 数值计算方法
流场计算采用FLUENT软件,以连续性方程和不可压缩黏性N-S方程作为流体运动控制方程,采用VOF模型,UDF二次开发功能,Segregated求解器,标准k-ε模型,PISO算法对流体域进行求解运算。
3.3 结构计算模型
本文的结构场为整个双柱式桥墩,定义结构的密度为2 500 kg/m3,泊松比为0.2,弹性模量为3.0×1010Pa,双柱底端固结,顶端以盖梁结构约束。在数值模拟中,有限元模型采用Solid 186单元,采用自定义网格划分方法将模型全部划分为六面体网格,网格总单元数为191 791,节点数为208 837,网格划分示意图如图3所示。定义双柱的外表面为耦合面,与流体模型中的耦合边界相吻合。在耦合过程中,先求解FLUENT,待每个时间步长计算结束后利用Workbench平台将耦合边界的数据传递给ANSYS进行结构计算。
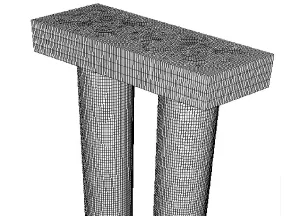
图3 双柱式桥墩的网格划分示意图
4 计算结果及分析
4.1 Morison方程求解单柱波浪力
本文中的柱径为D=2 m,前文中已验证该柱属于小尺寸桩柱,可以用Morison方程来求解波浪荷载,依据海港水文规范[17],取CD=1.2、CD=2.0。已知波长L=25 m,波高H=1 m,周期T=4 s,水深d=20 m,代入到式(1)、式(11)、式(12)、式(13)中即可得到整个桩柱上的水平波浪力。由于波面方程不是一个定值,而是随时间变化的函数,所以由水底到波面积分得到的是一个随时间变化的函数,取函数的最大值即为最大水平波浪力Fmax=31.029 kN。
4.2 数值模拟单柱波浪力
对波浪数值水池进行验证[15]时,得到X=15 m的数值波高和X=15 m、水深为1 m处的数值水平速度都与理论值相吻合,验证了本文数值波浪模拟的正确性,数值模拟的波高曲线和数值模拟的水平速度曲线与理论值的对比如图4(a)、图4(b)所示。
在用FLUENT对单柱进行数值模拟时,将单柱放置在水池X=15 m处,流场计算过程中FLUENT监测到的是无量纲的拖拽力系数Cd的大小,为了得到水平波浪力Fd,需要进行转化,转化公式如下:
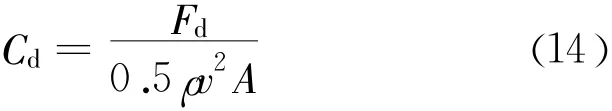
式中:ρ、v、A分别为水的密度、参考速度和面积,这三项都是在FLUENT中的Reference Values对话框中进行自定义设置。
经过转化后的数值波浪Fdmax=29.359 kN,与Fmax=31.029 kN的误差仅为5%,在容许误差范围内,这说明本文中用数值模拟方法计算波浪力是可靠的,数值波浪力与理论波浪力的对比如图4(c)所示。
图4(a)中波峰处的波幅比理论波幅要大一点[14],这是由于推波板的干扰造成的,离推波板越远,这种现象会逐渐消失;图4(b)、图4(c)中波谷处的水质点水平速度和波浪力小于波峰处,这主要是因为数值模拟过程中考虑了水平面以下流体的黏性作用,而求解理论值时认为液体是无黏性的。
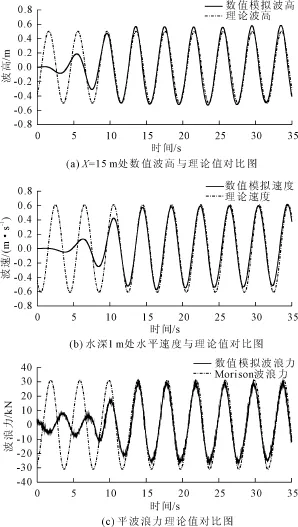
图4 数值模拟值与理论值对比图
4.3 数值模拟双柱式桥墩
对于双柱式桥墩受到的波浪力,由于柱间存在相位差以及双柱之间的互相干涉,已不能直接用Morison方程进行求解,为了能直接利用Morison方程求双柱式桥墩的波浪力,本文定义了干扰系数[6]。
本文主要研究双柱式桥墩的各柱受到的波浪力的无量纲干扰系数随柱距的变化而产生的变化。定义双柱式桥墩中前柱的干扰系数[8]为:

后柱的干扰系数为:

双柱式桥墩整体干扰系数为:

其中:FG1、FG2是双柱式桥墩中前柱和后柱受到的波浪力的峰值;FG是双柱式桥墩受到的波浪力峰值;F0是孤立柱受到的波浪力的峰值。
(1)本文中分别将柱中心距与柱径之比S/D设为1.5、2.0、3.0、4.0、5.0,不同柱距时各柱以及整个双柱式结构受到的正向波浪力的峰值如表1所示。
根据式(15)、式(16)、式(17)可分别求得前柱干扰系数,后柱干扰系数,整体干扰系数,并绘制曲线图如图5(a)~图5(c)所示。
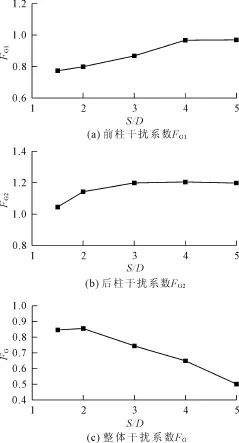
图5 干扰系数曲线图
由表1可以看出,由于柱间存在相位差以及双柱之间的相互干扰,使得5种工况下的双柱式桥墩的整体波浪力峰值都小于前柱和后柱波浪力峰值之和。
图5(a)是前柱在不同柱距时干扰系数的变化趋势。由于后柱对前柱的抑制效应,使得前后柱中间的流体压力升高,减小了前柱的前后压差,导致其所受到的波浪力减小。从图5中可以看出前柱的干扰系数随着柱距的增大而增大,在S/D时趋于稳定,稳定的干扰系数值接近于1。
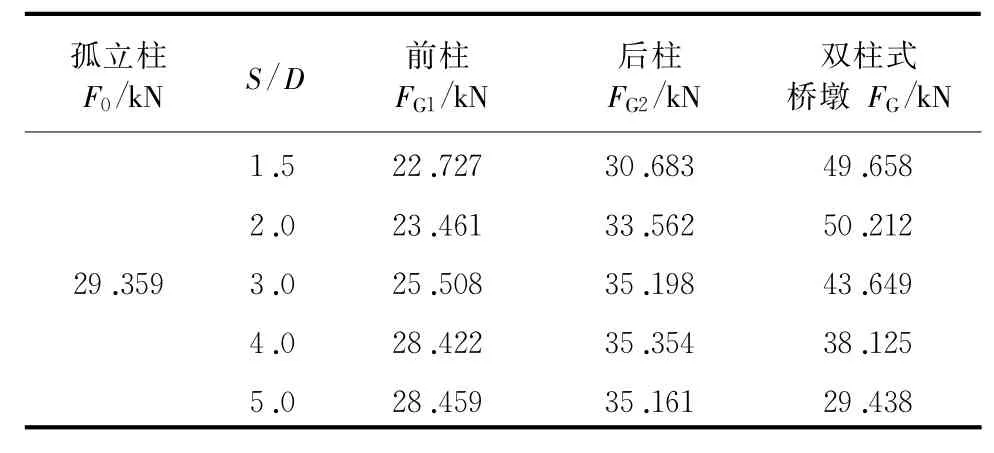
表1 各柱正向波浪力峰值
图5(b)是后柱在不同柱距时干扰系数的变化趋势。由于前柱对后柱有遮蔽效应导致后柱的干扰系数随着柱距的增大而增大,在S/D=4时趋于稳定,稳定的干扰系数值接近于1.2。由于抑制效应起主要影响作用,在相同柱距时,后柱干扰系数大于前柱干扰系数。
图5(c)是整个双柱式桥墩在不同柱距时干扰系数的变化趋势。由于相位差的存在,使得整体的干扰系数随着柱距的增大而减小。
在工程设计中,我们可以先利用Morison方程求得单柱的波浪力,再根据本文中图5(a)~图5(c)所示的曲线,采用式(18)简单快速的计算出双柱式桥墩上的波浪力。
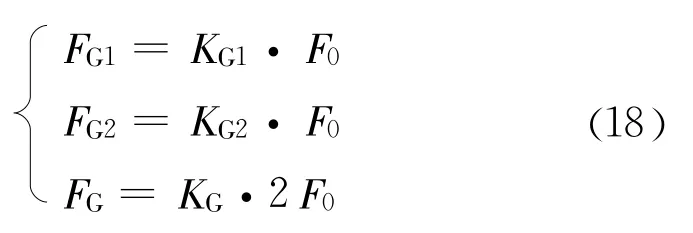
(2)Bushnell M J[3]、Sarpkaya T[4]、王爱群等[6]、俞聿修等[8-9]都试验研究了串列小直径组合桩的波浪力与KC数[19]和桩距之间的关系,得出了相似的结论。通常定义,对于规则波,u是静水
m面处水质点的最大水平速度,T为周期,D为柱径。
其中王爱群试验得出,在规则波作用下前桩和后桩的干扰系数均随着桩距的增大而增大,由于抑制效应,后桩干扰系数会大于前桩,并且在小KC数时,后桩的干扰系数大于1;俞聿修试验结果表明,在不规则波浪作用下,前桩和后桩的群桩系数都会随着桩距的增大增大,由于后桩的存在,改变了前桩的尾流情况,使得前桩波浪力出现小于后桩的现象,并且后桩的群桩系数在一些情况下大于1。
本文采用的是线性波,波浪参数是恒定的,根据KC数的定义,可求得本文中的KC数是个定值,所以本文只考虑了柱距对干扰系数的影响。本文数值模拟的干扰系数与王爱群等人试验的干扰系数对比如图6所示,对比结果表明在定KC数情况下,本文用数值模拟方法得出的结果与上述两个试验结果大体一致。
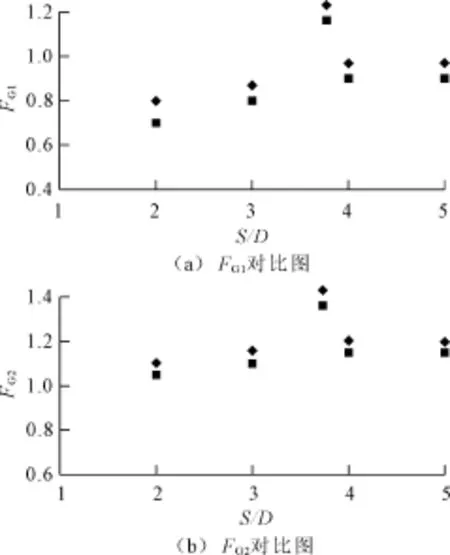
图6 与王爱群文献对比图
4.4 结构响应
对于单柱以及双柱结构在波浪力作用下的柱顶最大响应如表2所示;X=15 m处的孤立柱和S/D =3时的双柱式桥墩的柱顶位移曲线如图7所示。
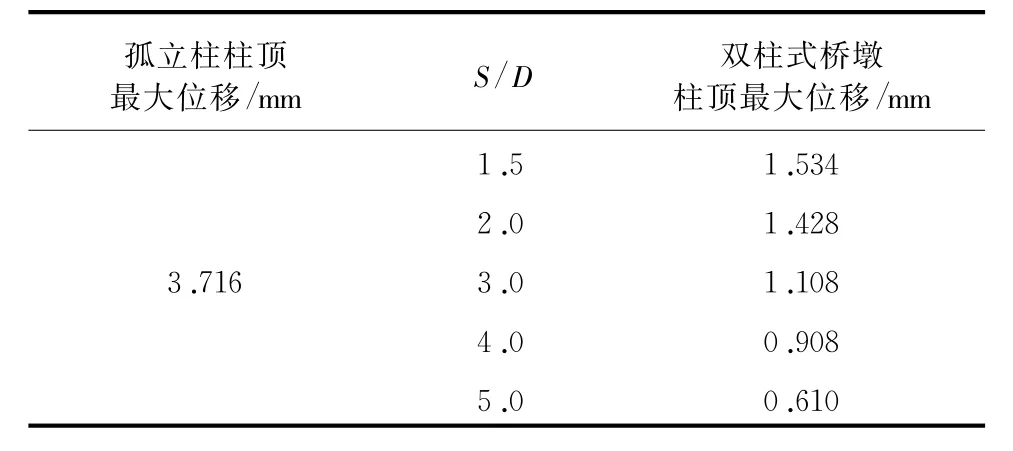
表2 结构在波浪荷载下的响应
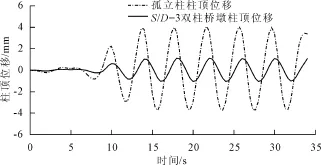
图7 柱顶位移曲线
由表2可以看出,双柱式桥墩因为顶端有盖梁的约束,使得桥墩整体刚度增加,顶端最大位移[20]较单柱结构明显减小;图7中可以看出结构的顶端位移随时间成周期性的正负振荡,与波面波动的周期相一致,这主要是由于波面的周期性波动对结构产生了往复的波浪力。
5 结 语
本文主要针对圆形截面双柱式桥墩在波浪场中受到的波浪力以及结构在波浪荷载作用下的响应进行数值仿真模拟,得到了在圆截面单柱结构波浪力的基础上双柱式结构波浪力数值取值,主要结论如下:
(1)双柱式桥墩的波浪力峰值不等于两柱波浪力峰值的简单叠加,必须考虑两柱之间相差的影响。
(2)在小柱距时,前柱和后柱干扰系数均随S/ D的增大而增大,当S/D≥4时,两柱干扰系数均趋于稳定,这与海港水文规范中所定义的群桩系数相一致。
(3)与过去认为的前柱波浪力一定大于后柱波浪力不同,由于后柱对前柱的抑制效应,后柱受到的波浪力是可以大于前柱的波浪力。
(4)在工程计算中,利用本文中的图5(a)、图5(b)、图5(c)以及单柱波浪力峰值,根据式(18)可以很容易求得双柱式桥墩中各柱的波浪力峰值以及整个桥墩的波浪力峰值。
(5)实际工程中柱距一般不会达到10 m,本文选取的S/D=5是为了得到干扰系数的变化规律。
[1] 左生荣.跨海大桥深水桥墩波浪效应研究[D].武汉:武汉理工大学,2013:1-13,47-57.
[2] 李 磊,张永亮.考虑动水压力效应的高桩承台连续梁桥抗震性能评估[J].水利与建筑工程学报,2015,13(4):28-32.
[3] Bushnell M J.Forces on cylinder arrays in oscillating flow[R].TX:Houston,OTC,1977.
[4] Sarpkaya T,Cinar M,Ozkaynak S.Hydrodynamic interference of two cylinders in harmonic flow[R].TX:Houston,OTC,1980.
[5] Chakrabarti S K.Wave forces on vertical array of tubes[C]//Civil Engineering in the Ocean Iv,ASCE,1979:241-259.
[6] 王爱群,徐立论.小直径组合桩的波浪力实验分析[J].海洋湖沼通报,2002,9(1):9-17.
[7] Xu Lilun,Wang Aiqun.Wave forces on arrays of vertical cylinders[J].Journal of Ocean University of QingDao,1991,21(1):1-13.
[8] 俞聿修,张宁川.双桩桩列上的不规则波浪力[J].大连工学院学报,1988,27(1):103-112.
[9] 俞聿修,史向宏.不规则波作用于群桩的水动力系数[J].海洋学报,1996,18(2):138-147.
[10] 李富荣.水-桩-土-桥墩结构体系的地震反应分析[J].水利与建筑工程学报,2008,6(2):47-51.
[11] 张新来.小尺寸双柱结构物上波流力的流固耦合数值分析[J].公路,2012,5(5):202-204.
[12] 邱大洪.波浪理论及其在工程中的应用[M].北京:高等教育出版社,1985:1-11,272-274.
[13] 杨 全.数值波浪模拟及其在海洋平台动态特性分析中的应用研究[D].镇江:江苏科技大学,2013:20-30.
[14] 李胜忠.基于FLUENT的二维数值波浪水槽研究[D].哈尔滨:哈尔滨工业大学,2006:17-35.
[15] 姚文伟.桩基结构物波浪力的工程计算方法[D].上海:上海交通大学,2009:9-12.
[16] 廖 瑾,亓路宽.小尺寸立柱水动力系数的数值分析[J].山西建筑,2011,37(26):181-182.
[17] 中华人民共和国交通运输部.海港水文规范[S].北京:人民交通出版社,2013:65-84.
[18] 韦诚勋.风-浪-流联合作用场数值模拟及其对圆柱构件的作用研究[D].哈尔滨:哈尔滨工业大学,2012:8-23,36-41.
[19] 雷欣欣.群桩在波浪作用下的水动力特性研究[D].大连:大连理工大学,2013:9-26.
[20] 柳春光,焦伟玲,张士博.基于能量平衡的桥梁结构抗震性能分析[J].水利与建筑工程学报,2016,14(2):61-66.
Numerical Analysis of Wave Force of a Small-scale Double Column Pier
LIU Chunguang1,2,LI Lulu1,ZHANG Shibo1
(1.Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China;2.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China)
The Morison formula is suitable to the calculation of wave forces on the isolated column with small diameter and can’t be used to double column pier.By defining the wave force interference coefficient,Morison formula can be used to solve the wave force of double column pier.This study adopts the linear wave theory and simulates linear wave by utilizing the push-pedal wave-generating method.By considering ANSYS Workbench as the data transfer platform between FLUENT and ANSYS,the numerical simulation about one-way FSI for wave forces on double-column pier in wave field were performed.The results show that interference coefficient of two columns’wave force approximate linearly increased with the increase of column distance within certain range.When exceed this range it tends to be stable.Because of the phase difference between two columns,the total interference coefficient of wave forces and the structure deformation of the double-column pier decreases with the increase of column distance.And these results can provide reference to wave load calculation of double column pier of the deep-water bridge in practical engineering.
Morison formula;linear wave;double column pier;FSI;structure deformation
U442.55
A
1672—1144(2016)05—0006—07
10.3969/j.issn.1672-1144.2016.05.002
2016-06-09
2016-07-04
国家重点基础研究发展计划资助“973计划”项目(2011CB013605-4);辽宁省优秀人才基金项目(2014020012);高等学校博士学科点博导专项科研基金项目(20130041110036)
柳春光(1964—),男,黑龙江牡丹江人,博士,教授,主要从事生命线地震工程及城市防灾减灾信息技术研究。
E-mail:liucg@dlut.edu.cn

