应用旋转矩阵的卫星姿态输出反馈机动控制

黄静， 刘刚， 刘付成， 李传江

1.上海航天控制技术研究所， 上海 201109 2.上海市空间智能控制技术重点实验室， 上海 201109 3.哈尔滨工业大学 航天学院， 哈尔滨 150001

应用旋转矩阵的卫星姿态输出反馈机动控制

黄静1,2,*， 刘刚1,2， 刘付成1,2， 李传江3

1.上海航天控制技术研究所， 上海 201109 2.上海市空间智能控制技术重点实验室， 上海 201109 3.哈尔滨工业大学 航天学院， 哈尔滨 150001

针对卫星姿态机动控制问题，提出一种只利用向量测量信息的无角速度反馈的输出反馈控制方法。卫星姿态的指向直接通过旋转矩阵进行描述，而不是先进行参数化过程，避免了由欧拉角、修正的罗德里格参数(MRPs)与四元数等姿态描述方式产生的奇异问题与退绕问题。首先，通过向量测量信息与一组期望姿态向量，引入一个新的姿态指向误差向量，并对其性质进行分析。其次，进一步结合主导滤波器的思想，设计了无需角速度信息的卫星姿态机动控制器，并应用Lyapunov理论，对闭环系统的全局稳定性进行了严格的证明。最后，对所提出的控制算法进行了数值仿真，其结果验证了所设计的输出反馈控制算法的可行性和有效性。

刚体卫星； 姿态机动； 旋转矩阵； 输出反馈； 向量测量

从20世纪末到现在，国内外的研究学者对刚体卫星姿态控制已经开展了广泛的研究，从任务需求出发，研究卫星姿态系统的稳定、机动与跟踪这3类控制问题，采用线性、非线性、自适应和鲁棒控制等控制方法完成高精度的指向控制及跟踪时变轨迹的姿态跟踪控制[1-6]。

在早期的研究中，由于考虑的是卫星姿态的稳定控制问题，姿态角度变化较小不会出现奇异问题，因此大部分都是基于直观的欧拉角的卫星姿态描述方式进行运动学建模和控制器的设计。接下来，人们开始研究卫星的大角度机动问题，为了解决姿态角度变化大可能出现的奇异问题，采用基于四元数或修正的罗德里格参数(MRPs)描述进行姿态控制器的设计[1-5]。但是，基于四元数或MRPs描述进行姿态控制时，在运动过程中会不可避免地出现退绕问题[6]，即初始姿态与期望姿态距离很近，但却沿着另一条不必要的路径大角度运动到期望姿态。

为了解决这个问题，近些年来，有些研究学者通过设计四元数偏差函数使得控制器具有抗退绕的能力[7]。进一步，为了简化控制器的设计，研究人员[8-11]开始研究直接使用星敏感器、太阳敏感器或磁强计等惯性测量元件得到的向量信息和陀螺仪等惯性器件得到的角速度信息，来直接进行反馈以对控制器进行设计，从而无需先根据测量信息进行四元数或MRPs参数化，再进行控制器的设计。通过向量信息直接得到刚体卫星的旋转矩阵，即秩为1的方向余弦矩阵，可以形成一个特殊的3×3的正交空间，记为SO(3)。文献[8]针对多输入拉格朗日系统的跟踪控制问题，应用几何流形理论，将系统误差映射到空间SO(3)，设计了PD形式的反馈与前馈控制器。Chaturvedi等[9]针对刚体的姿态稳定控制问题，应用旋转矩阵设计了连续时不变控制律，防止了其他姿态描述形式产生的复杂性与奇异性问题。文献[10]利用旋转矩阵设计了无需惯量信息的航天器姿态跟踪控制律，并证明了闭环系统是几乎全局稳定的。文献[11]应用特殊正交矩阵研究了刚体卫星姿态稳定与跟踪控制问题，并基于无源理论证明了所设计控制器的稳定性。Zheng和Song[12]研究了利用向量测量信息的多航天器姿态跟踪控制问题。

以上基于旋转矩阵进行卫星姿态的控制算法的研究都是需要卫星姿态角速度信息的，而在实际运行过程中，不可避免地会出现陀螺等惯性器件故障或测量信息不可知的情况。在过去的研究中，也有一些学者对无角速度测量信息的姿态控制进行过研究[13-15]。Lizarralde和Wen[13]应用四元数非线性滤波器代替角速度反馈信息的方法，针对机器人姿态控制问题设计了无需角速度信息的输出反馈控制器，并证明了系统的固有无源性。高岱等[14]研究了角速度不可测量时航天器的有限时间姿态控制问题，基于有限时间控制技术，分别针对单星系统与多星系统提出了由MRPs进行姿态描述的航天器输出反馈姿态控制算法。Zou等[15]针对含不确定性的航天器姿态系统，基于改进的Chebyshev神经网络理论设计了两种鲁棒自适应输出反馈控制器，采用非线性降阶观测器估计姿态四元数的导数，保证了闭环系统的一致有界稳定性。Benziane[16]基于融合惯性向量测量值，采用线性互补滤波器理论设计了姿态估计器，并将其应用于四旋翼飞行器的跟踪控制中。

但是对于直接采用向量测量信息而不经过姿态参数化的输出反馈控制的研究很少。而这类研究对于简化控制器设计、减少参数化过程可能出现的问题以及解决奇异与退绕现象是非常有益的。同时，无需角速度信息又在很大程度上增加了控制律的容错性与使用范围。因此，本文主要考虑只有向量测量信息的无角速度反馈的卫星姿态输出反馈机动控制问题。首先，应用一个特殊的向量代表姿态误差，并对其性质进行分析。进一步利用主导滤波器估计姿态角速度信息，将其引入到输出反馈控制器的设计中，最后通过稳定性证明和仿真结果可以看出此方法保证了闭环系统的全局稳定性，可以推广至其他姿态系统的控制器设计中，具有潜在的应用前景。

1 系统数学模型

1.1 刚体卫星动力学模型

考虑刚体卫星，卫星姿态动力学方程为[17]

(1)

(2)

在本文中，卫星姿态是利用特殊正交群SO(3)中的旋转矩阵进行描述的，即

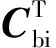
(3)

式中：Cbi∈SO(3)为本体坐标系相对于惯性坐标系的旋转矩阵，与轴/角参数{(a,φ)∈R3×R|aTa=1}的关系为

Cbi=Icosφ+(1-cosφ)aaT-a×sinφ

(4)

这样，利用Cbi，刚体卫星的姿态可以表示为

(5)

此方程也被称为泊松方程 (Poission’s equation)。

1.2 测量模型与姿态误差

在本文中，卫星上安装的姿态敏感器为星敏感器、磁强计或太阳敏感器等惯性敏感器的组合，能提供本体坐标系中至少两个非共线的姿态向量测量值。假设通过惯性敏感器得到的测量值是精确的且没有噪声的干扰。同时假设星上没有安装陀螺等角速度测量元件或角速度敏感器失效，即无法得到角速度信息。卫星在本体系中的姿态信息可以通过N个姿态测量向量计算得到

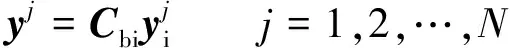
(6)

(7)

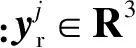
记第j个期望姿态信息与真实姿态信息的误差向量为

(8)

(9)

于是有

(10)

所有姿态误差的总和表示为

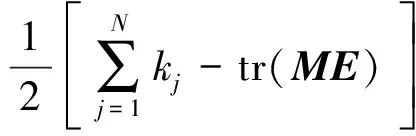
(11)

(12)

在2.3节的稳定性证明中将会用到这个性质。

1.3 研究目标

2 输出反馈控制器设计

2.1 指向误差及其性质

为了方便控制器的设计，首先引入一个新的状态误差r∈R3，定义为

(13)

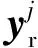
性质1在敏感器能提供本体坐标系中至少两个非共线的姿态向量测量值，即N≥2的条件下，当r=0时，可以推得E=I或tr(E)=-1。

证明：首先，通过(v×w)×=-vwT+wvT，化简r×可以得到

(14)

通过推导可以看出，当r=0时，r×=0，即ME=ETMT。由E的定义可知，E为一个实矩阵，那么它的特征值λk和特征向量ek满足：

(15)

(16)

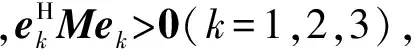
eig(E)=(1,cosθ+isinθ,cosθ-isinθ)

(17)

式中：θ为用轴/角参数表示的旋转角。由于E的所有特征值都为实数，那么θ=0°,±180°。此时E=I或tr(E)=-1，于是得到结论：当r=0时，可以推得E=I或tr(E)=-1。

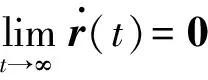
(18)

那么，

MEω=tr(ME)ω

(19)

在式(19)的两端均左乘ωTET，由于M=MT， 经过计算得到

tr(ME)ωTEω=tr(ME)ωTETω

(20)

此时，满足式(20)的有以下3种情况：①E=ET；② tr(ME)=0；③ω=0。首先分析第1种情况，当E=ET时，由性质1可知有E=I或tr(E)=-1。进一步分析当E=I时，有

(M-tr(M)I)ω=0

(21)

假设ω≠0，那么M=tr(M)I，由于tr(M)=λM1+λM2+λM3，λMi(i=1,2,3)为M的3个特征值，由M定义可知，当N≥3时，M的3个特征值均为正；当N=2时，M的特征值有一个为零，其他两个均为正值。此时M=tr(M)I是不成立的，因此第1种情况只能得到ω=0或tr(E)=-1的结论。

考虑第2种情况，当tr(ME)=0时，由式(19)可得

MEω=0

(22)

当N≥3时，M为正定的，那么此时可推得ω=0；当N=2时，由M和E的定义可将式(22)变化为

(23)

(24)

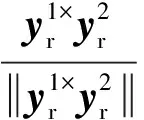
(25)

那么此时有

(26)

于是得到

(27)

应用等式

(28)

E=Icosθ+(1-cosθ)bbT-b×sinθ

(29)

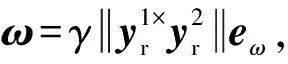
(30)

将式(30)代入式(27)并化简可以得到

(31)

进一步由式(10)可得

(32)

则将式(28)～式(30)代入式(32)并化简可以得到

(k1+k2)cosθ=0

(33)

由于k1+k2>0，那么cosθ=0，将其代入式(31)可得

(34)

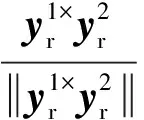
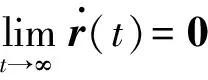
2.2 控制律设计

在全状态反馈控制器中，卫星的姿态和角速度信息全部都会被用到，而在输出反馈控制中，仅有姿态信息的反馈。控制器中所需的角速度信息需要通过其他途径进行模拟，主导滤波器便常用于对输入信号的微分进行估计。

首先，本文给出主导滤波器(LF)[19]的概念。主导滤波器本质上是一种非线性滤波器，如图1所示，对于任意状态量x∈R，其滤波方程为

(35)

由滤波方程式(35)可进一步得到主导滤波器的传递函数为

(36)

图1 主导滤波器示意图Fig.1 Sketch diagram of lead filter

本文以其旋转误差向量作为唯一反馈信息，并将其作为主导滤波器的输入，则相应的滤波方程为

(37)

(38)

由式(18)可知

(39)

在以上准备工作的基础上，本文给出了一个不需要角速度反馈的输出反馈卫星姿态控制器：

(40)

(41)

式中：kr为待设计的正常数。

2.3 稳定性证明

下面进行控制器式(40)的稳定性证明。

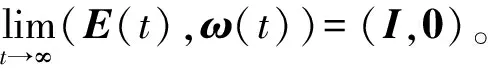
(42)

证明：考虑正定Lyapunov函数：

(43)

对式(39)求导，并将式(1)、式(39)和式(40)代入计算可得

ωT(-ω×Jω+u)+krωTr+

-2kρTρ≤0

(44)

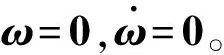
注1从控制器式(40)中可以看出，控制器中不含有与卫星转动惯量有关的量，即卫星在运动中转动惯量的变化对控制效果没有影响，提高了控制器的控制性能。

注2由于控制器式(40)是直接使用向量测量信息得到的，不存在四元数等描述方式会出现的退绕现象。

3 数学仿真分析

本节在MATLAB/Simulink环境下进行数值仿真实验，验证第2节提出的控制算法的有效性。

1) 仿真条件

假设卫星运行在太阳同步轨道，轨道高度为600 km，轨道倾角为δ=98°，则轨道坐标系相对于惯性坐标系的旋转矩阵Coi=C1(δ)，卫星绕滚动轴旋转98°。进一步假设N=3，卫星上装有3个惯性测量敏感器，能提供3个非共线的姿态向量，3个敏感器在惯性系下的观测单位向量分别为

且各敏感器的相对重要程度相同，即

k1=k2=k3=1

卫星转动惯量矩阵为

期望旋转矩阵为Cri=C2(45°)Coi，C2(45°)表示卫星沿俯仰轴旋转45°。

2) 初始条件

根据约束条件，控制参数选取为

kr=0.05,k=2

滤波器初始值选取为

在实际情况中，卫星在近地轨道受到的干扰力矩主要为重力梯度力矩和剩磁力矩，数量级大小约为10-5N·m，在本文中，假设干扰力矩为

为了进行对比说明输出反馈控制器的有效性，本文在参考文献[11]的基础上设计了基于旋转矩阵的全状态反馈卫星姿态机动控制器

us=-krr-kωω

(45)

经过稳定性证明，可以得出应用此PD控制器，刚体卫星姿态系统为渐近稳定的，在此不再详述。在仿真中，选取kr与输出反馈控制器相同，kω选取为1.2。

仿真结果如图2和图3所示，仿真时间为500 s。图2为采用本文提出的无角速度信息的输出反馈控制器的卫星姿态系统的仿真结果，其中图2(a)为标志卫星姿态机动误差的旋转角θ变化曲线，当θ=0°时，姿态误差为零；图2(b)为卫星姿态角速度ω随时间的变化曲线，可以看出，卫星姿态系统能够以较高的精度快速收敛到期望状态；图2(c)为卫星姿态三轴控制力矩u输出变化曲线，最大单轴输出力矩约为0.05 N·m，现有的飞轮等执行机构完全可以满足要求。

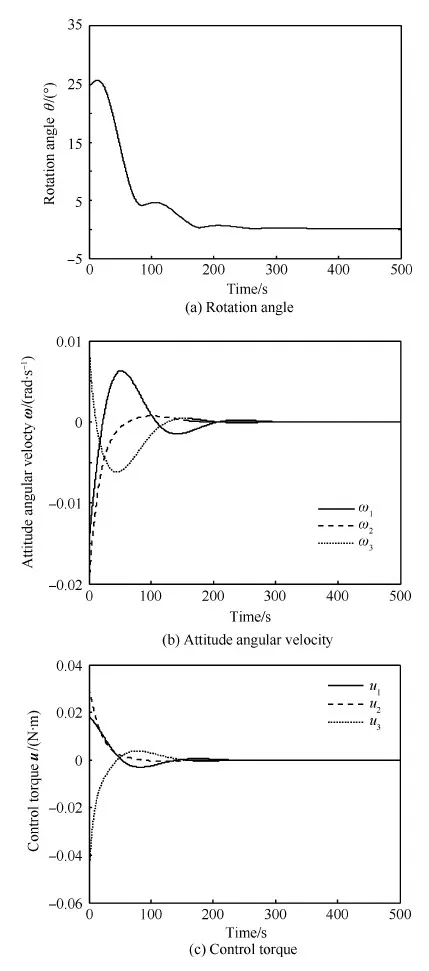
图2 输出反馈控制器下的卫星姿态仿真结果 Fig.2 Simulation results of satellite attitude with output feedback control law

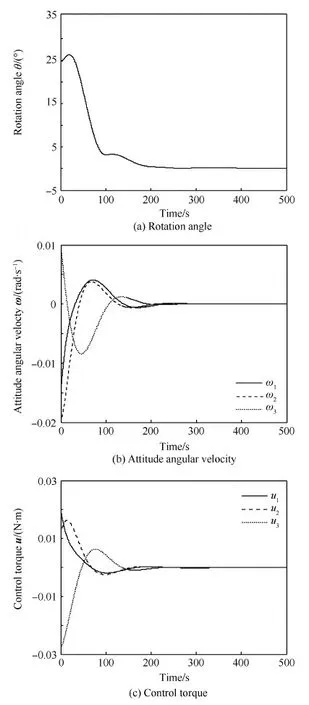
图3 全状态反馈控制器下的卫星姿态仿真结果Fig.3 Simulation results of satellite attitude with full-state feedback control law

图3为全状态反馈控制器的卫星姿态系统的仿真结果。其中图3(a)和图3(b)分别为标志卫星姿态机动误差的旋转角θ变化曲线和姿态角速度ω随时间变化曲线；图3(c)为卫星姿态三轴控制力矩u输出变化曲线。通过两组仿真结果对比可以看出，卫星姿态控制系统均能达到要求，且收敛时间与精度基本相同。但是在输出反馈控制器的仿真中，由于角速度信息需要通过滤波器近似，初始时需要一定时间收敛，因此初始时刻所需要的控制力矩要大于全状态反馈控制器，但是单轴最大输出力矩的数量级相同。仿真结果表明，即便加入外部干扰，采用本文提出的控制算法，卫星姿态闭环系统仍能稳定收敛，且与全状态反馈控制器的控制效果基本相同，充分验证了本文所提出的基于旋转矩阵的输出反馈控制器有效性。

4 结 论

本文直接利用卫星惯性传感器获得的向量测量信息，设计了一种无需角速度信息反馈的姿态控制律。

1) 提出的控制算法只需要两个非共线向量的测量值就能达到全局稳定的目标，且控制器结构简单，也不会受到运行过程中卫星转动惯量变化的影响，同时也不存在其他姿态描述方式带来的奇异问题与退绕问题，非常适合于实际卫星任务的应用，尤其是在传统陀螺等角速度传感器失效的情况。

2) 在今后的研究中，将在此基础上，考虑传感器噪声等对系统的影响，并针对姿态跟踪问题进行研究，以满足更多的任务需求。

[1] WIE B, BARBA P M. Quaternion feedback for spacecraft large angle maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(3): 360-365.

[2] JOSHI S M, KELKAR A G, WEN J T. Robust attitude stabilization of spacecraft using nonlinear quaternion feedback[J]. IEEE Transactions on Automatic Control, 1995, 40(10): 1800-1803.

[3] WEN J T, KREUTZ-DELGADO K. The attitude control problem[J]. IEEE Transactions on Automatic Control, 1991, 36(10): 1148-1162.

[4] TSIOTRAS P. Further passivity results for the attitude control problem[J]. IEEE Transactions on Automatic Control, 1998, 43(11): 1597-1600.

[5] EGELAND O, GODHAVN J M. Passivity based adaptive attitude control of a rigid spacecraft[J]. IEEE Transactions on Automatic Control, 1994, 39(4): 842-846.

[6] BHAT S P, BERNSTEIN D S. A topological obstruction to continuous global stabilization of rotational motion and the unwinding phenomenon[J]. Systems and Control Letters, 2000, 39(1): 63-70.

[7] 胡庆雷, 李理. 考虑输入饱和与姿态角速度受限的航天器姿态抗退绕控制[J]. 航空学报, 2015, 36(4): 1259-1266.

HU Q L, LI L. Anti-unwinding attitude control of spacecraft considering input saturation and angular velocity constraint[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1259-1266 (in Chinese).

[8] BULLO F, MURRAY R M. Tracking for fully actuated mechanical systems: A geometric framework[J]. Automatica, 1999, 35(1): 17-34.

[9] CHATURVEDI N A, SANYAL A K, MCCLAMROCH N H. Rigid body attitude control: Using rotation matrices for continuous, singularity-free control laws[J]. IEEE Control Systems, 2011,31(3): 30-51.

[10] SANYAL A, FOSBURY A, CHATURVEDI N, et al. Inertia-free spacecraft attitude tracking with disturbance rejection and almost global stabilization[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1167-1178.

[11] FORBES J R. Passivity-based attitude control on the special orthogonal group of rigid-body rotations[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1596-1605.

[12] ZHENG Z, SONG S M. Cooperative attitude tracking control for multiple spacecraft using vector measurements[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(13): 2375-2388.

[13] LIZARRALDE F, WEN J. Attitude control without angular velocity measurement: A passivity approach[J]. IEEE Transactions on Automatic Control, 1996, 41(3): 468-472.

[14] 高岱, 吕建婷, 王本利. 航天器有限时间输出反馈姿态控制[J]. 航空学报, 2012, 33(11): 2074-2081.

GAO D, LYU J T, WANG B L. Finite-time output feedback attitude control of spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2074-2081 (in Chinese).

[15] ZOU A M, KUMAR K D, HOU Z G. Quaternion-based adaptive output feedback attitude control of spacecraft using chebyshev neural networks[J]. IEEE Transactions on Neural Networks, 2010, 21(9): 1457-1471.

[16] BENZIANE L. Attitude estimation & control of autonomous aerial vehicles[D]. Versailles: Université de Versailles-Saint Quentin en Yvelines, 2015: 35-54.

[17] HUGHES P C. Spacecraft attitude dynamics[M]. 2nd ed. New York: Dover Publications, Inc., 2004: 93-129.

[18] MAHONY R, HAMEL T, PFLIMLIN J M. Nonlinear complementary filters on the special orthogonal group[J]. IEEE Transactions on Automatic Control, 2008, 53(5): 1203-1218.

[19] CACCAVALE F, VILLANI L. Output feedback control for attitude tracking[J]. Systems & Control Letters, 1999, 38(2): 91-98.

[20] KHALIL H K, GRIZZLE J W. Nonlinear systems[M]. 3rd ed. Upper Saddle River: Prentice-Hall, 2002: 111-133.

Outputfeedbackattitudemaneuvercontrolofsatelliteusingrotationmatrix

HUANGJing1,2,*,LIUGang1,2,LIUFucheng1,2,LIChuanjiang3

1.ShanghaiInstituteofSpaceflightControlTechnology,Shanghai201109,China2.ShanghaiKeyLaboratoryofAerospaceIntelligentControlTechnology,Shanghai201109,China3.SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001,China

Anoutput-feedbackattitudemaneuvercontrolstrategyintheabsenceofangularvelocityfeedbackisproposedforrigidsatellitesystembysolelyanddirectlyusingunit-lengthvectormeasurements.Theorientationofarigidbodyisdescribedbyarotationmatrixdirectly,ratherthanbyaparameterization,avoidingtheundesirablesingularproblemandunwindingphenomenoncausedbyEulerangle,quaternionorthemodifiedRodriguesparameters(MRPs)representationsoftheattitude.Aneworientationerroroftherigidbodyiscomputedbythevectormeasurementsandasetofdesiredvectormeasurements.Byusingtheleadfilter,thevelocity-freeattitudemaneuvercontrollawthatensuresset-pointregulationisdeveloped.WithintheLyapunovframework,theglobalstabilityoftheclose-loopsystemisguaranteed.Numericalsimulationresultsdemonstratethesuccessfulset-pointregulationoftheproposedoutput-feedbackcontrolstrategy.

rigidsatellite;attitudemaneuver;rotationmatrix;outputfeedback;vectormeasurements

2016-01-11；Revised2016-03-28；Accepted2016-04-06；Publishedonline2016-04-181458

URL：www.cnki.net/kcms/detail/11.1929.V.20160418.1458.002.html

NationalNaturalScienceFoundationofChina(61304005)

2016-01-11；退修日期2016-03-28；录用日期2016-04-06； < class="emphasis_bold">网络出版时间

时间：2016-04-181458

www.cnki.net/kcms/detail/11.1929.V.20160418.1458.002.html

国家自然科学基金 (61304005)

*

.Tel.：021-24183416E-mailhuangjing04415@163.com

黄静， 刘刚， 刘付成， 等． 应用旋转矩阵的卫星姿态输出反馈机动控制J． 航空学报,2016,37(12):3774-3782.HUANGJ,LIUG,LIUFC,etal.OutputfeedbackattitudemaneuvercontrolofsatelliteusingrotationmatrixJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3774-3782.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0114

V442.8

A

1000-6893(2016)12-3774-09

黄静女， 博士， 工程师。主要研究方向： 航天器姿态与轨道控制， 鲁棒控制， 最优控制。Tel.: 021-24183416E-mail: huangjing04415@163.com

刘刚男， 博士， 工程师。主要研究方向： 航天器姿态与轨道控制， 鲁棒控制， 非线性控制。Tel.: 021-24183245E-mail: unicorn1114@163.com

刘付成男， 博士， 研究员。主要研究方向： 航天器导航与控制。Tel.: 021-24183001E-mail: liufch@126.com

李传江男， 博士， 教授， 博士生导师。主要研究方向： 航天器姿态与轨道控制， 最优控制。Tel.: 0451- 86413411-8606E-mail: chuanjiangli@gmail.com

*Correspondingauthor.Tel.：021-24183416E-mailhuangjing04415@163.com