变几何涡轮叶栅叶端小翼的气动性能

高杰， 郑群， 刘鹏飞， 魏明

哈尔滨工程大学 动力与能源工程学院， 哈尔滨 150001

变几何涡轮叶栅叶端小翼的气动性能

高杰*， 郑群， 刘鹏飞， 魏明

哈尔滨工程大学 动力与能源工程学院， 哈尔滨 150001

针对大子午扩张变几何涡轮在可调静叶转动时旋转轴端严重恶化端区流场的问题，提出在可调静叶的机匣端部应用小翼结构的方法以克服这一问题并减少叶端间隙泄漏流动。应用数值方法和标准k-ω两方程湍流模型，并结合低速风洞试验，首先研究了可调静叶栅小翼端部流场及损失分布，并考虑了可调静叶转动的影响，随后给出了叶端凹槽状小翼结构，并评估了其气动性能以及对间隙变化的敏感性。研究结果表明：在可调静叶栅中应用叶端小翼不但可以避免可调静叶转动时旋转轴端恶化端区流场，还降低了叶端间隙泄漏驱动力，从而使得可调静叶在所有转角下都具有较好的端区流动性能，并且叶端小翼结合凹槽结构可以进一步减少间隙泄漏，总体上可调静叶栅总压损失系数降低了8.9%。

变几何涡轮； 小翼； 凹槽； 气动损失； 叶栅

变几何涡轮技术可以有效控制涡轮流量变化，进而调节和优化燃气轮机各部件之间的匹配关系，从而明显提高整个燃气轮机机组的加、减速特性和低工况性能[1]，因此开展变几何涡轮技术方面的研究有着十分重要的实际意义和工程应用价值。

变几何涡轮在航空、舰船、机车和坦克燃气轮机上已得到广泛应用，对于涡轮变几何对其效率的影响亦有很多研究。Moffitt等[2]试验研究了可调静叶转角对单级涡轮的影响。研究结果显示，在不同的膨胀比下，不管是打开还是关闭可调静叶，涡轮效率皆有明显降低，可调静叶打开时涡轮效率下降了1%，而可调静叶关闭时却下降了大概5%。

变几何涡轮在许多应用场合下都是以多级形式存在，这增加了变几何涡轮试验的难度，并且成本也比较高。宋力强和王永泓[3]根据传统的定几何燃气轮机损失模型，提出了在变几何条件下，如何进行涡轮损失计算的思路，并给出了一套完整的计算变几何涡轮损失的方法。Qiu等[4]提出了一种预测变几何涡轮稳态特性的小偏差方法，预测结果表现出了与现有试验数据[2]很好的一致性。

需要注意的是，应用变几何涡轮，一定不能使得可能获得的效益被变几何时造成的涡轮效率下降所抵消。因此，除了要弄清楚涡轮变几何对其性能的影响之外，还要充分了解影响这一效率的各种因素，以便能把由此引起的性能恶化降到最低程度。Razinsky和Kuziak[5]发现，涡轮变几何后，必须在静叶端部留有一定的间隙高度，以保证静叶的自由转动，这样就会引起静叶端部的附加损失，导致涡轮效率下降。

刘顺隆和冯永明等[6-7]对某型船用燃气轮机动力涡轮可调导叶级的流场结构以及大攻角流动特性进行分析，提出可调导叶宜采用较小转折角的后部加载叶型，而可调导叶级动叶栅要采用较大负攻角的气动设计原则。Yue等[8]数值研究了柱面端壁和球面端壁下的变几何涡轮流场，结果显示在可调静叶端部，泄漏涡与通道涡之间存在相互干扰，带来了附加的掺混损失，并且局部球面端壁的采用在结构上对端部间隙设计进行优化，从而提高了涡轮效率。陈升等[9]利用叶栅试验和损失模型分析相结合的方法对变几何平面叶栅出口流场进行了研究。马超等[10]对某变几何涡轮在不同导叶转角工况下的流场进行了Particle Image Velocimetry (PIV)试验研究，获得了动叶叶栅流道及其下游区域详细的流场及涡量场数据，并进行了对比分析。在此基础上，也有研究人员致力于可调静叶端区泄漏损失控制方法的研究，比如潘波等[11]在可调导叶上下端壁增加圆盘设计，这明显减小了导叶端壁间隙对涡轮气动性能的影响。

现代燃气轮机气动涡轮一般都是大子午扩张设计，对于这种类型涡轮进行变几何设计时，一般需要在端部给定较大的间隙以保证可调静叶在整个转角范围内都不被卡死，这必然会带来较高的端区损失。为此，Gao等[12]提出台阶型球面端壁概念，并对某型大子午扩张船用动力涡轮进行变几何设计。结果显示，所设计的变几何涡轮在设计点下达到了固定几何涡轮的效率水平。尽管如此，由于对大子午扩张端壁进行了较大改动，最终效果如何还有待于试验验证。

国内外学者针对叶顶间隙泄漏流动已进行了广泛的研究，并进一步提出了许多控制间隙泄漏损失的方法，包括凹槽叶顶[13-15]、叶顶小翼[16- 17]、叶顶喷气[18-19]等。然而截至目前，有关变几何涡轮可调静叶端部间隙泄漏损失控制的研究还比较少，尤其是针对真实大子午扩张变几何涡轮可调静叶端区流动损失控制的研究还尚未见公开报道，而这也正是本文所要开展的工作。

1 问题的提出

图1为某型燃气轮机的大子午扩张变几何动力涡轮，其调节系统具体参见文献[20]。从图1中可以看出，该变几何涡轮的子午扩张角较大，尤其是在静叶机匣部分。

图2给出了-6° 和8° 转角下可调静叶片端部位置的情况，可以明显看出，当可调静叶关闭(-6°)时，在静叶片吸力侧顶部前侧，旋转轴端凸出于机匣，而在顶部后侧，旋转轴端则有所凹陷；而在静叶片压力侧顶部的大部分区域，旋转轴端则几乎陷入机匣内侧，形成较大的凹陷(图中未给出)，不管是凸起或者凹陷皆对端区流动产生干扰，并且随着旋转角度的增加而更加明显，从而恶化端区流动。同样地，当可调静叶打开(8°)时，则在可调静叶片压力侧顶部形成凸起，而在吸力侧顶部形成凹陷，同样对端区流动产生了明显干扰。

图1 大子午扩张变几何涡轮示意图 Fig.1 Schematic of a high-endwall angle variable-geometry turbine

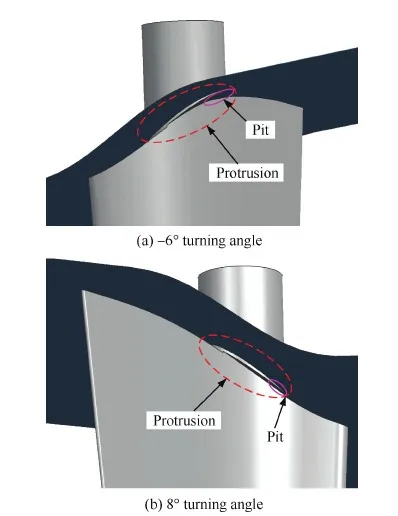
图2 -6° 和8° 转角下静叶片端部位置示意图Fig.2 Schematic of vane-end position at turning angles of -6° and 8°

基于以上分析可以看出，对于大子午扩张变几何涡轮，不管可调静叶是打开还是关闭，旋转轴端皆对端区流动产生了明显干扰，带来较强的二次流动。并且，对于大子午扩张变几何涡轮，一般需要在可调静叶片端部给定较大的间隙，而这必然带来较强的泄漏流动，从而使得端区流动变得尤为复杂。

2 可调静叶模型及叶端小翼结构

针对大子午扩张变几何涡轮在可调静叶转动时旋转轴端严重恶化端区流场的问题，本文提出在可调静叶的机匣端部应用小翼结构，使得旋转轴端成为流道的一个组成部分，从而克服这一结构性问题，并寻求减少叶端间隙泄漏流动。为此，针对某低速试验用可调平面叶栅展开数值与试验验证研究。

初步设计的叶端带有小翼结构的可调静叶栅如图3(b)所示，图3(a)为原型可调静叶栅，以用于对比研究。如图3所示，叶端小翼宽度沿顶部叶型为等厚度分布，为了确保顶面可以完全包含旋转轴端，初步给定其宽度为5 mm。另外，以45° 方向将小翼与静叶片进行倒圆角连接。可以看出，扩展出的小翼结构参数相对于叶栅节距而言是一个较小的值，并不影响实际安装。

需要说明的是，本文针对可调平面叶栅的小翼结构并不是最佳的结果，只是对上述新想法进行验证。大子午扩张变几何涡轮叶端小翼结构的具体形式一方面应避免旋转轴转动带来的干扰端区流动的问题，另一方面应以对调节干扰较小为基本前提。

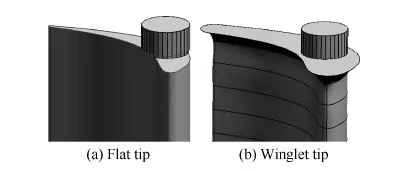
图3 研究的可调静叶片端部结构示意图 Fig.3 Schematic of investigated variable vane-end geometries

3 试验装置与测量方法

变几何涡轮叶栅低速风洞试验在哈尔滨工程大学低速平面叶栅风洞上进行，如图4所示。来流由一台额定功率为560 kW电机带动的轴流风机提供，其中电机与压气机的变速比为1∶24。风洞试验段出口尺寸为90 mm×240 mm。试验叶栅由5片叶片(仅一端带有间隙和旋转轴，叶高为90 mm)组成，其中旋转轴位于叶片50%轴向弦长位置，其直径为19 mm。栅前总压、总温分别由栅前总压探针和热电偶测得。叶栅出口截面气动参数测量采用五孔探针及非对向测量法，出口截面位于叶片尾缘下游40%轴向弦长位置。试验中还对型面静压分布、机匣端壁静压分布进行了测量。表1给出了可调试验叶栅的几何和气动参数。对于本文试验风洞测量系统，五孔探针测量总压的不确定度小于1%，热电偶测量总温的不确定度为0.5 ℃，气流角误差为1°。

图4 风洞及测量平面位置示意图 Fig.4 Schematic of wind tunnel and position of measurement planes

表1可调静叶栅几何参数及边界条件

Table1Geometricalparametersandboundaryconditionsofvariablevanecascades

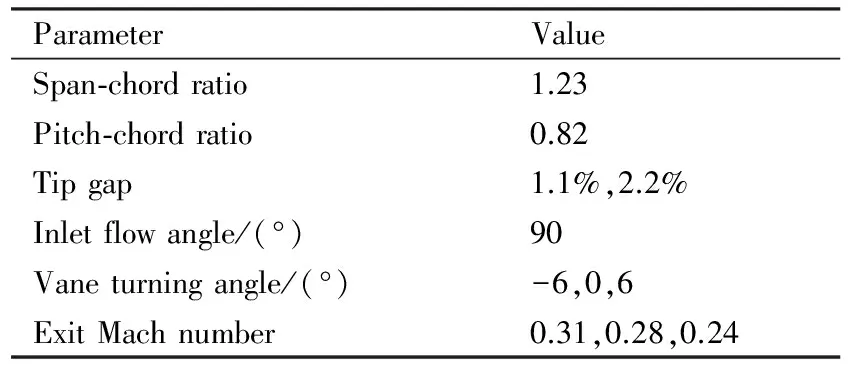
ParameterValueSpan⁃chordratio1．23Pitch⁃chordratio0．82Tipgap1．1%，2．2%Inletflowangle/(°)90Vaneturningangle/(°)-6，0，6ExitMachnumber0．31，0．28，0．24

4 数值计算方法

4.1 计算模型

可调静叶计算模型采用ANSYS CFX 11.0商用软件求解定常可压缩雷诺平均Navier-Stokes方程组，借助有限体积法离散控制方程以及标准k-ω两方程湍流模型封闭方程组。离散格式为二阶迎风格式，总体计算精度为二阶。

本文可调静叶计算域与试验平面叶栅保持一致，即可调叶栅仅上端带有间隙和旋转轴，其下端面为对称边界。

可调静叶计算域如图5所示。可调静叶计算网格由NUMECA软件包的Autogrid5与IGG模块生成。为了考虑叶端部分间隙的影响，首先采用蝶形网格拓扑结构生成完全间隙的网格，然后沿流向切割网格，并根据部分间隙的结构形式调整优化其余间隙网格。为改善网格质量，叶片表面采用O型网格，进出口及主流区采用H型网格。沿间隙高度方向上布置33个网格节点。旋转轴与主流区等网格不匹配区域采用交界面连接来传递数据。壁面第一层网格的平均y+值小于1，最大值为3左右。经网格敏感性验证确定本文针对原型可调静叶与叶端带有小翼的可调静叶的网格数分别为109万与124万。

另外，计算域进出口边界条件均在绝对坐标系下给定：进口给定总温、总压和进气角(轴向进气)，出口给定背压，固壁给定绝热无滑移边界条件。由于未进行试验湍流强度测定，进口湍流强度暂定为5%。本文计算工质为定比热理想空气。

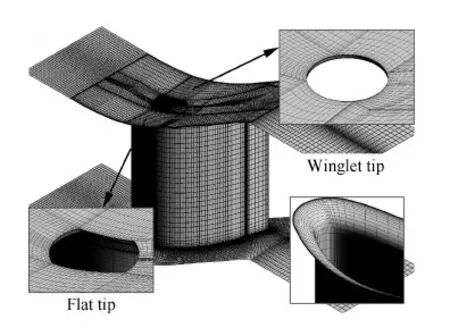
图5 三维计算网格Fig.5 Three-dimensional computational grids

4.2 数值与试验结果对比

为验证数值计算方法的可靠性，首先对原型可调静叶进行数值计算，并与试验结果进行比较。不同转角下试验叶栅中间叶高压力系数Cp分布的数值(CFD)与试验(Test)结果对比如图6所示，图中z/ca代表相对轴向弦长，从图中可以看出，在所有转角下，数值预测结果皆与试验值比较吻合。

此外，与来流攻角对叶片负荷影响不同的是，可调静叶转动不仅改变了叶片负荷分布，还改变了其大小。在0° 转角下，可调静叶最低压力点在轴向弦长70%位置左右，其属于“后部加载”叶型。随着可调静叶关闭，叶片负荷增加，并且最大负荷位置移向叶片尾缘，叶片负荷的后加载程度加深。此时，旋转轴对间隙泄漏的阻塞效果减弱。整体上，由于叶片负荷增加以及负荷后移等原因，叶端间隙泄漏会有明显增加。而随着可调静叶打开，叶片负荷有明显减小，并趋于“均匀加载”，而这则会减少叶端间隙泄漏流动及泄漏损失。

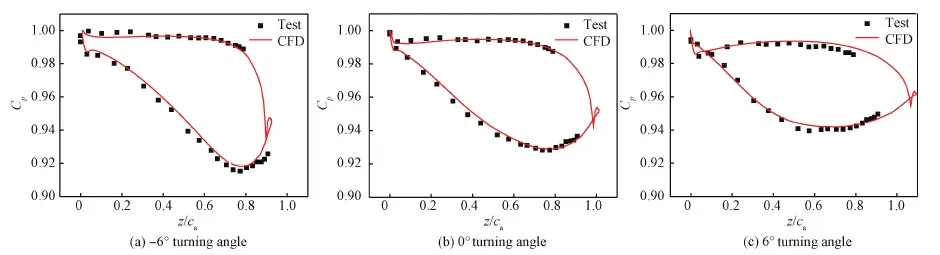
图6 不同转角下叶片中间叶高压力系数分布Fig.6 Midspan pressure coefficient distributions along the vane surface at different turning angles

5 数值计算结果和分析

为方便研究，首先给出总压损失系数Cpt的定义为

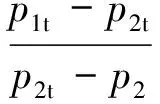
(1)

式中：p1t、p2t分别为叶栅进、出口总压；p2为叶栅出口静压。需注意的是，本文数值计算是在真实的动力涡轮出口马赫数工况下开展的，其中设计点马赫数为0.44。

5.1 可调静叶小翼端部流场及损失分布

图7 叶端流线及机匣压力系数分布Fig.7 Streamlines patterns over the vane-end overlay with casing pressure coefficient distributions

可调静叶的端部结构形式使得端部存在部分间隙以及由此引起的间隙泄漏流动。图7给出了0° 转角下叶端带有小翼的可调静叶及原型静叶的端部流线及机匣压力系数分布。旋转轴的存在减小了周向泄漏面积，从而对间隙泄漏起到一定的阻塞作用。另外，旋转轴将间隙泄漏流动分为2股：旋转轴前侧的间隙泄漏流动较弱，这主要是由于较小的横向压力梯度所致；而在旋转轴后侧，由于横向压力梯度较大，使得间隙泄漏流动比较强。由此可以看出，旋转轴后侧是叶端间隙泄漏的主要区域。

从图7叶端流线及静压分布上也可以看出，沿流线方向，在旋转轴后侧存在一个低速回流区。考虑到旋转轴附近的流线方向与主要泄漏流动方向呈斜交状，由此可以推测出，旋转轴绕流效应与间隙泄漏流动之间存在比较明显的干扰。随后，泄漏流流出叶端间隙，间隙泄漏涡核形成，而旋转轴前侧的泄漏流则围绕着泄漏涡核形成泄漏涡。

通过比较图7(a)与图7(b)可以看出，叶端带有小翼使得旋转轴后侧的低压区域向尾缘移动；并且，叶端带有小翼也使得低压区域变大，不过，间隙压力侧静压值有所减小，而吸力侧压力值则有明显增加，整体上叶端横向压力梯度得到降低，这可以从图8叶端小翼对近端部负荷分布的影响中得到证实。

从图8中也可以看出，旋转轴绕流效应对近端部的负荷分布形式产生了明显影响。尤其是在近间隙吸力侧，在旋转轴前侧附近，由于气流绕流旋转轴的影响，近端部压力急剧降低；在绕流旋转轴的过程中，近端部压力也有小幅波动；在旋转轴后侧，由于低速回流区的存在又使得近端部压力突然降低。

图8 叶端小翼对近端部负荷分布的影响 Fig.8 Effect of vane-end winglet on vane loading distribution near the vane-end

叶端带有小翼则使得近叶端间隙压力侧和吸力侧的静压变化比较平滑，明显减小了旋转轴绕流效应的影响，并且近叶端负荷也有明显减小，这在一定程度上减小了间隙泄漏驱动力以及间隙泄漏流动。

以上分析也可以从2种叶端结构的70%轴向弦长位置截面马赫数对比分布中得到证实，如图9所示，其中右侧为吸力侧。由于叶端小翼结构明显减少了近叶端负荷，间隙内的泄漏射流速度也随之降低，并且间隙吸力侧泄漏涡所在的低速区范围也有明显减小。

图9 70%轴向弦长位置截面马赫数分布Fig.9 Mach number distributions on the cut plane at 70% axial chord

从图10可调静叶栅内熵增轮廓图中可以明显看到，在第4个截面也即旋转轴前侧之前区域，间隙泄漏引起的损失区范围及峰值并无明显变化，而在此之后，间隙泄漏损失有明显降低，尤其是在最后2个截面区域。

图10 可调静叶栅内熵增轮廓图 Fig.10 Entropy-increase contours in a variable vane cascade

5.2 可调静叶转动的影响

可调静叶转动改变了静叶喉部面积，这不仅改变了叶片负荷分布及其大小，还对叶栅通道损失以及与下游叶片列之间的匹配产生了重要影响。图11给出了不同转角下可调静叶栅总压损失系数对比。可调静叶关闭明显增加了通道损失，而可调静叶打开却减少了通道损失。此外，叶端带有小翼使得在所有转角下静叶通道损失都有明显降低。

图11 不同转角下可调静叶总压损失系数对比Fig.11 Comparison of variable vane total pressure loss coefficients at different turning angles

图12给出了2种叶端结构在不同转角下的节距平均出气角α沿相对叶高x/h的分布。正如前人研究结果所指出的那样，可调静叶关闭减小了出气角，而可调静叶打开则增加了出气角，这满足了变几何涡轮调节工况的需求。从图12中还可以看出，在所有转角下，叶端带有小翼皆明显降低了静叶端部的气流欠偏转程度，尤其是在-6° 转角下降低效果更为明显。

图12 不同转角下节距平均出气角沿叶高分布 Fig.12 Spanwise pitch-averaged outlet flow angle distributions at different turning angles

5.3 叶端凹槽状小翼结构及其性能

正如上文所述，可调静叶旋转轴后侧间隙是叶端间隙泄漏的主要区域。并且对于舰船燃机来说，其在寿命期90%以上的时间都处于部分负荷工况下运行，这意味着可调静叶将长期处于关小或者关闭状态下运行，而这也进一步使得旋转轴后侧间隙成为主要的间隙泄漏区域。为了进一步减小可调静叶端部间隙泄漏流动，本文尝试在叶端小翼基础上设置凹槽结构，以在减小间隙泄漏驱动力的基础上进一步增加泄漏流动阻力，从而明显减小间隙泄漏损失。

初步设计的可调静叶叶端凹槽状小翼结构如图13所示。在可调静叶旋转轴前后侧分别设置凹槽结构，其中凹槽肩壁宽度、深度分别为1.4 mm 和1.8 mm。

图14给出了不同叶端结构下节距平均总压损失系数沿叶高分布，其中叶端间隙为1 mm。正如所假设那样，叶端凹槽状小翼结构在小翼结构基础上进一步减小了间隙泄漏损失。

图15给出了可调静叶在不同叶端结构下的总压损失系数随间隙τ的变化曲线。从图中可以看出，在叶端间隙分别为1 mm和2 mm下，叶端小翼结构和凹槽状小翼结构皆减少了可调静叶出口总压损失系数，凹槽状小翼结构下的损失更小，可调静叶总压损失系数最大降低了8.9%。不过，2种结构在不同间隙下对通道损失的控制效果却是不一样的。从图15中可以看出，叶端小翼结构增加了可调静叶性能对间隙变化的敏感性，而叶端小翼结合凹槽结构以后，则降低了对间隙变化的敏感性，并且使得可调静叶性能对间隙变化的敏感性与原型相当。

图13 可调静叶端部凹槽状小翼结构Fig.13 Variable vane-end cavity-winglet structure

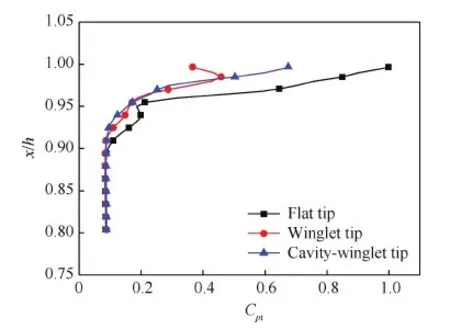
图14 不同叶端结构下节距平均总压损失系数沿叶高分布Fig.14 Spanwise pitch-averaged total pressure loss coefficient distributions for different vane-end structures

图15 不同叶端结构总压损失系数随间隙变化曲线Fig.15 Change curves of total pressure loss coefficient with clearance for different vane-end structures

6 结 论

1) 在可调静叶栅中应用叶端小翼不但避免了可调静叶转动时旋转轴端恶化端区流场的问题，还降低了叶端间隙泄漏流动的驱动力，从而使得可调静叶在所有转角下都具有较好的端区流动性能。

2) 叶端小翼结合凹槽结构可以进一步减少可调静叶端部间隙泄漏流动，可调静叶总压损失系数最大可降低8.9%。

3) 虽然叶端小翼结构增加了可调静叶性能对间隙变化的敏感性，但结合凹槽结构以后，其敏感性与原型相当，从而使得叶端凹槽状小翼结构适用于大子午扩张变几何涡轮。

本文研究工作可为针对真实大子午扩张变几何涡轮可调静叶的顶部结构设计提供参考，以期改善真实大子午扩张变几何涡轮可调静叶的变工况性能。

[1] KARSTENSEN K W, WIGGINS J O. A variable-geometry power turbine for marine gas turbines[J]. Journal of Turbomachinery, 1990, 112(2): 165-174.

[2] MOFFITT T P, WHITNEY W J, SCHUM H J. Performance of a single-stage turbine as affected by variable stator area： AIAA-1969-0525[R]. Reston: AIAA, 1969.

[3] 宋力强, 王永泓. 变几何燃气涡轮损失模型的分析[J]. 燃气轮机技术, 2004, 17(2): 35-40.

SONG L Q, WANG Y H. Analysis on the loss model of variable geometry turbines[J]. Gas Turbine Technology, 2004, 17(2): 35-40 (in Chinese).

[4] QIU C, SONG H F, WANG Y H, et al. Performance estimation of variable geometry turbines[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009, 223(4): 441-449.

[5] RAZINSKY E H, KUZIAK W R. Aerothermodynamic performance of a variable nozzle power turbine stage for an automotive gas turbine[J]. Journal of Engineering for Gas Turbines and Power, 1977, 99(4): 587-592.

[6] 刘顺隆, 冯永明, 刘敏, 等. 船用燃气轮机动力涡轮可调导叶级的流场结构[J]. 热能动力工程, 2005, 20(2): 120-124.

LIU S L, FENG Y M, LIU M, et al. The flow field structure of the power-turbine variable-area nozzle stage of a marine gas turbine[J]. Journal of Engineering for Thermal Energy and Power, 2005, 20(2): 120-124 (in Chinese).

[7] 冯永明, 刘顺隆, 刘敏, 等. 船用燃气轮机变几何动力涡轮大攻角流动特性的三维数值模拟[J]. 热能动力工程, 2005, 20(5): 459-463.

FENG Y M, LIU S L, LIU M, et al. Three-dimensional numerical simulation of the flow characteristics at a large incidence of the variable-geometry power turbine of a marine gas turbine[J]. Journal of Engineering for Thermal Energy and Power, 2005, 20(5): 459-463 (in Chinese).

[8] YUE G Q, YIN S Q, ZHENG Q. Numerical simulation of flow fields of variable geometry turbine with spherical endwalls or nonuniform clearance: GT2009-59737[R]. New York: ASME, 2009.

[9] 陈升, 邱超, 宋华芬. 涡轮平面叶栅变几何试验研究[J]. 热能动力工程, 2011, 26(1): 7-12.

CHEN S, QIU C, SONG H F. Variable geometry experimental study of a turbine plane cascade[J]. Journal of Engineering for Thermal Energy and Power, 2011, 26(1): 7-12 (in Chinese).

[10] 马超, 臧述升, 黄名海. 变几何涡轮动叶栅流场的PIV实验研究[J]. 动力工程学报, 2014, 34(6): 458-462.

MA C, ZANG S S, HUANG M H. PIV flow field measurement for rotor blade cascade of a variable geometry turbine[J]. Journal of Chinese Society of Power Engineering, 2014, 34(6): 458-462 (in Chinese).

[11] 潘波, 陶海亮, 赵洪雷, 等. 可调导叶端壁间隙泄漏损失控制方法研究[J]. 工程热物理学报, 2013, 34(4): 618-623.

PAN B, TAO H L, ZHAO H L, et al. Investigation on the control strategy of variable guide vane endwall gap leakage loss[J]. Journal of Engineering Thermophysics, 2013, 34(4): 618-623 (in Chinese).

[12] GAO J, ZHENG Q, YUE G Q, et al. Variable geometry design of a high endwall angle power turbine for marine gas turbines: GT2015-43173[R]. New York: ASME, 2015.

[13] MISCHO B, BURDET A, ABHARI, et al. Influence of stator-rotor interaction on the aerothermal performance of recess blade tips: GT2008-50496[R]. New York: ASME, 2008.

[14] EL-GHANDOUR M, MORI K, NAKAMURA Y. Desensitization of tip clearance effects in axial flow turbines[J]. Journal of Fluid Science and Technology, 2010, 5(2): 317-330.

[15] 高杰, 郑群. 叶顶凹槽形态对动叶气动性能的影响[J]. 航空学报, 2013, 34(2): 218-226.

GAO J, ZHENG Q. Effect of squealer tip geometry on rotor blade aerodynamic performance[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 218-226 (in Chinese).

[16] COULL J D, ATKINS N R, HODSON H P. Winglets for improved aerothermal performance of high pressure turbines[J]. Journal of Turbomachinery, 2014, 136(9): 091007-1-091007-11.

[17] LEE S W, KIM S U, KIM K H. Aerodynamic performance of winglets covering the tip gap inlet in a turbine cascade[J]. International Journal of Heat and Fluid Flow, 2012, 34: 36-46.

[18] GAO J, ZHENG Q, ZHANG Z Y, et al. Aero-thermal performance improvements of unshrouded turbines through management of tip leakage and injection flows[J]. Energy, 2014, 69: 648-660.

[19] NIU M S, ZANG S S. Experimental and numerical investigations of tip injection on tip clearance flow in an axial turbine cascade[J]. Experimental Thermal and Fluid Science, 2011, 35(6): 1214-1222.

[20] 刘宇, 闫锦生, 卫嘉, 等. 燃气轮机动力涡轮可转导叶系统： ZL202348444U[P]. 2012-07-25.

LIU Y, YAN J S, WEI J, et al. Variable-geometry vane system for gas turbine power turbines: China: ZL202348444U[P]. 2012-07-25 (in Chinese).

Aerodynamicperformanceofavariablegeometryturbinecascadeusingavane-endwinglet

GAOJie*,ZHENGQun,LIUPengfei,WEIMing

CollegeofPowerandEnergyEngineering,HarbinEngineeringUniversity,Harbin150001,China

Inahighendwall-anglevariable-geometryturbine,therotatingshaftendcanleadtoaseriousdeteriorationofendwallflowfieldswhenthevariablevanerotates.Awingletisproposedtobeappliedtothevariablevanecasing-endtoovercomethisproblemandthenreducethevane-endleakageflow.Combinedwiththelow-speedwindtunneltest,numericalinvestigationisperformedbysolvingReynolds-averagedNavier-Stokesequationsinconjunctionwithastandardk-ωtwo-equationturbulencemodel.Theendwallflowfieldsandlossdistributionofthevariablevanewithwingletsareanalyzed.Theeffectsofvaneturningarediscussed.Thevane-endcavity-wingletstructureisthenproposed,andtheaerodynamicperformanceanditssensitivitytovane-endclearanceheightareevaluated.Theresultsshowthatthevariablevanewithwingletscannotonlyavoidthedeteriorationofendwallflowfieldscausedbyvaneturning,butalsoreducethevane-endclearanceleakagedrivingforce,thusleadingtoimprovedendwallflowperformanceofvariablevanesatallturningangles.Besides,thevariablevanewithcavity-wingletscanfurtherreducetheleakageflow,andthetotalpressurelosscoefficientisreducedoverallby8.9%ascomparedtothebaseline.

variablegeometryturbine;winglettip;cavitytip;aerodynamicloss;cascade

2015-12-17；Revised2016-04-20；Accepted2016-04-29；Publishedonline2016-05-051543

URL：www.cnki.net/kcms/detail/11.1929.V.20160505.1543.006.html

s：NationalNaturalScienceFoundationofChina(51406039)；NaturalScienceFoundationofHeilongjiangProvinceofChina(QC2016059)

2015-12-17；退修日期2016-04-20；录用日期2016-04-29； < class="emphasis_bold">网络出版时间

时间：2016-05-051543

www.cnki.net/kcms/detail/11.1929.V.20160505.1543.006.html

国家自然科学基金(51406039)；黑龙江省自然科学基金(QC2016059)

*

.Tel.：0451-82518116E-mailgaojie_d@hrbeu.edu.cn

高杰， 郑群, 刘鹏飞, 等． 变几何涡轮叶栅叶端小翼的气动性能． 航空学报,2016,37(12):3615-3624.GAOJ,ZHENGQ,LIUPF,etal.Aerodynamicperformanceofavariablegeometryturbinecascadeusingavane-endwinglet.ActaAeronauticaetAstronauticaSinica,2016,37(12):3615-3624.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0139

V231.3

A

1000-6893(2016)12-3615-10

高杰男， 博士， 副教授， 硕士生导师。主要研究方向： 叶轮机械气动热力学。Tel.: 0451-82518116E-mail: gaojie_d@hrbeu.edu.cn

*Correspondingauthor.Tel.：0451-82518116E-mailgaojie_d@hrbeu.edu.cn