滚转弹两框架导引头的前馈补偿技术

刘晓， 莫波,*， 刘福祥， 闫新颖

1.北京理工大学 宇航学院， 北京 100081 2.北京航天自动控制研究所， 北京 100854

滚转弹两框架导引头的前馈补偿技术

刘晓1， 莫波1,*， 刘福祥1， 闫新颖2

1.北京理工大学 宇航学院， 北京 100081 2.北京航天自动控制研究所， 北京 100854

针对弹体滚转情况下两框架平台式导引头的伺服控制问题，基于导引头运动学和动力学，建立了导引头稳定回路模型。结合弹体滚转条件下的导引头输入指令和输出视线角速率关系，构建了视线闭环回路。针对偏航、俯仰通道间的解耦控制问题，推导出解耦条件，要求两通道由失调角到光轴转动角速度的传递函数相同。仿真分析了该模型在视线角输入以及弹体姿态扰动输入时，弹体滚转对导引头跟踪精度产生的影响，并由此提出了滚转角速度前馈补偿控制方案。结果表明，采用结合滚转角前馈补偿控制的两框架平台式导引头方案可以满足滚转弹的制导精度要求。

导引头； 伺服机构； 弹体滚转速率； 跟踪精度； 前馈控制

导引头具有搜索、识别和捕获目标的功能，是制导回路的测量敏感元件，为制导系统提供目标相对导弹在俯仰、偏航方向的运动信息[1]。滚转弹上大多采用三框架平台式导引头，其优点是可以隔离弹体在偏航、俯仰和滚转3个方向上的扰动，缺点是结构复杂、体积较大；非滚转弹上大多采用两框架平台式导引头，其优点是控制简单、尺寸小，缺点是无法隔离弹体在滚转方向的扰动。对于外形尺寸限制严格的滚转弹而言，三框架平台式导引头与导弹有限的安装空间之间存在较为突出的矛盾，将两框架平台式导引头应用在滚转弹上可以减小弹径需求，简化控制结构。

由于无法隔离弹体滚转扰动，安装在滚转弹上的两框架平台式导引头光轴将会产生以下3个问题：① 导引头视场内图像旋转，产生控制指令误差；② 光轴上的速率陀螺随光轴滚转，存在视线角速度提取的问题；③ 两框架伺服系统的偏航和俯仰通道受滚转影响，交叉耦合严重。对以上3个关键问题作进一步深入研究，是实现两框架平台式导引头在滚转弹上应用的基础。有关报告显示，美国PAC-3中低空拦截弹已实现在低速滚转的情况下应用两框架雷达导引头[2-3]，但目前国内外暂时没有针对滚转弹上两框架平台式导引头的公开研究。因此，将两框架导引头应用到滚转弹上，对于解决像旋、视线角速度提取以及两通道交叉耦合的问题具有十分重要的实际工程意义。

已有文献中，大多数研究主要针对的是非滚转弹上的两框架平台式导引头，文献[1,4]建立了非滚转弹上的两框架伺服系统动力学模型，文献[5]给出了偏航、俯仰通道的稳定回路动力学模型。在模型基础上，之后的主要研究方向为小滚转角假设下，两通道解耦后的单通道控制问题。针对单通道控制，文献[6]介绍了直接反馈和间接反馈两种稳定方案，文献[7]采用了LQR/LTR控制方法，文献[8]引入了自适应模糊PID控制方法。文献[9]讨论了两种导引头稳定平台的隔离度模型。但是，在不能满足小滚转角假设的情况下，两通道交叉耦合，仅研究单通道控制无法满足精度要求。文献[10]针对倾斜转弯(BTT)导弹出现的大幅度滚转，提出了前馈补偿方案，在250 (°)/s的滚动角速度干扰下，降低了滚动角速度对指令输出的影响。但相对于BTT导弹，滚转弹的滚转角持续增加，滚转角速度维持在 360～1 800 (°)/s 之间，此种情况下该方案无法有效抑制弹体滚转的影响，也未考虑像旋和视线角速度提取的问题。针对以上问题，本文在解决滚转弹上两框架平台式导引头像旋、视线角速度提取和两通道交叉耦合的基础上，设计了符合滚转弹的前馈补偿方案。

本文首先根据导引头工作原理，以及两框架稳定回路模型，结合探测器失调角转换形成视线闭环回路，通过速率陀螺测量值实现视线角速度的提取，建立了滚转弹上两框架导引头的完整模型。接着，在模型建立的基础上推导出导引头控制系统传递函数，分析偏航、俯仰两框架实现解耦独立控制的条件。在模型解耦的基础上，针对弹体滚转对导引头跟踪精度的影响，以及弹体扰动存在时，弹体滚转对隔离度的影响，提出滚转角速度前馈补偿控制方案。最后将导引头模型加入制导仿真回路中，对比有无滚转角速度前馈补偿控制方案时的制导精度。

1 两框架导引头模型建立

1.1 导引头工作原理

两框架速率陀螺式平台导引头组成部分包括探测器、两框架稳定平台以及目标信息处理系统。导引头组成结构如图1所示。

导引头工作原理如图2所示，外回路为视线闭环回路，目标相对导弹在空间的运动经过弹体姿态角和框架角转换投影到探测器坐标系中，根据探测器测量失调角信息，由目标信息处理系统生成控制指令。再由两框架稳定平台控制光轴随框架转动，使光轴指向目标，形成视线跟踪闭环，目的在于保持目标始终位于光轴视场中[11]。内回路为框架伺服系统光轴稳定回路，利用速率陀螺实现光轴转动角速度反馈，形成角速度闭环，目的在于隔离弹体姿态运动对光轴指向的影响[12]。在输出端，目标信息处理系统结合测量光轴转动角速度值、弹体姿态角和框架角，输出视线角速率，为制导律提供所需制导信息[13]。

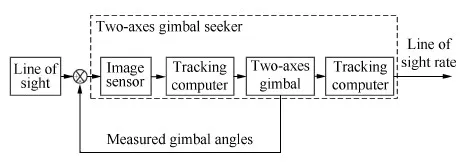
图1 导引头组成结构Fig.1 Structure of seeker

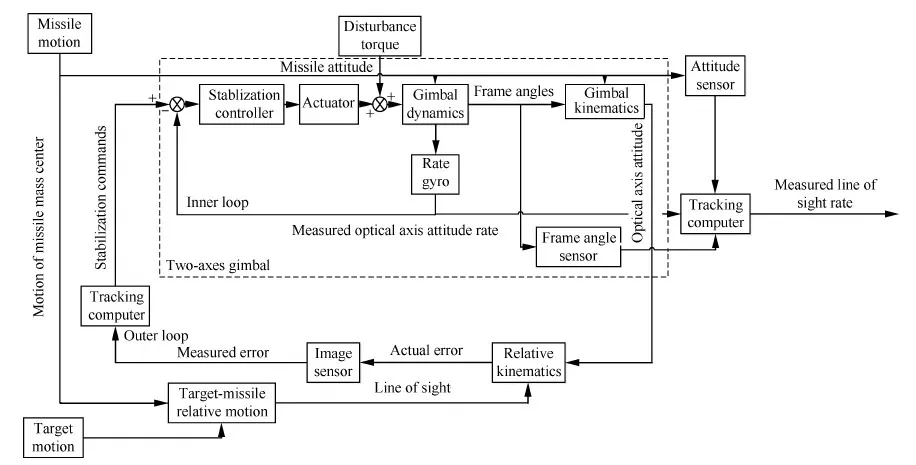
图2 导引头工作原理框图Fig.2 Principle block diagram of seeker

1.2 两框架稳定平台

两框架稳定平台为导引头框架伺服系统，根据输入的控制指令，结合速率陀螺反馈，经过控制器生成指令，通过安装在平台转轴处的直流电机产生控制力拒并带动框架转动，从而控制和稳定光轴在惯性空间的指向[14]。两框架稳定平台的外框为偏航框，安装在弹体基座上；内框为俯仰框，与探测器光轴固连。

为了简化两框架稳定平台模型，给出以下假设：① 速率陀螺为增益为1的理想元件；② 光轴所在两框架稳定平台各转动轴为惯性主轴；③ 外框架三轴转轴的转动惯量通过机械配平。结合电机模型、两框架运动学和动力学，导出偏航框与俯仰框稳定回路框图[15-16]，如图3所示。

ωiy(s)=Gy0(s)Ciy(s)+Gyd(s)Tdo(s)+

Gyb(s)ωby(s)+Gyg(s)ωox(s)

(1a)

ωiz(s)=Gz0(s)Ciz(s)+Gzd(s)Tdi(s)+

Gzb(s)ωoz(s)

(1b)

式中：

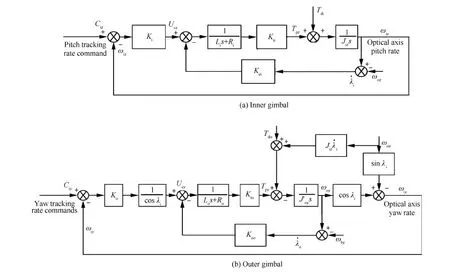
图3 内外框稳定回路框图Fig.3 Stabilized platform block diagram of inner and outer gimbals

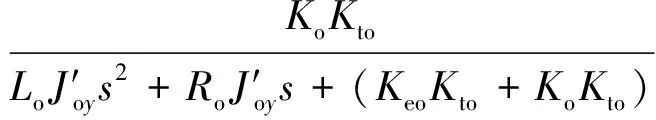
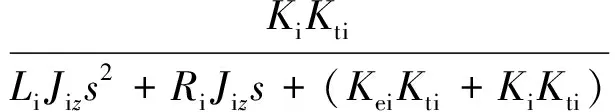
Gyg(s)=

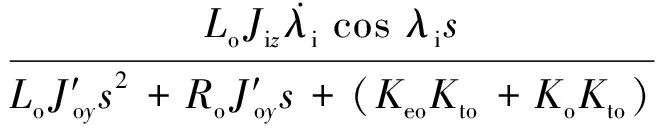
其中，Gy0(s)和Gz0(s)描述了视线角误差产生的控制指令输入对光轴姿态的影响，Gyd(s)和Gzd(s)描述了干扰力矩对光轴姿态的影响，Gyb(s)和Gzb(s)描述了弹体扰动对光轴姿态的影响，Gyg(s)描述了两框架间相互作用对弹体姿态的影响。

由以上导出的传递函数可以看出，两框架稳定平台内框与外框存在耦合。一部分是运动学耦合，产生原因是光轴安装在内框上，其在偏航方向的运动由外框在偏航方向的运动经过内框框架角转换而得；一部分是动力学耦合，外框受到内框运动产生的反作用力矩；一部分是由基座扰动引起的耦合，弹体在偏航方向的姿态扰动通过反电动势回路作用于外框稳定回路，外框在俯仰方向的姿态扰动通过反电动势回路作用于内框稳定回路。在弹体姿态角速度为小量的假设下，以上3部分耦合可近似忽略，这也是以往研究对两通道控制解耦的原因。但对于滚转弹而言，其在滚转方向的角速度不可忽略，所以在研究滚转弹上的两框架稳定平台时，因考虑两框架稳定平台两通道间的耦合。

1.3 导引头完整模型

两框架稳定平台其控制指令由探测器所测失调角结合弹体姿态和框架角给出[17]。实际失调角是光轴指向相对弹目连线在偏航和俯仰方向上的偏差，即视线角跟踪误差。

(2)

(3)

式中：φ为光轴滚转角。根据弹体姿态角和框架角[18]可计算出光轴滚转角在惯性空间的姿态角qy、qz和φ。

一般情况下，偏航、俯仰框控制指令分别由偏航、俯仰通道跟踪环控制器根据失调角给出。假设跟踪环控制器为比例环节：

(4)

式中：Kso和Ksi为跟踪环控制器增益。在系统稳定的情况下，Kso和Ksi决定了视线角跟踪误差的大小，控制器增益越大，跟踪误差越小[8]。

导引过程中，两框架稳定平台保持在对目标的稳定跟踪状态，根据控制器给出的控制指令控制框架转动，并产生相应的光轴转动角速度，具体模型由式(1)给出。在失调角为小量的情况下，即qy≈qy0，qz≈qz0时，光轴指向与弹目线近似重合，可由光轴上安装的速率陀螺测得光轴在惯性空间的转动角速度[19]，提取出光轴在偏航、俯仰方向的角速率变化，近似得到输出视线角速率信息。

(5)

结合探测器失调角转换、两框架稳定平台以及视线角速度提取推导出由输入到输出的导引头系统回路，如图4所示。图4中：ϑ、ψ和γ分别为弹体在俯仰、偏航和滚转方向的姿态角；ωbx、ωby和ωbz分别为弹体在滚转、偏航和俯仰方向的转动角速度。

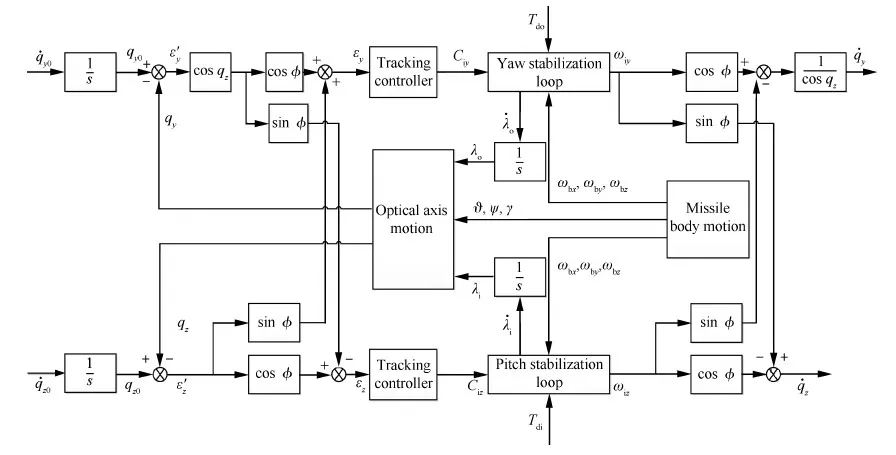
图4 导引头系统框图Fig.4 Block diagram of seeker system

2 导引头输入输出关系与解耦条件

根据图4所示的导引头系统框图，结合跟踪环控制器与实际失调角间的关系：

(6)

以及两框架稳定平台光轴转动角速度与各输入项间的关系：

(7)

(8)

在光轴滚转角φ=0° 的情况下，输入输出关系简化为

(9)

可以看出当光轴滚转角为0°，导弹无滚转时，导引头偏航、俯仰两通道耦合的原因是由两框架稳定平台运动学、动力学以及弹体扰动所造成的。在弹体姿态角速度近似为0° 时两通道近似解耦。

但对滚转弹而言，即使在弹体姿态角速度近似为0 (°)/s的情况下，两通道间也因光轴滚转角不为零而存在耦合。忽略弹体姿态角速度和干扰力矩影响，由式(8)可推出[qy0(s)qz0(s)]T到[qy(s)qz(s)]T的传递函数为

(10)

由式(6)可知，在弹体滚转角不为0° 的情况下，偏航和俯仰两方向的视线角输入输出存在交叉耦合，耦合大小与当前滚转角有关。为了实现两通道独立控制，通过对稳定回路参数和跟踪环控制增益的设置，解耦条件设置为

KsoGy0(s)=KsiGz0(s)

(11)

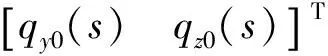
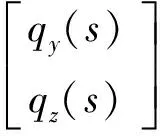
(12)

可以看出，在不考虑弹体姿态角速度和干扰力矩的情况下，通过调节导引头系统稳定回路参数，即可以满足两通道对视线角的输入输出关系解耦。

3 弹体滚转影响和前馈补偿控制

(13)

由式(13)可知，随着光轴滚转角和框架角不断变化，光轴指向与弹体滚转的关系是非线性且时变的，传统的线性控制器难以抑制弹体滚转带给导引头性能的影响。滚转角速度作为弹体扰动输入直接影响了导引头隔离性能，降低了导引头的跟踪精度。对此，本文采取对弹体滚转进行前馈补偿的控制方法[10,20]，在跟踪环控制指令中添加对弹体滚转的前馈补偿项，用以抵消滚转扰动带来的视线角变化。

前馈补偿控制量的大小取决于由弹体滚转角速度带来的探测器失调角变化所产生的控制量变化。由弹体滚转角速度引起的视线角变化可由以式(14)推导得出：

(14)

由视线角变化引起的失调角变化可由式(15)得出：

(15)

由失调角变化所引起的控制指令变化可由式(16)导出：

(16)

取前馈补偿项为控制指令变化相对滚转角速度输入输出关系的增益项，得

(17)

生成新的稳定回路的控制指令为

(18)

4 仿真结果及分析

为了研究弹体滚转的影响，验证前馈增益补偿对弹体滚转的抑制效果，在给定的稳定平台参数下，建立导引头系统框图建立仿真模型[21]。导引头系统稳定平台参数如表1所示。

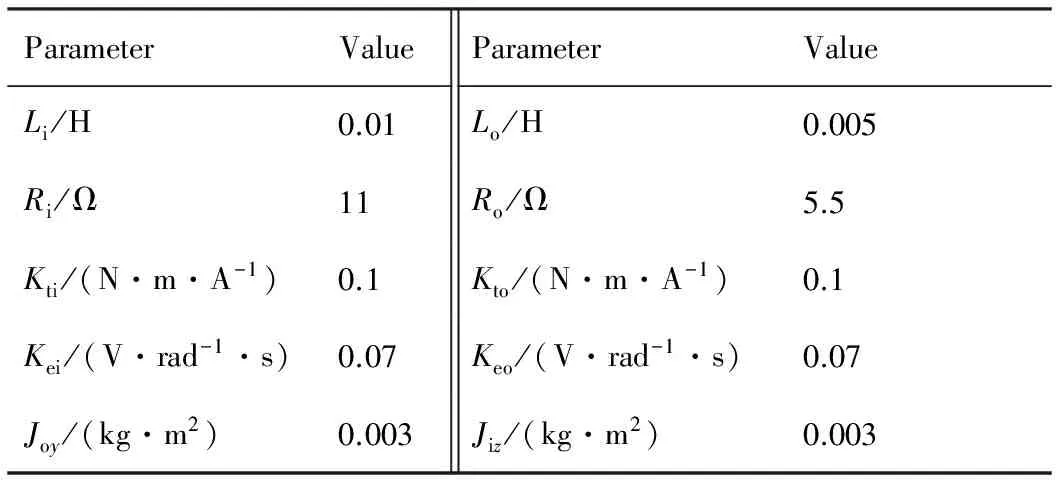
表1 稳定平台参数Table 1 Simulation parameters of gimbal servo system

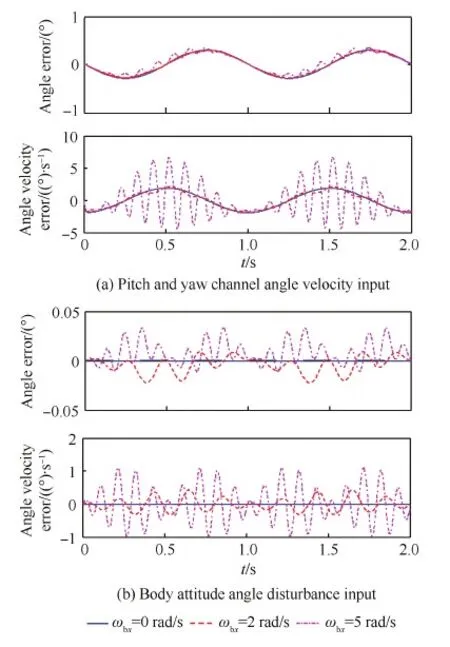
图5 弹体滚转对相应误差的影响Fig.5 Response errors under different roll rates

在仅有弹体扰动输入的情况下，外框框架角λo变化较小，由式(13)可知，由弹体滚转造成跟踪误差的主要因素是Gyg(s)。因此，影响导引头隔离度性能的主要因素是由于在弹体滚转扰动作用下，内外框相互作用对光轴姿态的影响。

在视线角速度输入的情况下，导引头框架角变化范围明显增大，此时影响导引头跟踪误差的主要因素还应包括由Gzb(s)产生的弹体滚转对光轴姿态的影响。由图5可以看出，随着弹体滚转角速度的增大，无论是对视线角速度输入的跟踪，还是对弹体扰动的隔离，导引头性能明显下降，对目标的跟踪精度降低。

为了验证前馈增益补偿对弹体滚转的抑制效果，通过仿真分析对比弹体滚转角速度为 5 rad/s，且导引头系统存在视线角速度输入或弹体扰动输入时，有无弹体滚转前馈补偿对输出视线角和视线角速度误差的影响，具体如图6所示。

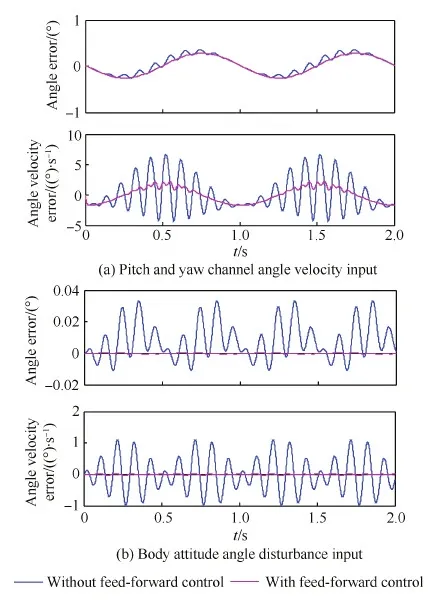
图6 弹体滚转前馈补偿对相应误差的影响Fig.6 Response errors with or without roll missile feed-forward control

由图6中的仿真结果可以看出，无论是视线角速度输入还是弹体扰动输入，弹体滚转角速度的前馈增益补偿都很好地抑制了由弹体滚转引起的视线角和视线速度误差，提高了导引头的跟踪精度。

为了进一步研究导引头系统对导弹制导精度的影响，验证前馈增益补偿对导弹制导系统性能的提高，将导引头系统模型加入导弹仿真大回路中[23]，弹目距离为5 km,初始偏航视线角为-45°，初始俯仰视线角为-30°，导弹速度为500 m/s，目标静止。观察3种情况下导弹飞行轨迹和弹目视线角变化：①弹体无滚转；②弹体以5 rad/s 速度滚转，但无前馈补偿控制；③弹体以5 rad/s速度滚转，有前馈补偿控制。图7和表2为仿真结果对比。

由图7中的仿真结果可以看出，无滚转的导弹在纵向平面内运动，偏航方向视线角变化近似为0°；弹体滚转而无前馈补偿的导弹由于导引头偏航、俯仰通道间的交叉耦合严重，导致导弹的飞行轨迹出现偏航方向的偏差，其偏航视线角出现大范围变化；弹体滚转而有前馈补偿的导弹其飞行轨迹和视线角变化与无滚转的导弹近似，偏航方向运动得到抑制，偏航视线角变化也近似为0°。

表2中给出了情况①、②、③下的脱靶量，同时还对比了目标以60 m/s的速度垂直于初始弹目连线所在纵向平面运动时的脱靶量。

从表2中可以看出，导引头弹体滚转前馈补偿在目标静止和运动两种情况下都降低了脱靶量，有效抑制了弹体滚转对导弹制导精度的影响。

图7 弹体滚转前馈补偿对制导系统的影响Fig.7 Response of guidance system with or without roll missile feed-forward control

表2不同情况下的脱靶量

Table2Missdistancesforfixedandmovingtargetsunderdifferentcases

FixedtargetMissdistance/mMovingtargetMissdistance/mCase①0．11Case①0．09Case②25．12Case②241．39Case③0．17Case③0．22

5 结 论

对于采用两框架平台式导引头的低速滚转弹而言，弹体滚转作为弹体扰动输入，使偏航、俯仰两通道间产生耦合，影响导引头的跟踪精度和隔离度，进一步影响导弹制导精度，产生较大的脱靶量。采用弹体滚转前馈补偿的两框架导引头，其跟踪精度和隔离度性能得到明显改善，导弹制导精度相应提高。在一定程度上，两框架平台式可以代替三框架导引头为低速滚转弹提供制导信息，并取得了较好的制导精度。

[1] RUE A K. Stabilization of precision electrooptical pointing and tracking systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1969, 5(5): 805-819.

[2] HEMAN R, BULTER J. Subsystems for the extended range interceptor (ERINT-1) missile: AIAA-1992-2750[R]. Reston: AIAA, 1992.

[3] O’REILLY P, WALTERS E. Patriot PAC-3 missile program-an affordable integration approach: ADA319957[R]. Dallas: Lockheed Martin Vought Systems Corp., 1996.

[4] RUE A K. Precision stabilization systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(1): 34-42.

[5] EKSTRAND B. Equations of motion for a two-axes gimbal system[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(3): 1083-1091.

[6] KENNEDY P J, KENNEDY R L. Direct versus indirect line of sight (LOS) stabilization[J]. IEEE Transactions on Control Systems Technology, 2003, 11(1): 3-15.

[7] SEONG K J, KANG H G, YEO B Y, et al. The stabilization loop design for a two-axis gimbal system using LQG/LTR controller[C]//Proceedings of 2006 SICE-ICASE International Joint Conference. Piscataway, NJ: IEEE Press, 2006: 755-759.

[8] ABDO M, VALI A R, TOLOEI A R, et al. Modeling control and simulation of two axes gimbal seeker using fuzzy PID controller[C]//Proceedings of 2014 the 22nd Iranian Conference on Electrical Engineering (ICEE). Piscataway, NJ: IEEE Press, 2014: 1342-1347.

[9] 崔莹莹, 夏群力, 祁载康. 导引头稳定平台隔离度模型研究[J]. 弹箭与制导学报, 2006, 26(1): 22-25.

CUI Y Y, XIA Q L, QI Z K. Seeker platform disturbance rejection mathematical model[J]. Journal of Projectiles, Rockets， Missiles and Guidance, 2006, 26(1): 22-25 (in Chinese).

[10] 朱士青, 廖瑛, 雷明兵. 两轴稳定雷达导引头解耦方案研究[J]. 弹箭与制导学报, 2009, 29(5): 6-10.

ZHU S Q, LIAO Y, LEI M B. Study on decoupling scheme of two-axis stabilized radar seeker[J]. Journal of Projectiles, Rockets， Missiles and Guidance, 2009, 29(5): 6-10 (in Chinese).

[11] HILKERT J M. Inertially stabilized platform technology concepts and principles[J]. IEEE Control Systems, 2008, 28(1): 26-46.

[12] MASTEN M K. Inertially stabilized platforms for optical imaging systems[J]. IEEE Control Systems, 2008, 28(1): 47-64.

[13] 姬伟, 李奇. 陀螺稳定平台视轴稳定系统自适应模糊PID控制[J]. 航空学报, 2007, 28(1): 191-195.

JI W, LI Q. Adaptive fuzzy PID control for LOS stabil ization system on gyro stabilized platform[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 191-195 (in Chinese).

[14] DU Y, XIA Q, WANG Z. Effect of seeker disturbance rejection performance on the control system stability[C]//Proceedings of 2010 the 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA). Piscataway, NJ: IEEE Press, 2010: 1032-1035.

[15] LIN C L, HSIAO Y H. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop[J]. IEEE Transactions on Control Systems Technology, 2001, 9(1): 108-121.

[16] 徐娇, 王江, 宋韬, 等. 基于扰动观测器的导引头隔离度抑制方法研究[J]. 兵工学报, 2014, 35(11): 1790-1798.

XU J, WANG J, SONG T, et al. A disturbance observer-based inhibition method for disturbance rejection rate of seeker[J]. Acta Armamentarii， 2014, 35(11): 1790-1798 (in Chinese).

[17] 宋建梅, 孔丽霞, 范健华. 半捷联图像寻的制导系统导引信息构造方法[J]. 兵工学报, 2010, 31(12): 1573-1579.

SONG J M, KONG L X, FAN J H. The guidance information reconstruction of semi-strapdown imaging seeker guidance system[J]. Acta Armamentarii， 2010, 31(12): 1573-1579 (in Chinese).

[18] KHODADADI H, MOTLAGH M R J, GORJI M. Robust control and modeling a 2-DOF inertial stabilized platform[C]//Proceedings of 2011 International Conference on Electrical, Control and Computer Engineering (INECCE). Piscataway, NJ: IEEE Press, 2011: 223-228.

[19] WALDMANN J. Line-of-sight rate estimation and linearizing control of an imaging seeker in a tactical missile guided by proportional navigation[J]. IEEE Transactions on Control Systems Technology, 2002, 10(4): 556-567.

[20] RICHARD D, ROBERT B. Modern control systems[M]. 11th ed. Marquette: Marquette University Faculty, 2011: 34-39.

[21] DEJUN S, DAPENG F, HU L, et al. Bond graph approach to the modeling and simulation of a two-axis pointing and tracking system[C]//Proceedings of 2007 International Conference on Mechatronics and Automation. Piscataway, NJ: IEEE Press, 2007: 2337-2341.

[22] 钱杏芳, 林瑞雄. 导弹飞行力学[M]. 北京： 北京理工大学出版社, 2012: 28-48.

QIAN X F, LIN R X. Missile flight aerodynamics [M]. Beijing: Beijing Institute of Technology Press, 2012: 28-48 (in Chinese).

Feed-forwardcompensationoftwo-axisgimbalseekerinstalledonrollmissile

LIUXiao1,MOBo1,*,LIUFuxiang1,YANXinying2

1.SchoolofAerospaceEngineering,BeijingInstituteofTechnology,Beijing100081,China2.BeijingAerospaceAutomaticControlInstitute,Beijing100854,China

Tosolvethedecouplingcontrolproblemoftwo-axisgimbalseekerinstalledontherollmissile,thestabilizedloopofseekermodelisbuiltbasedonthekinematicsanddynamicsofthetwo-axisgimbal.Inordertogettheclosedlooplineofsight,theinputandoutputundertherollsituationisderived.Thedecouplingconditionisbasedontheassumptionthatthepitchandyawchannelshavethesametransferfunctionbetweenmeasuringdisturbanceangleandopticalaxisrotationspeed.Theeffectofbodyrollrateonthetrackingaccuracyoftheseekerisdiscussedwithlineofsightangleinput,aswellastheeffectofbodyrollrateonthedisturbancerejectionwithbodyattitudedisturbanceinput.Afeedforwardcompensationcontrolmethodisproposedtoreducetheeffectofbodyrollrate.Simulationresultshowsthatthetwo-axisgimbalseekerwithfeed-forwardcompensationcontrolcansatisfythetrackingaccuracyoftherollingmissile.

seeker;servomechanism;bodyrollrate;trackingaccuracy;feed-forwardcontrol

2015-12-02；Revised2015-12-28；Accepted2016-03-11；Publishedonline2016-03-151524

2015-12-02；退修日期2015-12-28；录用日期2016-03-11； < class="emphasis_bold">网络出版时间

时间：2016-03-151524

www.cnki.net/kcms/detail/11.1929.V.20160315.1524.004.html

*

.Tel.：010-68913657E-mailmobo@bit.edu.cn

刘晓， 莫波， 刘福祥， 等． 滚转弹两框架导引头的前馈补偿技术J． 航空学报,2016,37(12):3764-3773.LIUX,MOB,LIUFX,etal.Feed-forwardcompensationoftwo-axisgimbalseekerinstalledonrollmissileJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3764-3773.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0076

V448.13； TJ765.3

A

1000-6893(2016)12-3764-10

刘晓女， 博士研究生。主要研究方向： 飞行器制导与控制。Tel.: 010-68913657E-mail: liuxiaobit@163.com

莫波男， 博士， 研究员， 博士生导师。主要研究方向： 飞行器控制， 控制元件， 检测技术。Tel.: 010-68913657E-mail: mobo@bit.edu.cn

URL：www.cnki.net/kcms/detail/11.1929.V.20160315.1524.004.html

*Correspondingauthor.Tel.：010-68913657E-mailmobo@bit.edu.cn