半捷联位标器稳定跟踪与弹体姿态一体化控制

易科， 陈建， 梁子璇， 任章， 李清东

1.北京航空航天大学 自动化科学与电气工程学院， 北京 100083 2.中国农业大学 工学院， 北京 100083

半捷联位标器稳定跟踪与弹体姿态一体化控制

易科1， 陈建2,*， 梁子璇1， 任章1， 李清东1

1.北京航空航天大学 自动化科学与电气工程学院， 北京 100083 2.中国农业大学 工学院， 北京 100083

半捷联位标器安装在弹体上，由于寄生回路的存在，使得位标器稳定跟踪控制回路和弹体姿态控制回路产生严重耦合，影响了位标器的稳定与跟踪。针对半捷联导引头稳定平台的稳定与跟踪问题，提出了一种半捷联位标器稳定跟踪控制与弹体姿态控制的一体化方法。基于反步控制原理设计了控制律，通过合理选择反馈增益可保证系统的稳定性与动态性能。最后对一体化设计与传统分离设计进行了仿真对比。仿真结果表明：考虑位标器稳定跟踪回路与导弹姿态回路耦合的一体化控制器，不仅能够保证弹体姿态控制系统快速响应，还可以提高位标器的稳定跟踪性能，并降低位标器跟踪不上高速目标的可能性。

半捷联位标器； 稳定跟踪； 姿态控制； 一体化控制； 反步控制

为了满足未来空战的需要，精确制导技术逐渐成为武器系统的核心研究方向。导引头作为精确制导的核心部件，主要作用是为了发现并跟踪目标，实现对目标的自动识别，快速捕获和精确跟踪[1-2]。现在的捷联位标器主要分为全捷联和半捷联两种。全捷联位标器与弹体固连，在目标拦截过程中，弹体的角运动和质心运动以及外部载荷(如风、气流等引起的干扰力矩)会通过各种方式耦合到导引头，严重影响导引头光轴的稳定与跟踪[3-5]。在半捷联稳定方式下，伺服框架无需安装惯性测量元件，减小了导引头框架的体积和质量，降低了成本，通过合理设计平台稳定控制回路，能够实现平台的稳定和对目标的精确跟踪[6]。由于该技术的优势，国外军事强国已将其应用在最新型的空空导弹上，如美国的AIM-9X和欧洲的IRST-T[7-9]。

导引隔离度是评价导引头性能的一个重要指标，用于表征导引头隔离弹体扰动的能力[10-11]。隔离度不仅影响导引头对制导信息的滤波效果，同时还会在制导控制回路中增加一个闭环寄生回路[12-13]。该寄生回路的相位滞后会使得制导控制回路提前失稳，降低导弹制导控制系统的控制性能[14]。

实际上，半捷联导引头的特殊结构使得弹体与半捷联稳定平台框架之间耦合严重。当目标进行大机动或具有较大的横越速度(即目标垂直于视线方向的相对速度)时，导弹需要较大的姿态调整以产生机动来应对目标的相对运动。导弹在调整姿态过程中，如果位标器稳定跟踪控制系统的响应不够及时，可能会导致导引头跟踪不上目标，尤其在制导末端，这种问题变得尤为突出[15]。

国内外研究人员在半捷联位标器稳定跟踪控制方面做了大量的工作。在对半捷联稳定控制系统和弹体姿态控制系统进行设计时，为便于分析考察各分系统的性能，通常将位标器稳定跟踪控制系统、弹体姿态控制系统作为两个独立的部分，割裂开来分别进行研究，采用的是两回路独立设计思想。在这种分离设计思想下，通常都假设半捷联稳定控制系统与弹体姿态控制系统是可解耦的，这样就可以把问题分解为对两个低阶子系统的设计，虽然问题得以简化，但是忽略了系统间耦合的影响。文献[3,16]建立了导引头跟踪框架角误差信号的数学模型，采用数学解析的算法得到框架增量角的求解。文献[17-19]研究了半捷联式天线平台的稳定性，并用角速度补偿法和角位置补偿法两种方法对平台稳定进行了仿真，结果表明，在环境比较恶劣的半捷联稳定平台应用中，角位置补偿法更有优势。

本文针对半捷联稳定平台的稳定与跟踪问题，提出了一种半捷联位标器稳定跟踪控制与弹体姿态控制的一体化方法，给出了一体化控制原理图，该设计考虑了弹体姿态控制回路与位标器稳定跟踪控制回路之间的耦合关系，实现了半捷联位标器的稳定跟踪与弹体姿态的精确控制。

1 位标器稳定跟踪与弹体姿态一体化建模

1.1 坐标系定义及转换关系

为描述方便，定义如下坐标系：

弹体坐标系Sb(ObXbYbZb)：弹体坐标系固连于导弹上，随导弹一起在空间内移动和转动，为动坐标系。坐标原点Ob选取在导弹的质心，ObXb轴沿着导弹的纵轴指向导弹头部；ObYb轴在导弹纵向对称面内，垂直于ObXb指向上方；ObZb轴与ObXb轴和ObYb轴构成右手坐标系。

视线坐标系Ss(OsXsYsZs)：视线坐标系的原点Os选取在探测装置光学系统的光学中心，OsXs轴沿着光学中心与目标的质心连线，指向目标方向；OsYs轴包含在OsXs轴的铅垂面内，垂直于OsXs轴指向上方；OsZs轴与OsXs轴和OsYs轴构成右手直角坐标系。

探测坐标系Sd(OdXdYdZd)：探测坐标系的原点Od选取在探测装置光学系统的光学中心(与Os重合)，OdXd轴沿着探测器的光轴方向，指向探测器的前方；OdYd轴在包含OdXd轴的探测器纵向对称面内，垂直于OdXd轴指向上方；OdZd轴与OdXd轴和OdYd轴构成右手直角坐标系。在半捷联导引头配置方案中，探测坐标系的方向由万向支架的框架方向决定。

如图 1所示，OXoYoZo为外框坐标系；OXiYiZi为内框坐标系，并与探测坐标系OdXdYdZd平行；弹体坐标系与探测坐标系之间的关系由框架方位角λy和框架俯仰角λz两个角确定。从而可得到弹体坐标系到探测坐标系的方向余弦矩阵为

(1)

如图2所示，探测坐标系Sd到视线坐标系Ss之间的关系由失调偏角εy和失调倾角εz确定，

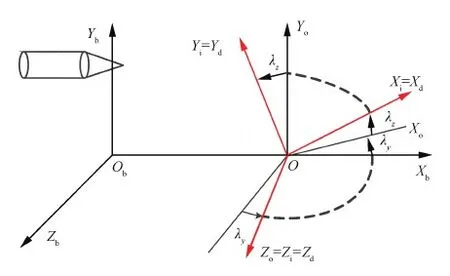
图1 弹体坐标系与探测坐标系之间的关系Fig.1 Relationship between body coordinate system and detection coordinate system

图2 探测坐标系与视线坐标系之间的关系Fig.2 Relationship between detection coordinate system and line-of-sight coordinate system

T为目标在成像平面上的投影。从而可得到探测坐标系到视线坐标系的方向余弦矩阵为

(2)

1.2 弹体姿态动力学模型

半捷联红外成像制导导弹的数学模型与常规导弹的数学模型基本一致。在弹目相对运动中，导弹根据制导指令给出需用过载指令，计算需用过载所需的攻角α、侧滑角β和倾侧角γv可以直接由动力学关系求得。省略中间推导过程，直接给出α、β、γv的微分方程为

(3)

式中：m为导弹质量；g为重力加速度；V为导弹飞行速度；θ和ψv分别为弹道倾角和弹道偏角；L和Y分别为升力和侧向力；ωmx、ωmy和ωmz为导弹姿态角速度在弹体系下的分量。

战术导弹的外形一般都是轴对称的，这时可以认为弹体坐标系就是导弹的惯性主轴系。在此条件下，导弹对弹体坐标系各轴的惯量积为零。可列出姿态角速度微分方程为

(4)

1.3 框架运动学模型

位标器内框安装在外框上，外框架基座与弹体固联。根据刚体运动学原理，导引头光轴的空间运动是基座的运动与框架转动的复合运动，外框的运动是基座运动与外框自身转动的合成，内框的运动是外框耦合运动与内框自身转动共同引起。弹体的姿态运动通过几何约束和摩擦耦合到位标器运动中，中间存在复杂的几何运动关系传递，如图 1所示。

位标器中心的光轴在空间中的运动为

ωd=ωdm+ωds

(5)

式中：

ωd为光轴角速度在探测坐标系中的投影，ωdm为弹体角速度在探测坐标系中的投影，ωds为导引头伺服框架角速度在探测坐标系中的投影。

由式(5)可以看出，光轴在探测坐标系中的角速度是由弹体角速度与框架转动角速度共同组成，弹体的姿态运动会影响光轴的空间指向。跟踪误差作为输入指令，经过导引头稳定跟踪控制器输出框架控制信号，驱动光轴跟踪目标，弹体的运动作为导引头稳定跟踪控制系统的外部干扰。传统的常平架式，可以利用框架上安装的惯性陀螺直接测量框架在惯性空间中的角速度，并反馈至速度稳定闭环系统中以隔离弹体扰动；但是对于半捷联稳定方式，框架上没有安装惯性陀螺，无法直接测量框架在惯性空间中的角速度，需要利用弹体姿态角速度和框架角速度等状态信息，构成速率反馈来实现光轴的稳定。

1.4 角跟踪系统数学模型

导引头空间角关系如图2所示，半捷联角跟踪系统的目的是使得探测坐标系下的光轴OXd跟踪视线坐标系的OXs轴，并保证角跟踪误差最小。对于这两个坐标系，如果已知其中一个坐标系的角速度和两者之间的相对转角，即可准确获得另一个坐标系的角速度。在本系统中，光轴角速度可以通过半捷联稳定平台数字解算得到，光轴与视线之间的失调角可以通过红外成像导引头测量获得。

基于跟踪原理，得到视线坐标系中角跟踪系统基本方程为

(6)

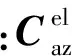
(7)

将式(2)和式(7)代入式(6)中化简，采用小角度近似，可得到三维坐标系下的跟踪角误差微分方程为

(8)

式中：ωy和ωz分别为视线角速率在视线坐标系下的分量，即视线转率；ωdx、ωdy和ωdz为光轴角速度。

由式(5)和式(8)可以看出弹体姿态运动会影响失调角的大小，弹体姿态运动与位标器稳定跟踪运动耦合在一起。

1.5 位标器稳定跟踪与弹体姿态一体化数学模型

导引头输出的制导信号耦合了弹体的姿态运动，并通过制导律、弹体动力学等环节形成了闭合回路。文献[12]分析了寄生回路的形成过程，寄生回路的存在清楚地反应了弹体姿态控制回路和位标器稳定跟踪控制回路之间的耦合关系。因此，半捷联制导系统要实现对目标的稳定跟踪，需要通过半捷联位标器稳定跟踪控制系统和弹体姿态控制系统共同协调控制来实现。

联立弹体姿态动力学模型式(3)和式(4)、框架运动数学模型式(5)和角跟踪系统数学模型式(8)，得到位标器稳定跟踪控制与弹体姿态控制一体化数学模型，将其写成MIMO级联仿射非线性系统，即

(9)

式中：

f1(x1)=

位标器稳定跟踪与弹体姿态控制的问题可以描述为：求解出实现导引头稳定跟踪的框架角速度控制量ωλy和ωλz，实现弹体姿态对参考姿态指令α、β和γv的跟踪，并保证中间状态变量——弹体姿态角速度稳定地控制舵偏δx、δy和δz。

1.6 半捷联导弹制导信息提取

导弹姿态控制系统的指令由制导系统给出，其中制导律所需弹目视线转率可通过制导信息滤波器估计获得。省略中间推导过程，直接给出半捷联导弹的制导信息滤波模型：

(10)

式中：r为导弹与目标间的相对距离；vr为弹目接近速率；atx、aty和atz分别为目标在视线坐标系下的加速度分量；amx、amy和amz分别为导弹在视线坐标系下的加速度分量；qy和qz分别为弹目视线偏角和视线倾角；α0为目标机动加速度时间常数的倒数；wtx、wty和wtz为白噪声。

半捷联导引头的量测信息为两个失调角εy和εz，其量测方程为

(11)

式中：V为量测噪声。

2 一体化控制器

2.1 一体化控制框图

考虑到弹体与导引头之间的相互耦合，以及导引头方位与俯仰运动之间的耦合，需要通过半捷联位标器稳定跟踪控制系统和弹体姿态控制系统共同协调控制来实现导弹对目标的稳定跟踪。基于反步控制理论[20]对级联控制系统式(9)进行一体化控制器设计，如图3所示。

图3中的向量θ和φ分别为弹体姿态角和光轴相对于惯性空间的夹角。制导系统给出的气流角指令αc、βc和γvc，框架角位置测量传感器测得的框架角位置λy和λz，以及导引头测量得到的跟踪角误差εy和εz，通过一体化控制器输出框架角速度控制信号ωλyc和ωλzc，控制光轴指向实时跟踪弹目视线，同时给出弹体姿态角速度的伪控制量ωmxc、ωmyc和ωmzc，送给姿态角速度控制系统输出舵偏角指令δxc、δyc和δzc，控制气动舵实现对姿态角速度的快速跟踪。

2.2 一体化控制器设计

对标称系统式(9)设计控制器之前，先给出以下定理。

图3 基于反步理论的一体化控制器框图Fig.3 Block diagram of integration controller based on backstepping theory

定理1存在正常数αmax<π/2、εmax<π/2和λmax<π/2，当(α,εz,λz)在球B:=

{(α,εz,λz):|α|<αmax,|εz|<εmax,|λz|<λmax}

(12)

内取值时，矩阵g1(x1)均可逆。

证明：由矩阵理论知识可得

det(g1(x1))=

(cos2α-sin2α)secβ(cosλz-εzsinλz)=

(1-2sin2α)secβ(1-εztanλz)cosλz

(13)

式(13)为关于(α,β,εz,λz)的连续函数，由连续函数性质可知，存在正常数αmax<π/2、εmax<π/2 和λmax<π/2使得(α,εz,λz)在球B内时，有

(14)

此时det(g1(x1))≠0，即g1(x1)可逆。

基于定理1，给出如下假设。

假设1在导弹的整个受控飞行过程中，(α,εz,λz)总在式(12)所定义的球B内飞行。

下面介绍带有参数自适应的反步控制器设计过程。

步骤1考虑子系统1：

(15)

定义跟踪误差e1=x1-x1r，设计理想伪控制量x2=x2r和u1，使得e1能渐近收敛到原点。由定理1和假设1可知，在导弹整个受控飞行中g1(x1)可逆。

(16)

步骤2考虑子系统2：

(17)

设计内环控制器u2跟踪伪控制量x2r，定义跟踪误差e2=x2-x2r，使得e2能渐近收敛到原点。显然整个受控飞行中g2(x2)可逆。

(18)

最后得到系统式(9)的反步控制律为

(19)

对g1(x1)求逆可得

(20)

另一方面，控制器式(19)中的反馈增益K1和K2越大，系统的动态响应将会越快，但如果增益选取得过大，那么外界的干扰信号将会被放大，会影响导弹的正常飞行和导引头的稳定跟踪。因此从保证系统稳定工作的角度出发，K1和K2值不宜选得过大。它可以为一个常数，也可以为一个变参数，一般认为，K1和K2中对角元素的值选在5～15之间比较合适。

从式(19)和式(20)中可以看出，设计的中间变量弹体姿态角速度指令ωmxc、ωmyc、ωmzc仅与α、β、γv的跟踪误差有关，输出舵偏指令δxc、δyc和δzc与α、β、γv和伪控制量ωmxc、ωmyc、ωmzc的跟踪误差有关，二者皆与εy和εz无关。一体化设计与分离设计得到的舵偏角指令δxc、δyc和δzc一样。而框架角速度指令ωλyc和ωλzc由α、β、γv和εy、εz的跟踪误差共同决定，框架角速度的控制指令设计耦合了弹体姿态控制。

一体化设计虽然不能改善弹体姿态回路的控制性能，但能改善导引头位标器的稳定与跟踪性能。

2.3 控制系统稳定性证明

定义Lyapunov函数为

(21)

对V1求导，有

(22)

构造复合Lyapunov函数

(23)

对V2求导得

(24)

将控制律式(19)代入式(24)可得

∀e1,e2≠0,K1,K2>0

(25)

设计的控制律为

(26)

能够实现跟踪误差e1和e2渐近收敛到原点。通过选择合适的反馈增益K1和K2，可以保证系统式(9)渐近稳定，并获得期望的动态性能。

3 仿真校验

依据本文的数学模型，在MATLAB/Simulink软件中搭建了半捷联制导导弹的六自由度仿真平台，对所设计的一体化控制器进行了仿真实验。仿真所用气动参数、舵机和伺服电机参数，参考MATLAB自带的Demo:aero_guidance。仿真初始条件如表1所示。表中：ϑ、ψ和γ分别为俯仰角、偏航角和滚转角；θm和ψmv分别为导弹的弹道倾角和弹道偏角；θt和ψtv分别为目标的航迹倾角和航迹偏角。

舵机传递函数为

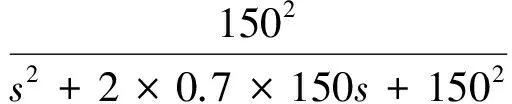
伺服电机传递函数为

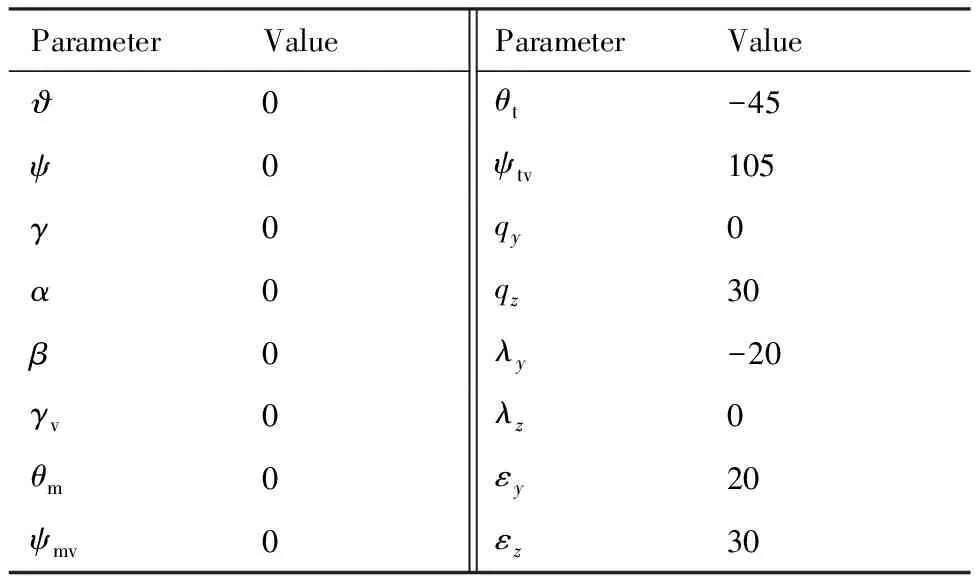
表1 仿真初始条件Table 1 Initial condition for simulation (°)

设导弹初始飞行速度为800 m/s，目标初始飞行速度为400 m/s。由于制导信息的获取不是本文的研究重点，因此假设弹目视线转率能通过制导信息滤波器直接获得。在导弹拦截过程中，选取经典比例导引律作为导弹制导律，导航比为4，导弹的最大可用过载为40g。控制器反馈增益为K1=diag(8,8,8,13,13),K2=diag(13,13,13)。经过与型号研制单位的沟通，得到了误差和噪声的可能上界：导弹的攻角、侧滑角与倾侧角的导航解算误差为0.5°，伺服框架角测量噪声为0.5°，导引头失调角测量噪声为0.5°。

下面将对两种情况进行仿真分析：① 某一相对初始态势下分离设计与一体化设计的控制效果对比；② 不同相对初始态势下的分离设计与一体化设计的控制效果对比。各仿真结果中，RC表示传统分离设计的速率补偿方法；ISAC为一体化设计方法。

3.1 情况 1

弹目初始距离为3 000 m，假设拦截过程中，目标采用常值机动方式以规避导弹的攻击，法向和侧向机动过载均为-8g。其他仿真初始条件如表1所示。

仿真终止条件为弹目相对距离r≤20 m。分别对一体化设计和分离设计的位标器稳定跟踪与弹体姿态控制进行仿真分析，仿真结果如图4所示。

图4(a)与图4(b)为一体化设计与分离设计的弹体姿态跟踪曲线对比。由仿真曲线可以看出弹体姿态回路的动态响应曲线完全重合，α和β的跟踪曲线响应很快，在0.6 s内收敛，跟踪误差趋近于零。图4(c)与图4(d)为一体化设计与分离设计的舵偏角，可以看到两种设计方法得到的舵偏角δy和δz一样，这是由于一体化控制器得到的舵偏角指令δxc、δyc和δzc仅与α、β、γv和伪控制量ωmxc、ωmyc、ωmzc的跟踪误差相关，而与失调角εy和εz无关，这同前文分析得到的结论一致，即一体化设计不改善弹体姿态回路的控制性能。仿真结果表明一体化设计与分离设计的控制器一样，对弹体姿态的跟踪误差较小，都具有满意的动态性能。

图4(e)与图 4(f)为一体化设计与分离设计的导引头失调角曲线对比。采用分离设计的失调角跟踪误差较大，而采用一体化设计的失调角在0.45 s内收敛趋近于零。采用一体化设计的失调角控制曲线与分离设计的相比，收敛速度更快、跟踪误差更小。这主要是由于分离设计未考虑位标器与弹体姿态之间的耦合，各子系统之间的协调性较差，导致设计的控制律保守性更大，系统的控制精度较低；而一体化设计考虑了两个子系统之间动态特性的相互影响，降低了系统设计的保守性。

同时从图4(c)、图4(d)、图4(g)与图4(h)中可以看出，由于反馈信息中存在测量噪声，反馈增益会放大该噪声，使得两种方法的控制输出(舵偏角与框架角速率)存在抖动，不过抖动的幅值很小，工程上可以接受。但是，如果将测量噪声增大为1° 和1.5°，可以发现执行机构发生了剧烈抖动(如图5所示)，这种抖动不利于执行机构的工作，可能会损坏执行机构，进而可能会影响系统的稳定性。综上，过大的反馈增益会放大测量噪声；而反馈增益过小，系统的动态性能较差。因此，在工程设计中，需根据系统的动态指标和传感器测量噪声的可能上界，合理选取反馈增益K1和K2，以保证系统的控制性能。

3.2 情况2

当弹目初始相对态势不佳时，导弹需要以较大的机动去打击目标，若位标器控制性能不佳，会导致导引头失调角较大。现假定导弹与目标只在纵向平面发生相对运动，弹目初始相对距离为1 500 m，初始时刻导弹水平向前飞行，目标做匀速运动，分别以不同航迹倾角(30°、50°、70°、90°)从导弹正前方飞过，导引头俯仰方向初始失调角为30°。

仿真时间为2 s，限于篇幅，仅给出仿真中失调角这一关键参数的变化曲线。图6(a)为不同航迹角下传统速率补偿的导引头跟踪效果，图6(b)为不同航迹角下一体化控制的导引头跟踪效果。

从图6的仿真结果中可以看出，随着目标垂直于视线方向的相对速度(即横越速度)增大，采用传统分离设计的导引头失调角控制效果逐渐变差。特别的，当目标以垂直于导弹正上方飞过时，导引头失调角已经开始发散，这可能会导致目标逃离导引头的视场，无法被成功拦截；而采用一体化设计的导引头失调角控制效果明显优于前者，即使在极端情况下仍能保证失调角很小，保证目标位于导引头光轴中心。图6(b)中出现的几处小超调，是由于导弹需用过载离开饱和区域后的攻角指令变化所致。

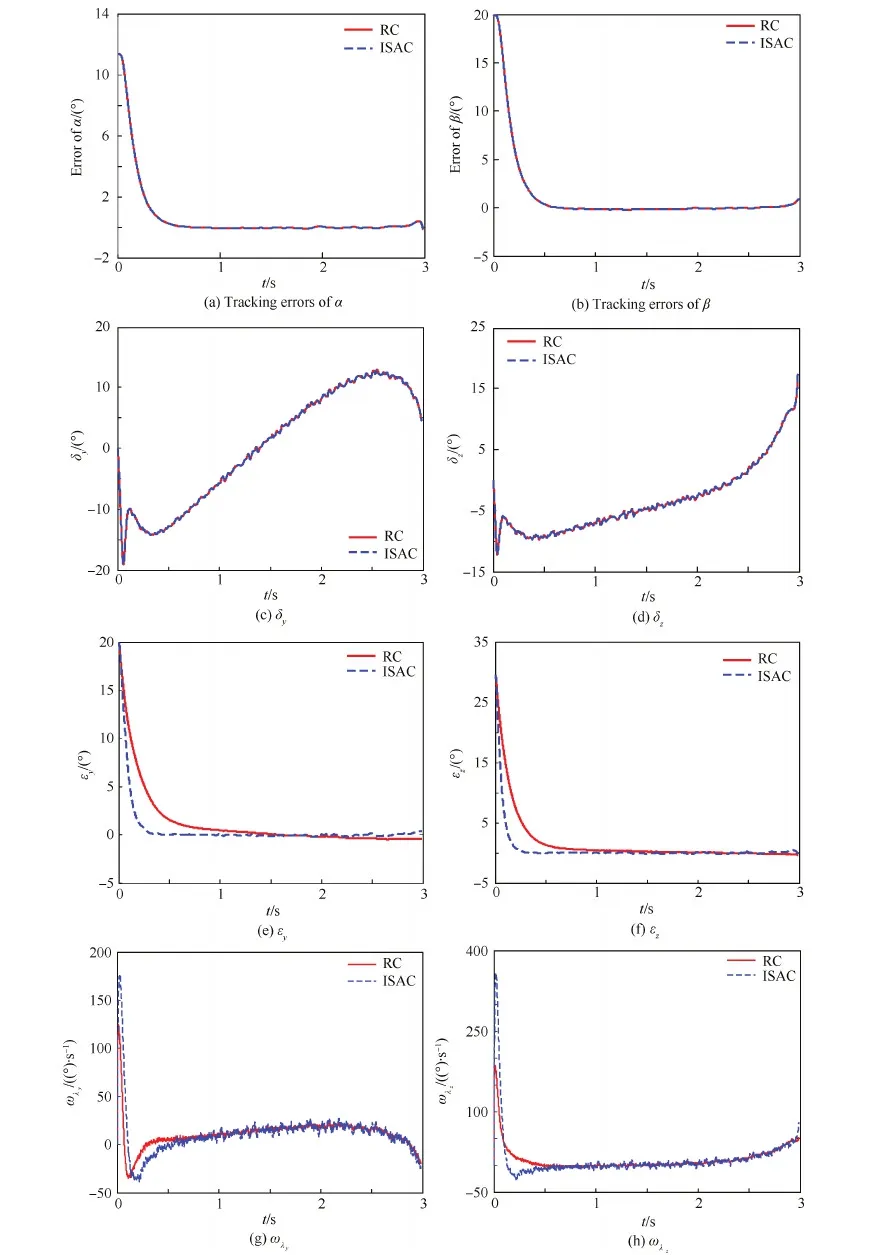
图4 速率补偿与一体化设计的控制效果对比Fig.4 Comparison of control effects under rate compensation and integration design

图5 不同噪声下的框架角速率ωλz变化曲线Fig.5 Variation curves of frame angular rate ωλz with different noises

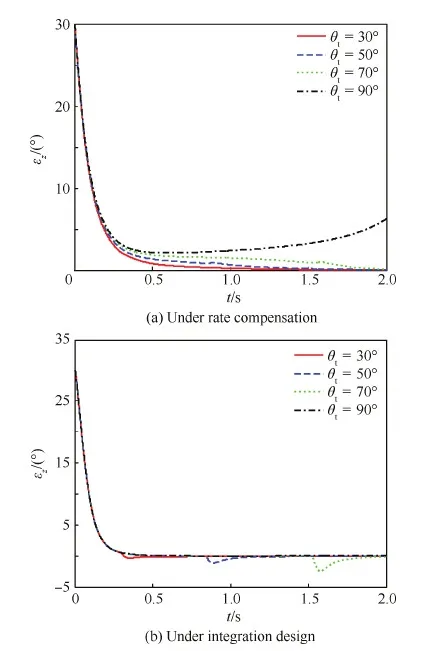
图6 不同条件下的两种方法跟踪效果对比Fig.6 Comparison of tracking effects under two methods with different conditions

4 结 论

1) 本文建立了半捷联制导导弹的弹体姿态运动与位标器稳定跟踪一体化模型，解释了位标器稳定跟踪控制回路和弹体姿态控制回路之间的耦合关系。

2) 根据一体化模型，建立了基于反步控制的一体化控制律，该控制律能够保证弹体姿态运动与位标器稳定跟踪一体化模型的收敛性，解决了控制回路之间的耦合问题。

3) 仿真结果表明，设计的一体化控制器具有较好的控制性能，不仅仍然能保证导弹对姿态指令的快速跟踪，还能提高位标器的稳定跟踪性能，防止导引头跟踪不上具有大横越速度的目标，确保目标位于导引头光轴的中心附近，具有较小的失调角。这对于半捷联导弹控制系统的工程设计具有重要的应用价值。

[1] 李保平. 战术导弹导引头技术[J]. 弹箭与制导学报, 2002, 22(1): 1-5.

LI B P. Seeker technique of tactical missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2002, 22(1): 1-5 (in Chinese).

[2] 周瑞青. 捷联导引头稳定与跟踪技术[M]. 北京： 国防工业出版社, 2010: 1-9.

ZHOU R Q. Stabilization and tracking technique for strapdown platform[M]. Beijing: National Defense Industry Press, 2010: 1-9 (in Chinese).

[3] LIN C L, HSIAO Y H. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop[J]. IEEE Transactions on Control Systems Technology, 2001, 9(1): 108-121.

[4] 朱华征, 范大鹏, 马东玺, 等. 导引头伺服系统隔离度与测试[J]. 光学精密工程, 2009, 17(8): 1993-1998.

ZHU H Z, FAN D P, MA D X, et al. Disturbance isolation index of seeker servo system and its test[J]. Optics and Precision Engineering, 2009, 17(8): 1993-1998 (in Chinese).

[5] 吴晔, 朱晓峰, 陈峻山. 导引头二轴稳定平台的轴角关系和简化[J]. 制导与引信, 2012, 33(1): 1-5.

WU Y, ZHU X F, CHEN J S. Axis-angle relationships and their simplifications in two-axis stabilied platform of radar seeker[J]. Guidance & Fuze, 2012, 33(1): 1-5 (in Chinese).

[6] RUDIN R T. Strapdown stabilization for imaging seekers[C]//Proceedings of the 2nd Annual AIAA SDIO Interceptor Technology Conference. Reston: AIAA, 1993: 1-10.

[7] 任淼, 王秀萍. 2011年国外空空导弹发展综述[J]. 航空兵器, 2012 (3): 3-7.

REN M, WANG X P. Overview on foreign air-to-air missiles development in 2011[J]. Aero Weaponry, 2012 (3): 3-7 (in Chinese).

[8] 穆学桢, 周树平, 赵桂瑾. AIM-9X空空导弹位标器新技术分析和评价[J]. 红外与激光工程, 2006, 35(4): 392-394.

MU X Z, ZHOU S P, ZHAO G J.Analysis and evalution of new approach of AIM-9X AAM seeker[J] . Infrared and Laser Engineering, 2006, 35(4): 392-394 (in Chinese).

[9] 樊会涛. 第五代空空导弹的特点及关键技术[J]. 航空科学技术, 2011(3): 1-5.

FAN H T. Characteristics and key technologies of the fifth generation of air to air missiles[J]. Aeronautical Science & Technology, 2011(3): 1-5 (in Chinese).

[10] 赵超. 导引头稳定系统隔离度研究[J]. 电光与控制, 2008, 15(7): 78-82.

ZHAO C. Study on disturbance rejection rate of a seeker servo system[J]. Electronics Optics &Control, 2008, 15(7): 78-82 (in Chinese).

[11] 李富贵, 夏群利, 崔晓曦, 等. 导引头隔离度寄生回路对视线角速度提取的影响[J]. 宇航学报, 2013, 34(8): 1072-1077.

LI F G, XIA Q L, CUI X X, et al. Effect of seeker disturbance rejection rate parasitic loop on line of sight rate extraction[J]. Journal of Astronautics, 2013, 34(8): 1072-1077 (in Chinese).

[12] 杜运理, 夏群利, 祁载康. 导引头隔离度相位滞后对寄生回路稳定性影响研究[J]. 兵工学报, 2011, 32(1): 28-32.

DU Y L, XIA Q L, QI Z K. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop[J]. Acta Armamentarii, 2011, 32(1): 28-32 (in Chinese).

[13] 李富贵, 夏群利, 祁载康. 导引头隔离度寄生回路对最优制导律性能的影响[J]. 航空学报, 2013, 34(12): 2658-2667.

LI F G, XIA Q L, QI Z K. Effect of seeker disturbance rejection rate parasitic loop on performance of optimal guidance law[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2658-2667 (in Chinese).

[14] 徐平, 王伟, 林德福. 导引头隔离度对末制导炮弹制导控制的影响[J]. 弹道学报, 2012, 24(1): 17-21.

XU P, WANG W, LIN D F. Effect of seeker isolation on guidance and control of terminal guided projectile[J]. Journal of Ballistics, 2012, 24(1): 17-21 (in Chinese).

[15] 姚郁, 章国江. 捷联成像制导系统的若干问题探讨[J]. 红外与激光工程, 2006, 35(1): 1-6.

YAO Y, ZHANG G J. Discussion on strapdown imaging guidance system[J]. Infrared and Laser Engineering, 2006, 35(1): 1-6 (in Chinese).

[16] 王志伟， 祁载康， 王江. 滚-仰式导引头跟踪原理[J]. 红外与激光工程, 2008, 37(2): 274-277.

WANG Z W, QI Z K, WANG J. Tracking principle for roll-pitch seeker[J]. Infrared and Laser Engineering, 2008， 37(2): 274-277 (in Chinese).

[17] 赵超. 基于角速度补偿的捷联天线稳定系统设计[J]. 电光与控制, 2010, 17(9): 60-64.

ZHAO C. Design of an angular-rate compensation based strapdown antenna stabilization system[J]. Electronics Optics & Control, 2010, 17(9): 60-64 (in Chinese).

[18] KENNEDY P J, KENNEDY R L. Direct versus indirect line of sight (LOS) stabilization[J]. IEEE Transactions on Control Systems Technology, 2003, 11(1): 3-15.

[19] 周瑞青, 吕善伟, 刘新华. 弹载捷联式天线平台两种稳定实现方法的比较[J]. 系统工程与电子技术, 2005, 27(8): 1397-1400.

ZHOU R Q, LYU S W, LIU X H. Comparison of two stabilization methods for airborne strapdown antenna platform[J]. Systems Engineering and Electronics, 2005, 27(8): 1397-1400 (in Chinese).

[20] LIAN B, BANG H, HURTADO J E. Adaptive backstepping control based autopilot design for reentry vehicle[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2004: 1-10.

[21] 李菁菁, 任章, 宋剑爽. 高超声速再入滑翔飞行器的模糊变结构控制[J]. 上海交通大学学报, 2011, 45(2): 295-300.

LI J J, REN Z, SONG J S. Fuzzy sliding mode control for hypersonic re-entry vehicles[J]. Journal of Shanghai Jiaotong University, 2011, 45(2): 295-300 (in Chinese).

Integrationcontrolofsemi-strapdowncoordinatorstabletrackingandmissilebodyattitude

YIKe1,CHENJian2,*,LIANGZixuan1,RENZhang1,LIQingdong1

1.SchoolofAutomationScienceandElectricalEngineering,BeihangUniversity,Beijing100083,China2.CollegeofEngineering,ChinaAgriculturalUniversity,Beijing100083,China

Thesemi-strapdowncoordinatorislocatedonthemissilebody.Becauseoftheexistenceoftheparasiticloop,thecontrolloopforstabletrackingofthesemi-strapdowncoordinatorisstronglycoupledwiththecontrolloopofthemissilebodyattitude.Asaresult,thestabilityandtrackingperformanceofthecoordinatorareseverelyaffected.Inordertosolvethisproblem,anintegrationcontrolmethodisproposed.Controllawisdesignedbasedonthebacksteppingtheory.Stabilityanddynamicperformanceofthesystemcanbeensuredbychoosinganappropriatefeedbackgain.Theintegratedcontrolsystemisverifiedbysimulations.Resultsshowthattheintegrationcontroller,whichconsidersthecouplingbetweenthecoordinatorstabletrackingloopandthemissileattitudeloop,cannotonlyensurethedynamicperformanceofthemissileattitudecontrolsystem,butalsoimprovethestabletrackingperformanceofthecoordinatorandpreventthehigh-speedtargetfromescapingfromthefieldofviewofthemissileseeker.

semi-strapdowncoordinator;stabletracking;attitudecontrol;integrationcontrol;backsteppingcontrol

2016-01-15；Revised2016-02-18；Accepted2016-04-26；Publishedonline2016-04-290832

URL：www.cnki.net/kcms/detail/11.1929.V.20160429.0832.002.html

s：NationalNaturalScienceFoundationofChina(61333011);AVICInnovationFunds(cxy2012BH01)

2016-01-15；退修日期2016-02-18；录用日期2016-04-26； < class="emphasis_bold">网络出版时间

时间：2016-04-290832

www.cnki.net/kcms/detail/11.1929.V.20160429.0832.002.html

国家自然科学基金 (61333011)； 中航工业创新基金 (cxy2012BH01)

*

.Tel.：010-82314573E-mailchenjian@buaa.edu.cn；jchen@cau.edu.cn

易科， 陈建， 梁子璇， 等． 半捷联位标器稳定跟踪与弹体姿态一体化控制J． 航空学报,2016,37(12):3752-3763.YIK,CHENJ,LIANGZX,etal.Integrationcontrolofsemi-strapdowncoordinatorstabletrackingandmissilebodyattitudeJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3752-3763.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0128

V448.133

A

1000-6893(2016)12-3752-12

易科男， 博士研究生。主要研究方向： 制导信息滤波、 飞行器制导与控制、一体化设计。E-mail: yikebuaa@buaa.edu.cn

陈建男， 博士， 副教授。主要研究方向： 飞行器导航、 制导与控制、 一体化设计、 无人机控制。Tel.: 010-82314573E-mail: chenjian@buaa.edu.cn；jchen@cau.edu.cn

梁子璇男， 博士。主要研究方向： 飞行器轨迹规划与制导技术。E-mail: aliang@buaa.edu.cn

任章男， 博士， 教授， 博士生导师。主要研究方向： 飞行器导航、 制导与控制、 精确制导技术、 控制系统故障检测与诊断、 系统仿真与仿真系统集成。E-mail: renzhang@buaa.edu.cn

李清东男， 博士， 讲师。主要研究方向： 飞行器导航、 制导与控制， 故障检测与诊断、 容错控制、 人工智能。E-mail: muziqingdong@126.com

*Correspondingauthor.Tel.：010-82314573E-mailchenjian@buaa.edu.cn;jchen@cau.edu.cn