基于弹簧质量模型的复合材料螺接修理载荷传递计算方法

谢宗蕻， 李想， 杨淋雅， 吴师

1.西北工业大学 航天学院， 西安 710072 2.中国航空工业集团公司 第一飞机设计研究院， 西安 710089

基于弹簧质量模型的复合材料螺接修理载荷传递计算方法

谢宗蕻1,*， 李想1， 杨淋雅2， 吴师1

1.西北工业大学 航天学院， 西安 710072 2.中国航空工业集团公司 第一飞机设计研究院， 西安 710089

复合材料螺接修理具有操作简便，对连接件表面处理的要求不高，施工快速、性能可靠等优点，在复合材料的临时修理、尤其是战伤修理中应用较为广泛。然而其修理设计过程较为复杂，难以满足工程快速定参的需要。在螺接接头弹簧质量模型的基础上，针对蒙皮和补片等宽的情况，提出了一种复合材料螺接修理结构载荷传递比例计算方法。通过引入载荷按刚度分配的原则对模型进行修正，将模型进一步推广到蒙皮宽度大于补片宽度的情况。然后讨论了模型中不同弹簧刚度的计算方法。给出了采用细观力学方法以及均匀化方法等计算含损伤蒙皮等效刚度的计算方法，推导得到了规则排列多列螺栓连接中各排螺栓等效刚度的计算方法，并证明该刚度满足叠加原理。最后，以含圆形损伤孔的复合材料蒙皮板的螺接修理问题为例，对模型进行了考核，并与有限元法(FEM)预测结果进行了对比。结果表明：模型预测结果与有限元结果吻合较好，预测误差最大为7.7%。采用该模型可以高效、准确地实现复合材料螺接修理的分析设计。

复合材料； 螺接修理； 载荷传递； 钉载分配； 弹簧质量模型

随着飞机结构上复合材料的大量采用及对飞机寿命要求的不断提高，复合材料受损结构的修理问题正成为目前航空领域亟待解决的技术问题。出于性能可靠以及操作简单等考虑，工程中通常采用复合材料螺栓或者铆钉将补片固定到损伤结构上，这种修理方法称为螺接修理。螺接修理传递到补片上的载荷比例对损伤结构的孔边应力、修理效率以及破坏模式等有重要影响，国内外学者对其开展了大量研究。

目前，复合材料螺接修理的研究方法主要包括试验方法[1]、有限元法[1-5]、复势函数法[6-7]和边界元法[8]等。

聂恒昌等[1]对含圆形损伤孔的复合材料层合板不同机械修理方案进行了试验研究和理论分析。研究发现，修理后的复合材料层合板，其强度恢复率达到55%～60%，应力集中的部位主要在修理区域外最外侧的钉孔旁，最终破坏模式为母板沿修理区域最外侧一排钉孔断裂。杜奎等[2]采用有限元法(FEM)，建立了含圆孔复合材料机械连接修理模型，研究了螺钉数目、行/列间距等参数对圆孔应力集中系数的影响。赵美英等[3]采用有限元法，研究了补片直径、厚度、铺层、修理方式等参数对复合材料层合板穿透损伤修补效率的影响。Bortman和Szabo[4]则采用p型有限元对剪切载荷条件下的复合材料螺接修理接头进行了研究。Shi等[5]采用二维有限元技术对双轴加载情况下，不同补片对复合材料螺接修理的孔边应变的影响进行了研究。Barut等[6]基于复势函数法和变分方法，建立了一种分析螺接接头应力分布的二维半解析方法。Kradinov等[7]采用势能变分法研究了开孔复合材料层合板螺接修理的有效性。Zhang[8]采用边界元方法对螺接修理接头进行了分析。

尽管复合材料螺接修理的研究已取得了一些成果，然而对复合材料螺接修理中的关键参数，即传递到补片上的载荷比例，目前并无简便有效的计算方法，这在一定程度上限制了螺接修理的工程化应用。

螺接修理接头作为一种特殊的螺接接头结构，可沿用常规螺接接头的分析方法。在众多螺接接头的分析模型中，弹簧质量模型由于具有结构形式简单、精度高、能综合考虑不同参数对载荷传递规律的影响等特点，在工程领域中得到了广泛的应用。

1946年，Tate和Rosenfeld[9]开拓性地提出了弹簧质量模型，并成功用于各向同性材料多钉双剪接头的钉载分配分析，奠定了弹簧质量模型的基础。Nelson等[10]将弹簧质量模型推广应用到各向异性材料和单剪接头的分析中，使得该方法在工程领域得到了广泛的关注。McCarthy等[11-12]将弹簧质量模型分别推广到考虑钉孔间隙和拧紧力矩的情况。谢宗蕻等[13]将弹簧质量模型推广应用于考虑钉孔间隙的多钉连接钉载分配的优化中。

目前该方法主要用于单列多钉连接接头钉载分配的分析，模型并未考虑搭接板的缺陷如开孔损伤对连接板刚度的影响，因而并不能直接用于螺接修理接头的分析。本文对传统的弹簧质量模型进行改进，以规则分布的多排钉螺接修理接头为对象，通过引入开孔板刚度、等效螺栓刚度、接头刚度等参数，建立一种计算复合材料螺接修理载荷传递的解析方法。然后以拉伸载荷作用下含圆形损伤孔的复合材料蒙皮的单面修理和双面修理为例，对模型进行考核。

1 螺接修理载荷传递估算

图1所示为从受损飞行器结构中取出的典型复合材料螺接修理接头分离体，包括维修补片和含损伤蒙皮。蒙皮长为LP，宽为wP，厚为tP，补片长度为LR，宽为wR，厚为tR，损伤区为圆形损伤，直径为D，半径记为R。螺钉规则排列，螺栓布局关于y轴对称，排距记为pi(i=1,2,…,n,其中，p1为第1排螺栓与y轴之间的距离)，列距为S，端距为e，边距为Sw。修理方式为单面修理或者双面修理，载荷形式为单向拉伸载荷，载荷大小为F。本研究将采用弹簧质量模型推导该螺接修理结构传递到补片上的载荷比例的控制方程。

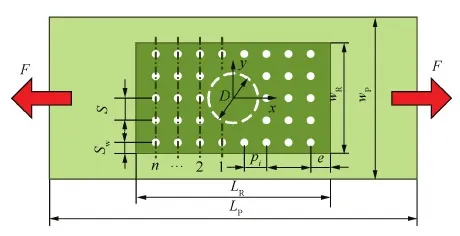
图1 复合材料螺接修理接头几何尺寸Fig.1 Geometries of bolted repair of composite joint

1.1 蒙皮与补片等宽的情况

弹簧质量模型用于传统的螺接接头分析时，一般令连接板的宽度相同，因此，本文推导时，也首先考虑连接板(蒙皮和维修补片)等宽的情况，即令wP=wR。另外引入如下基本假设：① 螺栓排列方式为类似图1所示的规则排列形式；② 螺栓位于孔的中心位置；③ 螺栓预紧力很小，忽略垫圈、螺栓以及连接板之间的摩擦效应(该假设适用于螺栓手动拧紧的机械连接接头)；④ 多排螺接修理中，每排中各螺栓沿载荷方向位移相同；⑤ 损伤区域为规则形状的损伤(圆形损伤、椭圆形损伤以及长圆孔形损伤)；⑥ 钉孔之间配合无间隙。

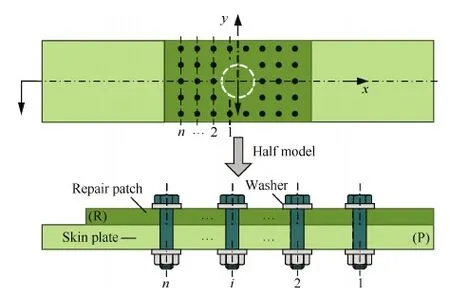
图2 多排紧固件螺接修理接头截面视图Fig.2 Section view of multi-column bolted repair joint

(1)

同理对其他质量块进行类似的受力分析，可以得到质量块的位移与外载荷之间的线性方程组为

KX=V

(2)

式中：K为刚度矩阵；X为质量块位移向量；V为载荷向量。

图3 多排紧固件螺接修理接头弹簧质量模型Fig.3 Spring-mass model for multi-column bolted repair joint

K=

(3)

(4)

(5)

各排螺栓的载荷为

(6)

钉载比例为

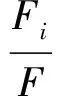
(7)

传递到补片上的载荷比例为

(8)

特别地，对于紧固件排数为1的情况，如图4所示，传递到补片上的载荷等于该排所有紧固件所传递的载荷之和。求解式(2)～式(5)，可得质量块1、2的位移，即

(9)

将式(9)代入式(6)和式(7)可得到螺栓的钉载比例，即传递到补片上的载荷比例为

(10)

图4 单排螺钉修理Fig.4 Single-column bolted repair

η=f1+f2

(11)

(12)

式中：η1和η2分别为第1排和第2排螺栓的钉载比例。

1.2 蒙皮宽度大于补片宽度的情况

当蒙皮宽度大于补片宽度时，需对式(8)得到的载荷比例进行修正。本文拟采用载荷按刚度分配的原则对该情况进行研究。

将分离的修理结构分为修理区和未损伤区两部分，如图5所示。记两部分的刚度分别为KRR和KUR，承担的载荷分别为FRR和FUR，并且

F=FRR+FUR

(13)

修理结构的刚度为

KRR+UR=KRR+KUR

(14)

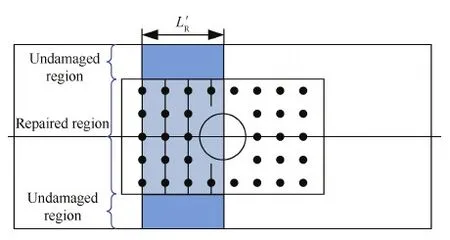
图5 修理结构未损伤区和修理区 Fig.5 Undamaged and repaired regions in repaired structure

根据载荷按刚度分配的原则，有

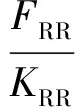
(15)

因此，当蒙皮宽度大于补片宽度时，传递到补片上的载荷可按式(16)计算。

(16)

式中：ηRR+UR为考虑非修理区后传递到补片上的载荷比例；ηRR为只考虑图5所示修理区时计算的传递到补片上的载荷传递比例，可根据式(2)～式(7)计算。理论上，载荷比例ηRR的计算对应的载荷条件为FRR，但由于模型中不考虑间隙及摩擦等非线性因素的影响，实际上，可在任意大小载荷下进行计算。

修理区的刚度KRR可通过求解式(2)～式(5)并根据式(17)确定。

KRR=FRR/x2n-1

(17)

对非修理区，其刚度为光滑层压板的刚度，即

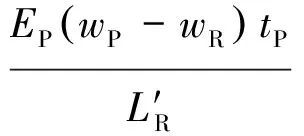
(18)

2 弹簧刚度计算

2.1 蒙皮和补片刚度

本节分别计算蒙皮以及补片的刚度。以1号螺栓和y轴之间的蒙皮为例，若损伤区较小，可忽略损伤孔对蒙皮刚度的影响，此时蒙皮可视为光滑层压板(Unnotched)，其刚度为

(19)

式中：EP为蒙皮沿加载方向的弹性模量。

若损伤区尺寸较大，需要考虑损伤孔对蒙皮刚度的影响时，蒙皮刚度可基于复合材料细观力学(Micromechanics)横向等效刚度的计算方法计算。刚度等效基于如下假设：蒙皮上与载荷方向垂直的平面，变形后依然保持为一平面。若基于细观力学计算蒙皮刚度，则有

(20)

如图6[14]所示，将蒙皮视为开孔板，截面积可以写为

A(x)=tPw(x)

(21)

蒙皮宽度w(x)可以表示为

(22)

将式(21)和式(22)代入式(20)，采用变量代换令x=Rsinθ，0≤θ≤π/2，可对式(20)进行显式积分，积分后可得

(23)

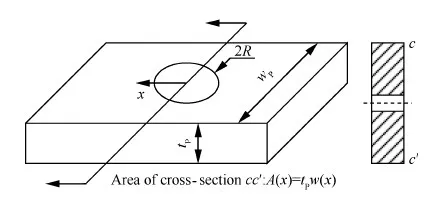
图6 开孔板横截面[14]Fig.6 Cross-section of plate with an open-hole[14]

同理，当损伤区域为其他的规则形状时，也可采用上述的细观力学方法推导损伤区的蒙皮刚度。例如，对于含椭圆形和长圆孔形两种损伤的蒙皮板，也可参考上面的方法推导蒙皮的等效刚度。参考图7椭圆形和长圆孔形两种典型损伤，蒙皮宽度的表达式分别如式(24)和式(25)所示。

对椭圆形损伤，有

(24)

对长圆孔形损伤，有

(25)

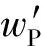
将式(24)和式(25)分别代入式(20)积分，可得两种损伤形式蒙皮的等效刚度如式(26)和式(27)所示。

对椭圆形损伤，有

(26)

对长圆孔形损伤，有

图7 椭圆形和长圆孔形两种典型损伤几何形状Fig.7 Two typical damage modes of ellipse and oblong ellipse and their geometries

(27)

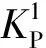
比较以上几种蒙皮刚度的等效方法，可以看到，等效过程中的约束逐渐减弱，因此，采用以上3种方法计算的损伤区蒙皮等效刚度满足光滑层压板方法>细观力学方法>均匀化方法。实际中，损伤区的尺寸和蒙皮的面内尺寸相比，往往不可忽略，因此推荐采用细观力学和均匀化方法计算蒙皮刚度。

对于不包含损伤区的其他排螺栓之间的蒙皮段，可视为光滑层压板，等效刚度参考式(19)计算。

需要注意的是，对蒙皮宽度大于补片宽度的情况，采用式(19)、式(23)～式(27)以及均匀化方法(见图8)计算蒙皮刚度时，蒙皮宽度应取修理区宽度wR。

(28)

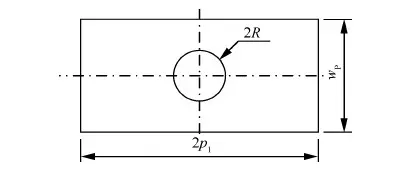
图8 开孔板几何尺寸Fig.8 Geometries of an open-hole plate

式中：ER为补片的轴向弹性模量。

2.2 螺栓等效刚度

关于螺栓的刚度，首先考虑单个螺栓的情形。文献[9-10，17]给出了不同的螺栓刚度计算方法，较常用的方法为Tate和Rosenfeld[9]和Nelson等[10]给出的方法。对于双面贴补修理，有

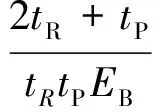
(29)

式中：GB为螺栓的剪切模量；EB为螺栓的弹性模量；AB为螺栓的横截面积；IB为螺栓的惯性矩。式(29)中第1项描述的是螺栓的剪切变形，第2项描述的是螺栓的弯曲变形，第3项描述的是螺栓的挤压变形，第4项和第5项分别描述的是搭接板和蒙皮的挤压变形。

Nelson等[10]将式(29)推广到单搭接接头的情况，有

(30)

相比式(29)，式(30)缺少第2项，并对后3项乘以一个因子1+3β。因子β描述了层压板与螺栓之间的接触力沿厚度方向的不均匀性所引起的弯曲效应占总弯矩的比例。弯矩的另外一部分由螺栓的头部或者螺母承担，即螺栓头部和螺母的作用效果用1-β表示。对于无侧边支撑的接头，如销钉连接，弯矩完全由孔边沿厚度方向的接触力承担，此时β=1，对于沉头螺栓可近似取0.5，对于带有螺栓头部和螺母的情况取值更小，当有较大的垫片且孔径/厚度比较大时，取值会更小。文献[10]中的垫片相对较小，孔径/厚度比d/t为 2.0，结果显示当采用β=0.15进行分析时，得到的载荷-位移曲线和试验结果吻合较好。

对于多列螺栓修理的接头，根据假设④，各排所有螺栓的位移相等，则各螺栓的钉载可表示为

(31)

(32)

式中：mi为第i(i=1,2,…,n)排螺栓的数目。将式(31)代入式(32)可得

(33)

(34)

由式(34)可以看到，对于规则排列的多列螺栓连接，螺栓刚度满足叠加原理，该排螺栓的等效刚度为各螺栓刚度之和。特别的，当螺栓参数相同时，式(34)可简化为

(35)

3 算 例

针对复合材料典型损伤的螺接修理问题，对模型进行考核，并通过有限元软件对模型有效性进行验证。

图9为T300/5208复合材料层合板螺栓修理接头的螺栓布局。损伤层压板长LP=160 mm，宽wP=80 mm，厚度tP=2 mm，损伤孔为圆形损伤，直径D=24 mm。损伤层合板的材料性能见表1，铺层顺序为[02/(±30)2/902]s，沿加载方向的等效刚度可由经典层合板理论得到，等效后EP=97.51 GPa。分别采用单面贴补和双面贴补两种修理方案。修理补片的材料为钛合金，长LR=124 mm，宽wR=60 mm，双面贴补中两补片厚度均为tR=1 mm，单面贴补中tR=2 mm。修理螺栓为钛合金螺栓，直径d=4 mm。修理方案为双排钉修理，排列形式为规则排列，螺栓沿宽度方向均匀分布，螺栓布局见图 9，共12个螺栓。

图9 双排钉螺接修理螺栓布局Fig.9 Pattern of bolts in double-column bolted repair joints

表1 损伤层合板的材料性能Table 1 Material properties of damaged laminate

螺接修理接头中的连接参数参考文献[17]中的设计，关于机械连接几何参数的选择规则见表2。根据本文选择的螺栓直径，螺接修理中的几何参数选择如下：排距p=20 mm，端距e=12 mm，列距S=20 mm，边距Sw=10 mm。

为验证分析模型的有效性，基于p型有限元技术[18]并采用文献[4，19]中提出的方法对接头进行有限元分析。复合材料螺接修理的有限元模型如图10所示。钉孔之间的挤压采用Fastener单元模拟，螺栓的弯曲/剪切刚度采用Link单元模拟，连接板采用平面应力单元模拟，忽略连接板的次弯曲效应，详见文献[19]。模型左端固支，右端施加均匀分布载荷，根据分析结果可以得到各螺栓的钉载比例以及传递到补片上的载荷。

首先基于光滑层压板方法、细观力学方法以及均匀化方法，计算得到了含损伤区段蒙皮的等效刚度，结果见表3。可以看到，细观力学和光滑层压板计算的等效刚度相差19%左右，说明开孔对蒙皮的刚度影响较为显著。均匀化方法与细观力学得到的刚度差异也接近20%，说明等效模型中引入的约束对等效刚度有较明显的影响。由于均匀化方法进行刚度等效时引入的周期性边界条件与损伤区的变形模式更接近，因此等效结果也更精确。

表2 螺栓连接中几何参数的选择[17]Table 2 Choice of geometry parameters in bolted joints[17]

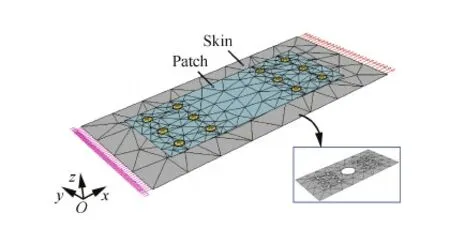
图10 螺接修理接头的有限元模型Fig.10 Finite element model for bolted repair joint

基于计算得到的蒙皮刚度，可分析得到传递到补片上的载荷比例。修理区和修理结构(修理区也可视为蒙皮和补片等宽的修理结构)传递到补片上的载荷如表4和表5所示。表4和表5同时给出了p型有限元的分析结果，可以看到，3种损伤区刚度的计算方法中，采用均匀化方法得到的损伤区刚度计算载荷传递比例时，预测数据和有限元分析结果最为接近，相对误差最大为7.7%。

对比表4和表5的结果可以发现，随着蒙皮宽度增加：

1) 传递到补片上的载荷比例减小。这主要是由于蒙皮宽度越大，蒙皮中非修理区参与承担的载荷越多，由式(18)计算的蒙皮非修理区刚度KUR越大，因此，根据式(16)，传递到补片上的载荷比例越小。

表3 损伤区蒙皮等效刚度Table 3 Equivalent stiffness of skin in damaged region 105 N·mm-1

表4 修理区传递到补片上的载荷比例

Notes: SLR—Single-lap repair; DLR—Double-lap repair； FEM—Finite element method.

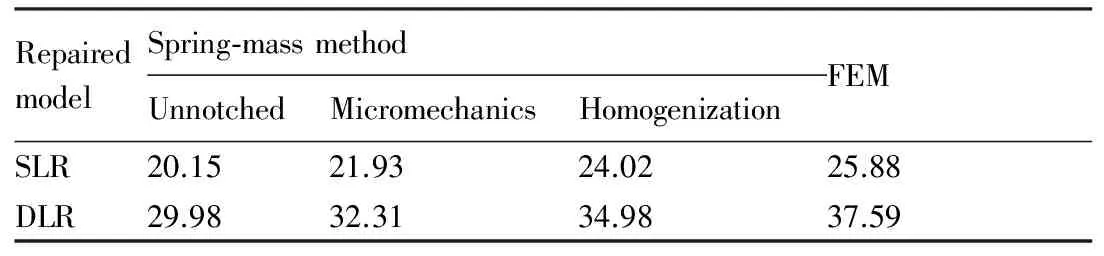
表5 修理结构传递到补片上的载荷比例

2) 预测数据和有限元之间的偏差减小。产生该现象的原因是在非修理区，蒙皮等效为光滑层压板，模型可“精确”计算该部分刚度。随着蒙皮宽度增大，该部分刚度在修理结构刚度的比例越大，即“精确”计算的部分越大，因此偏差会越小。

对比两种修理方式可以看到，对带损伤孔的层合板进行机械连接修理分析发现，相同补片厚度的情况下，双面修理传递到补片上的载荷较单面修理高45.3%，双面修理比单面修理有更高的传递效率。

本文提出的弹簧质量模型结构形式简单、计算简便、分析精度较高。模型所需参数具有解析的表达式或者通过简单的有限元计算(如损伤区蒙皮刚度均匀化方法计算)即可得到。模型建立的是线性方程组，求解不存在迭代等问题，计算几乎无条件限制，可用于复合材料螺接修理的快速设计。

4 结 论

1) 基于弹簧质量模型，提出了蒙皮和补片等宽情况下复合材料螺接修理钉传载荷比例的分析方法，并给出了蒙皮宽度与补片宽度不等情况下的修正方法。

2) 基于细观力学，推导得到了含圆形、椭圆形以及长圆孔形3种损伤时蒙皮损伤区等效刚度的计算公式。

3) 给出了采用均匀化方法计算含损伤蒙皮的等效刚度方法，并与细观力学、光滑层压板等方法得到的蒙皮刚度进行了对比。

4) 提出了螺栓等效刚度的概念，并证明了螺栓刚度的叠加原理，即对规则排列的螺栓连接结构，各排螺栓的等效刚度为该排各螺栓刚度之和。

5) 算例结果和有限元分析结果吻合较好，采用均匀化方法计算损伤区蒙皮的等效刚度，进而预测的载荷传递比例和有限元分析结果最为接近，相对误差最大为7.7%。说明本文提出的方法能够较准确地预测复合材料螺接修理结构的载荷传递比例。模型原理简单，为复合材料螺接修理设计提供了便捷的计算工具。

[1] 聂恒昌, 谭日明, 郭霞, 等. 复合材料层合板机械连接修理拉伸性能[J]. 北京航空航天大学学报, 2016, 42(2): 318-327.

NIE H C, TAN R M, GUO X, et al. Tensile performances of mechanically fastened repairs of composite laminates[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 318-327 (in Chinese).

[2] 杜奎, 黎增山, 何为, 等. 机械连接修理对圆孔应力集中系数影响研究[C]//第十四届中国科协年会第11分会场: 低成本、高性能复合材料发展论坛论文集. 北京: 中国科学技术协会, 2012: 22-27.

DU K, LI Z S, HE W, et al. The influence of mechanical connection repair for circle hole stress concentration coefficient[C]//Proceedings of the 14th Annual Meeting of China Association for Science Technology 11th Session: Forum on Development of Low Cost, High Performance Composite Materials. Beijing: China Association of Science and Technology, 2012: 22-27 (in Chinese).

[3] 赵美英, 万小朋, 刘浩. 复合材料螺接修补参数优化[J]. 航空学报, 2001, 22(5): 458-460.

ZHAO M Y, WAN X P, LIU H. Optimization of composite patch bolted repairing parameters[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(5): 458-460 (in Chinese).

[4] BORTMAN J, SZABO B A. Analysis of fastened structural connections[J]. AIAA Journal, 1992, 30(11): 2758-2764.

[5] SHI G Q, POON C, XIONG Y X. Finite element design and analysis of a bolted patch repair for composites[C]//42nd AIAA/ASME/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2001: 1-10.

[6] BARUT A, GUVEN I, MADENCI E. An analytical method for evaluating bolted joint repairs in composite structures[C]//52nd AIAA/ASME/ASC Structures, St-ructural Dynamics and Materials Conference. Reston: AIAA, 2011: 1-15.

[7] KRADINOV V, HANAUSKA J, BARUT A, et al. Bolted patch repair of composite panels with a cutout[J]. Composite Structures, 2002, 56(4): 423-444.

[8] ZHANG J M. Design and analysis of mechanically fastened composite joints and repairs[J]. Engineering Analysis with Boundary Elements, 2001, 25(6): 431-441.

[9] TATE M B, ROSENFELD S J. Preliminary investigation of the loads carried by individual bolts in bolted joints: NACA TN-1051[R]. Washington, D.C.: NACA, 1946.

[10] NELSON W D, BUNIN B L, HART-SMITH L J. Critical joints in large composite aircraft structures： NASA CR-3710[R]. Washington, D.C.: NASA, 1983.

[11] MCCARTHY M A, MCCARTHY C T, PADHI G S. A simple method for determining the effect of bolt-hole clearance on load distribution in single-column multi-bolt composite joints[J]. Composite Structures, 2006, 73(1): 78-87.

[12] MCCARTHY C T, GRAY P J. An analytical model for the prediction of load distribution in highly torque multi-bolt composite joints[J]. Composite Structures, 2011, 93(2): 287-298.

[13] 谢宗蕻, 李想, 郭家平, 等. 考虑间隙配合的复合材料钉载分配均匀化方法[J]. 复合材料学报, 2016, 33(4): 806-813.

XIE Z H, LI X, GUO J P, et al. Load distribution homogenization method of multi-bolt composite joint with consideration of bolt-hole clearance[J]. Acta Materiae Compositae Sinica, 2016, 33(4): 806-813 (in Chinese).

[14] HER S C, SHIE D L. The failure analysis of bolted repair on composite laminates[J]. International Journal of Solids and Structures, 1998, 35(15): 1679-1693.

[15] 康健. 基于均匀化方法的材料参数化优化设计研究[D]. 大连: 大连理工大学, 2006: 15-25.

KANG J. Parametric optimization design for material properties based-on homogenization method[D]. Dalian: Dalian University of Technology, 2006: 15-25 (in Chinese).

[16] HASSANI B, HINRON E. A review of homogenization and topology optimization II—Analytical and numerical solution of homogenization equations[J]. Computers & Structures, 1998, 69(6): 719-738.

[17] 谢鸣九. 复合材料连接手册[M]. 上海: 上海交通大学出版社, 2011: 132-133， 172-173.

XIE M J. Joints for composite materials book[M]. Shanghai: Shanghai Jiao Tong University Press, 2011: 132-133, 172-173 (in Chinese).

[18] SZABO B A, BASUKA I. Introduction to finite element analysis: Formulation, verification and validation[M]. West Sussex: John Wiley & Sons, Ltd., 2011: 145-165.

[19] ACTIS R L, SZABO B A. Analysis of bonded and fastened repairs by the p-version of the finite-element method[J]. Computers & Mathematics with Applications, 2003, 46(1): 1-14.

Acalculationmethodforloadtransferinboltedrepairofcompositelaminatesbasedonspring-massmodel

XIEZonghong1,*,LIXiang1,YANGLinya2,WUShi1

1.SchoolofAstronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.TheFirstAircraftInstitute,AviationIndustryCorporationofChina,Xi’an710089,China

Compositeboltedrepairprovidestheadvantagesofeasyoperation,fastprocessingandreliableperformance,makingitapreferablerepairmethodfordamagedcompositestructure,especiallyforbattledamagerepair.However,therepairdesignprocessiscomplex,anditisdifficulttomeettheneedforrapiddeterminationofparameters.Inthispaper,asimplemethodforestimatetheloadtransferincompositeboltedrepairisproposedbasedonthespring-massmodel.Theskinandthepatcharefirstassumedtobeofthesamewidth.Themodelisthenmodifiedandappliedtotheboltedrepairjointwherethewidthoftheskinislargerthanthatofthepatchbyintroducingtheprincipleofloadtransferinmaterialsaccordingtotheirstiffness.Thecalculationmethodforequivalentstiffnessofthedamagedskinisdiscussedintegratingthemicromechanicalmethodandthehomogenizationmethod.Thecalculationmethodfortheequivalentboltstiffnessisgivenandproventomeettheprincipleofsuperpositionforregulararrangementofbolts.Theproposedmethodisvalidatedbyapplyingittoanalyzetherepairofdamagedcompositeskinplatewithacircularhole.Themethodisalsocomparedwiththefiniteelementmethod(FEM).TheresultsshowthatthepredictedresultsbytheproposedmethodagreewellwiththosebytheFEM,withthemaximumerrorbeing7.7%.Themodelcouldbeusedforefficientandaccuratedesignandanalysisofcompositeboltedrepairjoint.

composites;boltedrepair;loadtransfer;boltloaddistribution;spring-massmodel

2016-06-07；Revised2016-07-06；Accepted2016-07-15；Publishedonline2016-08-150904

URL：www.cnki.net/kcms/detail/11.1929.V.20160815.0904.006.html

NationalNaturalScienceFoundationofChina(U1233202)

2016-06-07；退修日期2016-07-06；录用日期2016-07-15； < class="emphasis_bold">网络出版时间

时间：2016-08-150904

www.cnki.net/kcms/detail/11.1929.V.20160815.0904.006.html

国家自然科学基金 (U1233202)

*

.Tel.：029-88460405E-mailxzhae@nwpu.edu.cn

谢宗蕻， 李想， 杨淋雅， 等． 基于弹簧质量模型的复合材料螺接修理载荷传递计算方法J． 航空学报,2016,37(12):3742-3751.XIEZH,LIX,YANGLY,etal.Acalculationmethodforloadtransferinboltedrepairofcompositelaminatesbasedonspring-massmodelJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3742-3751.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0211

V214.8； TB330.1

A

1000-6893(2016)12-3742-10

谢宗蕻男， 博士， 教授， 博士生导师。主要研究方向： 复合材料结构分析与设计。Tel.： 029-88460405E-mail: xzhae@nwpu.edu.cn

李想男， 博士研究生。主要研究方向： 复合材料接头分析与设计。Tel.： 029-88460405E-mail: 895208876@qq.com

杨淋雅女， 硕士， 助理工程师。主要研究方向： 复合材料的多尺度分析与结构强度分析。Tel.： 029-86832811E-mail: gaoning91@163.com

吴师男， 硕士研究生。主要研究方向： 复合材料结构强度分析与设计。Tel.: 029-88460405E-mail: wuushi@foxmail.com

*Correspondingauthor.Tel.：029-88460405E-mailxzhae@nwpu.edu.cn