某中央翼盒对飞行载荷实测的影响

赵燕， 周占廷

1.中国飞行试验研究院 飞机所， 西安 710086 2.西北工业大学 航空学院， 西安 710072

某中央翼盒对飞行载荷实测的影响

赵燕1,2,*， 周占廷1

1.中国飞行试验研究院 飞机所， 西安 710086 2.西北工业大学 航空学院， 西安 710072

使用应变法测量某具有中央翼盒平尾的飞行载荷时，在地面校准试验中发现：左翼面载荷可使右翼面根部应变计有较大的响应，反之亦然。该现象可使根部载荷测量精度下降。分析了中央翼盒对根部载荷测量影响的机理，给出了一种考虑异侧载荷影响的载荷方程建立方法，讨论了不同类型剪力载荷方程对异侧载荷影响的敏感性，并将修正前后的方程应用于飞行载荷实测。结果发现：本文方法一定程度上可提高根部载荷方程的精度；对上述平尾结构，由两个剪力一个弯矩组建的载荷方程对异侧载荷影响不敏感，修正前后实测的飞行载荷差异在5.7%之内，由两个剪力和两个弯矩组建的载荷方程对异侧载荷影响敏感，修正前后实测的飞行载荷差异达到78.6%。

飞行试验； 翼根载荷测量； 应变电桥； 中央翼； 应变电桥的异侧载荷响应

在真实飞行环境下测量飞机结构承受的载荷称为飞行载荷实测，实测载荷可用于新机定型中载荷计算方法和设计余量的验证[1-2]、飞机疲劳载荷谱的编写[3-5]。相比较摄影录像[6]、光纤[7]和天平[8]等较新兴的测量仪器，应变电桥[9]和压力传感器[10]在实际工程中更为常用。先进压力传感器成本高，传统的传感器维护复杂，如不需要得到详尽压力分布，应变法可能更为经济适用。应变法由NASA提出，已应用到多种飞机进行了载荷实测，但其测量精度有时较差，仅地面检验误差有时就达到50%[11]。

使用应变法测量飞行载荷是一项十分复杂的工程项目，影响其测量精度的因素很多。William和Stauf[12]研究了地面校准试验中加载方式(单点和分布)、加载量级和工况数量等因素对载荷测量的影响。采用神经网络构建的非线性载荷方程[13-14]、基于遗传算法[15]及评估模型的建模方法[16]、“地面校准应变对飞行应变，地面校准载荷对飞行载荷”的映射方法[17]、有限元参与的混合建模[18]等在载荷模型的建立方法上做出了贡献。Jebacke和Horak[19]通过和静强度试验结果的比较，验证其应变法测量的正确性。文献[20]则考虑了飞行载荷测量的不确定度，更加客观地给出了应变法载荷测量精度的结果。

应变法通过结构变形间接测量飞机结构载荷，飞机自身结构形式也可影响载荷测量精度。通常翼面可视为连接在机身上的悬臂梁，翼面总载荷通过翼根传递给机身，为了测量翼面总载荷，应变计需加装在翼面根部。左侧应变计校准时，只设计左侧加载点，不考虑右侧加载，反之亦然。然而对于具有中央翼盒的翼面结构，由于中央翼盒连通了左右翼面，右侧加载时左根部应变电桥会有较大的响应，即本用于只感受左侧载荷的左根部应变计也感受了右侧载荷，载荷是应变的线性组合，这样左侧应变剖面测量到的左侧总载荷精度可能下降。因此本文将研究具有中央翼盒结构的翼面根部载荷测量。

1 中央翼盒的影响

1.1 应变电桥的异侧响应

用应变电桥进行飞行载荷测量的基本原理和详情见文献[9]。对于某具有中央翼盒连接的二梁平尾结构，垂直右平尾向下施加不对称单点载荷，共有8个加载工况，加载点或等效加载点分布如图1所示。所有工况的最大应变值如表1所示。8个单点不对称加载中，左侧应变桥均有响应，由于左平尾的外载荷为零，不会引起变形即应变值，可见该应变是由右侧的载荷引起的。将上述右翼面加载时左翼面应变电桥有响应的现象称为应变电桥的异侧响应。左右侧最大应变的比值M的绝对值范围为13.9%～62.3%。前梁剪应变是所有左侧应变中最大的，说明其受右侧载荷的影响最大。

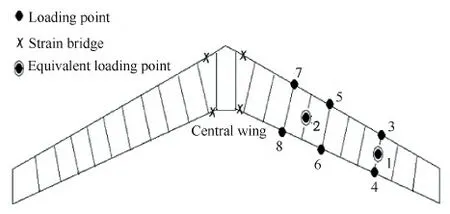
图1 某平尾不对称加载点分布 Fig.1 Unsymmetrical loading point distributions of certain horizontal tail

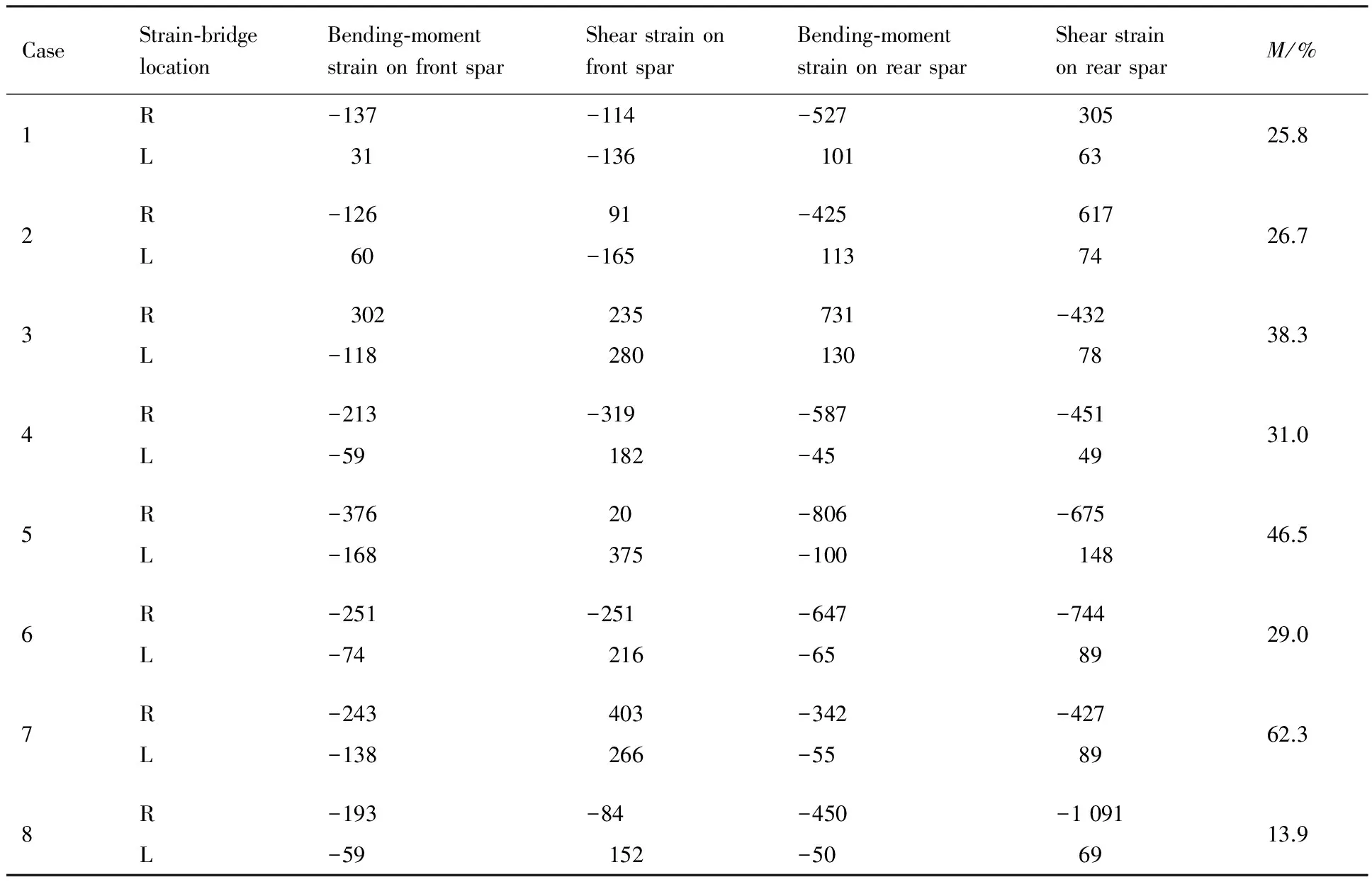
表1 某平尾不对称加载下左右剖面各应变电桥响应最大值之比(M)Table 1 Ratio of maximum left strain to maximum right strain (M) under unsymmetrical loading on certain horizontal tail

1.2 对响应系数的影响

应变电桥响应系数R[11]是单位载荷下的应变电桥响应，图1结构左侧4个应变电桥响应系数随加载坐标x的变化如图2所示，图2(b)数据扩大了常数倍，不影响问题分析。左加载点与右侧对称。左侧加载点坐标为正，右侧加载点坐标为负。

图2 左侧平尾应变电桥响应系数Fig.2 Response coefficients of strain bridge on left horizontal tail

左侧加载时左前梁弯矩电桥受单纯的弯矩载荷影响，后梁弯矩电桥呈现主要的弯矩特性，有少许的扭矩影响，两个剪力片电桥响应均受弯、剪和扭3种载荷的影响。右侧加载时，左后梁的两个应变电桥随异侧载荷位置的变化不明显，但左前梁弯矩和剪力电桥呈现出随加载距离增大而增大的异侧弯矩载荷特性，说明所有右侧加载对左前梁应变桥均有影响，且展向距离越大、影响越大。本用于只感受左侧载荷的左侧根部应变电桥，还感受了右侧的载荷。这样由左侧根部载荷方程(左侧根部应变桥线性组合)测量到的载荷就不是单纯的左侧载荷了，还混合了右侧载荷的影响。

2 中央翼盒影响的机理分析

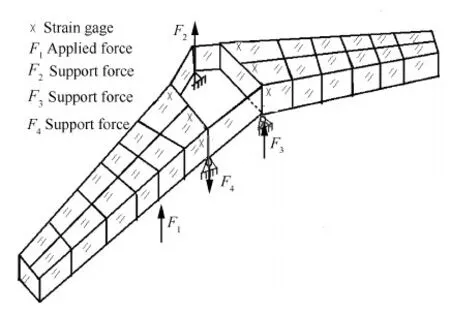
图3 某具有中央翼盒的平尾结构的不对称加载 Fig.3 Unsymmetrical loading on certain horizontal tail with central wing

依据飞行器结构力学，飞机翼面结构常简化为杆板式的空间薄壁结构，某具有中央翼盒的翼面结构简化示意如图3所示，前支撑(F2处)通过螺栓耳片连接在垂尾上，且有辅助的锁定机构，故前支撑简化为固支。后两个支撑(F3和F4处)只通过螺栓耳片连接在垂尾上且可转动，故简化为铰支。坐标原点在机头，x向为机身中轴线，由机头指向机尾为正，y向为飞机展向，指向右机翼为正。在左翼面施加一集中校准载荷F1，分析该结构的受力和变形。

按照传统受力分析，整个翼面所受载荷为校准载荷F1，3个支反力F2、F3和F4，4个集中力产生的弯矩Mx1、Mx2、Mx3和Mx4，4个集中力产生的扭矩My1、My2、My3和My4，则整个结构的平衡方程为

(1)

在该力系内，弦向剖面弯矩、剪力和扭矩不为0，但该力系之外的翼剖面的弯矩、剪力和扭矩为0。将右翼应变电桥剖面之外的部分整体隔离，作为受力分析对象,如果该剖面的弯矩、剪力和扭矩不为0，那么没有载荷与之平衡，与结构力学受力分析矛盾，即左侧的载荷没有转移到右侧。

中央翼盒后梁右支撑F3的局部如图4所示，将结构离散为拉格朗日型的网格，网格尺寸足够小，可随着结构的变形而变形。实线网格为变形之前的结构，虚线为变形之后的结构。

在式(1)所述的载荷作用下，左侧网格I有变形，2、7和8点有位移，由于约束，1点没有位移，假设I网格的右边界由1-8变为1′-8′，III网格的左边界仍保持为1-8，则意味着出现断裂，与变形之后结构是连续的矛盾。同理在网格III左边界变形的作用下右侧网格III和IV均会变形。与支反力F3右侧结构变形类似，支反力F2右侧结构也有变形，这样右外翼3个方向均可能会有变形，因此粘贴在右外翼的应变电桥有响应。中央翼盒处转移效应是结构自身变形连续性导致的，空中飞行时仍然存在。

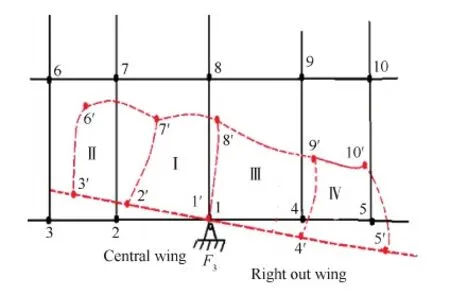
图4 中央翼盒处局部变形示意图Fig.4 Schematic diagram of local deformation at central wing

3 考虑中央翼盒影响的应变电桥校准

3.1 地面校准试验

某平尾的右侧根部共加装了6个应变桥，类型有弯矩、剪力和扭矩。将飞机3个起落架约束固定在地面上，使用液压作动器对飞机的平尾进行点校准加载。不考虑中央翼盒引起的应变计异侧载荷响应时，为了加载系统平衡，左右翼面同时进行对称加载。为了考察左右翼面载荷的交互影响，分别设计了左右不对称加载。共进行了14个单点对称加载、6个单点左侧加载、6个单点右侧加载、2个对称组合加载、2个不对称组合加载、2个基于线性叠加原理得到的多点不对称组合加载。记录上述加载下的载荷和应变电桥响应。

3.2 考虑中央翼盒影响的载荷方程建立

文献[9]直接给出了建立载荷方程的列式，没有分析其列式是否可消除中央翼盒对根部载荷测量的影响，且其列式中使用了左右根部两侧的应变电桥。本文将基于线性叠加原理，推导一种可消除中央翼盒影响的载荷方程，且只使用单侧应变电桥。

使用式(2)建立载荷方程，L为弯矩、剪力或扭矩的一种，k1,k2,…,kn为待求解的载荷方程系数，μ1,μ2,…,μn为剖面应变电桥响应，n为应变电桥序号。

L=k1μ1+k2μ2+…+knμn

(2)

对于右侧根部载荷测量，尽管加载时左侧根部应变电桥有响应，但其影响对右侧根部内力没有贡献。另外实际飞行中受外界环境的影响，每个应变电桥均可能出故障或坏掉，使用的应变电桥个数越多，受影响的因素就越多。所以右侧根部载荷测量时只使用右侧应变电桥。

对于某具有中央翼盒的右侧根部剖面，同时考虑左右加载时，依据线性叠加原理，总载荷L为左右翼面的载荷总和，应变电桥响应值为左右侧翼面载荷引起的应变总和，即

L=LR+LL

(3)

(4)

式(3)和式(4)中：LR和LL分别为右侧翼面和左侧翼面载荷；μ1,R,μ2,R,…，μn,R为LR引起的应变响应；μ1,L,μ2,L,…，μn,L为LL引起的应变响应。将式(3)和式(4)代入式(2)，则式(5)成立。

LR+LL=k1(μ1,R+μ1,L)+k2(μ2,R+μ2,L)+…+

kn(μn,R+μn,L)

(5)

将式(5)右端改写，则有式(6)成立。

LR+LL=(k1μ1,R+k2μ2,R+…+knμn,R)+

(k1μ1,L+k2μ2,L+…+knμn,L)

(6)

式(6)左端LR为目标载荷，LL为引入的误差，希望其为0， 式(6)右端第1项为目标应变线性组合，第2项为引入的误差，希望其为0，因此可得到满足式(6)成立的一个充分条件，即

(7)

若式(7)成立，式(7)中的两式相加，则有

LR=k1(μ1,R+μ1,L)+k2(μ2,R+μ2,L)+… +

kn(μn,R+μn,L)

(8)

虽然右侧应变电桥感受到了左侧载荷，μ1,L≠0,μ2,L≠0,…,μn,L≠0，但由于式(7)的第2个式子成立，仍可测到准确的右侧载荷，即式(8)成立。式(7)为消除左侧载荷影响的列式。

式(7)是基于不对称加载得到的列式，理论上依据叠加原理由式(7)可得到对称加载应变响应，但从样本空间的视角考虑，若使地面校准的样本空间尽可能覆盖空中实际飞行的对称和不对称状况，建立载荷方程时也应考虑对称加载的工况。因此本研究中考虑中央翼盒影响的载荷方程模型为

(9)

式中：LR,uns为右侧不对称加载的载荷；μ1R,uns,μ2R,uns,…,μnR,uns为LR,uns加载下右侧应变电桥响应；μ1L,uns,μ2L,uns,…,μnL,uns为左侧不对称加载下的右侧应变电桥响应；Lsym为对称加载工况中的右侧载荷；μ1,sym,μ2,sym,…，μn,sym为对称加载下的右侧应变响应。

3.3 修正前后载荷方程的差异

不考虑中央翼影响时，使用式(9)中的第1个式子建立剪力方程，考虑中央翼盒影响时，使用式(9)建立剪力方程。本研究的目的为研究中央翼盒对根部载荷测量的影响，不是方程类型的确定，为了更加客观地展示修正后的结果，对于该种结构，给出了如表2所示的常使用的3类典型方程，使用两个剪力和一个弯矩建立的方程称为A型，使用两个剪力和两个弯矩建立的方程称为B型，使用两个剪力、两个弯矩和两个扭矩建立的方程称为C型，μB1、μB2、μS1、μS2、μT1和μT2分别为前后梁的弯矩、剪力和扭矩电桥。使用2个对称工况(Symmetrical case 1, Symmetrical case 2)、2个20%不对称工况(一侧为另一侧载荷的80%：20% unsymmetrical case 1, 20% unsymmetrical case 2)和2个100%不对称工况(一侧加载，一侧载荷为0：100% unsymmetrical case 1, 100% unsymmetrical case 2)3类工况进行检验。检验误差(Validation Error，VE)如表3所示。为叙述方便，考虑中央翼盒影响前的简称修前(Before)，考虑中央翼盒影响后的简称修后(After)。

表2 修正前后的剪力方程Table 2 Shear equations before and after correction

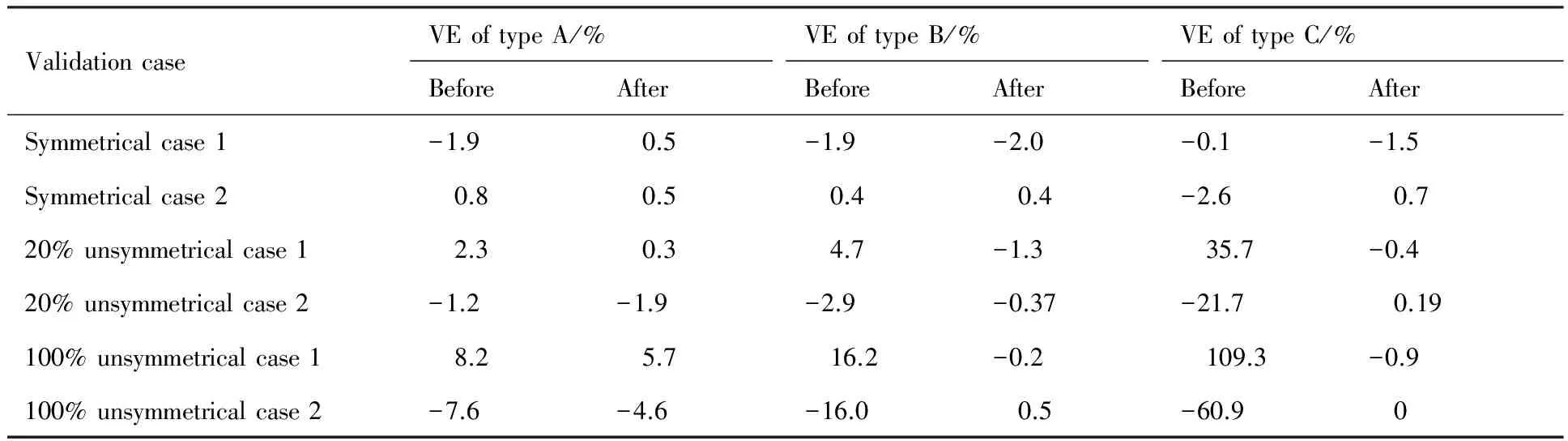
表3 修正前后剪力方程在不同类检验工况下的检验误差Table 3 Validation error (VE) of shear equations before and after correction in different validation cases

对称检验中修前的误差绝对值为0.1%～2.6%、修后的误差绝对值为0.4%～2.0%。20%不对称检验中修前的误差绝对值为1.2%～35.7%、修后的误差绝对值为0.2%～1.9%。100%不对称检验中修前的误差绝对值为7.6%～109.3%、修后的误差绝对值为0%～5.7%。可看出随不对称程度的增加，修前的检验误差逐步增大，高达109.3%，修后的误差均较小，在5.7%以内，验证了3.2节所推导的引入方式是可行的。A型修前、修后的方程在对称、20%不对称和100%不对称检验时的检验误差变化不大，在3.0% 之内，一定程度上说明该类型剪力方程对中央翼盒处转移效应不是很敏感。B型修前、修后的方程在对称、20%不对称检验时误差变化较大，在15.0%之内。C型修前、修后的方程在对称、20%不对称检验时误差变化最大，可达100%以上，在3类剪力方程中对转移效应最敏感。

4 实测飞行载荷的差异

在某高度、某马赫数下，先稳定平飞，进行横向操纵使飞机建立稳定盘旋，当飞机倾斜角达到右侧45° 时，反向操纵使飞机迅速向相反方向滚转，倾斜角达到左侧45°，测量上述机动过程中平尾根部应变剖面的滚转机动飞行载荷。图5为不同载荷方程实测的滚转机动剪力S和滚转角θ，图5(a)为A型方程实测的左右剪力S，左侧剪力减小，右侧剪力增大，两侧A型方程修正前后差异均较小，在5.7%之内，验证了对于该飞机的校准数据，A型剪力方程对中央翼盒的影响不敏感。图5(b)为B型方程实测的左右剪力S，B型方程修正前后实测载荷差异较大，达到78.6%，也验证了B型的剪力方程对中央翼盒的影响较敏感,与地面校准试验中的中央翼盒影响敏感性分析结果一致。由于扭矩电桥在飞行试验中损坏，故此处没有C型方程的飞行结果。

图5 不同方程测量的飞行滚转剪力Fig.5 Flight shears from different types of load equations in rolling maneuver

5 结 论

1) 使用应变电桥测量飞行载荷时，发现中央翼盒的连通作用可降低某平尾根部载荷测量精度，其是由结构的连续变形引起的。

2) 对于某具有中央翼盒的平尾结构，随着检验工况不对称程度的增加，部分修前的检验误差逐步增大，高达109.3%，修后所有剪力方程的检验误差在5.7%以内，一定程度上本文给出的消除中央翼盒对根部飞行载荷测量影响的方法是可行的。

3) 对于某具有中央翼盒的平尾结构，由两个剪力一个弯矩组建的剪力方程对中央翼盒的影响不敏感，修正前后实测的飞行载荷差异在5.6%之内，由两个剪力和两个弯矩组建的剪力方程对中央翼盒的影响敏感，修正前后实测的飞行载荷差异达到78.6%。

致 谢

感谢西北工业大学万小朋教授对本文的指导，感谢中国飞行试验研究院飞行载荷研究室的全体人员在试验过程中付出的努力。

[1] 中国民用航空局. 中国民用航空规章： CCAR—25—R4[S]. 北京： 中国民用航空局, 2011.

Civil Aviation Administration of China. Chinese civil aviation regulations: CCAR-25-R4[S]. Beijing: Civil Aviation Administration of China, 2011 (in Chinese).

[2] 总装备部. 军用飞机强度和刚度规范， 第十部分： 飞行试验: GJB67.10A—2008[S]. 北京： 总装备部军标出版发行部， 2008: 1-10.

General Equipment Department. Military airplane structural strength specification Part 10: Flight tests: GJB67.10A-2008[S]. Beijing: General Equipment Department Military Standard Press, 2008: 1-10 (in Chinese).

[3] 阎楚良, 高镇同. 飞机高置信度中值随机疲劳载荷谱的编制原理[J]. 航空学报, 2000, 21(2): 118-123.

YAN C L, GAO Z T. Compilation theory of median stochastic fatigue load spectrum with high confidence level for airplane[J]. Acta Aeronautica et Astronautics Sinica， 2000, 21(2): 118-123 (in Chinese).

[4] LESKI A, REYMER P, KURDELSKI M. Development of load spectrum for full scale fatigue test of a trainer aircraft[C]//Proceedings of the 26th Symposium of International Commitlee on aeronautical Fatigue. Netherland: Springer, 2011.

[5] PIOTR R， ANDRZEJ L. Flight loads acquisition for Pzl-130 OrLik TCII full scale fatigue test[J]. Fatigue of Aircraft Structures， 2011(1): 78-85.

[6] LIZOTTE A M, LOKOS W A. Deflection-based aircraft structural loads estimation with comparation to flight[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2005.

[7] BAKALYAR J. Validation tests of fiber optic strain-based operational shape and load measurements[C]//20th AIAA/ASME/AHS Adaptive Structures Conference. Reston: AIAA, 2012.

[8] 郭正旺, 李昭广， 王仲燕, 等. 用内式六分量应变天平实测导弹挂飞载荷[J]. 航空学报， 2010， 31(7): 1403-1409.

GUO Z W, LI Z G, WANG Z Y, et al. Measuring missile’s suspension flight loads using built-in six-compoment strain-gage balance[J]. Acta Aeronautica et Astronautics Sinica, 2010, 31(7)： 1403-1409 (in Chinese).

[9] SKPOINSKI T H， AIKEN W S， HUSTON W B. Calibration of strain-gage installations in aircraft structures for measurement of flight loads: NACA-TR-1178[R]. Washington, D.C.: NASA, 1954.

[10] KWAK D Y, YOSHIDA K. Flight test measurements of surface pressure on unmanned scaled supersonic experimental airplane[C]//24th Applied Aerodynamics Conference. Reston: AIAA, 2006.

[11] JENKINS J M, DEANGELIS V M. A summary of numerous strain-gage load calibrations on aircraft wings and tails in a technology format: NASA-TM-4804[R]. Washington, D.C.: NASA, 1997.

[12] WILLIAM A, STAUF L R. Strain-gage loads calibration parametric study: NASA/TM-2004-212853[R]. Washington, D.C.: NASA, 2004.

[13] CAO X, SUGIYAMAC Y, MITSUIi Y. Application of artificial neural networks to load identification[J]. Computer & Structures, 1998, 69: 63-78.

[14] HALLE M, THIELECKE F. Flight loads estimation using local model networks[C]//29th Congress of the International Council of the Aeronautical Sciences. BONN: ICAS, 2014

[15] NELSON S A. Strain gage selection in loads equations using a genetic alogrithm: NASA Contractor Report 4597[R]. Washington, D.C.: NASA, 1994.

[16] 赵燕. 基于遗传算法与评估模型的飞行载荷实测研究[J]. 航空学报， 2014, 35(9): 2506-2512.

ZHAO Y. Flight load measurement based on genetic algorithm and evaluating method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2506-2512 (in Chinese).

[17] PADMANABHAN M A, NAGESH K Y, Elattuvalappil H. A statistcs based method for mapping flight strains to loads[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2006.

[18] JASON D B, JOAO C M. Hybrid load calibrations of a strain gage instrumented horizontal empennage[C]//VI National Congress of Mechanical Engineering. Compina: CONEM, 2010.

[19] JEBACKE I, HORAK M. Possibilities and methods of in-flight loading measurement[J]. Aviation, 2012, 16(2): 47-50.

[20] GONZALEZ M, GOGU C, BINAUD N, et al. Uncertainty quantification in aircraft load calibration[C]//10th World Congress on Structural and Multidisciplinary Optimization. East Lansing: WCSMO, 2013.

Effectofcentralwingonrootflightloadmeasurementofcertainairfoil

ZHAOYan1,2,*,ZHOUZhanting1

1.InstituteofAircraft,ChineseFlightTestEstablishment,Xi’an710086,China2.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Forflightloadmeasurementusingstraingageofcertainhorizontalstabilizerwithcentralwing,ithasbeenfoundthatrightrootstrainresponseislargewhenloadingleftairfoilingroundcalibrationtest,andviceversa,whichcouldlowerflightloadmeasurementaccuracy.Themechanismofcentralwingeffectsonrootflightloadmeasurementwasanalyzed.Alsoamethodofeliminatingoppositeloadeffectsonflightloadmeasurementwasproposed.Further,thesensitivityofdifferenttypeloadequationstooppositeloadeffectswasdiscussed.Moreover,thecorrectedloadequationswereusedtomeasureflightloads.Theresultsshowthatforabovehorizontaltailwithcentralwing，theproposedmethodinthispapercouldimproverootloadequationaccuracy.Thebuiltshearloadequationusing2shearand1bending-momentstrainbridgesisnotsensitivetooppositeloadeffectswherethemeasuredflightshearsthroughloadequationsbeforeandaftercorrectionhavedifferencesunder5.7%,whilethebuiltshearloadequationusing2shearand2bending-momentstrainbridgesissensitivetooppositeloadeffectswherethemeasuredflightshearusingloadequationsbeforeandaftercorrectionhavelargedifferencesof78.6%.

flighttest;rootflightloadmeasurement;strainelectricalbridge;centralwing;strainresponseonoppositeload

2016-01-20；Revised2016-02-19；Accepted2016-03-29；Publishedonline2016-04-221012

2016-01-20；退修日期2016-02-19；录用日期2016-03-29； < class="emphasis_bold">网络出版时间

时间：2016-04-221012

www.cnki.net/kcms/detail/11.1929.V.20160422.1012.004.html

*

.Tel.：029-86830410E-mailzhaoyan1031@mail.nwpu.edu.cn

赵燕， 周占廷． 某中央翼盒对飞行载荷实测的影响J． 航空学报,2016,37(12):3713-3720.ZHAOY,ZHOUZT.EffectofcentralwingonrootflightloadmeasurementofcertainairfoilJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3713-3720.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0105

V215.1

A

1000-6893(2016)12-3713-08

赵燕女， 博士， 高级工程师。主要研究方向： 飞行载荷与强度。Tel.: 029-86830410E-mail: zhaoyan1031@mail.nwpu.edu.cn

周占廷男， 本科， 研究员。主要研究方向： 飞行载荷与强度， 系统工程。Tel.: 029-86836259E-mail: zhouzhanting@126.com

URL：www.cnki.net/kcms/detail/11.1929.V.20160422.1012.004.html

*Correspondingauthor.Tel.：029-86830410E-mailzhaoyan1031@mail.nwpu.edu.cn