亚轨道飞行器发动机故障下配平能力分析
王文虎, 韩冰
中北大学 机电工程学院, 太原 030051
亚轨道飞行器发动机故障下配平能力分析
王文虎*, 韩冰
中北大学 机电工程学院, 太原 030051
为了分析亚轨道飞行器发动机故障下配平能力,将配平能力问题转换为线性等式/不等式混合方程组相容性判定问题。提出了将基于顶点投影法的相容性判定方法用于配平能力分析,验证了方法的准确性与计算效率。在故障下配平能力分析的总体框架下,分别对不同故障模式下故障发生时刻、整个空域配平能力进行分析,给出了配平能力不足时的应急策略。仿真结果表明,该方法能够快速地计算故障下不可配平区域、分析配平能力对可飞区域的影响,对故障后任务中止策略、任务中止轨迹优化等研究具有重要的参考价值。
亚轨道飞行器; 发动机故障; 配平能力; 相容性判定; 混合方程组
发动机是亚轨道飞行器(Suborbital Reusable Launch Vehicle, SRLV)较易发生故障的关键部件[1-3]。SRLV发动机故障下,快速有效地判断故障飞行器的控制配平能力对飞行安全至为重要。
亚轨道飞行器上升段控制的执行机构为摆动发动机[4],若发生故障,必然会造成控制力矩的损失,严重情况下可能导致控制配平能力不足,影响飞行任务的安全性。有必要根据故障模式、当前的飞行状态,判断是否能够配平、分析配平不足时的应急策略及配平能力下降对飞行约束的影响。因此,配平能力分析也是故障下任务中止决策的重要依据之一[5]。
针对重复使用运载器执行机构故障下配平能力问题,国内外学者进行了相关的研究。美国海军研究生院Ross与空军研究实验室Doman等对X-33进场着陆段气动舵面故障下容错最优轨迹进行了研究,并通过配平能力分析将故障对六自由度模型的影响引入至三自由度模型中[6-9]。西北工业大学解永锋采用非线性控制分配算法进行了SRLV返回段气动舵面故障下配平特性计算[10]。文献[11-13]采用可变单纯形法、线性规划法、序列二次规划方法进行配平能力分析。本质上,上述方法均为基于数值优化的方法,这类方法容易收敛到局部最优解,同时求解时间也相对较长。
本文首先通过简化,将SRLV配平能力问题转化为线性等式/不等式混合方程组相容性判定问题,提出了基于顶点投影法的相容性判定方法用于配平能力分析。然后,给出了SRLV发动机故障下配平能力分析总体框架,并针对不同故障模式从故障发生时刻配平能力分析和整个空域配平能力分析2个方面进行了研究。
1 SRLV配平问题描述与简化
1.1 配平问题描述


图1 SRLV发动机配置示意图Fig.1 Schematic diagram of SRLV engine arrangement
为实现飞行器的转动配平,双摆发动机产生的力矩ME与气动舵产生的力矩MA之和必须抵消掉机体产生的期望配平的气动力矩Mdes。
通过推导可得,ME在体坐标系各轴上的分量即滚动、偏航、俯仰力矩为
(1)
式中:
式中:P1、P2分别为1#、2#发动机的推力大小;rc为发动机铰链位置至SRLV纵向对称平面xbobyb的距离。
MA、Mdes可由气动力矩公式得到,均与动压、马赫数、攻角等有关,并且在这些飞行状态已知的情况下,气动舵面操纵力矩MA是舵偏角δe、δr、δa和δbf的非线性函数。
令发动机摆角/气动舵偏角向量

(2)
且δ的摆动极限位置向量分别为δmax、δmin。则判断能否配平可描述为是否存在发动机摆角/气动舵偏角向量δ,使得满足
(3)
可见,在其他飞行状态给定的情况下,式(3)为关于δ的有约束非线性方程组。
配平问题本质上是一个控制分配问题。由于SRLV发动机摆角/气动舵偏角个数大于受控变量即操纵力矩(俯仰、偏航和滚转通道力矩)的个数,故存在一定的控制冗余度,可以由控制分配算法求解。控制分配算法在给定性能指标的前提下,不仅能够检验飞行器能否配平,还能给出发动机摆角的最优组合。但常见的控制分配算法都是基于优化的,计算时间较长,并且算法的误差也可能导致配平能力的误判。本文的配平能力分析只期望能够在发生故障下快速地判断飞行器能否配平。因此,可通过判断式(3)解的存在性来检验飞行器能否配平。若式(3)有解,则飞行器能够配平,反之则不能配平。
1.2 配平问题简化
由于主发动机喷管摆动角度较小(±10°以内),为便于分析计算,可取
(4)
考虑到气动数据离散的存储在多维插值表中,因此可利用原始气动数据,将舵面气动力矩与舵偏角之间存在的非线性关系进行分段线性化。
假定分段线性化后舵偏角分段组合个数为K,则对第k个舵偏角分段组合,式(3)可简化为
(5)
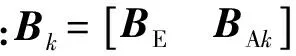
(6)
式中:BAk为第k分段气动舵效率矩阵;δkmin、δkmax为第k个分段摆角/气动舵偏角极限位置,可根据发动机摆角位置约束与原始气动数据分段情况得到。且有
(7)
式中:Mx、My和Mz分别为机体产生的滚动、偏航和俯仰气动力矩,即Mdes在体坐标系下的分量。
在分类算法方面,本文对比了GMM算法,支撑矢量机(SVM)和BP神经网络(ANN)算法。实验仍然采用K-交叉验证法,实验结果如图5所示。由图5可知,3种算法中,GMM算法的效果最佳,最差的神经网络算法。SVM算法本身对于多分类问题的效果不佳,而ANN算法对网络结构的要求较高,因此基于概率的GMM算法的有效性更好。
至此,配平能力分析问题转化为如式(5)所示线性等式/不等式混合方程组相容性判定问题。若K个分段中只要存在1个分段使式(5)有解(相容),则飞行器能够配平,否则不能配平。
配平问题的简化是将问题线性化的过程。为使该方法更具实际工程应用价值,发动机喷管摆动角度越小、气动数据离散点越密,越能满足线性化条件。考虑到现有运载火箭二级以上基本采用带小喷管的游动发动机控制飞行姿态,小喷管最大摆角可达60°,线性化条件不能满足。因此,本文方法不适用于采用游机控制的重复使用运载器。
2 基于顶点投影法的相容性判定方法
为了与本文研究内容相对应,考虑如下形式线性等式/不等式混合方程组
(8)
式中:A的元素为aij(i=1,2,…,m;j=1,2,…,n);b=(b1,b2,…,bm)T;x=(x1,x2,…,xn)T;xl=(x1l,x2l,…,xnl)T;xu=(x1u,x2u,…,xnu)T。
若要判断该方程组的相容性,一种思路是先将线性等式/不等式方程组转化为线性不等式方程组,然后通过判定线性不等式组围成的凸空间是否为空来进行相容性判定。判定线性不等式组围城的凸空间是否为空可通过交边算法、位置算法或梯度算法进行求解[16-18],但这类方法需要先将线性等式方程组转化为不等式方程组,会降低计算效率。
本文提出一种新的基于顶点投影法的线性等式/不等式方程组相容性判定方法。该方法不需要将等式方程转化为不等式方程,根据线性等式方程组解的形式对问题分类处理,通过n维线性空间中,点到超平面投影及超长方体顶点与其投影点构成的空间向量等手段判断超平面与超长方体的空间位置关系,从而对线性等式/不等式方程组相容性进行判定。
令集合S={x|Ax=b,x∈Rn},则当S不为空时,表示由Ax=b所确定的n维线性空间的点、直线或超平面。令集合D={x|xl≤x≤xu,x∈Rn},则D表示n维空间内某一超长方体(D≠∅)。若S∩D≠∅,则式(8)相容(有解),否则不相容(无解)。
为了便于理解算法流程,先对n维线性空间点到超平面投影计算方法及通过超长方体顶点与其投影点构成的空间向量判断相容性等问题进行探讨。
1)n维线性空间点到超平面投影计算方法
若线性等式方程组Ax=b所确定的超平面为S,假定n维线性空间内任意一点为x0=(x10,x20,…,xn0)T。若需求点x0在超平面S内的投影点,则令超平面内一点x与x0间距离d最短,有
(9)
而Ax=b可视为线性等式约束,则令
(10)
式中:λi为拉格朗日乘子。则由极值条件可得
(11)
由式(11)可得
(12)
将式(12)代入Ax=b,令λ=(λ1,λ2,⋮λm)T可得

(13)
则有
λ=2(AAT)-1(Ax0-b)
(14)
代入式(12)得
x=x0-AT(AAT)-1(Ax0-b)
(15)
注意到当A不为行满秩情况下,(AAT)-1不存在。为使方法适用于任意矩阵A,引入广义逆矩阵概念,即有
x=x0-AT(AAT)+(Ax0-b)
(16)
对于加号逆,有性质A+=AT(AAT)+,故x0在超平面S内的投影点x为
x=x0-A+(Ax0-b)
(17)
该方法不需要求解方程组Ax=b,可直接由式(17)计算得到n维线性空间点到超平面投影坐标。
2) 相容性判定准则及其证明
相容性判定准则:设超长方体D的顶点为Zk(k=1,2,…,2n),任取一顶点Zk,其在超平面S上的投影为P,P与所有顶点构成的向量为Wk=PZk(k=1,2,…,2n)。若除Wk外所有空间向量W1,W2,…,Wk-1,Wk+1,…,W2n中只要有一个使得其与向量Wk的内积小于或等于零,则超长方体D与超平面S相交,即S∩D≠∅。否则,S∩D=∅。这条判定准则也适用于任意凸多面体。
证明:
(18)
则有
[Wk,Wl]=[Wk,WPQ+WQZl]=
[Wk,WPQ]+[Wk,WQZl]≤0
(19)
当Zk与其投影点P重合时,Zk与P构成的向量Wk=0,有[Wk,WPQ]=0;当Zk与P不重合时,Wk为超平面S的法向量,而P与Q点均在超平面S内,故有Wk⊥WPQ,即[Wk,WPQ]=0。由式(19)可知:[Wk,WQZl]≤0。可分两种情况考虑:
① [Wk,WQZl]=0
当[Wk,WQZl]=0时,可得Wk=0或WQZl=0或Wk⊥WQZl。若Wk=0或WQZl=0分别可得超长方体顶点Zk或Zl在超平面S内,则S∩D≠∅。若Wk⊥WQZl,而Q点在超平面S内,则Zl必在超平面S内,故S∩D≠∅。
② [Wk,WQZl]<0
当[Wk,WQZl]<0时,Wk、WQZl均不为0且方向相反,P与Q均为投影点,而Wk、WQZl为超平面S的法向量,因此超长方体顶点Zk与Zl必在超平面S的两侧,可得超平面S必与超长方体D相交,即S∩D≠∅。
综上所述,当[Wk,Wl]≤0时,S∩D≠∅。
证毕.
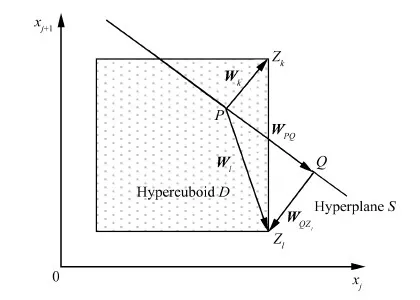
图2 相容性判定准则示意图Fig.2 Schematic diagram of compatibility decision criterion
2.2 算法流程
图3给出了基于顶点投影法的线性等式/不等式混合方程组相容性判定流程,具体算法如下:
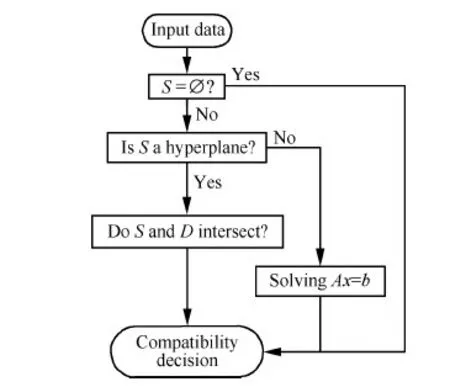
图3 相容性判定流程图Fig.3 Flowchart of compatibility decision
1) 判断S是否为空
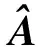
2) 判断S是否为超平面
若rankA≥n-1,求解线性方程组Ax=b。当rankA=n时,Ax=b存在唯一解x*,判断x*是否在集合D内,若x*∈D,则等式/不等式方程组相容,否则不相容,程序返回。当rankA=n-1时,Ax=b有无穷多解,通解为x*=η*+kξ(k∈R),ξ为齐次线性方程组Ax=0。判断其特解η*是否在集合D内,若η*∈D,则等式/不等式方程组相容,程序返回;否则,令xl≤x*≤xu,则可得xl≤η*+kξ≤xu,这是一个关于实数k的不等式方程组,可通过不等式性质求解,若该不等式方程组相容,则等式/不等式方程组相容,否则不相容,程序返回。
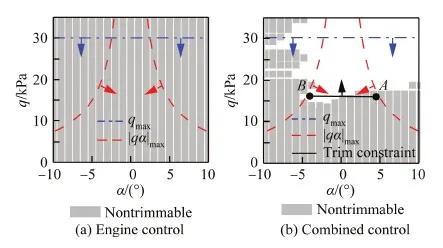
若rankA 3) 判断S是否与超长方体D相交 通过已证明的相容性判定准则判断S是否与超长方体D相交,若相交则等式/不等式方程组相容,否则不相容,程序返回。 2.3 相容性判定计算效率 为了验证所提出方法的计算效率,针对不同规模线性等式/不等式混合方程组,分别采用单纯形法、交边算法及本文提出的方法进行了相容性判定。 表1为相容性判定方法计算效率比较结果。可以看出,对于较大规模问题,本文方法也能快速地对问题的相容性进行判定,计算效率要高于单纯形法及交边算法。 表1 方法计算效率验证Table 1 Verifying method’s efficiency 3.1 故障下配平能力分析总体框架 为使读者对后面内容有一个全局了解,图4给出了故障下配平能力分析的总体框架。 图4 配平能力分析总体框架Fig.4 Framework of trim capacity analysis 主要从2个层面对故障下配平能力进行分析,包括:故障发生时刻配平能力分析和整个空域内配平能力分析。 故障发生时刻配平能力分析是利用故障发生时刻飞行状态对当前飞行器控制配平能力进行分析,目的是在控制能力不足时快速做出应急策略。正常飞行上升段采用摆动发动机单独控制,在给定故障模式与故障发生时刻条件下若不能配平,则采用发动机/气动舵复合控制策略,若复合控制仍不能配平,则需要采取某些配平不足应急策略以满足控制配平需求。若故障下两种控制策略能够实现配平,则表明故障点附近飞行器具有控制配平能力,但不代表在整条飞行轨迹上能够配平,由于故障可能会导致飞行轨迹与正常飞行情况有较大变化,因此有必要对故障下整个空域内配平能力进行分析。 整个空域内配平能力分析是针对不同故障模式对选定的飞行状态区域内所有点进行控制配平能力进行分析,目的是分析由于故障引起的配平能力下降对飞行包络及飞行约束的影响。 因此,故障发生时刻配平能力分析可看作为一种短时效的配平能力分析,只对当前状态附近点有效,可为故障时刻控制能力分析提供参考;整个空域内配平能力分析可看作为一种长时效的配平能力分析,对故障后整个飞行轨迹上状态点均有效,可为故障后任务规划、轨迹重构及制导等提供依据。 3.2 故障发生时刻配平能力分析 1) 正常飞行情况 为便于后面故障下配平分析并验证提出的判定方法,图5给出了正常飞行情况有动力上升段攻角α、马赫数Ma、飞行高度H、动压q等状态随飞行时间t变化曲线,同时利用提出的方法对无故障下正常飞行轨迹上各飞行时刻进行配平分析,结果表明不同飞行时刻均能够实现配平,单个数据点平均配平计算速度在10-4s量级。 2) 单台发动机推力损失情况 若单台发动机发生故障,则故障发动机推力的下降以及由于故障后两台发动机推力不相等导致的不对称力矩都会对控制配平能力造成影响。图6给出了1#、2#发动机不同推力损失比例Rp下,不同故障发生时刻tF,发动机单独控制上升段配平能力分析结果。 图5 正常飞行有动力上升段状态曲线Fig.5 Flight curve for norminal ascent trajectory 图6 推力损失下发动机单独控制配平结果Fig.6 Trim results of engine control for loss of thrust 由图6可以看出,在单台发动机推力损失比例Rp在60%以下时,不同故障时刻均能够实现配平。随着推力损失比例的增加,摆动发动机产生的控制力矩减小程度增大,由推力损失引起的不对称力矩也逐渐增大,若推力损失60%以上时,会出现不可配平情况,且不可配平情况与故障发生时间有关,故障发生在约50~80 s之间时,配平能力下降最为严重。由图5可知该时间段为最大动压飞行段,机体气动力矩随动压增加,故推力损失故障下配平能力下降较为明显,而低动压区推力损失对配平能力的影响则不太显著。单台发动机故障关机是单台发动机推力损失的特例,即推力损失比例为100%的情况。由图6可以看出,单台发动机故障关机下所有故障时刻均不能配平,这主要是因为单台发动机关机情况下只剩2个控制量,无法控制3个通道飞行,故不能配平。 由图6(a)和图6(b)比较看出,故障发动机不同,其配平能力也不相同。主要是由于不同发动机故障下,推力损失产生的不对称力矩的方向与机体气动力矩的方向相同或相反造成的。1#发动机推力损失会产生正的偏航不对称力矩,相反2#发动机故障偏航不对称力矩为负。而在60 s附近机体偏航气动力矩基本为正。因此,2#发动机故障产生的不对称力矩刚好可以抵消掉一部分机体偏航气动力矩,而1#发动机产生的不对称力矩则进一步增加了需要的控制力矩,故在图6 中60 s附近2#发动机推力损失下配平能力明显强于1#发动机故障情况。 单台发动机推力损失故障下,配平能力不足时,需采用发动机/气动舵复合控制方式,配平结果如图7所示。可以看出,由于引入气动舵面进行控制,控制冗余度增加,故障下配平能力较图6明显改善,大部分故障时刻均能够实现配平。但在推力损失较大且故障发生在约90 s以后时,配平能力仍显不足。究其原因,是由于90 s以后,飞行高度较高,动压较低,气动舵效有所降低,没有足够的能力产生期望的力矩。 图7 推力损失下复合控制配平结果Fig.7 Trim results of combined control for loss of thrust 在复合控制也不能配平的情况下,必须采取相应的应急策略保证飞行的安全。一种解决方法是通过调节健康发动机的节流阀值来减小单侧发动机故障引起的不对称力矩,从而减小故障对控制系统的影响。分析表明,将健康发动机推力调小10%时,即可将图7中不可配平状态消除。 3) 发动机摆动喷管卡死情况 由图8(a)可以看出,对于喷管摆角δ1卡死情况,任意卡死角度下都不能够配平。这是由于2台发动机水平布置情况下摆角δ1和δ2用于同时控制俯仰和滚转通道,在δ1卡死某一角度时,剩余的一个控制量δ2无法保证同时满足俯仰、滚转2个通道的控制需求,必然会造成不同故障时刻均不能配平。 图8 摆动喷管卡死发动机单独控制配平结果Fig.8 Trim results of engine control for stuck nozzle 3.3 整个空域内配平能力分析 整个空域内配平能力分析是在给定的攻角α、马赫数Ma及飞行高度H范围内进行配平特性计算。定义所研究的飞行状态范围内能够配平的所有点的集合为可配平区域,不能配平的所有点的集合为不可配平区域。 在SRLV上升段飞行时,为了引入配平特性对飞行包络的影响,除了考虑一般的弯矩及动压等飞行约束外,还需要满足配平飞行约束。定义同时满足这3类飞行约束的所有点的集合为可飞区域。由于在(α,Ma,H)三维空间内研究可飞区域,在数据可视化及确定约束边界方面都不太直观,应寻求新的方法来描述可飞区域。考虑到每一组(Ma,H)都可计算得到对应的动压q,因此可飞区域还可描述为满足约束 (20) 的所有q-α空间内点的集合。这有利于确定考虑配平特性后的飞行约束边界及可视化的实现,具体方法在后面算例中有所体现。 1) 正常飞行情况 采用前面提出的方法,对无故障情况下上升段配平特性进行计算,分析配平特性对飞行约束的影响。结合现有上升段气动数据,选定在α∈[-10°,10°]、Ma∈[0.2,6]、H∈[0 km,60 km]范围内进行配平特性计算。 计算结果如图9所示。无故障下可配平区域占整个研究空域的84.76%。可以看出,若飞行高度H在约20 km以上时,可以实现配平,攻角和马赫数对配平能力影响不大。这是由于飞行高度较高时,大气密度快速衰减,使得飞行动压及气动力矩减小,因此配平能力较强。若飞行高度在约20 km以下,则大气密度较大,在亚声速段,气动力矩才不至于太大,因此可以配平;马赫数大于1时,不可配平区域与马赫数和攻角的大小均有关。 图9 无故障下三维不可配平区域Fig.9 3D nontrimmable region for norminal case 正常情况下上升段动压约束为q≤30 kPa,弯矩约束|qα|≤1 300 N/m2·rad,则结合配平分析结果可给出考虑配平能力约束后的可飞区域如图10所示。可以看出,无故障情况下只要满足动压和弯矩约束就能满足配平要求,配平性能对可飞区域没有影响,因此在轨迹设计或重构时不需要施加额外的配平能力约束。 2) 单台发动机推力损失情况 单台发动机推力损失故障对飞行约束的影响如图11及图12所示。1#发动机故障下,正攻角区域配平能力较差,结果表明推力损失程度在50%以下时,配平特性对动压、弯矩约束不会造成影响。2#发动机故障下,负攻角区域配平能力较差,结果表明推力损失程度在50%以下时,配平特性对动压、弯矩约束不会造成影响。 图10 无故障下配平能力对可飞区域的影响 Fig.10 Trim capacity effects on flyable region for norminal case 图11 1#发动机推力损失对飞行约束的影响Fig.11 Effects of loss of thrust of 1# engine on flight constraint 图12 2#发动机推力损失对飞行约束的影响Fig.12 Effects of loss of thrust of 2# engine on flight constraint 对于推力损失严重的情况,由于配平能力下降严重,导致可飞区域减小,除了动压约束和弯矩约束外,需要飞行中满足配平约束条件。如图11(b)、图12(b)所示,为了简化问题,配平能力约束边界建模采用直线形式,由q-α空间A、B点位置坐标(αA,qA)、(αB,qB)可将配平能力约束表示为 (21) 代入具体数据可得1#发动机推力损失70%时配平能力约束为 q≤-96 592α+28 446 (22) 2#发动机推力损失70%时配平能力约束为 q≤116 870α+21 000 (23) 3) 发动机摆动喷管卡死情况 摆角δ1卡死-10°故障下配平分析结果如图13 所示,若采用发动机单独控制则整个空域内都不能够配平,具体原因与与故障发生时刻配平分析相同。而采用复合控制后,故障对飞行约束的影响主要集中在气动舵效较低的低动压区,配平能力约束可近似表示为 q≥16 000 Pa (24) 图13 摆角δ1卡死-10°对飞行约束的影响Fig.13 Effects of δ1 stuck at -10° on flight constraint 1) 提出一种基于顶点投影法的相容性判定方法用于快速判定线性等式/不等式方程组解的存在性,并通过算例验证了方法的准确性与计算效率。该方法对于任意线性等式/不等式混合方程组具有普适性,程序实现简单,计算效率高。 2) 通过故障发生时刻配平能力分析,给出了亚轨道飞行器上升段发动机推力损失、摆动喷管卡死等故障模式下的不可配平区域,可为任务中止决策提供参考。同时就配平能力不足时的应急策略问题进行了探讨。 3) 通过整个空域内配平能力分析,给出了不同故障模式下,考虑配平能力约束下的可飞区域,并建立了简化的配平能力飞行约束数学模型,为后续故障后任务规划、轨迹重构及制导等研究工作提供依据。 4) 本文提出的方法也适用于无动力飞行段气动舵面故障情况下配平能力分析。 [1] GONZALEZ P. Influence of the abort capability in reusable systems reliabilit-FESTIP results overview: AIAA-1999-4928[R]. Reston: AIAA, 1999. [2] 李新国, 王文虎, 王晨曦. 亚轨道飞行器上升段故障模式分析与仿真[J]. 飞行力学, 2014, 32(3): 235-238. LI X G, WANG W H, WANG C X. Failure mode analysis and simulation of ascent trajectory for suborbital reusable launch vehicle[J]. Flight Dynamics, 2014, 32(3): 235-238 (in Chinese). [3] HANSON J M. A plan for advanced guidance and control technology for 2nd generation reusable launch vehicles: AIAA-2002-4557[R]. Reston: AIAA, 2002. [4] 陈永刚. 亚轨道飞行器控制系统设计[D]. 西安: 西北工业大学, 2008: 14-15. CHEN Y G. Control system design of the sub-orbital vehicle[D]. Xi’an: Northwestern Polytechnical University, 2008: 14-15 (in Chinese). [5] JACKSON M C, HU H. Autonomous ascent abort planning applied to military and civilian space launch vehicles: AIAA-2004-6586[R]. Reston: AIAA, 2004. [6] SHAFFER P J. Optimal trajectory reconfiguration and retargeting for the X-33 reusable launch vehicle[D]. Monterey, CA: Naval Postgraduate School, 2004: 21-25. [7] FAHROO F, DOMAN D. A direct method for approach and landing trajectory reshaping with failure effect estimation: AIAA-2004-4772[R]. Reston: AIAA, 2004. [8] SHAFFER P J, ROSS I M, OPPENHEIMER M W, et al. Optimal trajectory reconfiguration and retargeting for a reusable launch vehicle: AIAA-2005-6148[R]. Reston: AIAA, 2005. [9] SHAFFER P J, ROSS I M, OPPENHEIMER M W, et al. Fault-tolerant optimal trajectory generation for reusable launch vehicles[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(6):1794-1802. [10] 解永锋. 亚轨道飞行器应急返回与轨道重构技术研究[D]. 西安: 西北工业大学, 2011: 135-158. XIE Y F. Research on emergency return and trajectory reshaping of suborbital reusable launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2011: 135-158 (in Chinese). [11] 王娟, 刘小雄, 孙逊, 等. 基于优化配平的机翼故障飞机飞行性能分析[J]. 计算机工程与应用, 2014, 50(23): 229-233. WANG J, LIU X X, SUN X, et al. Flight performance analysis for aircraft with wing faults based on optimization of trimming[J]. Computer Engineering and Applications, 2014, 50(23): 229-233 (in Chinese). [12] PARADISE J A. Adaptable method of managing jets and aerosurfaces for aerospace vehicle control[J]. Journal of Guidance, Control and Dynamics, 1991, 14(1): 44-50. [13] JOHANSEN T A, FOSSEN T I, BERGE S P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J]. IEEE Transactions on Control Systems Technology, 2004, 12(1): 211-216. [14] 徐方暖. 亚轨道飞行器上升段虚拟样机设计[D]. 西安: 西北工业大学, 2008: 24-35. XU F N. Virtual prototype design of the ascent of suborbital launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2008: 24-35 (in Chinese). [15] 谭政. 亚轨道可重复使用运载器控制律研究[D]. 西安: 西北工业大学, 2009: 13-22. TAN Z. Research on flight control laws of suborbital reusable launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2009: 13-22 (in Chinese). [16] 宋恩民, 黄文奇. 判断具有多线性约束条件的凸空间是否为空的交边算法[J]. 计算机学报, 1996, 19(9): 704-708. SONG E M, HANG W Q. An intersecting-side algorithm to determine whether convex regions bounded by multiple constraints are empty[J]. Chinese Journal of Computers, 1996, 19(9): 704-708 (in Chinese). [17] 任世军, 洪炳熔, 梁庆姿. 判定线性不等式构成的凸集是否空集的位置算法[J]. 哈尔滨工业大学学报, 2000, 32(2): 121-124. REN S J, HONG B R, LIANG Q Z. A point positioning algorithm to determine whether convex regions bounded by multiple linear constraints are empty[J]. Journal of Harbin Institute of Technology, 2000, 32(2): 121-124 (in Chinese). [18] 任世军. 判定线性不等式围成的空间是否为空的梯度快速算法[J]. 哈尔滨工业大学学报, 2006, 38(9): 1441-1445. REN S J. Fast projection algorithm to determine the emptiness of regions bounded by linear constraints[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1441-1445 (in Chinese). Trimcapacityanalysisofsuborbitalreusablelaunchvehiclewithenginefailure WANGWenhu*,HANBing CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,China Inordertoanalyzethetrimcapacityofthesuborbitalreusablelaunchvehiclewithenginefailure,theproblemoftrimcapacityisconvertedtotheproblemofcompatibilitydecisionoflinearequality/inequalitymixtureequations.Amethodbasedonvertex-projectionisproposedandusedintrimcapacityanalysis.Theaccuracyandefficiencyofthemethodareverified.Intheframeworkoftrimcapacityanalysis,thetrimcapacitiesatfailure-timeandforstate-spaceunderdifferentfailuremodesareanalyzedrespectively.Moreover,contingencystrategyisgiveninthecasethattrimcapacityisinsufficient.Simulationresultsindicatethatthemethodcanrapidlycalculatenon-trimmableregion,andanalyzetheinfluenceoftrimcapacityonflyableregion.Theseresultshaveimportantreferencevaluesforabortstrategyandaborttrajectoryoptimization. suborbitalreusablelaunchvehicle;enginefailure;trimcapacity;compatibilitydecision;mixedequations 2015-12-28;Revised2016-05-27;Accepted2016-08-22;Publishedonline2016-08-261042 2015-12-28;退修日期2016-05-27;录用日期2016-08-22; < class="emphasis_bold">网络出版时间 时间:2016-08-261042 www.cnki.net/kcms/detail/11.1929.V.20160826.1042.004.html * .Tel.:0351-3557452E-mailwwhu@nuc.edu.cn 王文虎, 韩冰. 亚轨道飞行器发动机故障下配平能力分析J. 航空学报,2016,37(12):3646-3656.WANGWH,HANB.TrimcapacityanalysisofsuborbitalreusablelaunchvehiclewithenginefailureJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3646-3656. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0240 V448.1 A 1000-6893(2016)12-3646-11 王文虎男, 博士, 讲师。主要研究方向: 飞行器动力学与控制。Tel.: 0351-3557452E-mail: wwhu@nuc.edu.cn 韩冰男, 博士, 讲师。主要研究方向: 飞行动力学建模与仿真。Tel.: 0351-3557452E-mail: chihb2008@live.cn URL:www.cnki.net/kcms/detail/11.1929.V.20160826.1042.004.html *Correspondingauthor.Tel.:0351-3557452E-mailwwhu@nuc.edu.cn
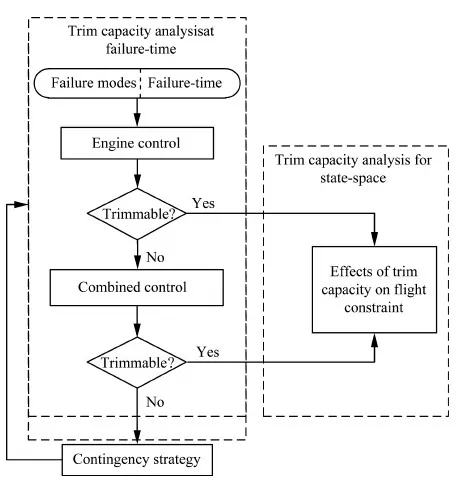
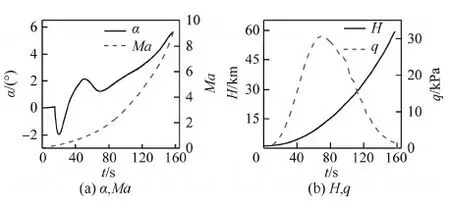
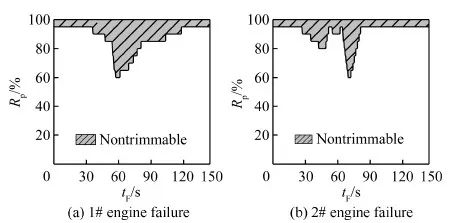
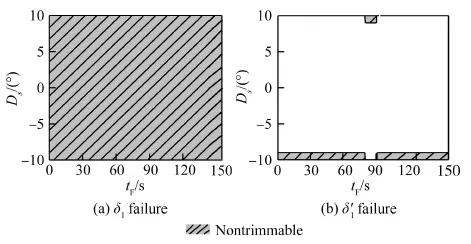
3 SRLV发动机故障下配平能力分析








4 结 论

