激光光斑中心高精度定位算法研究

陈和， 杨志浩， 郭磐， 张寅超， 陈思颖

(北京理工大学 光电学院， 北京 100081)



激光光斑中心高精度定位算法研究

陈和， 杨志浩， 郭磐， 张寅超， 陈思颖

(北京理工大学 光电学院， 北京 100081)

为提高测风激光雷达系统光学结构能量接收效率，需要对激光雷达系统中的激光光斑中心进行准确定位. 通过对常用亚像素定位算法的分析，利用高斯拟合和矩形区域来对灰度重心定位算法进行优化，提出了激光光斑定位的改进算法，并与已有的算法进行了对比分析，设计并开展了验证试验. 试验结果表明改进算法比已有传统算法对激光光斑的定位准确性大幅提高，最大限度地减小光斑形状的不对称所导致的误差，对于光能量分布中心的估计也更为准确，是一种切实可行的光斑中心定位算法.

相干测风激光雷达；激光光斑中心；高斯拟合-局部重心法；同轴性检测

对于相干测风激光雷达系统，为了获得回波信号的最大接收效率，需要保证耦合镜光轴与大气回波光轴尽量重合. 相干测风激光雷达系统的大气回波信号与望远镜镜面微量反射光光斑同光轴，因此可通过检测能量较强的镜面反射光光斑位置间接测量微弱大气回波信号光轴与耦合镜光轴的同轴性. 基于这一思路，一种值得研究的光轴检测方法如图1所示.

在测量回波信号光轴与耦合镜光轴的同轴性时，将图1中反射镜插入光路，由面阵探测器获取望远镜镜面微量反射光光斑图像，再利用光斑中心定位算法计算出中心位置的像素坐标. 将这一位置与光纤耦合镜光轴对应的像素位置基准进行比对，即可得到光轴偏差量，进而通过预设的调整镜进行微调节，使大气激光回波光轴与耦合镜光轴重合. 整个检测-调整过程可以实现闭环自动控制，而其中激光光斑中心的精确定位是保证光轴调整精度的一个重要前提[1].

1 常用算法原理介绍

目前，比较常用的光斑中心定位算法有灰度重心法[2-3]、二维高斯拟合法[4-5]、空间矩方法[6]等. 灰度重心法算法简单且测量精度高，能够达到0.2～0.5像素，但是它要求光斑形状比较规则，否则会产生较大误差；二维高斯拟合法定位稳定性较好，标准差能够达到0.1像素以下，测量精度能够达到0.1～0.3像素，但其测量精度易受图像的具体分布和采样数据样本大小影响，在实际处理中往往需要对图像和数据样本大小进行具体分析. 空间矩方法的精度高度依赖于光斑边缘，但光学系统像差等因素的影响使其受限于实际应用. 本文主要介绍灰度重心法和高斯拟合法.

1.1 高斯拟合算法

对于多数激光光束，其光强分布可近似为高斯分布. 取其高斯函数为

(1)

式中：T0为峰值参数；σx、σy为横向分布参数. 对式(1)两端取对数，展开平方项后可以得到

(2)

对于图像中适用于高斯拟合的区域，利用最小二乘法原理(残差平方和最小)进行高斯拟合，将拟合的极值点(x0，y0)作为光斑的中心位置[5].

1.2 灰度重心法

灰度重心算法的实现过程如下：假设面阵CCD的像素分辨率为m×n，并且光斑的图像灰度可表示为f(x，y)，其中x=l，2，…，m，y=1，2， …，n. 光斑重心实际上就是计算光斑图像的一阶矩，其坐标可以表示为

(3)

式中(xc，yc)为目标图像f(x，y)的形心.

2 高斯拟合-局部重心法

以上两种算法在实际应用中的局限性表现在：对于形状不对称的光斑，重心法精度会大大降低[7]；高斯拟合法的精度则受限于激光的实际光强分布. 本文结合重心法对对称目标定位精度高以及高斯拟合法稳定性好的优点，设计了一种高斯拟合-局部重心法(以下简称拟合重心法)，以期同时获得较高的定位精度与稳定度，并降低对光斑对称性和近高斯分布的依赖.

拟合重心算法的实现过程如下：设拟合的高斯函数为G(x，y)，将用于高斯拟合的N个数据点组成的方程组写成矩阵形式为

(4)

式中：B为N×1向量，元素为bi=lnGi，i=1，2，…，N；A为N×5矩阵，其中第i行是

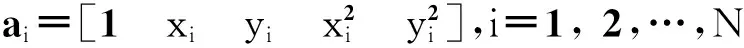
C为待求的高斯函数参数组成的向量

(5)

式中：xt，yt为高斯函数的极值点；c0为一常量；c1、c2则为高斯函数的横向分布参数.

设残差向量E=AC-B，用最小二乘法拟合，使其N个数据点的均方误差达到最小，引入最小二乘函数

(6)

并利用QR分解求出高斯拟合函数的极值点(xt，yt)，取最接近xt、yt的整数值作为矩形区域的中心点(xint，yint)，将该点灰度值记为I0. 然后在点(xint，yint)的周围，找到灰度值高于0.4I0的像素分布范围的外接矩形区域. 在这一矩形区域内，利用式(3)求出局部重心坐标，即作为算法输出的光斑中心.

3 算法实验验证

3.1 算法评价指标的选取

光斑中心定位算法的常用评价指标为稳定性与位移分辨精度. 稳定性是在光斑稳定时，进行多次测量，再对多次测量结果的标准差进行比较分析. 精度的评价是先使光斑在图像中产生确定的位移，然后评估算法计算出的光斑中心位移量与理论平移量μ的符合关系，利用标准差公式

(7)

计算n次测量的标准差.

由于以上两种指标对算法准确性的评估区分度较差，本文引入了以能够耦合进入光纤耦合镜的能量最大作为评价准确度的指标：在图像中确定与耦合镜孔径相对应的半径，以算法得到的中心为圆心，计算光斑在圆内的灰度值总和. 在图像量化未饱和时，圆内灰度值之和正比于孔径内的总光能.

3.2 实验系统与流程设计

用于算法验证的实验系统如图2所示，主要由激光器、扩束镜、CCD相机及一维高精度电控平移台组成. 其中激光器波长为532 nm，CCD分辨率为640×480像素，像元大小为5.6 μm×5.6 μm，灰度量化等级为8位. 实际实验中，由于激光光斑直径为6 mm，超出了CCD的成像尺寸，需要将扩束镜倒置使用，以缩小激光光斑光束直径，光斑图像的采集则由计算机控制自动完成. 实验过程如下：

① 调整所有器件到同一光轴，使得激光光斑位于CCD像面适当位置. CCD相机固定于一维高精度电控平移台上，平移方向与光轴垂直；

② 保持系统稳定，以120帧/s的速度采集多幅图像，由于激光器为连续工作激光器，即激光以连续方式持续输出，光斑图像可以在一段较长的时间范围内保持稳定，因此可以随机选取连续20幅图像分别对拟合重心法、灰度重心法和高斯拟合法进行稳定性与准确性的指标对比；

③ 控制电控平移台以固定的步长在水平方向平移，则CCD也随之移动，每平移1次拍摄1幅图像，连续平移5次，分别用拟合重心法、灰度重心法和高斯拟合法计算光斑中心位置的平移量，评估算法的可靠性；

④ 改变电控平移台的水平平移量，重复步骤③，然后对两次的平移量分别做对照实验.

CCD探测器中不可避免的噪声主要有热噪声和散粒噪声两种，为了减少噪声的影响，对采集到的光斑图像(图3)进行高斯滤波平滑处理，然后利用拟合重心法、重心法和高斯拟合法计算光斑中心位置.

3.3 稳定性实验结果

实验中第②步采集到的20幅图像为高帧频连续采集获得的，因此理论上光斑中心位置应该保持不变，标准差接近于0，图4(a)、4(b)为利用拟合重心法(fitting-centroid method)、重心法和高斯拟合法得到的光斑中心处理结果.

利用样本标准差公式计算这3种算法检测结果的标准差：高斯拟合法σx=0.034，σy=0.025；重心法σx=0.092，σy=0.202；拟合重心法σx=0.006，σy=0.005. 可以看到，拟合重心法得到的数据结果相对更加稳定，优于高斯拟合法和重心法.

3.4 准确性实验结果

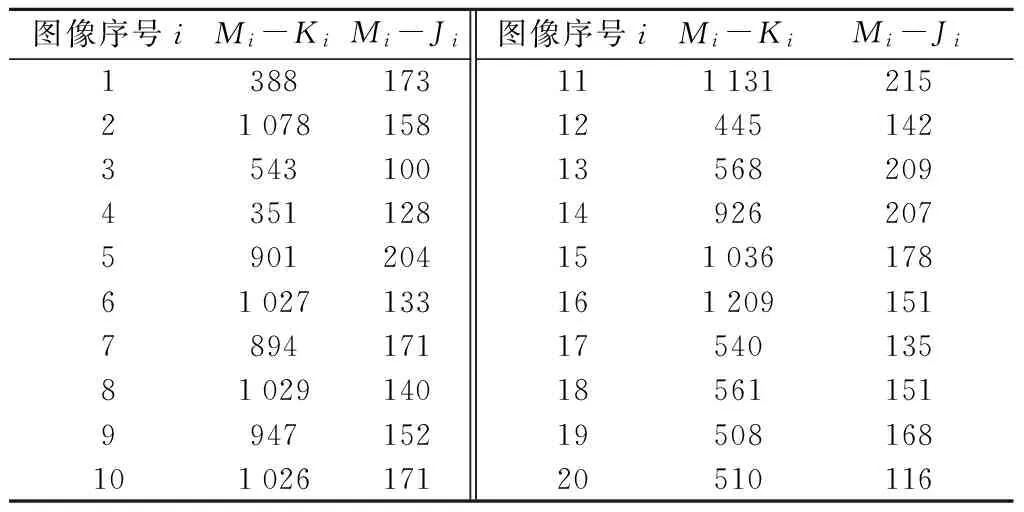
以实验中第②步以不同算法得到的光斑中心为圆心，取30像素为半径来匹配耦合镜孔径，分别计算不同算法得到的圆内所含像素灰度值总和并计算其差值，表1为实际处理结果(i表示图像序号，Mi、Ki、Ji分别为拟合重心法、重心法、高斯拟合法第i幅图像圆内光强).

从处理结果来看，本文算法得到的光斑中心为圆心的孔径内所包含的灰度值总和最大，优于高斯拟合法和重心法.

表1 3种算法的圆内灰度和之差

Tab.1 The difference between the total gray value of circle by three algorithms

图像序号iMi-KiMi-Ji图像序号iMi-KiMi-Ji13881731111312152107815812445142354310013568209435112814926207590120415103617861027133161209151789417117540135810291401856115199471521950816810102617120510116

3.5 位移精度实验结果

实验中CCD固定在电动平移台上以固定步长(5.3 μm)在水平方向上连续移动5次，因此，理论上这5个位置光斑中心(x方向)应该等间隔，光斑中心值(y方向)应该相同. 表2给出了各种算法对5.3 μm平移量的检测处理结果.

表2 中心平移量检测结果(5.3 μm)

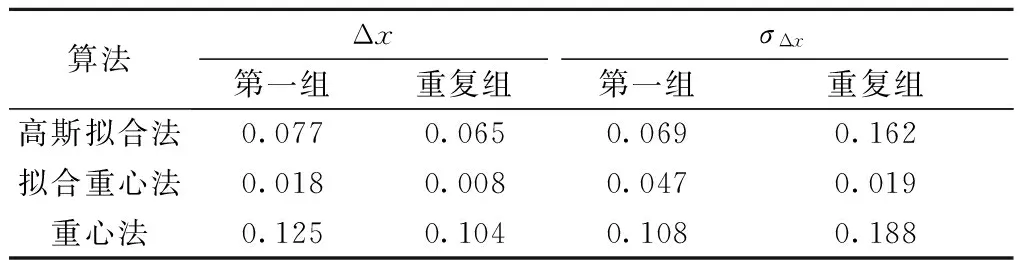
表3给出了平移量标准差的处理结果，其中σx为利用样本标准差公式计算得到算法平移量的标准差；σΔx为利用式(7)计算得到的与理论平移量(μ)0.946像素的标准差.

从表3中可以看出，本文算法对平移量的测量更为稳定，其精度小于0.05像素，并且优于高斯拟合法和重心法.

实验中电动平移台上以固定步长(27.8 μm)在水平方向上连续移动5次，表4给出了各种算法对27.8 μm平移量的检测处理结果.

表3 平移量标准差检测结果(5.3 μm)

Tab.3 The standard deviation results of displacement test(5.3 μm)

算法ΔxσΔx第一组重复组第一组重复组高斯拟合法0.0770.0650.0690.162拟合重心法0.0180.0080.0470.019重心法0.1250.1040.1080.188

表4 中心平移量检测结果(27.8 μm)

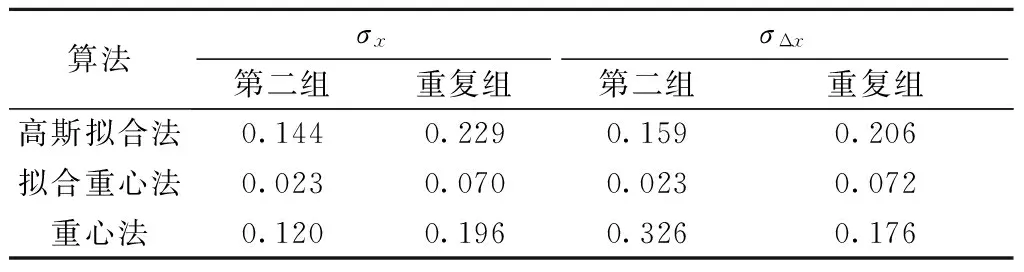
表5给出了平移量标准差的处理结果，其中σx为利用样本标准差公式计算得到算法平移量的标准差；σΔx为利用式(7)计算得到的与理论平移量(μ)4.96像素的标准差.

从表5中可以看出，本文算法对平移量的测量更为稳定，其精度小于0.1像素，并且优于高斯拟合法和重心法.

表5 平移量标准差检测结果(27.8 μm)

Tab.5 The standard deviation results of displacement test(27.8 μm)

算法σxσΔx第二组重复组第二组重复组高斯拟合法0.1440.2290.1590.206拟合重心法0.0230.0700.0230.072重心法0.1200.1960.3260.176

4 结 论

针对相干测风激光雷达系统的同轴性检测需要对激光光斑中心进行精确定位的要求，本文利用高斯拟合法提出一种拟合重心法(高斯拟合-局部重心法)，在光斑中心像素级精度的位置处选取最优的矩形区域，利用重心法计算光斑中心，最大限度地减小光斑形状的不对称所导致的精度误差，并用实际激光光斑进行验证分析. 实验结果表明该算法的稳定性高、标准差小；对微小位移测量精度达到了0.05像素，优于重心法和高斯拟合法；对于光能量分布中心的估计也更为准确，是一种切实可行的光斑中心定位算法.

[1] 骆新新，刘秉琦，孙东平，等.基于CCD的激光测距机光轴平行性检测[J].半导体光电，2009，30(3):460-463.

Luo Xinxin， Liu Binqi， Sun Dongping， et al. Based on the CCD laser range finder optical axis parallelism detection[J]. Semiconductor Optoelectronic， 2009，30(3):460-463. (in Chinese)

[2] 钱锋，贾建军，张亮，等.捕获、跟踪、瞄准系统中光斑探测相机的定位精度[J].中国激光，2013(2):176-182．

Qian Feng， Jia Jianjun， Zhang Liang， et al. Positioning accuracy of spot-detecting camera in acquisition，tracking， pointing system[J]. Chinese Journal of Lasers， 2013(2):176-182. (in Chinese)

[3] 尚学军，何明一，王军良.基于线阵CCD的光斑定位算法研究[J].激光与红外，2008，38(7):730-731．

Shang Xuejun， He Mingyi， Wang Junliang.Research of method in light-spot location based on linear CCD[J]. Laser & Infrared， 2008，38(7):730-731.(in Chinese)

[4] 李为民，俞巧云，胡红专，等.光点定位中的曲面拟合迭代算法[J].光学技术，2004，30(1):33-35．

Li Weimin， Yu Qiaoyun， Hu Hongzhuan， et al. Iteration algorithm of surface fitting in the detection of light-spot position[J]. Optical Technology， 2004，30(1):33-35.(in Chinese)

[5] 王丽丽，胡中文，季杭馨.基于高斯拟合的激光光斑中心定位算法[J].应用光学，2012，33(5):985-990．

Wang Lili， Hu Zhongwen， Ji Hangxin. Laser spot center positioning algorithm based on Gaussian fitting[J]. Applied Optics， 2012，33(5):985-990.(in Chinese)

[6] 郑毅.基于空间矩的激光光斑中心亚像素定位[J].激光与红外，2005，35(7):521-523．

Zheng Yi. Sub-pixel location of the center of laser spot based on spatial moments[J]. Laser & Infrared， 2005，35(7):521-523.(in Chinese)

[7] 徐亚明，邢诚，刘冠兰，等.几种激光光斑中心检测方法的比较[J].海洋测绘，2007，27(2):74-76．

Xu Yaming，Xing Cheng， Liu Guanlan， et al. The comparison of several kinds of laser spot center detecting method[J]. Hydrographic Surveying and Charting， 2007，27(2):74-76.(in Chinese)

(责任编辑：李兵)

Research of the High Precision Laser Spot Center Location Algorithm

CHEN He， YANG Zhi-hao， GUO Pan， ZHANG Yin-chao， CHEN Si-ying

(1.School of Optoelectronic Engineering， Beijing Institute of Technology， Beijing 100081, China)

In order to increase the receiving efficiency of the Lidar wind measurement system， it is necessary to locate the laser spot center with high precision. Based on the analysis of commonly used algorithm， the centroid method was improved by using Gaussian fitting and a rectangular region. Having analyzed and compared the new algorithm with the existing algorithm， finally the averification system was designed and the experiment was carried out. Experimental results indicate that the standard deviation and positioning precision of the new algorithm is both superior to those of Gaussian fitting and centroid method， in addition， the new algorithm can minimize the error caused by asymmetrical spot shape.The comparison results of the accuracy of light energy distribution center show that the new algorithm is also better than Gaussian fitting method and centroid method， which proved the new algorithm is a feasible method for laser spot center location.

coherent Doppler wind lidar;laser spot center; centroid method based on Gaussian fitting; detection of coaxality

2014-09-26

国家自然科学基金资助项目(61178072)

陈和(1982—)，男，博士，讲师，E-mail:shinianshao@gmail.com.

TN 247

A

1001-0645(2016)02-0181-05

10.15918/j.tbit1001-0645.2016.02.014