基于ANSYS W orkbench的齿轮齿条系统模态分析

马海龙

（秦皇岛天业通联重工科技有限公司，河北秦皇岛　066000）

基于ANSYS W orkbench的齿轮齿条系统模态分析

马海龙

（秦皇岛天业通联重工科技有限公司，河北秦皇岛066000）

齿轮齿条传动模态分析研究的主要内容是确定齿轮齿条部件的振动特性（固有频率和主振型），它们是承受动载荷结构设计中的重要参数。由于系统的固有特性表明了在哪些频率下结构会产生共振以及在各阶频率下结构的相对变形，因此对于改善结构动态特性具有重要意义。由模态分析就可判断出齿轮的转速是否合理，这样可以确定齿轮与齿轮转速合理匹配，进而避开其固有频率。

齿轮齿条模态分析ANSYS W orkbench共振

1　引言

模态分析是用来分析、确定系统振动特性的一种动力学分析技术。振动特性包括固有频率、振型等。在进行结构设计时可以利用模态分析避免共振，还可以为其他动力学分析模块提供求解控制参数，如时间步长等。在准备进行其他动力学问题之前首先要进行模态分析，模态分析是最基础的内容。

2　模态分析基本概念和理论

模态的定义是结构在进行自由振动时所具有的振动特性。结构本身的物理几何特性和材料属性决定着自身的模态，结构模态与外部是否添加载荷无关。进行模态分析时可以有两种方法：（1）理论模态分析，它的基础是线性振动理论。主要方法是利用有限元方法对所研究的结构进行离散，建立数学模型，求解系统特征值和特征向量，即求得系统的固有频率和固有振型。（2）实验模态分析，又叫模态分析的实验过程。首先，利用实验测得结构的激励和响应时间，运用数字处理技术求得频响应函数。然后运用参数识别方法得到系统结构模态参数。

运用弹性力学有限元方法可以得到齿轮系统的运动微分方程：

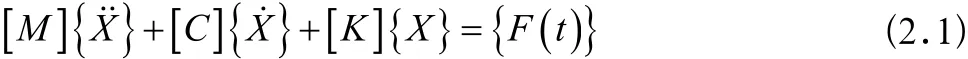
一系列简谐振动迭加为结构的自由振动，所以可以假设式（2.2）的解的形为：

将式（2.3）带入式（2.2）并消除因子ejωt，即得到求解特征值和特征向量问题的基本方程：

其中，［K］=刚度矩阵；

｛Φi｝=第i阶模态的振型向量（特征向量）；

ωi==第i阶模态的固有频率（ωi2是特征值）；

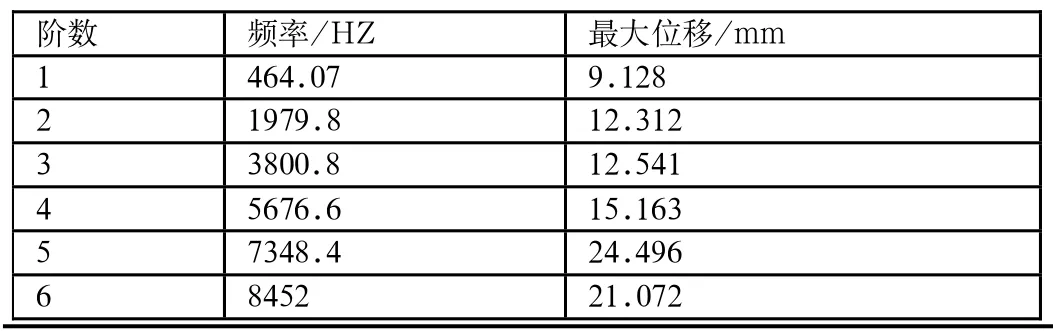
表1　齿轮齿条前6阶固有频率

［M］=质量矩阵。

上式有解的条件是：

式（2.5）称为结构的特征方程，通过求解该特征方程可以解得n个特征值ω12,ω22,···,ωn2，以及对应每个特征值的n个线性无关的n维特征列向量｛Φ1｝,｛Φ2｝,···,｛Φn｝。

3　齿轮齿条系统模态分析有限元建模

3.1齿轮齿条有限元模型的建立及材料的定义

利用UG软件建立三维模型以后，以x_t格式导入到ANSYS Workbench12.0中，得到在ansys中的齿轮齿条装配模型。在Geometry菜单中给齿轮齿条进行切片，为下面的局部网格划分打下基础。对模型的材料进行定义，在Engineering Data菜单中添加新材料，齿轮齿条采用的材料选用40Cr，40Cr作为为中碳合金结构钢，经调质并高频表面淬火后，可制作要求较高的表面硬度及耐磨性并带有一定冲击的零件，如齿轮、轴、连杆等。

3.2划分网格

由于计算机硬件条件的限制，本文对齿轮齿条进行切片，进行局部网格划分，细化网格可以使结果更精确，但是会增加计算机的运算时间，因此要权衡计算成本和细化网格之间的矛盾。而采用切片的方式进行局部网格划分这样可以减少网格划分数量，在载荷变化梯度较大的部位（如接触区域），为了较好地反映接触结果变化规律，需要采用比较密集的网格划分。

大大提高计算机的运算效率，网格划分采用自由划分。在齿轮啮合区域elem en t size设置为1mm，其他不重要的区域设置为20mm，得到31418个单元，154405个节点。

3.3加载约束

对齿轮齿条进行模态分析的目的是求出齿轮齿条各阶固有频率及其对应主振型。因此不需要对模型加载，只需对其进行自由度约束。为了达到与实际工况相符，必须保证齿轮只能绕Z轴旋转，齿条沿X方向平移。这就需要在Connections中对齿轮添加一个Revolute-ground约束，对齿条前表面添加一个Translational-ground约束。并在Modal中给齿轮添加Cy lindrical support（圆柱面约束），在齿条下表面添加一个Disp lacement（全位移约束），根据齿条的实际工况，给齿条在X，Y，Z方向添加强制位移，输入“0”代表此方向上已被约束，不设定某个方向的值则意味着齿条在这个方向上自由运动。

3.4定义接触对

根据模态分析的理论，在进行模态分析的时候，与刚度矩阵和约束有关系，约束不同则计算出来的刚度矩阵不同，固有频率也就不同。齿轮齿条啮合传动时轮齿之间是相互接触的，也就是说齿轮齿条之间有一种接触约束关系，所以在进行模态分析的时候它们之间的接触要加上。

4　齿轮齿条模态分析求解与分析

通过前面的有限元模型的建立以及约束的添加，进入M echanical后，程序设定的模态数是1～200，默认值是6。确定频率范围为0Hz～1e+08Hz，在本次分析中这样的设置能够达到要求，无需修改。

对结构进行模态分析时，一般不必求出全部固有频率和振型，而应着重考虑系统工作条件下所涉及的频率，一般只需计算较低的几阶频率，因为高阶振型对结构的动力特性影响很小。所以，通常只有这些低阶次的固有频率可能引起系统共振，如果有任何一阶的频率和其他机构的相同或是很接近，就可能发生共振。通过分析后处理器的前6阶固有频率，如表1所示，与其对应的振型图如图1所示。

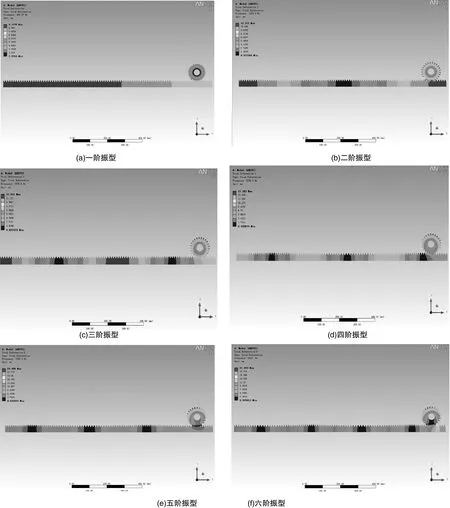
图1　齿轮齿条前6　阶固有振型

由模态分析结果知齿轮齿条最低模态频率464.07HZ。根据第一节由ADSMS得出的啮合激励频率为16HZ，远小于齿轮齿条最低固有频率，能够避开共振频率。

5　结语

为了提高生产效率，可以改变主推速度，从而可以得到不同生产效率下的外部激励条件。由模态分析得出的最低模态频率为464. 07HZ，即使在最高生产效率条件下，外部激励频率也远小于最低模态频率，没有落在固有频率范围之内，所以可以得出吸音板生产线在不同生产效率运行的情况下，主推系统能够避开共振频率，系统不会发生共振。

［1］成大先，王德夫，等.机械设计手册［M］.化学工业出版社.

［2］朱孝录.齿轮传动设计手册［M］.化学工业出版社.

马海龙（1988—），男，河北唐山人，工程师，秦皇岛天业通联重工科技有限公司，研究方向：起重机械。