例谈等差数列两个前n项和公式

安徽省蚌埠市怀远县第三中学　年四云

例谈等差数列两个前n项和公式

安徽省蚌埠市怀远县第三中学年四云

本文从思想方法的角度给出了等差数列前n项和两个公式在实际问题中的应用。

思想方法；等差数列前n项和公式

我们知道，教材就等差数列前n项和给出了两个公式：设等差数列的前n项和公式和为Sn，公差为d，n∈N＊，则（公式一），（公式二）。这两个公式在解决问题时如何使用，下面举例说明。以下m，n，p，q∈N＊，不再说明。

一、侧重于函数方程思想的公式一

1.方程思想

所谓方程思想就是将题目条件运用前n项和公式，表示成关于首项a1和公差d的两个方程，通过解决方程来解决问题。

解析：方程的思想，将题目条件运用前n项和公式，表示成关于首项a1和公差d的两个方程。

拓展：观察结构特点，将公式一做如下变形：

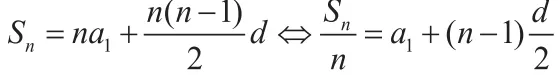
2.函数思想

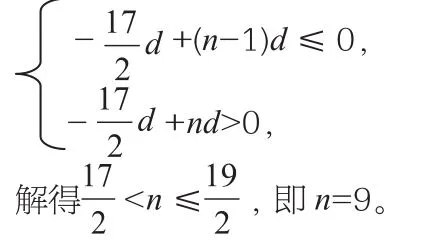
所以，此数列的前9项之和最小。

由此可知，当n=9时，Sn最小。

解法三：已知S5=S13，而Sn是n的二次函数（二次项系数＞0），由抛物线的对称性可得其对称轴方程为。所以，当n=9时，Sn最小。

点评：以上分别利用了单调性、配方转化为二次函数以及数形结合等，让学生比较以上这三种常见的解法，体会函数思想的作用。解法三做法中几乎没有运算，抓住了题目条件，结合数列的函数特性做处理，显得十分巧妙。

二、侧重于等差数列性质的公式二

1.侧重于性质：若m+n=p+q则am+an=ap+aq。

有些涉及等差数列前项n和的题目，常与等差数列的上述性质融合在一起，将a1+an与其他条件进行转换。

例题4 一个只有有限项的等差数列，它的前5项的和为34，最后5项的和为146，所有项的和为234，则它的第七项等于（）

A.22B.21C.19D.18

解：设该数列有n项且首项为a1，末项为an，公差为d，则依题意有

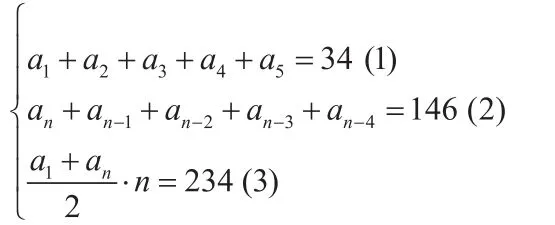
（1）+（2）结合上述性质可得a1+an=36，代入（3）有n=13从而有a1+a13=36，

点评：依题意能列出3个方程，若将a1+an作为一个整体，问题即可迎刃而解。在求a7时，巧用等差中项的性质也值得关注。知识的灵活应用，来源于对知识系统的深刻理解。

2.侧重于等差中项

利用等差中项，可以实施等差数列前n项和Sn与其通项an的转换：

点评：利用等差中项建立起等差数列前项和与其通项的联系是解决本题的关键。