生态元素：为数学学习设计智慧的锦囊

江苏省张家港市合兴小学　李春娟

生态元素：为数学学习设计智慧的锦囊

江苏省张家港市合兴小学李春娟

数学是一种文化。数学学习是用“发现”和“创造”并举实现文化传承的，具有生态表现力。切入生态元素，链接起以背景、标记、成果、线索、主题、价值的数学知识资源库，建构起以集合、交合、磨合、复合、融合、契合的学习方式能源系，为预期的学习结果提供一个智慧的锦囊，促进学习过程中个性化的数学思考和共性化的经验在场的和谐，摆脱对抗、纠结、消解，走向平和、认同、共识的达成度。

生态元素；数学学习；预期；学习结果；智慧

数学教学的目标是预期的学生数学学习结果。数学学习是用“发现”和“创造”并举实现文化传承的，因此，数学学习的生态表现力非常突出。生态元素，帮助学生基于一次次预期的学习结果形成数学思考的立场，实现提升智慧的视角。在实际的研究中，如何切入生态元素，促进学生的数学学习，打开智慧的锦囊呢？下面我结合自己的教学研究实例，谈谈自己的一些做法和思考。

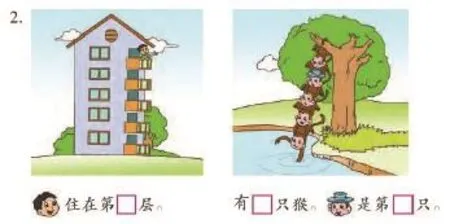
一、选择背景，前提与结果集合生态元素

计算、证明、推理是数学学习的三大重要能力。推理导向前提与结果的关系是学生思维能力的重要和关键环节。一年级的数学学习倾向于生活认识经验逐步发展成数学思维活动经验，在生活化和数学化之间，选择背景，表达出前提与结果，集合生态元素是主要任务。例如，认识几和第几是一年级上册认数安排的教学内容，对于是几的认识、表示事物的多少、基数的含义，学生平时接触很多；但是对于第几、表示事物的位置、序数的含义，还是需要建立观察和判断的秩序，如从上往下，还是从下往上，还有左右、前后的角度，所以这一部分内容是需要学生自己既可以符合生活习惯做出一个判断，也可以根据实际情况自主去选择顺序观察做出多样化的结果。教材上小猴捞月的故事中，如下右图所示，戴帽子的小猴就是一个特例，实现问题的背景的陈述意义是很重要的。在课堂上，多数学生填写的结果是第4只，少数学生填写的是第2只。为什么结果不一样？我把这个问题给学生了，学生自己去发现自己的观察角度和别人的想法不一样，体会到结果表示的意义不一样。在这里，我指出了选择观察的顺序再确定排列的位置需要认真想一想，明确顺序了才能确定排列的位置。数学学习的一个意义，定量刻画和定性描述的结合，这里真是很好地体现了。数学表达的根据，条理性，前提和结果的关系，有怎样的前提，也就是问题的背景来决定着思考的结果，这里不能矛盾。很好地把数学的说理、分析、判断、推理推向一个深刻的层次。低年级的数学问题情境具有童话故事色彩，同时也具有挑战性的激励。数学是简单的，数学又是不简单的。让学生的思维从已有的经验中组织起数学知识，可比性，数学化，呈现知识的建构过程，也凸显思维发展经历的过程，看数学、懂数学、用数学、玩数学、学数学，让学生在课堂上成为一个伟大的发现者，创造者。

二、赋予标记，形式与内容交合生态元素

数学是人类文化的重要组成部分，它以自己特有的表征、符号化来不断地丰富自己的内涵，同时又在不断地扩大外延。在直观和抽象之间，赋予标记，表达出形式与内容，交合生态元素是必经环节。例如，0的认识教学安排在认识1到5后，教材通过童话情境引入0的认识，接着通过多角度来认识，0还可以表示起点、表示分界点、表示编码、表示状态。0在生活中丰富的表现性突出了对于学生需要组织自己已有的认知经验。教材呈现的素材并不陌生，学生都有感性接触，对0的认识研究，就是依靠数学教学来达到对数学化的建构，同时完成自然数从无到有的一个认识序列的建立。我作了思考和预设，对于0的外形的样子，学生在书写时感到有困难，这是因为他们的观察空间和把握能力还是需要指导的，因此在书写时加强对比，学生就容易发现范例的书写和自己书写的不同，修改自己的起笔、运笔、收笔的过程。儿童的注意力、可比性就在于观察深入，修正自己的观察角度。为什么用一个空的符号表示？我想要是结合原来数的表示，用方框或者空着，后来人类发现就用圆圈表示，然后完善成现在的书写样子。这样的话，让学生理解起来，一个也没有可以用0来表示，再衍生出其他的作用，那么从数学知识的符号化历史上渗透数学文化教育，也让学生知道数学原来是创造赋予完善变化的过程。

三、规范成果，发展与补充磨合生态元素

荷兰数学教育家弗赖登塔尔认为，数学学习是不断地横向化和纵向化，这就意味着指向知识的广度和思维的深度上，过程与结果之间，规范成果，表达出发展与补充，磨合生态元素是指示策略。例如，加法是一年级上册的教学内容，对于加法运算的结果，是怎样算的，学生第一次需要自主去探索和建构，在课堂上，学生出现的状况是；为什么3+2等于5？有一个学生的思考是3往后再数2个就得到5了，我肯定了她的想法，同时让学生在图中观察，原来用数一数计数的方法是可以得到结果5的，说的很好。谁还有补充或新的想法？这时课堂上举的小手多了，一个学生说3和2合成5，用分与合的知识就知道了。我及时肯定了他的想法，也是多数小朋友的想法，原来我们学习的数学知识是有联系的，前面分与合的知识就是帮助我们更好地学习加法，计算结果的。熟记分与合，就会使学习变得简单和容易了。第一个学生的发言的确有道理，进入到20以内的加法的计算，凑十法，就是建立在数的基础上，方便容易观察出结果，所以要凑十，这和数一数的计数，在原来的基础上往后推出几得到几，一点也不矛盾，用序数的意义来建构这种算法也是正确的。用分与合的知识，利用基数的含义来建构也是正确的。这里是统一的，也是殊途同归，第一次算法的多样化，也让我看到儿童的数学活动经验，可以直观数一数，推算结果，推向思维一个同化动态过程，可以抽象合一合，解释结果，推向思维一个顺应平衡的过程。两者都是把数的抽象意义、表示的基数和序数的含义充分发挥出了重要的意义。建构意义，思维的生长，印证一次数学思考的发展与突破提升的创造力。

四、切换线索，顺应与推进复合生态元素

数学学习是一个帮助学生完善认知结构的过程，实现逻辑意义—潜在意义—心理意义的过程。潜在意义更多的是让知识的交接点能够在逻辑性联动和可能性发展之间，切换线索，表达出顺应与推进，复合生态元素是核心动力。例如，20以内的进位加法9加几是第一课时的教学内容，作为计算教学，算法的探索应该是学生必须经历的过程，在出示问题后，组织学生展开讨论交流是怎样算出一共有13个。课堂上的意见有看着图数过去，9到10，就是11、12、13，用数一数，序数表示的个数对应基数个数，就得到13了；还有的就把其中的1个青苹果搬到盒子里，变成了一盒，是10个，外面是3个了，就得到13个了。学生基于自己的理解，都在变魔术。哦，都在变魔术，都先变到了几10。就变到13了。很了不起的劲儿，还能想个好办法变魔术呢！只要拿出1个青苹果到盒子里，就变成10，就得到是十几了。你会变一变吗？试一试。学生都能按照要求变出10，得到是十几了。挑战成功。那为什么一定要先变出10呢？因为是9加4，9加7，先找到10，就容易得到十几了。把这样创造的方法叫作凑十法。凑十是个好办法，一眼就能得到十几？简单方便准确。那你是怎么凑十的呢？要先把9加的数，分出1和几。为什么要先分出1呢？因为9和1合成10。看来9加几，只要先把几分一分，分成1和几。先和9凑成十，十和分出的几合成十几就行了。要变出一个10，怎么变的？从算理到方法，建构过程中选择、判断、分析、综合处理。涉及分与合的知识，数的组成意义知识的提取，思维敞亮在课堂里，魔术的神奇的力量，数学的创造力量。

五、跟进主题，平衡与调整融合生态元素

数学思维最基本的两大方面是精确的定量化方法和严密的逻辑推理。数学是关于模式的科学，可见直觉洞察和验证把握之间，跟进主题，表达出平衡与调整，融合生态元素是行动措施。例如，认识100以内的数时安排的思考题，课堂上通过多媒体演示，两个笔筒里16支的笔，分成8支和8支，就同样多了，而27支演示到最后还没结束，学生就大声说，多1支，把最后的1支放在一个笔筒后，另一个笔筒就少，马上说27是单数，不能使分得同样多。还有一个小朋友说要是3个笔筒，每个笔筒里就9支，就能同样多了。不难发现，学生的思维状态发展到的程度，光是发现单数不能分成同样多的两份还不够，还发现可以再调整，可以分成3份，每份同样多，要使分得的同样多改变分的份数，可见思维又处于另一个状态的连接，可行的办法让学生从小就有一个思考问题的多面处理手段的发现。在这里，我想表达儿童学习的思维经验，当他们用于一个问题的解决时，是会自己调整，他们的想法是丰富的，只是那些丰富在现实和数学知识之间需要嫁接起一种认识，这种认识包括观察、体验、活动、联想、打破、立新。就上面的单数不能等分成两份，双数能等分两份，后来我又带学生验证去观察体验一下。找一找身边的数，伸出小手，打开手臂，一共有几根手指？10根，每只手是5根，10是双数，分成2份，它能分成同样多，看来能说明双数能分成同样多的两份。耳朵、眼睛呢？也能，学生点头，这样还保证我们对称漂亮，我补充提示，那嘴呢，鼻子呢？大家都笑了，不能。我们是在自己身上就能找数学知识，带着愉快和轻松，下课了，学习数学真不失为审美的创造！

六、回归价值，实践与应用契合生态元素

数学教育始终坚持生活之眼、生长之理、生命之气，让学生亲历感受、涵泳体悟，窥见本真情趣、理性崇高壮美。荷兰数学教育家弗赖登塔尔认为，只要儿童没对自己的活动进行反思，他就达不到高一级的层次。让数学回归生活吧！课内和课外之间，回归价值，表达出实践与应用，契合生态元素是智慧诉求。如：我们认识的数是教材安排综合与实践活动，课堂内，抓一把豆子数一数，估一估，数一数时，我主要提出了发现什么，学生知道抓一把，物体的个儿有大小，所以个儿大的数量少，个儿小的数量多，特别是数绿豆的孩子，一把绿豆很多，数也来不及数，数的时候也要小心，要不要数错的。正是通过辨析个儿的大小，就可以推想数量的多少。这里的数学可以表达为对一种常识的梳理，也是把观察和认知的经验用数学的形式化来表达，看成一个关系的建立，即同样抓一把，物体的形状的大小决定它的多少，也是数和形的关系，是制约关系。课堂外，教材提出最后“你还能数出校园里哪些物体的个数？”如下图所示，适合学生的实践能力的培育，在课堂上我带学生出去了，并提出了要求，完成的任务，是需要自己记下五种物体的名称，不会写的字用拼音代替，然后记下数出的个数。排着长长的队伍，出发经过图书馆大楼、教学楼、办公楼、回到乒乓台前，一路数，有花坛、灯笼、树、亭子、乒乓桌、灯杆，就是小黄杨数不清，桂花树还可以数清，一路上看、数、记，走走停停，回到教室里后，开心交流，有的是一样，有的不一样。经过这样的发现，写生，自己去经历了活动，开放的数学，去生活看一看，走一走。在实践的过程中，学生感受到数学研究的是存在与对应，联系与区别，整体与部分，对立与转化，事理与数理，会想与会用，写照灵动和清远的智慧。

综上所述，生态元素主要关注预期的数学学习结果基于数学思考的立场上进而提升智慧的视角。链接起以背景、标记、成果、线索、主题、价值的数学知识资源库，建构起以集合、交合、磨合、复合、融合、契合的学习方式能源系，为预期的学习结果提供一个智慧的锦囊，促进学习过程中个性化的数学思考和共性化的经验在场的和谐，摆脱对抗、纠结、消解走向平和、认同、共识的达成度。

［1］郑毓信，梁贯成.认知科学、建构主义与数学教育［M］.上海：上海教育出版社，2002.

［2］史宁中.数学课程标准解读（2011年版）［M］.北京：北京师范大学出版社，2012.

［3］（美）拉尔夫·泰勒著；罗康，张阅译.课程与教学的基本原理［M］.北京：中国轻工业出版社，2014.

［4］喻平.数学教学心理学［M］.北京：北京师范大学出版社，2010.

［5］曹才翰，章建跃.数学教育心理学［M］.北京：北京师范大学出版社，2006.

［6］（荷兰）弗赖登塔尔著；陈昌平，唐瑞芬等编译.作为教育任务的数学［M］.上海：上海教育出版社，1995.