基于信号集合势和连续性的认知无线电宽带频谱感知

申 滨,喻 俊,黄 琼,陈前斌

(重庆邮电大学移动通信技术重点实验室,重庆 400065)



基于信号集合势和连续性的认知无线电宽带频谱感知

申 滨,喻 俊,黄 琼,陈前斌

(重庆邮电大学移动通信技术重点实验室,重庆 400065)

针对传统感知算法依赖主用户信号与噪声先验信息,以及易受噪声功率估计不确定性影响的缺点,提出了一种基于信号集合势和连续性的宽带频谱感知方案.该方案将宽带频谱感知分为主用户占子带集合势的估计和子带位置判决两步.在两次不同感知结果中利用主用户连续占用子带的特性,有效地实现最终感知性能的提升.理论分析和仿真结果表明,该方案不仅能够解决传统感知方法依赖噪声和主用户信号先验信息的问题,而且对抗噪声功率不确定性具有鲁棒性.特别地,与传统的能量检测频谱感知算法相比,该算法能有效地实现宽带频谱盲感知.

认知无线电;宽带频谱感知;集合势估计;能量检测;谱函数

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.032

1 引言

认知无线电(Cognitive Radio,CR)[1，2]因其能够动态地利用时空上空闲的授权频谱,被认为是未来实现动态频谱接入、解决频谱资源匮乏问题的关键技术.在CR研究的诸多技术中,CR频谱感知是其核心技术之一,是实现频谱管理、频谱共享等技术的前提.

近年来,CR宽带频谱感知因其能够灵活地监控宽带频谱上的可用空闲频段而受到广泛关注.当前,关于宽带感知的研究主要分为:(1)信道化的宽带感知;(2)非信道化宽带感知.信道化的宽带感知是将宽带频谱分为单个授权频带(Licensed Frequency Band,LFB),然后对其进行感知判决,例如,滤波器组[3]、信道化能量检测器[4].非信道化宽带感知则并未对子带划分,直接进行宽带感知判决.例如,宽带压缩感知[5].以上宽带感知存在的主要问题有:(1)若不进行信道化的划分,则在PU占用带宽比例较小的情况下,感知结果易受累计噪声的影响并且无法提高宽带上的可用频谱分辨率;(2)在信道化的宽带感知中,若采用串行感知,则效率太低.为了克服以上矛盾,文献[6]中探讨了多信道LFB联合检测,提出了一种基于多频带联合检测的宽带感知方法.但是,总的来说,这些研究或多或少地需要关于PU和噪声的先验信息,因而在普遍意义上缺乏灵活度和鲁棒性.文献[7]中探讨了信息论准则(Information Theory Criterion,ITC)在宽带频谱感知中的应用,以ITC来估计被授权用户(Primary User,PU)占用子带的个数,能一定程度地解决这些不足,但其检测性能受信噪比(Signal Noise Ratio,SNR)和采样数影响较大,难以满足CR宽带感知的实际应用要求.

当前,对ITC的研究仍受到广泛关注[8～11].例如,利用线性收缩估计噪声子空间方式[8],利用特征值的分布等改进ITC中条件概率密度函数[9,10],利用特征值升幂的方式[11]等.这些方法大多只从某一方面对ITC的性能进行提升,并不能就一致性、稳定性、复杂度、检测能力等性能达到全面的提升.

为了解决上述问题,本文基于集合势的概念,将整个宽带感知分为被PU占用子带集合势的估计和子带位置的判决,利用估计出的集合势代替原有能量检测(Energy Detect,ED)[12]算法中的门限,解决了对先验信息的依赖性和对抗噪声不确定性缺乏鲁棒性的问题.

2 宽带系统感知模型

由图1可知,宽带频谱感知实则是从子带构成全集中确定被PU占用子带子集SPU;而子集SPU的确定,主要包括子集SPU中元素的个数M的确定(即集合势的确定),以及这M个元素的具体值(即子带位置的确定).

在频域中,宽带LFB上子带的忙闲与否采用二元假设表示,使用Ηq,0表示第q个子带被占用状态,Ηq,1表示其空闲状态.在感知时间Ts内,第q个子带的第n次快拍信号rq(n)为:

(1)

3 集合势的估计

确定集合SPU的关键在于其势的确定,在众多方法中,基于协方差矩阵[13]的方案提供了一种对先验信息依赖程度低的估计方法.假设感知时间Ts内,SU接收机快拍N次得到感知数据协方差矩阵C:

C=E[r(n)rH(n)]

=HE[s(n)sH(n)]HH+E[v(n)vH(n)]

=HCsHH+Cv

(3)

其中,r(n)=[r1(n),r2(n)…rQ(n)]T,s(n)=[s1(n),s2(n),…,sQ(n)]T,v(n)=[v1(n),v2(n)…vQ(n)]T.Cs为PU信号协方差矩阵,H=diag[h1,h2,…,hQ]为信道增益矩阵,Cv为噪声协方差矩阵,I为Q阶单位矩阵.

理论上,协方差矩阵C一般通过下式计算:

(4)

3.1 集合势估计之基本准则

为了解决以上问题,ITC中的Akaike信息准则(Akaike’s Information Criterion,AIC)和最小描述长度(Minimum Description Length,MDL)已被用于宽带频谱感知中集合SPU势M的估计[8],其表达式如下所示,由对数项和补偿项两部分组成:

(5)

由于AIC并不满足一致性,MDL受SNR影响较大,文献[15]提出了一种基于二者加权的WIC准则,而在实际应用中,WIC的性能介于AIC和MDL之间,较之二者提升很少,特别是在宽带感知中,难以满足低SNR下的集合势估计的要求.因此,本文提出一种指数嵌入族准则(Exponentially Embedded Families,EEF)[16,17]用于估计集合SPU的势M,能有效地解决以上问题,更符合宽带感知要求.该准则表达式为:

(6)

这里,u(·)表示单位阶跃函数,LM(r)表示似然比函数,其定义为:

(7)

根据矩阵特征值分解理论,有:

(8)

将参数的ML估计值代入各准则的表达式,经数学运算及化简,可得到:

(9)

(10)

其中Ω=α+β+γ,而

(11a)

(11b)

(11c)

根据ITC、EEF准则估计势M的方程为:

(12)

(13)

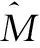
在频谱感知中,微弱信号的检测是核心难题.在低SNR下,ITC和EEF准则都会产生很大的M值的低估,导致最终检测率过低.文献[11]中通过对MDL低估的原因进行详细分析,认为提高其准确估计的方法大致可以分为两类:对特征值升幂或减小补偿项.

3.2 盖氏酉变换准则

矩阵CM经Gerschgorin酉变换后为ZM=VHCMV,将其估计值代入条件概率密度函数,经化简、取log等运算后代入式(5),省略常数项及无关项,可得Gerschgorin定理下的ITC集合势的估计[18]为:

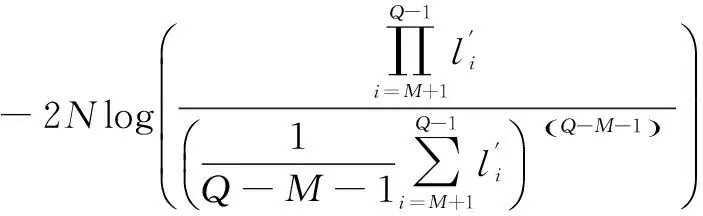
(14)

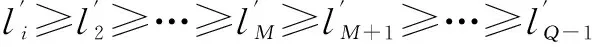
(15)

其中,φM≈M2,Ω′=α′+β′+γ′,而

(16a)

(16b)

(16c)

因而,GITC和GEEF估计势M的判决方程为:

(17)

(18)

从图2中可以看出:当采样数N从10000减到100(与矩阵维度Q相当)时,较小的特征值li几乎为0,而此时其几何平均/算数平均的比值几乎为0,在M=40时也不具有明显的变化,从而致使以上准则失效.

3.3 基于RMT的改进

为了解决特征值li波动较大对以上准则的影响,在RMT中,直接考虑噪声特征值li的分布情况.对于特征值li(i=M+1,M+2,…,Q),有[19]:

(19)

(20)

按照式(7)的定义,可求得log似然比函数LM(d),将LM(d)及φM=M+1代入式(6),可得

RMT下新的EEF判决准则为:

(21)

因而,经RMT改进后,RMT-ITC和RMT-EEF估计集合SPU的势M的估计方程为:

(22)

(23)

3.4 基于采样功率的改进

由图2可知,相对于特征值li而言,子带上N次采样的功率θq更加稳定,受采样数N影响较小,而且,当N→∞时,θi=li=λi(i=1,2,…,Q).因而,可考虑利用子带N次采样的功率值替代上式中的特征值li[8].

从图3((a)、(b)右图是对左边的部分放大)中可以看出:当采样数N从10000减到100(与矩阵维度Q相当)时,由于子带功率的波动较小,使得Χ<0恒成立,致使RMT系列准则失效.因此,通过比较可以看出,子带采样功率θq对于几何平均/算术平均这种结构更稳定,特征值对于平方的算术平均/算数平均这种结构更稳定.

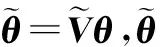
(24)

将上式代入ITC准则的似然函数中,简化及省略无关项[8],可得到基于采样功率的ITC准则为:

(25)

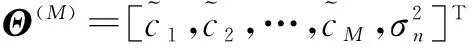
将式(24)代入EEF准则的似然比函数中,可得到基于采样功率的EEF准则为:

(26)

其中Ω″=α″+β″+γ″

(27a)

(27b)

(27c)

因而,基于SP的ITC和EEF估计M的方程为:

(28)

(29)

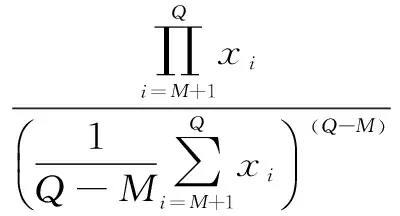
在算法实现中,相对于特征值分解(为O(Q3)量级,Q为矩阵维度)，其它操作的计算量较小,因而,表1中算法SP-ITC(SP-EEF)的复杂度最低.由于GITC(GEEF)不仅需要进行特征值分解,并且还需要进行Gerschgorin酉变化等一系列操作,因此,相对来说其复杂度最高.RMT-ITC和ITC只涉及特征值的运算,因此,二者复杂度相当.但是,相对于RMT-ITC(RMT-EEF)而言,由于ITC(EEF)中涉及到几何平均数和对数运算,因此,ITC的复杂度略高于RMT-ITC.至于EEF系列与ITC系列算法相比,由于前者的计算结构更为复杂,因此复杂度相应地更高.

表1 各估计准则的比较

值得说明的是,集合势M的估计方法并不局限于文中所提及,还有许多其它的方法.例如,结合序列检测与假设检验的SHTE[21,22],Gerschgorin圆半径的迭代GDE[18]等.这些方法也大多是基于协方差矩阵进行的.

4 子带判决统计量

在整个盲感知过程中,SU所依赖的仅仅是N次采样数据,因此,子带上N次采样的功率成为一种最常见的判决统计量.在本文中,通过对SU接收到的采样数据的分析,提出了一种关于特征值的判决统计量用于子带判决.

4.1 基于子带谱函数的判决

假设已知整个宽带授权频带上被PU占用的子带数为M,则式(1)中的信号模型也可以分解表示为[8]:

r(n)=Gx(n)+v(n)

(30)

其中,x(n)=[xq1(n),xq2(n),…,xqM(n),0,…,0]T,结合式(1)可知,xqm(n)=hqmsqm(n),x(n)为接收端吸收了信道系数的接收信号,qm(m=1,2,…,M)为M个子带在宽带LFB上的具体位置.Q×Q的变换矩阵G=[g1,g2,…,gM,…,gQ]为单位阵IQ经初等行变换后的矩阵,每行每列只有一个元素为1,其余都为0.

相应地,协方差矩阵C可表示为:

(31)

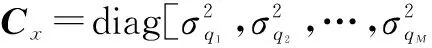
(32)

分析式(32),由Us与Uv间的正交性及Us为次酉矩阵,有:

(33)

(34)

其中,IM为M阶单位矩阵,em为第m个元素为1的M维单位向量.

由于gm为某一元素是1的单位向量,因而,可构造子带谱函数Ψv和Ψs为:

(35)

(36)

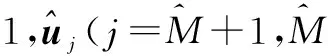
假设宽带频谱监测范围分为64个子带,连续被占子带的个数为20个,被占的子带范围为[15,34].图4、图5分别给出了每个子带上对应的采样功率和谱函数(图中的Ψw为加权谱函数)值随SNR、采样数N变化的示意图.

4.2 基于加权谱函数的判决

由图4、5可看出,受采样数N的限制,PU占用子带和空闲子带的谱值并不为理想值.而且随着SNR降低,被占子带的谱函数值(Ψv或Ψs)波动较大,与空闲子带之间的差距越来越不明显.因而,为了减小这种波动带来的误判,提升二者之间的辨识度,需要进一步对二者进行改进.

结合二者,可构造加权子带谱函数Ψw(q)为:

(37)

5 基于被占子带连续性的改进

由图1可知,在实际应用中,PU占用的子带往往不止一个,而是会占用整个LFB中的多个连续子带.

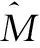
(38)

(39)

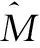
(40)

故

(41)

6 仿真结果及分析

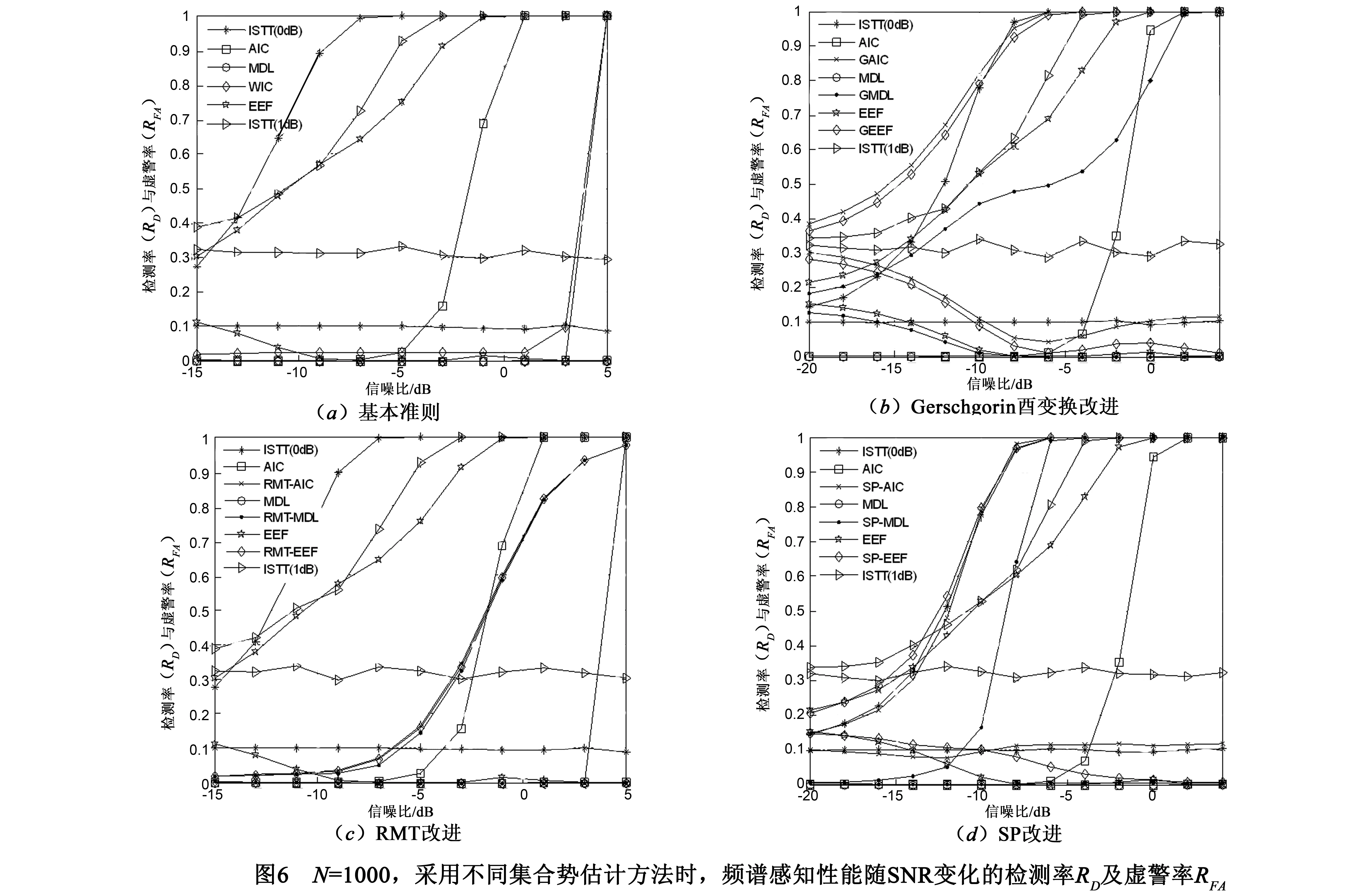
仿真1 采样数N=1000时,仿真不同集合势估计方法,依据功率值θq判决子带时的宽带频谱感知算法性能.从图6中看出,WIC算法的性能介于AIC与MDL之间,EEF算法性能较之ITC有很大的提升,但与ISTT(α=0)仍然相差很远.经改进后,盖氏系列、SP系列的性能都有很大的提升,但是RMT系列的性却与AIC相当,仍离ISTT(α=0)仍有不少差距.GAIC与GEEF,SP-AIC与SP-EEF,RMT系列的性能较为接近,其中GAIC和SP-AIC并未表现出一致性,SNR较高时,其RFA也不为0.低SNR时,GAIC比SP-AIC(及GEEF比SP-EEF)的RD高,而GAIC(GEEF)的RFA也相对较高.

仿真2 仿真采样数N=100,不同集合势估计改进方法,依据功率值θq判决子带时的宽带频谱感知算法性能.从图7可以看出,ITC、EEF、GITC、GEEF估计算法失效,RMT-ITC、RMT-EEF、SP-ITC、SP-EEF估计算法性能较为稳定,但是受N影响,性能都有很大的削弱.与ISTT(α=0)相比,RMT系列性能相差很远,SP系列性能较为接近,且SP-EEF满足一致性.

仿真3N=1000时,仿真GEEF、SP-EEF估计算法,依据谱函数和功率值θq进行子带判决时的感知性能.从图8可知,依据Ψv(q)、Ψs(q)、Ψw(q)、θq判决的结果仅有细微的差别.而且,按照其顺序,感知性能依次略微增强.

仿真4 采样数N=1000时,分别仿真基于GAIC和GMDL估计集合势,谱函数判决子带,以及基于SP-AIC和SP-EEF估计集合势,功率θq判决子带的子带连续性(SC)改进算法性能.在图9中,SC改进感知算法利用被占子带的连续性,从高RFA判决集合中剔除了部分空闲子带,往低RD判决集合中吸收了部分被占子带,很好的提升了整个感知方案的性能.

7 结束语

本文提出了一种基于信号集合势和连续性的宽带频谱感知方案.在不依赖先验信息的条件下,将频谱感知过程分为被占子带集合势的估计和子带状态的判决两步来实现.仿真结果表明,该方案不仅能够解决传统宽带感知算法对抗噪声功率不确定度的鲁棒性较差的缺陷问题,而且可进一步提高有限时间段内的有限次快拍条件下的感知性能,因而可作为宽带频谱感知的可实现方案.

[1]Haykin S.Cognitive radio:brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.

[2]王钦辉,叶保留,田宇,等.认知无线电网络中频谱分配算法[J].电子学报,2012,40(1):147-154.Wang Qinhui,Ye Baoliu,Tian Yu,et,al.Survey on spectrum allocation algorithms for cognitive radio networks[J].Acta Electronica Sinica.2012,40(1):147-154.(in Chinese)

[3]Aliasgari M,Birjandtalab J,Fakhraie S M,et al.Deep out-of-band radiation reduction by using joint filterbank and cancellation carriers in cognitive radios[A].Telecommunications (IST),2012 Sixth International Symposium on[C].IEEE,2012.271-276.

[4]Lehtomaki J J,Juntti M.Detection of frequency hopping signals using a sweeping channelized radiometer[J].Signal Processing,2005,85(10):2030-2043.

[5]Ariananda D D,Leus G.Compressive wideband power spectrum estimation[J].IEEE Transactions on Signal Processing,2012,60(9):4775-4789.

[6]Quan Z,Cui S,Sayed A H,et al.Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J].IEEE Transactions on Signal Processing,2009,57(3):1128-1140.

[7]Liu S,Shen J,Zhang R,et al.Information theoretic criterion-based spectrum sensing for cognitive radio[J].IET Communications,2008,2(6):753-762.

[8]Huang L,So H C.Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J].IEEE Transactions on Signal Processing,2013,61(9):4806-4821.

[9]Yazdian E,Gazor S,Bastani H.Source enumeration in large arrays using moments of eigenvalues and relatively few samples[J].IET Signal Process,2012,6(7):689-696.

[10]Lu Z H,Zoubir A Z.Generalized bayesian information criterion for source enumeration in array processing[J].IEEE Transactions on,Signal Processing,2013,61(6):1470-1480.

[11]Lu Z H,Zoubir A Z.Flexible detection criterion for source enumeration in array processing[J].IEEE Transactions on Signal Processing,2013,61(6):1303-1314.

[12]Zhang S B,Dong X D,Bao Z H,et al.Adaptive spectrum sensing algorithm in cognitive ultra-wideband systems[J].Wireless Personal Communications,2013,68(3):789-810.

[13]Zeng Y H,Liang Y C.Eigenvalue-based spectrum sensing algorithms for cognitive radio[J].IEEE Transactions on Communications,2009,57(6):1784-1793.

[14]Schmidt R O,Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Instrumentation and Measurement,1986,34(3):276-280.

[15]Chen P,Wu T J,Yang J.A comparative study of model selection criteria for the number of signals[J].IET Radar Sonar Navigation,2008,2(3):180-188.

[16]Kay S.Exponentially Embedded Families-New approaches to model order estimation[J].IEEE Transactions on Aerosp & Electron & Syst,2005,41(1):333-344.

[17]Xu C C,Kay S.Source enumeration via the EEF criterion[J].IEEE Lett on Signal Processing,2008,15:569-572.

[18]Qing H,Liu Y,Xie G.Robust spectrum sensing for blind multiband detection in cognitive radio systems:a gerschgorin likelihood approach[J].KSII Transactions on Internet & Information Systems,2013,7(5):1131-1145.

[19]Nadakuditi R R,Edelman A.Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples[J].IEEE Transactions on Signal Processing,2008,56(7):2625-2638.

[20]Abd-Krim Seghouane,Maïza Bekara.A small sample model selection criterion based on kullback’s symmetric divergence[J].IEEE Transactions on Signal Processing,2004,52(12):3314-3323.

[21]Xiao M L,Wei P,Tai H M.Estimation of the number of sources ased on hypothesis testing[J].Journal of Communications and Networks,2012,14(5):481-486.

[22]Xiao M L,Lu J Q,Wei P.An estimator of the number of sources based on a sequence of hypothesis test[A].2011 International Conference on Computational Problem-Solving (ICCP)[C].IEEE,2011.538-543.

[23]Tandra R,Sahai A.SNR walls for signal detection[J].IEEE Journal of Selected Topics in Signal Processing,2008,2(1):4-17.

申 滨 男,1978年生于贵州兴义,博士,重庆邮电大学教授.研究方向为认知无线电、IR-UWB等.

E-mail:shenbin@cqupt.edu.cn

喻 俊 男,1987年生于湖北麻城,重庆邮电大学硕士生.研究方向为认知无线电频谱感知.

E-mail:yu-jun1988@qq.com

Signal Set Cardinality and Contiguity Based Wideband Spectrum Sensing for Cognitive Radio

SHEN Bin,YU Jun,HUANG Qiong,CHEN Qian-bin

(KeyLaboratoryofMobileCommunicationsTechnology,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China)

To solve the problem that traditional spectrum sensing methods require a prior knowledge of the noise power and the primary user signal,and are vulnerable to noise uncertainty,signal set cardinality and contiguity based wideband spectrum sensing schemes are proposed for cognitive radios.The proposed schemes perform wideband spectrum sensing in two phases:estimation of the cardinality of occupied subbands set and decisions of the occupied subband location.Through different cardinality estimations,performance can be effectively improved by exploiting occupied subbands continuity feature.Theoretical analysis and simulation results verify that the proposed algorithm demands no a prior knowledge of the noise power and the primary user signal,and is robust against the noise power uncertainty problem.It can effectively discern subbands status blindly,compared with the conventional spectrum sensing methods.

cognitive radio;wideband spectrum sensing;subspace identification;energy detection;spectrum function

2014-11-20;

2015-08-26；责任编辑：蓝红杰

国家自然科学基金(No.61201205，No.61379159);国家863高技术研究发展计划(No.2014AA01A701)重庆市自然科学基金(No.CSTC2012JJA40043)

TN929.5

A

0372-2112 (2016)08-1994-10