基于AFT满足下行约束的物理拓扑发现方法

张 宾,刁兴春,刘 艺,俞 赟,袁 震,丁晨路,蒋国权

(总参第63研究所,江苏南京 210007)



基于AFT满足下行约束的物理拓扑发现方法

张 宾,刁兴春,刘 艺,俞 赟,袁 震,丁晨路,蒋国权

(总参第63研究所,江苏南京 210007)

物理拓扑发现对于网络管理和应用具有重要意义,基于地址转发表的物理拓扑发现是目前学术界研究的热点问题.但由于实际网络的地址转发表通常不完整,导致了物理拓扑发现的难度,本文基于降低在实际拓扑发现时对AFT完整性的要求,定义了地址转发表的三类约束,并提出了地址转发表满足下行约束的树型剪裁算法,用于发现子网的物理拓扑结构.算法极大地降低了拓扑发现对地址转发表完整性的要求,是对仅通过下行端口地址转发表进行拓扑发现的最松约束.模拟仿真实验验证了算法的正确性和高效性,算法在实际网管系统中的部署进一步验证了算法在真实网络环境中的实用性.

物理拓扑发现;地址转发表;网络管理;

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.014

1 引言

网络拓扑发现分为逻辑(网络层、三层)与物理(链路层、二层)拓扑发现两种,逻辑拓扑发现是指发现路由器间及路由器和各个子网间的连接关系,而忽略子网内交换机与主机等设备的物理连接关系,物理拓扑发现是指发现管理域内交换机与主机及路由器等设备间的实际连接关系.

网络层的拓扑发现按发现的不同级别可以分为[1]:IP接口级、路由器级、PoP级、AS级,发现方法主要有:Ping方法、Traceroute方法、DNS方法、SNMP和ARP方法、路由协议方法、Tomography方法等.网络层拓扑发现技术研究的相对成熟,有很多项目和产品应用这些技术进行拓扑发现,比如惠普的Open View、IBM的Tivoli等,然而这些产品都依赖于私有协议,难以发现大型局域网中含有不同厂商交换设备的二层拓扑结构.许多网络管理任务,比如性能分析、网络规划和模拟、异常检测等都依赖于二层的拓扑发现,因此,准确实时的二层拓扑发现对于网络管理和应用具有重要的意义.

网络设备的地址转发表(Address Forwarding Table,AFT)记录了设备端口在一段时间内的实际通信的设备地址,基于地址转发表的物理拓扑发现是目前学术界研究的热点问题,也是物理拓扑发现的最重要方法.但通常实际网络的AFT不完整,导致了物理拓扑发现的困难,本文基于降低在实际拓扑发现时对AFT完整性的要求,定义了AFT的三类约束,并提出了AFT满足下行约束的树型剪裁算法,用于发现子网的AFT满足下行约束的物理拓扑结构,算法仅依赖于下行AFT,且不要求下行AFT完整,本文提出的算法极大地降低了对AFT完整性的要求,是对仅通过下行端口AFT进行拓扑发现的最松约束.

2 相关工作

二层的拓扑之所以难以发现的主要原因是:(1)大部分的拓扑发现工具主要用于发现网络层拓扑,要求管理员手工维护二层连接信息,而且MIB中并不直接提供网络节点间的直接链接信息;(2)二层设备的地址转发表包含了可达的地址信息,但信息通常不完整.

为了克服这些困难,IETF于2000年推出物理拓扑MIB[2],试图解决网络层以下拓扑结构的发现问题,但是由于没有确定如何获取这些MIB对象的机制而难以应用,为了弥补这种状况,IEEE提出链路层发现协议(LLDP)作为802.1AB-205标准的一部分,LLDP是一个厂商无关的二层协议,它允许网络设备在本地子网中通告自己的设备标识和性能.但是目前已部署的很多设备上并不支持这个协议.还有一种邻居发现协议CDP,而CDP是思科私有的协议,只能发现思科的二层设备.

除了可以应用邻居发现协议来直接发现二层设备的连接关系外,目前二层拓扑发现算法主要有基于生成树协议、基于地址转发表、基于端口流量特征及基于探测包的方法.

文献[3～5]将网络流量特征引入拓扑发现算法中,把网络设备接口的流量变化看作随机过程进行研究,尝试通过流量特征相近程度来推断网络的物理拓扑,但这些方法依赖于统计相关,只能大致推断出可能的链接,并不能确定设备间一定存在相应的连接,而且在不同子网间的设备互联时这种方法的正确性还有待验证.

文献[6]中提出一种基于生成树协议的方法,其基本思想是利用生成树的信息构建网桥设备之间的连接关系,该方法的优点在于时间和空间消耗较小,可以发现局域网中的备用链路,缺点是许多交换机不支持生成树协议,使其适用范围受到一定的限制,并且该方法不能发现交换机和主机之间的连接关系.

文献[7]中提出一种基于探测包的方法,其基本思想是,在每个主机上设置一个代理进程,产生一些探测包,并把网卡设置在混杂模式下(在该工作模式下,网卡可以接收到网段内的所有数据包),然后,根据每个主机所接收的数据包来判断设备之间的连接关系,该种方法可以判断出交换机之间、交换机和主机之间的连接关系,缺点是在每个主机设备上都要设置一个代理进程,这对一个较大型的网络来说是不太可能的事情.

总体来说,上述方法都具有较大的局限性,目前的二层拓扑发现的研究重点主要基于地址转发表,每台交换机都维护一张地址转发表,地址转发表的记录格式可以简单地表示为信息对,其中,port称为转发端口;MAC 称为转发地址.转发端口为p的转发条目构成一个子集,称为端口p的转发表.如果交换机端口p的地址转发表中包含了该端口所能接收到的所有数据帧的MAC 地址,则称该端口的地址转发表是完整的.

贝尔实验室的Breitbart等人提出了基于完整地址转发表的物理拓扑发现方法[8,9],可以发现跨子网交换域的拓扑结构,其算法的核心是直接连接定理:分属两个交换机的一对端口是相连的,当且仅当这两个端口的地址转发条目集合的交集为空,且其并集中包含了该子网中所有交换机的地址条目.Bejerano等人[10]进一步提出一种基于不同完整地址转发表的多子网拓扑发现算法,该方法首先根据地址转发表和子网信息构造出不同结点之间的粗略路径,然后进一步为每一条路径构造出一组路径约束,利用路径约束信息,不断细化粗略路径,最终确定一条唯一的路径.

基于完整地址转发表的方法存在一个难以克服的缺点,即需要保证地址转发表的完整性.为了做到这一点,Breitbart[8,9]提出增加额外流量和连续采集两种方法来提高地址转发表的完整性.郑海等人[11]通过在管理站上Ping所有交换机的方法来保证下行端口的地址转发表的完整性.在实际网络中,由于地址转发表老化机制的存在、地址转发表长度的限制以及SNMP协议采用无连接的UDP进行通信,不能提供可靠的数据传输,因此,交换机地址转发表的完整性很难保证,从而影响这些算法的准确性.

郑海等人[11]提出了一种方法,该方法仅要求只要下行端口的地址转发表是完整的,就可以构造出交换机之间的连接关系.陈福等[12]提出了一种新型的数据结构“树型图”,也仅要求下行端口的地址转发表完整即可构造出连接关系.Lowekamp等人[13]提出了一种更为宽松的基于非完整地址转发表的拓扑发现算法,算法要求一对交换机节点的AFT间至少共享三个转发条目,该算法把网络拓扑中的连接分为两种类型:直接连接和间接连接,该算法基于这样一个定理(间接连接定理):如果两个交换机仅有一对端口的通过集相交为空,则这对端口必然相连(间接连接).但这三种方法一个较大的缺点是只能适用于一个子网的拓扑发现,在交换域跨越多个子网时很容易出错.

孙延涛等[14]试图提出一个完备的规则,如果仅依赖地址转发表,两个交换机之间的端口连接是可以唯一确定的,则利用此规则,就可以唯一确定这两个端口的连接关系.在此规则的基础上,文中提出了一种有效的算法推导出交换式以太网的物理拓扑关系,但文中并没有对所提规则的完备性作证明.Bejerano[15,16]提出了一个很简单的方法来发现多子网局域网的拓扑结构,文中定义了一种Skeleton-Tree的数据结构,算法主要思想是用Skeleton-Tree自顶向下构建每个子网的拓扑结构,然后子网间合并出整个交换域的拓扑结构,这个算法能发现大部分的网络拓扑情况,但这个算法要求下行端口AFT完整且上行端口AFT中含有根节点的地址.

Gobjuka和Breitbart在他们的工作[17～22]中证明了AFT不完整时二层拓扑发现的NP难问题,并且给定AFT表是否能定义一个唯一的拓扑也是NP难问题;在给定AFT完整时,他们提出一种算法能发现所有可能的拓扑图并定义了拓扑唯一的条件;在给定AFT不完整时,他们提出了一组规则来扩展AFT并提出了三种算法满足不同情况需要,第一个是当所有节点的AFT中都含有同一个节点地址的情况,第二个是每个节点的AFT在半完全的情况,第三个是针对任意AFT情况但并不保证能发现正确的拓扑结构.

在对相关工作的阐述中我们可以看到,由于实际网络的AFT通常不完整导致了拓扑发现的困难,目前仅依赖下行端口AFT的拓扑发现方法是郑海等人[11]提出的,但他们的方法要求下行端口的AFT完整,这在实际网络中是很难满足的,基于这样的动机,本文提出了一个基于下行端口AFT的树型剪裁算法,本文提出的算法是对仅通过下行端口AFT进行拓扑发现的AFT完整性要求的最松约束.

3 下行约束算法

3.1 算法基础

由于交换域内的交换机必须遵循生成树协议,其它链路只作为备用链路而不参与实际的数据传输,因此,可以将交换域建模为一棵无向树G=(D,E),D是交换域内所有结点(网络设备)的集合,E是设备端口之间的直接连接集合,若S表示所有交换机的集合,H表示所有主机、路由器及一些哑设备(HUB、中继器等)的集合(二层拓扑发现可以将路由器作为主机处理),则D=S+H,每台交换机都维护一张地址转发表(AFT),若以Si表示交换域中第i台交换机,Sij表示Si的第j个接口,Aij表示端口Sij的地址转发表,如果Aij包含了Sij所能接收到的所有数据帧的MAC地址,则称Sij的地址转发表是完整的.在根交换机确定的情况下,我们称树型结构中交换机上连链路的端口为上行端口,显然上行端口是唯一的,交换机其它的端口称为下行端口.

如果一个交换域只包含一个子网,那么Aij就对应于网络中节点Si通过端口Sij在交换域生成树的路径中可能到达的节点集合,当AFT完整时,Aij含有了路径中所有节点的集合[8,9].但这对于交换域含有多个子网的情况并不成立,因此,一个多子网的交换域内即使所有端口的AFT完整也并一定能确定唯一的拓扑结构[8,9].如果我们假定网络中不含有度数为2的哑设备,这时,单子网交换域网络的AFT完整必定可以唯一确定这个网络的拓扑结构,因此,单子网交换域的生成树G有以下性质.

性质1 如果单子网交换域网络的AFT完整,这样的AFT必定可以唯一确定网络生成树G的拓扑结构.

证明 由于生成树G中任意一个节点Si的Aij完整,此时,Aij含有了端口Sij在交换域生成树的路径中所有可达节点的集合,这时,对于网络中的另外一个任意节点的端口Smn的地址转发表Amn与Aij只可能存在两种情况:(1)Amn≠Aij,两者不等时,则这两个端口的连接也必定不同,否则必然Amn=Aij;(2)Amn=Aij,即这两个端口的AFT完全相同,这时可以判定是存在一个哑设备连接这两个端口.因此,无论对于哪种情况,都可以唯一确定网络生成树的拓扑结构.

性质2 网络生成树G中节点的上行端口是唯一的.

这是树的基本性质.

除了性质2,树的其它性质也可以用于网络生成树G中,根据性质1,完整的AFT可以确定唯一正确的网络生成树的拓扑结构,因此,对于单子网交换域,我们可以定义如下三类约束:

定义1 最小约束AFT 如果通过子网的网络节点的AFT可以构造出唯一正确的子网拓扑结构,则称这样的AFT满足最小约束,即满足最小约束的AFT可以唯一确定子网的拓扑结构.

定义2 下行约束AFT 在根交换机确定的情况下,每个交换机的上行端口至少包含一个祖宗交换机地址(即不能为空),这时,如果仅通过交换机的下行端口的AFT就可以确定子网的唯一拓扑,则称AFT满足下行约束.

定义3 上行约束AFT 在根交换机确定的情况下,每个交换机的下行端口至少包含一个子孙节点的地址(即不能为空),这时,如果仅通过交换机的上行端口的AFT就可以确定子网的唯一拓扑,则称AFT满足上行约束.

显然,子网的完整的AFT是满足最小约束的,满足最小约束的AFT却并不一定是完整的,但满足最小约束的AFT和完整的AFT都可以唯一定义一个子网的拓扑结构,因此,总可以找到一些规则,使得满足最小约束的AFT经规则推导后成为完整的AFT;同理,对于上行端口确定时,下行约束AFT也可以通过一些规则得到下行完整的AFT;对于下行端口确定时,上行约束AFT也可以通过一些规则得到上行完整的AFT.从对这三个约束的定义可以知道,满足最小约束AFT是能通过AFT得到子网唯一正确拓扑结构的AFT不完整的最松约束,满足下行约束AFT是仅通过下行AFT得到子网唯一正确拓扑结构的下行端口AFT不完整的最松约束,满足上行约束AFT是仅通过上行AFT得到子网唯一正确拓扑结构的上行端口AFT不完整的最松约束.

虽然满足最小约束AFT是AFT不完整的最松约束,但显然研究通过满足最小约束AFT得到子网唯一正确拓扑结构的拓扑发现算法是最困难的,研究满足下行约束AFT和上行约束AFT算法相对要简单些,本文着眼于研究满足下行约束AFT的拓扑发现算法,上行约束和最小约束算法的研究会在我们的后续工作中逐步展开,同时这里也为其他学者提供了一个开放的研究课题.

对于满足下行约束的AFT,具有这样特征,树中每个节点的下行端口的AFT中或者含有其孩子节点的地址或含有孩子节点至少两个下行链路可达的节点的地址,如图1表示一条从树根到叶子的任意一条链路,Si和Sk表示链路中任意两个相邻节点,其中Si是Sk的父亲节点,以Bkt表示Sk下行端口t的可达地址,则Si的端口j的AFT或者含有Sk的地址,即Sk∈Aij,或者∃a∈Akl且∃b∈Akt,且{a,b}⊆Aij,因此,我们有定理1.

定理1 满足下行约束的AFT要求每个节点的下行端口的AFT中或者含有其孩子节点的地址或者含有孩子节点至少两个下行端口所连接的下行链路中节点的地址.

证明:图1中的父子节点Si和Sk不失一般性,若Sk∉Aij,且Aij只含有Sk一个下行端口(如端口l)的下行链路中节点的地址,则图1中节点Si和Sk的位置显然可以进行互换,互换后的拓扑结构并不影响任何节点的AFT,因此,不满足下行约束的AFT会导致链路中任意两个父子节点Si和Sk的顺序无法确定.

定理得证.

从定理1可以知道,如果节点中的孩子节点只有一个下行端口,则节点必含有孩子节点的地址.对于满足下行约束的子网的AFT,显然无向树G=(D,E)变成了下行有向树,每个父亲节点或者有指向其孩子节点的链接(也同时有可能有指向任意子孙的),或者有指向其孩子节点至少两个下行端口可达的子孙节点,这样我们就可以提出一个十分简单有效的树型剪裁算法,以O(n2)的算法复杂度来得到正确的拓扑结构,n为节点数.树型剪裁算法基于这样一个简单的思想,如果一棵树所有的分叉及其连接的叶子被砍掉,而砍掉的分叉变成一个新叶子,这样树就可以一层层被砍光.在介绍算法前,我们先给出四个定义.

定义4 叶交换机 交换机的所有下行端口都连接的是非交换机设备,称这样的交换机为叶交换机.

定义5 中间交换机 定义所有的非叶交换机为中间交换机.

定义6 叶端口 定义交换机连接叶交换机的端口为叶端口.

定义7 叶子 定义所有终端设备(如主机和路由器)为叶子节点.

叶交换机的下行端口可以连接主机、路由器、HUB等设备,显然中间交换机至少有两个端口连接其它交换机,由此,可以证明以下三个定理.

定理2 叶交换机只有一个端口的AFT含有其它交换机的地址.

证明:根据叶交换机的定义,叶交换机的下行端口不可能连接其它交换机,而树型结构中的上行端口只有一个,根据下行约束的定义,每个交换机的上行端口至少包含一个祖宗交换机地址(即不能为空),因此,叶交换机只有一个端口(上行端口)的AFT含有其它交换机的地址.

定理得证.

定理3 中间交换机要么至少有两个端口的AFT含有其它交换机的地址,要么一个端口的AFT含有其它交换机的地址并且至少存在一个端口含有的叶子节点地址分布在其它交换机的不同端口上.

证明:根据中间交换机的定义,它的上行端口的AFT必然含有一个祖宗交换机的地址,另外,它必然有一个下行端口存在孩子交换机,根据定理1,此下行端口要么含有其孩子交换机的地址,要么含有孩子节点至少两个下行端口所连接的下行链路中节点的地址.当此下行端口含有孩子交换机的地址或者含有孩子节点至少两个下行端口所连接的下行链路中节点的地址存在一个子孙交换机地址时,这时,这个中间交换机至少有两个端口的AFT含有其它交换机的地址;当此下行端口含有孩子节点至少两个下行端口所连接的下行链路中节点的地址都为叶子节点地址时,这时,由于叶子节点地址来自两个以上不同的下行链路,此下行端口含有的叶子节点地址必然分布在其它交换机的不同端口上,即一个端口(上行端口)的AFT含有其它交换机的地址并且至少存在一个端口(下行端口)含有的叶子节点地址分布在其它交换机的不同端口上.

定理得证.

定理4 如果叶交换机父亲的叶端口AFT含有交换机的地址,那么它只含下级叶交换机的地址而不含任何其它交换机地址.

证明:根据叶端口的定义,叶端口只连接的交换机为处于树型结构中的最下层的叶交换机,不连接任何中间交换机,因此叶端口AFT中的地址只可能含有其直接连接的叶交换机地址或叶交换机所连接的终端地址,而不可能含有其它交换机的地址.

定理得证.

3.2 树型剪裁算法

有以上的定义和定理作基础,这样,对于满足下行约束的AFT,我们提出的树型剪裁算法基本思想如下:

(1)设置交换机(含交换机地址和端口AFT)集合H.

(2)确定叶交换机Sk:找出Si中只有一个Aij含有其它交换机的地址的Si为叶交换机(根据是否在H中确定)的备选(定理2),再根据定理3剔除备选叶交换机中存在的中间交换机,把所有的叶交换机从H剪除,如果叶交换机某个下行端口出现多个叶子地址,表示有HUB等哑设备连接叶子.

(3)更新H中的AFT:把剩余Aij中地址为剪除掉的叶交换机下行端口含有的地址全部替换为叶交换机的地址Sk,并合并重复项,相当于把剪除的叶交换机变成了新的叶子节点,转入步骤(2),直到H只剩根节点.

下面我们论证树型剪裁算法的正确性.首先我们给定一个普适的真理,即:如果给定一颗树,每次砍掉它的最下层分叉(此分叉向下连接的所有节点均为叶子)及其连接的所有叶子,而砍掉的分叉用新的叶子替代,则这棵树最终会被砍剩下只剩一个根节点.我们提出的树型剪裁算法就基于这样的一个真理.步骤(1)相当于确定了树的所有节点的集合,其中终端节点即叶子节点为树的叶子,叶交换机为直接连接叶子的最下层分叉,中间交换机为其它分叉;步骤(2)剔除了所有的叶交换机,相当于砍掉了树的所有最下层分叉,而确定叶交换机的过程是用证明过的定理2和定理3,确保了确定叶交换机的正确性;步骤(3)更新了剩余树的新的节点结合,相当于把砍掉的最低层分叉变成了新的叶子节点.因此,我们提出的树型剪裁算法是正确的.

而每次进行树型剪裁的过程,就是确定每一层拓扑连接关系的过程,砍掉的叶交换机的下行端口的AFT中的地址就是和它直接相连的叶子的地址,如果某个下行端口AFT记录了多个地址,说明此端口通过哑设备连接了多个叶子节点.

为了更加形象的说明算法的执行过程和说明算法的正确性,我们通过一个具体的拓扑发现例子来说明树型剪裁算法是如何发现具体的网络拓扑结构的.如图2的网络拓扑结构,直接连接主机h8和h9的是一个集线器,图2右侧给出了网络中所有交换机的AFT,比如根节点S1的端口1的AFT在完整时应该是A11={S2,S4,S5,S6,h1,h2,h3,h4,h5},而图2中S1的端口1的AFT只含有主机1,我们进一步可以看到此网络节点的AFT完整性很差,基于完整AFT的方法[8～10]和基于下行端口完整的方法[11,12]根据这样的AFT是无法发现此网络的拓扑结构的,其它基于AFT的方法[14～22]算法复杂度高,而且无法完整发现此网络的拓扑结构.

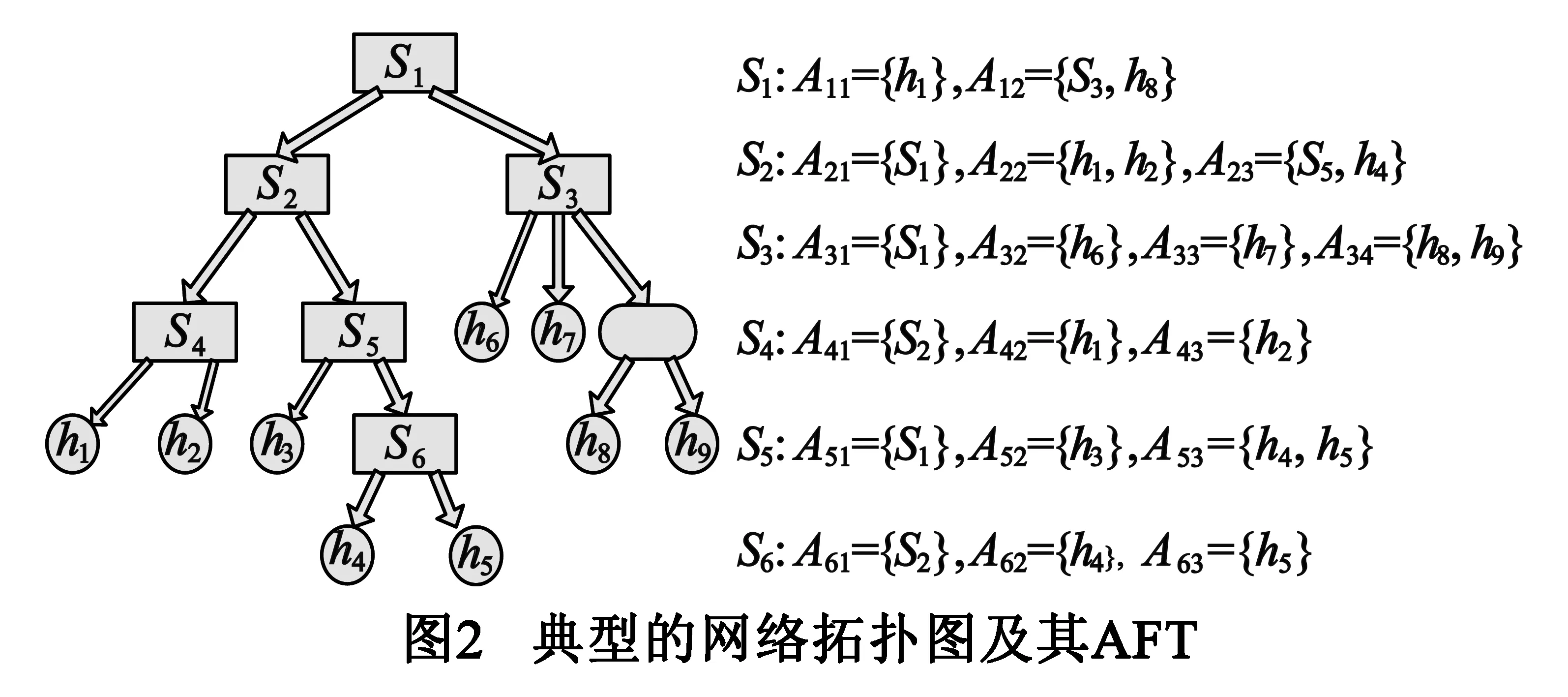
下面基于我们的树型剪裁算法来发现此网络的拓扑结构,在根交换机确定为S1后(通常将路由器下连子网中直接和路由器端口相连的交换机定为根交换机),将交换机的AFT和交换机入集合H,然后确定叶交换机,由于S1已经被确定为根交换机,我们首先从剩余的交换机中根据定理2选出备选的叶交换机集合,从图2中我们看到剩余交换机除了S2的两个端口(端口1和2)含有交换机的地址外,其它交换机都只有一个端口含有交换机的地址,因此,第一次算法求得的备用叶交换机为{S3,S4,S5,S6},再由定理3,对端口AFT含有多个叶子节点的项目作分析,只有S3的A16和S5的A53,但A16中的主机8和9并没有分布在其他交换机的不同端口上,而A53的主机4和5分布在两个端口A62和A63的AFT中,因此,S5被剔除掉,即算法求得的第一层叶交换机为{S3,S4,S6},而S5的端口3则被认为是通过哑设备(集线器)连接叶子节点8和9.剪裁掉第一层叶交换机及其相连的叶子节点,并将叶交换机变为新的叶子,AFT更新后如图3所示.

经过第一次剪裁后,剩余交换机为:{S1,S2,S5},其它叶交换机变化了新的叶子节点,图3中用圆形节点表示叶子节点,端口的AFT也进行了相应的更新,S1为根,剩余交换机S2和S5仅用定理2就可以确定S5为叶交换机,继续将S5及其下连的叶子节点h3和S6剪除,将S5更新为新的叶子节点,如图4(a)所示,继续进行剪裁直到剩余一个根节点S1为止,如图4(a)～(c)所示.其中图4中省略了相应的AFT的变化.

从剪裁的过程我们可以看到,在通过树型剪裁算法进行拓扑发现时,每次的剪裁过程记录了叶交换机和叶子节点的直接连接关系,将每次剪裁掉的节点一层层组合在一起就可以形成完整的拓扑结构.显然,下行约束是相对于要求下行端口AFT完整的更宽松的约束,它也可以应用在从连接根交换机的管理终端获取所有子网交换机AFT的场景[8～16],这也是获取AFT的必经场景,它不要求每个下行端口完整,只要求通过下行端口AFT能确定唯一的拓扑结构即可,根据下行约束的定义可以看到,下行约束是仅通过下行端口AFT得出唯一正确拓扑的最松约束,不符合下行约束的网络的下行端口AFT,仅仅通过下行端口的AFT是得不出唯一正确的拓扑结构的.即符合下行约束的AFT仅由下行AFT就可以确定唯一的拓扑结构,通过树型剪裁算法可以得出相应唯一正确的拓扑结构.

我们提出的树型剪裁算法是严格按照定理1～定理4执行的,而定理1～定理4是根据下行约束AFT的定义严格证明得出的符合下行约束AFT网络的特性,因此,符合下行约束AFT定义的网络一定可以通过树型剪裁算法推断出唯一正确的拓扑结构.而且算法也非常简单,算法复杂度低,为O(n2),其中n为网络中的节点数.另外,我们提出的树型剪裁算法只用到交换机的AFT,而不需要取得主机的AFT,现实网络中的大部分主机不一定配置SNMP协议,因此,树型剪裁算法对实际网络的拓扑发现非常适用.

4 实验仿真

我们的实验仿真使用BRITE[20]和NS2,其中BRITE用于生成符合幂率分布的网络节点拓扑连接关系,我们通过修改BRITE的拓扑生成代码,可以将BRITE生成的拓扑连接关系直接导入到NS2中生成相应的拓扑结构,如图5是一个BRITE生成的符合幂率分布的60个网络节点的连接关系,经过导入到NS2后生成的网络拓扑图.

由于我们在使用BRTIE生成拓扑邻接关系时,采用BA模型,即节点和拓扑连接是增量增长和优先连接,因此生成拓扑图以第一个节点即节点0为根节点,网络流量产生方式是由从根节点0每隔1秒逐个向其它节点发送FTP报文,如第一秒向第一个节点发送,第二秒向第二个节点,等等;另外,由于FTP报文在传输层使用的是TCP协议,会有相应的回执报文,因此,可以根据网络中的流量信息采用反向地址学习机制构造出各交换机的地址转发表,可以通过AFT的老化机制和人为去除的方式使得AFT不完整且下行端口AFT符合下行约束,手工去除AFT表项时,只要节点端口的AFT按满足定理1的条件去除,就可以保证节点的AFT满足下行最小约束.

由于树型剪裁算法只用到交换机的AFT,而不需要取得主机的AFT,因此,BRITE生成的拓扑图中的节点我们可以人工将其分为三种类型,第一种是交换机,第二种是终端,第三种是哑设备.具体划分方法是:将度数为1的节点即所有的叶子节点作为终端设备,如图5中的节点50;将小部分度数大于2的下层节点作为哑设备,如图5中的节点2和节点9;其余节点都作为交换机,如图5中的节点3和1.注意度数为2的节点不能划分为哑设备,因为这样的哑设备在基于AFT的拓扑发现方法中是不可能被发现的,如图5中的节点6和18.

仿真数据在一台Pentium IV 2.4GHz、内存为2G,操作系统为WIN7的计算机进行处理,对我们实验的所有由BRITE生成的拓扑结构,只要在构造AFT时,只要下行端口的AFT符合下行约束,算法就可以准确地发现正确的拓扑结构,进一步验证了文中的树型剪裁算法的拓扑发现结论,即:符合下行约束AFT定义的网络一定可以通过树型剪裁算法推断出唯一正确的拓扑结构.

虽然拓扑发现算法的正确性是衡量拓扑发现算法的最重要指标,时间性能对于拓扑发现算法也是很重要的,图6是生成的不同节点数的网络对应的树型剪裁算法的运行时间,图中以双纵坐标的方式显示,横坐标表示BRITE生成的拓扑结构中的节点数,包含交换机、终端及哑设备,纵坐标1表示算法对于不同节点数网络的拓扑发现时间,图例中用‘□’标记,纵坐标2表示相应的节点数网络中含有地交换机的个数,图例中用‘×’标记.从图6中我们发现,节点端口的AFT生成后,算法执行拓扑发现的时间是很快的,因此,实际网络中的拓扑发现的时延主要来源于采集所有交换机的AFT的时间.

另外,从图6中还可以看到,基本趋势是随着网络中节点数的增加,拓扑发现算法的运行时间是逐步递增的,如500个节点的网络拓扑发现时间和600个差不多,而800个节点的拓扑发现时间比700个节点的还要少,原因是500个节点的网络中含有的交换机数量和600个节点网络中的交换机数量差不多,而800个节点的网络中含有的交换机数量比700个节点网络中的交换机数量还要少,进一步说明了我们提出的树型剪裁算法仅依赖于交换机的AFT,而不需要主机的AFT,算法运行时间取决于网络中交换机的数量及其AFT的具体情况,仔细观察图6可以发现,网络中交换机的数量和算法运行时间的趋势是基本一致的.

由于目前拓扑发现仅基于下行端口的方法只有文[11,12]的工作,而且文[11,12]的方法要求下行端口的AFT完整,在下行端口AFT不完整时,无法发现正确的网络拓扑,因此,与我们提出的树型剪裁算法不具有可比性.

大部分的基于AFT的拓扑发现算法需要用到终端设备的AFT,这样需要网络中的主机都要配置SNMP,但现实网络中用户为了保护隐私,大部分主机默认是不配置SNMP的,这样还需要通过ARP取得主机的可达地址,而我们提出的树型剪裁算法只需要获取交换机的AFT,这对实际网络的拓扑发现非常有用,在实际网络中获取AFT时,可能会获取到部分支持SNMP的主机的AFT,因此,算法部署到实际网络环境时,需要根据sysServices MIB判断设备类型(这也是所有拓扑发现必须做的工作),并去除所有非交换机的AFT后,再运行树型剪裁算法.

5 部署应用

为了进一步验证算法在实际网络系统中的可行性和适用性,我们将算法部署应用到我们开发的网络资源主动管理系统中,

实际部署时我们发现,实际网络AFT缺失量并不是很大,可能和我们的实际网络环境规模相对较小有关,不需要进行整个子网的PING操作,子网的AFT完全满足最小下行约束,但AFT表中有部分不可达的设备,这可能由部分设备配置改变和部分设备迁移或宕机引起,因此,仍然需要对AFT中的IP地址进行PING操作,排除那些不可达的表项,但相对于PING整个网段,大大减少了PING操作,缩短了拓扑发现的实际时间,由于实际网络拓扑发现要下载AFT和进行PING操作,拓扑发现时间要比仿真实验的拓扑发现时间长很多,图7是主动网络管理系统进行实际拓扑发现的网络拓扑图.

6 未来工作

本文基于实际网络AFT不完整的情况,定义了三种约束,本文的作者基于最小下行约束,提出了一种树型剪裁算法,可以在AFT完整性较差的情况下发现网络的拓扑结构.本文的工作重点讨论了下行约束算法,显然研究有效的最小约束算法对物理拓扑发现是最有意义的,因为它可以充分利用所有AFT提供的有效信息,而不是只限于单个方向的有效信息,因此,后续工作,我们会对上行约束和最小约束算法逐步展开研究,同时本文也为其他学者提出了一个开放的课题,也期望其他学者提出他们的解决上行约束和最小约束AFT的算法.对于整个交换域的拓扑发现,我们可以在子网拓扑发现的基础上用文[15,16]的方法再进行子网间合并,当然,在后续工作中,如何将树型剪裁算法直接成功应用于整个交换域是我们的重要研究方向.

[1]Siamwalla R,Sharma R,Keshav S.Discovering internet topology[R].Cornell Univ,Ithaca,NY,1999.

[2]Bierman A,Jones K.Internet RFC-114,2000,Physical topology MIB[S].

[3]Dawes N,Schenkel D,Slavitch M.Method of determining the topology of a network of objects[P].USA:6231997,2002-06-07.

[4]Schenkel D,Slavitch M,Dawes N.Method of determining topology of a network of objects which compares the similarity of the traffic sequences/volumes of a pair of devices[P].USA:598462,1999-07-02.

[5]邱林,张建忠,吴功宜.基于端口流量的物理网络拓扑发现方法研究[J].计算机工程与应用,2002,22(4):171-172.

Lin Q,Jianzhong Z,Gongyi W.Physical topology discovery method study based on ports traffic[J].Computer Engineering and Application,2002,22(4):171-172.(in Chinese)

[6]Son MH,et al.Physical topology discovery for metro ethernet networks[J].ETRI Journal,2005,9(4):175-186.

[7]Black R,Donnelly A,Fournet C.Ethernet topology discovery without network assistance[A].Proc of the 12th IEEE Int’l Conf.on Network Protocols[C].Los Alamitos:IEEE,2004.130-159.

[8]Breitbart Y,Garofalakis M,Martin C,Rastogi R,Seshadri S,Silberschatz A.Topology discovery in heterogeneous IP networks[A].Proc of the INFOCOM[C].New York:IEEE,2000.85-94.

[9]Breitbart Y,Garofalakis M,Jai B,Martin C,Rastogi R,Silberschatz A.Topology discovery in heterogeneous IP networks:The NetInventory system[J].IEEE/ACM Trans on Networking,2014,12(3):221-234.

[10]Bejerano Y,Breitbart Y,Garofalakis M,Rastogi R.Physical topology discovery for large multi-subnet networks[A].Proc of the IEEE INFOCOM[C].New York:IEEE Press,2003.162-172.

[11]郑海,张国清.物理网络拓扑发现算法的研究[J].计算机研究与发展,2002,39(3):264-268.

Zheng H,Zhang GQ.An algorithm for physical network topology discovery[J].Journal of Computer Research and Development,2002,39(3):264-268.(in Chinese)

[12]陈福,杨家海,杨扬 网络拓扑发现新算法及其实现[J].电子学报,2008,36(8):1620-1625.

Fu C,Jiahai Y,Yang Y.New algorithms on IP network topology discovery and Its implement[J].Acta Electronica Sinica,2008,36(8):1620-1625.(in Chinese)

[13]Lowekamp B,O’Hallaron DR,Gross TR.Topology discovery for largeethernet networks[A].Proc of the ACM SIGCOMM[C].New York:ACM,2001.57-68.

[14]孙延涛,吴志美,石志强.基于地址转发表的交换式以太网拓扑发现方法[J].软件学报,2006,17(12):2565-2576.

Yantao S,Zimei W,Ziqiang S.Amethod of topology discovery for switched ethernet based on address forwarding tables[J].Journal of Software,2006,17(12):2565-2576.(in Chinese)

[15]Bejerano Y.Taking the skeletons out of the closets:A simple and efficient topology discovery scheme for large multisubnet networks[A].Proc Of IEEE INFOCOM[C].IEEE Press,2006.1-13.

[16]Bejerano Y.Taking the skeletons out of the closets:A simple and efficient topology discovery scheme for large ethernet lans[J].IEEE/ACM Trans on Networking,2009,17(2):1205-1218.

[17]Breitbart Y,Gobjuka H.Characterization of layer-2 unique topologies[J].Information Processing Letters,2008,105(2):52-57.

[18]Gobjuka H,Breitbart Y.Characterization of layer-2 unique topologies in multisubnet local networks[A].Proc of IEEE LCN[C].IEEE Press,2006.522-524.

[19]Gobjuka H,Breitbart Y.Ethernet topology discovery for networks with incomplete information[A].Proc of IEEE ICCCN[C].IEEE Press,2007.613-620.

[20]Gobjuka H,Breitbart Y.Finding ethernet-type network topology is not easy[R].TR-KSU-CS-207-03,Kent State University,2007.

[21]Gobjuka H,Breitbart Y.Discovering network topology of large multisubnet ethernet networks[A].Proc IEEE LCN[C].IEEE Press,2007.230-237.

[22]Gobjuka H,Breitbart Y.Ethernet topology discovery for networks with incomplete information[J].IEEE/ACM Trans on Networking,2010,18(4):1220-1233.

张 宾 男,1976年生于河南新乡.总参第六十三所博士后.研究方向为网络管理与测量、网络异常检测.

E-mail:zhang-bin163@163.com

刁兴春 男,1964年生于江苏泰兴.硕士研究生,研究方向为网络管理与数据质量.

A Physical Topology Discovery Method Based on AFT of Downstream Constraint

ZHANG Bin,DIAO Xing-chun,LIU Yi,YU Yun,YUAN Zhen,DING Chen-lu,JIANG Guo-quan

(The63rdResearchInstitute,Nanjing,Jiangshu210007,China)

Network physical topology discovery is very important for network management and application,the physical topology discovery based on AFT is a hot topic on current study.However,the incomplete AFT of network nodes in real network leads to the hardness of physical topology discovery.Based on decreasing the demand for the completeness of AFT in topology discovery,this paper defines three constraints of AFT,and proposes a tree-chopping algorithm based on AFT satisfying downstream constraint to discover the physical topology of a subnet.The proposed algorithm decreases the constraints for the completeness of AFT greatly,and demands the loosest constraint in physical topology discovery relying solely on downstream ports.The correctness and efficiency of the proposed algorithm is verified by the simulation experiment,and the algorithm applicability to real network is verified by deploying the algorithm in a real network management system.

physical topology discovery;address forwarding table;network management;

2014-10-10;

2015-03-11;责任编辑:蓝红杰

江苏省博士后科研资助项目(No.1402138C);国家自然科学基金(No.61371196,No.1462009);中国博士后科学基金(No.2015M582832)

TP393

A

0372-2112 (2016)08-1864-09