一种基于神经网络的广义熵模糊聚类算法

李 凯,曹 喆

(河北大学计算机科学与技术学院,河北保定,071000)



一种基于神经网络的广义熵模糊聚类算法

李 凯,曹 喆

(河北大学计算机科学与技术学院,河北保定,071000)

以模糊聚类为基础,将广义熵引入到模糊聚类的目标函数中,提出一种基于模糊熵的模糊聚类的统一形式,即广义熵模糊聚类模型;利用增广拉格朗日求解方法,以及Hopfield神经网络和复突触神经网络解决了基于广义熵的目标函数的优化问题,提出了基于神经网络的广义熵模糊聚类算法,表明了使用神经网络求解的收敛性;同时,给出一种用于确定增广拉格朗日乘子的迭代方法.实验中选取人工生成数据集和UCI标准数据集对提出的算法进行了实验研究,并与常用的聚类算法进行了性能比较.

模糊聚类;广义熵;增广拉格朗日方法;神经网络

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.016

1 引言

为了克服FCM对噪声的影响,一些学者将模糊熵引入到目标函数J1(U,V) 中,提出了基于熵的聚类算法[7～11];另外,一些学者基于目标函数J2(U,V),通过加入调整项,提出了竞争凝聚算法CA,以此解决聚类数的自动确定问题[12],之后,学者们在CA聚类算法的基础上,将约束条件或样本间的度量引入到J2(U,V)中,提出了半监督聚类算法[13-14];最近,Maraziotis[15]通过对约束进行量化,并将其引入到J2(U,V),提出了一种半监督模糊聚类算法.可以看到,以上介绍的聚类算法,学者们主要采用Jm(U,V)的特殊形式J1(U,V)或J2(U,V),通过引入调整项,并借助拉格朗日方法,获得相应的模糊聚类算法.为了研究一般情形下的聚类算法,Pedrycz等[16]将监督信息引入到Jm(U,V)中,给出了一般形式的目标函数,然而,他们并未对此种优化问题给出求解方法,只是使用了特殊的目标函数J2(U,V);另外,Wei等[17]试图使用神经网络解决一般目标函数的模糊聚类,遗憾的是该方法却存在一些问题[18].针对此种情况,本文研究了一般情形下的目标函数构成的优化问题的模糊聚类.

2 广义熵模糊聚类的目标函数

(1)

其中α>0且α≠1,δ为参数.因此,广义熵模糊聚类的优化问题为

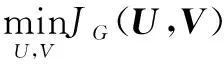
(2)

由式(1)知,当m=1且α→1时,式(1)成为Karayiannis[9]等提出的聚类算法.当α→1时,式(1)为Wei等[17]提出的聚类算法,因此,优化问题式(2)可以视为它们的统一形式.

另外,由式(2)中的目标函数可以知道,当m=α时,该优化问题可以通过拉格朗日方法求解,对于此种情况,我们已经进行了研究[19];然而,当m≠α时,使用传统拉格朗日求极值方法对式(2)求解是不可行的.实际上,对于优化问题式(2),可以使用启发式方法求解,例如,禁忌搜索、变邻域搜索等.本文主要使用神经网络方法对其进行求解.

3 广义熵模糊聚类的神经网络方法

为了求解优化问题式(2),本文使用增广拉格朗日方法,Hopfield神经网络与复突触神经网络求解.

3.1 使用Hopfield网络求解聚类中心

对于优化问题式(2),其增广拉格朗日函数为

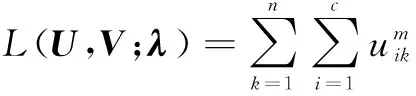
(3)

其中λk(k=1,2,…,n)为拉格朗日乘子,λ=(λ1,λ2,…,λn),γ是一个充分大的数.由式(3)知道,它是一个关于聚类中心vi=(vi,1,vi,2,…,vi,N)(i=1,2,…,c)的二次函数,通过将二维下标转化为一维下标,且使用具有q=c×N个神经元的Hopfield神经网络求解,下面给出了求解聚类中心的Hopfield神经网络的权值,外部输入和激励函数.

NET=W·V+I

其中NET=(net1,net2,…,netq)T,

W=(wij)q×q,V=(v1,v2,…,vq)T,I=(i1,i2,…,iq)T,

(4)

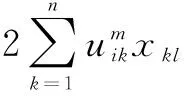
i=1,2,…,c;l=1,2,…,N

(5)

j=1,2,…,q;i=1,2,…,q,

(6)

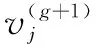
(7)

其中上角标的g为迭代次数,δj是一个较小的可调正数,详细推导可参见文献[17].

3.2 使用复突触神经网络求解模糊隶属度

令dik=‖xk-vi‖2,则式(3)变为

(8)

+(u(k-1)×c+c)md(k-1)×c+c

+γ(u(k-1)×c+1+u(k-1)×c+2+…+u(k-1)×c+c)2

+δ(21-α-1)-1((u(k-1)×c+1)α+(u(k-1)×c+2)α+…

+(u(k-1)×c+c)α)

+(λk-2γ)(u(k-1)×c+1+u(k-1)×c+2+…+u(k-1)×c+c)

+γ-λk-δ(21-α-1)-1]

(9)

由m和α的取值可知,函数式(9)可能为一个高次的函数,鉴于此种情况,本文使用复突触神经网络对其进行优化.根据聚类中心vi(i=1,2,…,c)在第二层循环中其值不变以及最后一行为常数,因此,在下面的优化中对这些项进行删除.

j=1,2,…,s

(10)

网络输入的矩阵形式可表示为:

NET=W·U+Z·U+Y·U+I

(11)

其中Z=(zij)s×s,Y=(yij)s×s,U=(u1,u2,…,us)T,I=(i1,i2,…,is)T,s=n×c.

定义矩阵U和Y<α-1>如下:

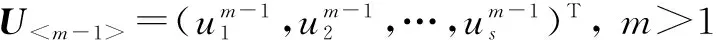
为了获得求解隶属度的神经网络,利用式(11)得到如下的能量函数:

(12)

比较式(9)和式(12),获得了如下的对应关系:

(13)

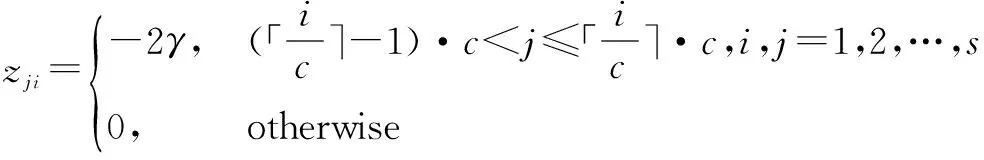
(14)

i,j=1,2,…,s

(15)

ij=2γ-λkj=1,2,…,s;k=「j/c⎤

(16)

其中「x⎤为不小于x的最小整数.利用对称矩阵和向量具有LTAR=RTAL关系(其中A为一个对称矩阵,L和R分别为列向量),则式(12)变为

(17)

对于此式,可以理解为将-(1/m)UT、-(1/2)UT、-(1/α)UT和-UT分别乘以式(18)中右边第一项、第二项、第三项和第四项,这就意味着将U反馈给权值W,将新的U反馈给权值Z,将U<α-1>反馈给权值Y,从而得到一种具体的复突触神经网络,其中网络输入的权值矩阵为:

NET=W·U+Z·U+Y·U<α-1>+I

(18)

激励函数f按照如下方法确定,其中ωj是一个较小的可调整正数,

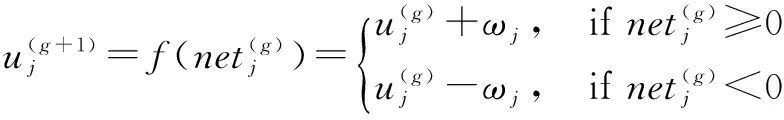
j=1,2,…,s.

(19)

3.3 增广拉格朗日乘子的确定

为了确定式(16)中的拉格朗日乘子,考虑如下的优化问题:

(20)

其增广拉格朗日函数为:

L(U,V;λ)

(21)

关于式(20)和(21)有如下结论[20]:如果U*,V*是问题式(20)的最优解,λ*为由拉格朗日乘子构成的向量,则当γ充分大时,U*,V*是式(21)的极小值点,且式(20)和(21)等价.为此,针对式(21),先给定λ*的一个初始值λ(p),并用该值求解优化问题式(21),设其解为U(p+1),这样可以得到如下等式:

▽UL(U(p+1),V;λ(p))

+2γφk(U(p+1)))▽φk(U(p+1))

=0

可以看到,如果U*是式(20)的最优解,则有

从而有

(22)

3.4 广义熵模糊聚类算法GEFCM

通过上面的推导,下面给出具体的算法,并将该算法记为GEFCM(Generalized Entropy FCM):

4 实验结果与分析

为了表明提出的算法GEFCM的有效性,实验中选取了7个数据集进行了研究,其中Arti3是人工生成的三维线性可分数据集,具有3个类别和150个数据样本,且每类中的数据点个数均为50.另外6个数据集来自于UCI,分别为Iris,Breast-w,Wine,Heart,Ionosphere和Australian.实验中选择的参数值分别为γ=1000,δv=0.5,δu=0.2,ε=0.001,Δv=0.0001和Δu=0.0001.为了评价聚类的性能,实验中选择了聚类正确率作为评价指标,即正确聚类的个数除以样本总数.实验结果如表1至表7所示.

表1 Arti3数据集的实验结果

表2 Iris数据集的实验结果

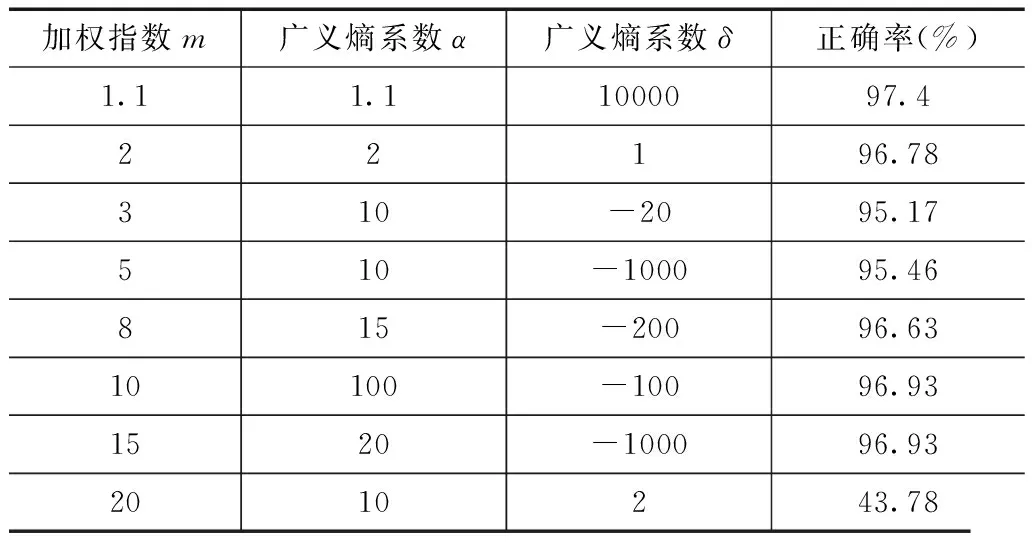
表3 Breast-w数据集实验结果

表4 Wine数据集实验结果

表5 Heart数据集实验结果

表6 Ionosphere数据集实验结果

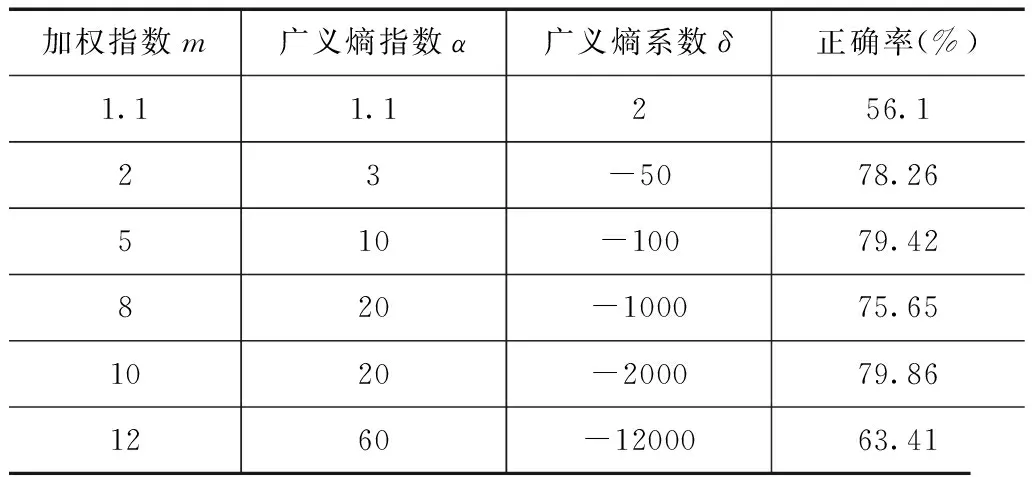
表7 Australian数据集实验结果

由实验结果可以看到,对于可分性数据集Arti3,当加权指数和广义熵指数相等且接近于1时,获得了较好的聚类结果;然而,对于选择的UCI标准数据集,当加权指数和广义熵指数相等且接近于1或加权指数等于2时,其聚类结果并不一定是最好的,例如,对于Wine数据集,当m=2且α=2时,获得了最好的聚类正确率85.96,然而,当α=2时,此时的广义熵并不是模糊熵,表明了基于模糊熵的聚类未必获得更好的聚类结果,从而充分说明引入广义熵模糊聚类的重要性.

另外,为了验证提出的算法GEFCM的性能,实验中也选取了FCM、PPSO-FCM[21]以及SSWFCM算法[22]在标准数据集进行了比较,实验结果如图2所示.

可以看到,基于广义熵的模糊聚类算法在选取的数据集上的聚类正确率都高于FCM、PPSO-FCM和SSWFCM,且此时加权指数m的取值并不仅限制在1或2两个值,从而表明提出的广义熵目标函数聚类的合理性.

5 结论

本文通过引入广义熵,提出了广义熵模糊聚类模型,统一了基于熵的模糊聚类算法,使用Hopfield神经网络和复突触神经网络并结合增广拉格朗日乘子法解决了基于广义熵的模糊聚类问题,提出了基于神经网络的广义熵模糊聚类算法,给出了拉格朗日乘子的确定方法.在实验中,选取人工数据集和UCI数据集对提出的算法性能进行了测试,并与其它算法进行了性能比较,表明了提出的算法对数据聚类的有效性.

[1]Timothy C H,James C B,Christopher L,et al.Fuzzy c-Means algorithms for very large data[J].IEEE Transactions on Fuzzy Systems,2012,20(6):1130-1146.

[2]慕彩红,霍利利,刘逸,刘若辰,焦李成.基于小波融合和PCA-核模糊聚类的遥感图像变化检测[J].电子学报,2015,43(7):1375-1381.

Mu Caihong,Huo Lili,Liu Yi,Jiao Licheng.Change detection for remote sensing images based on wavelet fusion and PCA-kernel fuzzy clustering[J].Acta Electronica Sinica,2015,43(7):1375-1381.(in Chinese)

[3]Yang M S,Tsai H S.A gaussian kernel-based fuzzy c-means algorithm with a spatial bias correction[J].Pattern Recognition Letters,2008,29(12):1713-1725.

[4]刘兵,夏士雄,周勇,韩旭东.基于样本加权的可能性模糊聚类算法[J].电子学报,2012,40(2):371-375.

Liu Bing,Xia Shixiong,Zhou Yong,Han Xudong.A sample-weighted possibilistic fuzzy clustering algorithm[J].Acta Electronica Sinica,2012,40(2):371-375.(in Chinese)

[5]Jacek M L.Fuzzy c-ordered-means clustering[J].Fuzzy Sets and Systems,2016,286,114-133.

[6]Ding Y,Fu X.Kernel-based fuzzy c-means clustering algorithm based on genetic algorithm[J].Neurocomputing,doi:10.1016/j.neucom.2015.01.106.

[7]Krishnapuram R,Keller,J M.A possibilistic approach to clustering[J].IEEE Transactions on Fuzzy Systems,1993,1(2):98-110.

[8]Krishnapuram R,Keller J M.The possiblistic means algorithms:insights and recommendation[J].IEEE Transactions on Fuzzy Systems,1996,4(3):385-393.

[9]Karayiannis N B.MECA:maximum entropy clustering algorithm[A].IEEE world congress on computational intelligence,Proceedings of the third IEEE conference on fuzzy systems[C].Orlando:IEEE,1994.630-635.

[10]Ichihashi H,Miyagishi K,Honda K.Fuzzy c-means clustering with regularization by K-L information[A].Proceedings of the 10th IEEE international conference on fuzzy systems[C].Melbourne:IEEE,2001.924-927.

[11]Yasuda M,Furuhashi T,Matsuzaki M,et al.A study on statistical mechanical characteristics of fuzzy clustering[A].Proceedings of IEEE International Conference on Systems,Man,and Cybernetics[C].Tucson:IEEE,2001.2415-2420.

[12]Frigui H,Krishnapuram R.Clustering by competitive agglomeration[J].Pattern Recognition,1997,30 (7):1109-1119.

[13]Grira N,Crucianu M,Boujemaa N.Active semi-supervised fuzzy clustering[J].Pattern Recognition,2008,41 (5):1834-1844.

[14]Gao C F,Wu X J.A new semi-supervised clustering algorithm with pairwise constraints by competitive agglomeration[J].Applied Soft Computing,2011,11(8):5281-5291.

[15]Maraziotis I A.A semi-supervised fuzzy clustering algorithm applied to gene expression data[J].Pattern Recognition,2012,45:637-648.

[16]Pedrycz W,Amato A,Lecce V D,et al.Fuzzy clustering with partial supervision in organization and classification of digital images[J].IEEE Transactions on Fuzzy Systems,2008,16(4):1008-1026.

[17]Wei C,Fahn C.The multisynapse neural network and its application to fuzzy clustering[J].IEEE Transactions on Neural Networks,2002,13(3):600-618.

[18]Yu J,Hao P W.Comments on “The multisynapse neural network and its application to fuzzy clustering”[J].IEEE Transaction on Neural Networks,2005,16(3):777-778.

[19]Li K,Ma H Y,Wang Y.Unified model of fuzzy clustering algorithm based on entropy and its application to image segmentation[J].Journal of Computational Information Systems,2011,7(15):5476-5483.

[20]刘健,王晓明著.鞍点规划与形位误差评定[M].大连:大连理工大学出版社,1996.

Liu Jian,Wang Xiaoming.Saddle Point Programming and Geometric Error Evaluation[M].Dalian:Dalian University of Technology Press,1996.

[21]Liu H,Yih J M,Wu D B,Liu S W.Fuzzy c-mean clustering algorithms based on picard iteration and particle swarm optimization[A].Proceedings of International Workshop on Education Technology and Training[C].Washington:IEEE,2008.838-842.

[22]Zhang X B,Huang H,Zhang S.A FCM clustering algorithm based on semi-supervised and point density weighted[A].Proceedings of IEEE International Conference on Intelligent Computing and Intelligent Systems[C].Xiamen:IEEE,2010.710-713.

李 凯 男,1963年出生,河北保定人.2005年毕业于北京交通大学计算机与信息技术学院,并获得工学博士学位.主要从事机器学习、模式识别、数据挖掘等方面的研究.

E-mail:likai@hbu.edu.cn

曹 喆 女,1991年出生,河北邢台人,硕士研究生.主要从事机器学习和数据挖掘等方面的研究.

A Fuzzy Clustering Algorithm with Generalized Entropy Based on Neural Network

LI Kai,CAO Zhe

(SchoolofComputerScienceandTechnology,HebeiUniversity,Baoding,Hebei071000,China)

Based on fuzzy clustering,an unified form is presented for fuzzy clustering algorithm based on fuzzy entropy by introducing the generalized fuzzy entropy into objective function of fuzzy clustering,namely generalized entropy’s fuzzy clustering model.Optimization problem for generalized entropy’s objective function is solved using Hopfield neural network and multiple synapses based on augmented Lagrange method.After that,the generalized entropy’s fuzzy clustering algorithm based on neural network is presented.And convergence of neural network is shown.At the same time,iterative method is given to determine Lagrange multipliers.In experiments,a synthetic data set and some standard UCI data sets are chosen to conduct some experimental studies.And clustering performance is compared with commonly used clustering algorithms.

fuzzy clustering;generalized entropy;augmented Lagrange method;neural network

2015-12-08;

2016-03-18;责任编辑：蓝红杰

国家自然科学基金(No.61375075)

TP18

A

0372-2112 (2016)08-1881-06