从学生概念学习视角探究数学概念教学

常 宁，王守哲，韩花荣

(喀什大学 教育科学学院， 新疆 喀什 844000)



从学生概念学习视角探究数学概念教学

常 宁，王守哲，韩花荣

(喀什大学 教育科学学院， 新疆 喀什 844000)

数学概念在数学学习过程和教学中起着十分重要的作用。本文通过对数学概念和学生获得数学概念过程的分析，从概念形成和概念同化角度入手，在学生的认知结构、知识经验和抽象概括方面提供教学方法让学生抓住数学概念的本质属性，并结合中学某一具体案例作出说明解释。

数学概念；概念学习；概念教学

数学概念是学生学习数学的一个重要组成部分，它既是数学学习的逻辑起点，也是数学思维的核心。在数学学习过程中，如果对基本概念理解不透彻，会导致计算错误，思维混乱，推理出现偏差。概念的错误理解会是造成诸多学生成绩不理想的因素之一。

1 数学概念及对数学概念学习的分析

1.1 数学概念

数学概念是人类对数量关系和现实世界空间形式的概括反映，是建立数学法则、公式、定理的基础,也是运算、推理、判断和证明的基石，更是数学思维、交流的工具。[1]一般来说，数学概念源于俩方面：一方面源于人类对生活客观经验的总结及数量关系和空间逻辑关系的推导。另一方面是在已有的数学理论基础上进一步建构。数学概念是对数学本质属性的反应，遵循严密的逻辑结构和数学法则。如几何证明、三角函数、向量运算法则等，这类概念对数学的理论建构发挥着重要作用。

1.2 数学概念学习过程的分析

1.2.1 数学概念形成和概念学习过程

赫尔在对人工概念进行研究时提出了概念形成，并提出了联想理论，在此基础上布鲁纳对人工概念进一步研究提出假设考验说。奥苏伯尔对概念形成也进行了心理描述。众多心理学家对概念形成达成共识的同时，提出人们对同类事物中若干不同例子进行感知、分析、比较和抽象，以归纳方式概括出这类事物本质属性而获得概念的方式[2]。

数学概念学习在建立在概念形成的基础上，通过具体例子→观察共性→抽象本质→形成定义→强化概念→形成概念→概念应用，遵循一系列逻辑关系。如同学们在学习等差数列时，首先我们举出两组数字：100，98，96，94，92；5，10，15，20，25，观察两组数字的共性，发现每一项与前一项的差是同一个常数的本质，继而形成等差数列的定义，形成定义的同时进一步强化说明公差不仅仅是整数，也可以是小数、分数，进而形成等差数列概念，达到对等差数列概念的熟练应用。数学概念的建立，无论从何种层面来说，都要抓住该数学概念的核心特点。

1.2.2 数学概念同化和概念学习过程

学生学习数学知识并不是空着脑袋进入课堂的，而是建立在原有知识经验基础上进行学习，在定义形式陈述新概念时，学生主动地与其认知结构中的有关概念进行相互作用，也就是说学生原有的经验与新的经验结合，理解新概念的本质属性，从而形成新概念，这种获得概念的方式叫做概念同化。

概念同化的阶段可表示为：给出定义→与原认知结构建立联系→区别于原认知结构的概念→将新概念纳入原有概念体系之中→获得新概念。如我们在学习等比数列时，我们在理解等差数列的基础上，了解等比数列每一项与前一项的公比q是一个常数，但此时的常数公比q又有区别与等差数列的公差d(q≠0，公差d可以等于0)，这两个概念既有联系又有区别。最后通过练习、复习及习题的讲解使等比数列概念在认知结构中得到巩固。

2 数学概念学习的影响因素

影响数学概念学习的影响因素有很多，从学生角度来讲，不同学生对数学概念的接受和理解程度往往各不相同。简单分析以下几个主要因素，为教学提供参考。

2.1 原有认知结构

学生在学习数学概念时，往往是从他原有的认知结构或知识经验出发，认识、理解和区分概念之间的各种联系和区别。就概念形成来说，学生必须具有“刺激模式”相关方面的相关图式，也就是说，应具有与该数学概念方面相关的知识。就概念同化来说，要想掌握新的概念就必须掌握那些作为定义的概念，在原有概念的基础上进行进一步建构。因此，学生在学习数学概念时，我们应该注重学生原有的认知结构中的有关知识和经验，从中抽取概念的本质属性，淡化非本质属性。

2.2 感性材料

概念的形成需要有丰富的经验和相关背景，对感性材料进行抽象。而概念同化主要是对以往知识经验的概括。因此，感性材料对概念的形成至关重要。感性材料太少或知识经验欠缺，学生对概念的理解就会不充分、不丰富，难以辨别各种对象的本质属性，更不易理解概念的内涵和外延。数学概念是学生不断感知经验的活动过程，是主体不断对感性材料加工、修正，最终达到主体对感性材料建构的过程，随着个人对感性材料理解的加深，知识经验也随之加深，主体对感性材料的建构就不断发展、完善。

2.3 抽象概括能力

所谓抽象能力，是指把概念中各个个别对象的共同属性抽取出来，舍弃各个个别对象的其他属性。而概括能力是由给定的对象集合进到讨论容量更大的且包含前者的集合的中间过程。心理学研究表明：抽象和概括是人们形成和掌握概念的直接前提。因此，学生要掌握数学概念就必须有一定得抽象概括能力，“抽象”是概念形成必不可少的步骤，“概括”是概念同化的必要环节。抽象概括能力差，就会抓不住事物的本质属性，尤其是数学概念的本质属性，不能明确数学概念的内涵和外延。

3 数学概念教学过程

数学概念学习过程应是有意义的接受学习和发现学习，其实质就是把数学知识(指教材)经过学生的思维活动积极主动地与学生的原有认知结构进行建构。因此，教师在教学过程中要注重学生的原有认知结构，结合学生的知识经验，加强学生的抽象概括能力，以达到更好的让学生掌握数学概念的目的。

3.1 合理引入情景和问题，建立优良的数学认知结构

在数学教学中，为了使学生更容易接受和掌握概念，教师应该先创设有关数学概念的相关情景，想方设法唤起学生原有认知结构中的有关知识和经验。如，学生们在学习“平行六面体”概念时，教师可让学生们先回忆有关“平行四边形”概念和性质，再回忆棱柱的面是什么样子，三棱柱以及四棱柱的形状，然后让同学们发现问题，“平行六面体”与以往的棱柱有什么不同，这样就为学生理解平行六面体概念奠定了基础。新概念和学生原有认知结构中的知识产生联系，从而形成新的概念。

学生在学习新课时，开始可能会接触到一系列新的概念、公理、定理以及思想方法，这些简单的定理、公式不可能被原有认知结构所同化，这时只能从现实生活的实例、模型中抽象概括。针对这种状况，教师在教学时要尽可能的采用实物、模型加以弥补，突出和辨析各种对象的本质属性。例如，教师在讲解几何中垂直概念时，可以举出生活中人们在建造房屋时用到“铅垂线”测量房屋的笔直程度，再引出几何数学中所指的垂直是我们所说的90°角，最后在练习和解题中对垂直的概念加以利用和证明。在平面几何学习入门阶段，处于建立新的数学认知结构过程，而教师的引导对于学生形成新的数学认知结构显得十分重要，这个新建的数学认知结构关系到今后数学学习的好坏，也是今后数学学习的基础。

3.2 重视学生过去的知识经验，基于学生旧知识上建立新概念

学生在学习每一个公式、定理时，教师都应该让学生在自己已有的知识体系上，清楚的知道怎样一步步的得出什么结论，运用了以往的哪些概念、定理或公式，运用了什么方法。要知其所以然，不能只记住条件或结论。如学生在高中学习三角函数概念时，教师在让学生知道正弦公式、余弦公式的基础上推导二倍角公式，让学生在已有知识的基础上由sin(α+β)=sinαcosβ+cosαsinβ得出sin(α+α)=sinαcosα+cosαsinα=2sinαcosα，而不是让学生直接背下sin2α=2sinαcosα。同理，余弦函数的二倍角公式和正切函数的二倍角公式都是在学生学完余弦公式和正切公式的基础上建立的，也就是说，有些新数学概念是在学生旧知识基础上建立的。数学概念学习是一个积极思维活动的过程，教师切不可脱离学生已有的知识经验而把数学概念看成孤立的、静止的，要在学生已有知识经验的基础上培养学生有意义学习的倾向。新旧概念存在某些相似性的同位关系，例如，对数函数的相关性质是在指数函数相关知识基础上建立的，立体几何中的相关概念的学习是在平面几何概念的基础上获得的。

鉴于数学概念产生的背景不同，教师应充分考虑学生的原有知识经验，必要时可以导入新概念的相关情景，让学生头脑中原有概念与新概念产生对比、分类，区分新旧概念之间的异同，认识新旧概念之间的关系，这样才有利于学生头脑中知识结构形成有机网络。

3.3 让学生抓住数学概念的本质属性，加强学生的抽象概括能力

教师在引导学生学生学习数学概念时，要让学生练习对概念本质属性与非本质属性的区分，要采用适当的方法让本质属性明显一些，以便于学生对概念的抽象概括，在讲到数学概念本质属性时可加强语气，用彩色粉笔做重点突出。有时也可直接指出哪些是概念的非本质属性，如在刚学习函数这一概念时，学生往往误认为只有y随x的变化而变化的才叫做y是x的函数，而函数概念的本质属性实则是对于变量x在定义域内的每一个值，变量y都有唯一确定的值与它相对应，举出肯定实例y=x0，对于x取的每一个值(非0)，y都有惟一确定的值1与它相对应，教师在讲解函数概念时可在“唯一”下面点上两个小点进一步突出概念本质属性，又如，学生在学习三角形高线时，往往认为只有在三角形三边内的垂线才称为高线，把非本质属性(垂线在边内、垂线在边上、垂线与边重合)误认为本质属性，因此，及时指出概念反映的非本质属性有利于突出概念的本质属性，从而让学生正确掌握概念。

在几何教学中，学生在感知几何图形时，在抽象概括它的本质特征过程中，往往会受到非本质属性的影响，尤其是非本质属性表现的十分明显或强烈时。如在学习等腰三角形时，顶点画在左边，底边画在右边，有些学生可能就不认为这是等腰三角形了，所以教师要引导学生抽象概括等腰三角形的本质，让学生概括出有俩条边相等的三角形就是等腰三角形。

4 结合概念教学理念的案例展示(向量加法运算及其几何意义一课的引入)

4.1 创设情境，引入问题

情景-唐僧师徒四人西天取经的路上，遇到一块大石头阻住去路，师兄弟三人就“人多力量大”这句话发生争论，提出几个问题让学生根据已有生活经验做答。

教师：提出问题1. 悟空师兄弟每人都以1000N的力推石头，则石头受到的合力是3000N吗？

问题2. 唐僧当年取经路线是先到新疆，再往天竺，若悟空单独前往，可以直接飞往西天，两种走法的路程相同吗？位移呢？

(设计意图：教师以生动有趣的小故事为载体创设问题情景，贴近学生生活，激发学生好奇心和求知欲，教师提出的两个问题有意识地将物理中力、位移的合成与即将学习的知识形成类比，形成优良的数学认知结构。)

学生：石头收到的合力不一定是3000N。

两种走法路程不同，位移相同。

(让学生充分利用已有的认知结构去探索和解决问题，在以前学过的物理知识基础上向本节要学的数学概念上靠近，新知识建立在原有认知结构上。)

4.2 信息交流，揭示规律

教师：某同学从家中A处出发，向正南方向行走500m到达超市，买了文具后沿着北偏东60°方向行走200m到达学校C处，如图1。此同学两次位移的总效果是什么？

学生：两次位移的总效果是从A到达了C处。

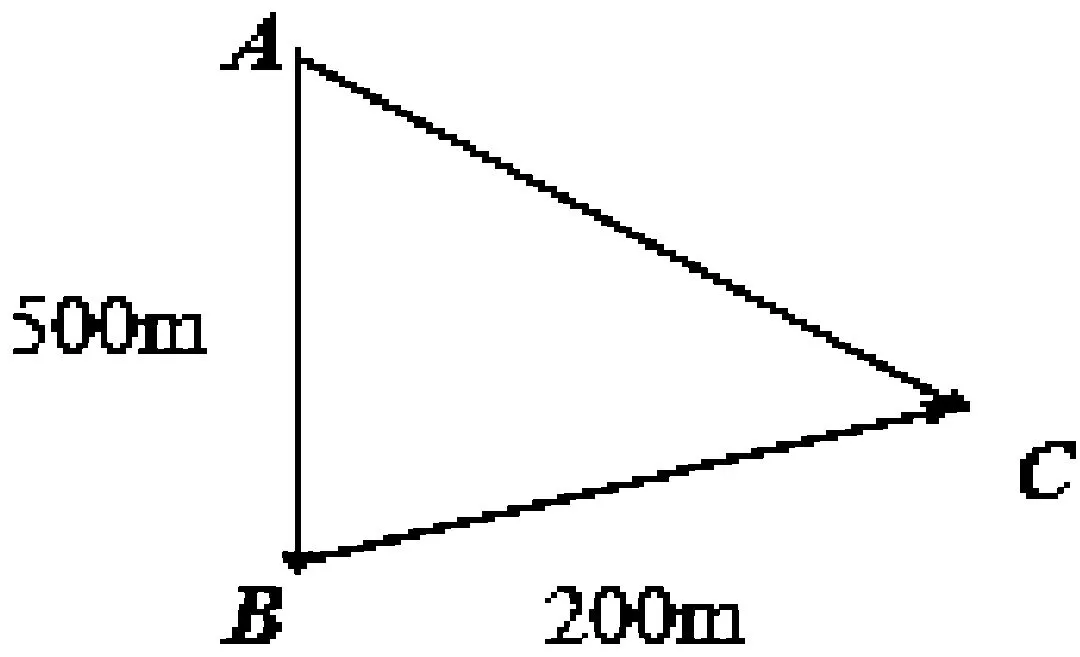
图1

教师：那我们在上这节课之前学过向量的表示方法，能用向量表示位移吗？

学生：思考.....

教师：那看到这个图我们能联想到以前学过的知识吗？

学生：有点像我们在物理学中学过力的正交分解。

教师：力的正交分解遵循什么法则呢？

学生：在平面直角坐标系里分解力、力的合成，三角形法则、平行四边形法则，遵循矢量加法法则。

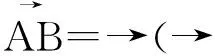
图2

(设计意图：关注学生过去的知识经验，学生在充分理解向量概念的前提下提出向量加法法则，在力学知识的基础上建立新概念，从而让学生自己揭示规律)

4.3 深化提高，抽象概括

教师：那么学生从以下练习题中看能否得出

教师：同学们在向量加法法则里发现什么了呢？能不能用自己的话说一下。

学生：老师我好像发现向量求和得出的和向量起点是向量→(→量)的起点，终点是向量→(→点)的终点。

教师：对的，那么向量加法和数量加法是否一样呢？

学生：物理学里的力合成是矢量加法，所以的向量的也应该是矢量加法，而数量加法遵循的是四则运算法则。

由此类推平行四边形法则......

(设计意图：让学生进一步从概念中凝练，找出概念的本质属性，让数学概念通俗易懂，切忌死记硬背、生搬硬套。)

5 概念学习中应注意的一些问题

人类对数学概念的认识具有“渐进性”，学生对数学概念的认识要“重演人类认识数学概念的过程”，数学概念的抽象性决定了对它认识的曲折性，不可能一步到位，需要循序渐进、在已有知识经验的基础上进行再概括。教师要以学生为主体，学生的发展水平出发，积极让学生参与到概念探索的情境中来，举例辨析，对概念的内涵进行深度加工更准确的把握概念的细节，在概念的系统中学习概念，即要通过概念的应用，形成用概念作判断的“操作步骤”的同时，建立相关概念的联系，这是一次新的概括过程[3]。

[1]邵光华，章建跃.数学概念的分类、特征及其教学探索[J].课程·教材·教法，2009，29(7)：47-51.

[2]裘红明，吴道春，等.数学概念学习探究[J].成都大学学报：教育科学版，2008，22(5)：70-72.

[3]徐同，翟士杰.高中数学概念浅议[J].当代教育科学，2015，(6)：61-62.

The Analysis of Mathematics Concept Teaching from the Perspective of Student’s Concept Learning Process

CHANG Ning, WANG Shou-zhe, HAN Hua-rong

(College of Education Science, Kashgar University, Kashgar Xingjiang 844000, China)

Mathematical concepts play an essential role in mathematics teaching and learning. This paper attempts to begin with the concept formation and assimilation, provide teaching method in aspects of student’s cognitive structure, knowledge experience and abstraction, and make students grasp the essence of mathematics concept. This paper will also explain related issues with in a case study.

mathematical concepts; concept learning; concept teaching

2016-05-15

常 宁(1991-)，男，黑龙江佳木斯人，硕士研究生，研究方向为课程与教学论(数学)。

王守哲(1991-)，女，黑龙江勃利人，硕士研究生，研究方向为数学课程与教学论。

G642

A

1674-344X(2016)08-0117-04