基于稀疏分解的LFM回波信号检测算法

肖正安

(湖北第二师范学院 物理与机电工程学院，武汉 430205)



基于稀疏分解的LFM回波信号检测算法

肖正安

(湖北第二师范学院 物理与机电工程学院，武汉 430205)

针对低信噪比的雷达弱信号处理问题，基于稀疏分解理论，结合FOA优化算法，提出基于稀疏分解的LFM回波信号检测算法。首先建立雷达信号模型，得到回波模型和发射信号的关系，根据LFM回波信号特性构造过完备原子库；然后基于FOA算法实现雷达回波信号的稀疏分解，并将处理结果与常用的匹配滤波方法进行比较。仿真结果表明，本文算法不仅能精确重构出原始回波信号，而且在超低信噪比LFM信号处理时较匹配滤波方法具有明显的优势。

稀疏分解； 线性调频； 匹配滤波； FOA

1 引言

现代雷达系统概括来讲一般都包含信号处理和数据处理这两大重要组成部分。从对雷达回波信号处理的层次来讲，通常被看作对雷达探测信息的一次处理，目的是在杂波、噪声以及各种有源、无源干扰背景中提取有用的目标信息。而雷达数据处理通常被看作对雷达信息的二次处理，由于存在各种噪声和干扰，尤其随着隐身技术的发展和各种小目标的出现，使得目标回波信号越来越弱，因此，弱回波信号检测及处理问题成为雷达信号处理领域的热点及难点问题。目前，大部分传统的处理方法如基于匹配滤波的方法、分数阶傅里叶变换方法和小波变换方法[1-2]，这些方法不仅耗时长，数据量大，而且对超低信噪比信号几乎无能为力。

文献[3]于1993年提出了基于过完备原子库对信号进行稀疏分解的思想，开创了利用稀疏分解对信号进行分析这一新方向。由于信号的稀疏表示能在一定程度上自然地贴近信号的本质特征，因此受到了研究者的广泛关注，并且在很多领域都得到了重要的应用，如谱估计、波达方向估计、语音信号处理、雷达成像、雷达信号处理和盲源分离等[4-6]。在雷达信号处理方面的研究主要包括信号压缩和重构、阵列信号处理、目标分类和识别等。文献[7-8]均在离散余弦变换(Discrete cosine transform,DCT)字典下进行信号的稀疏分解，进而实现含噪声信号的稀疏重构以及目标的分类识别；文献[9]采用回波训练样本集作为字典实现水下底质回波的分类；文献[10]采用声矢量阵方向向量的形式建立原子库，构造出相应的稀疏向量，进而实现声矢量阵的波达方向(Direction of arrival,DOA)估计。

综上所述，实现信号稀疏表示的关键是如何构造过完备原子库以及如何从原子库中选取最优原子来表示信号。考虑待分解信号的形成原理，将先验信息融入过完备原子库的构造能够极大提高信号处理方法的效率。基于此，本文针对LFM回波信号数学模型，构建过完备原子库，并结合FOA优化算法方法快速搜索最优原子，提出基于稀疏分解的LFM回波信号检测算法，解决了信噪比很低的弱信号处理问题，并将处理结果与常用的匹配滤波方法进行对比分析，充分表明本文方法在处理超低信噪比信号的LFM回波信号具有很强的优势。

2 雷达工作原理及LFM信号

2.1 雷达工作原理

雷达(Radar)利用无线电波来检测目标并测定目标的位置，这也是雷达设备在最初阶段的功能。典型的雷达系统如图1，它主要由发射机，天线，接收机，数据处理，定时控制，显示等设备组成。利用雷达可以获知目标的有无，目标斜距，目标角位置，目标相对速度等。现代高分辨雷达扩展了原始雷达概念，使它具有对运动目标(飞机，导弹等)和区域目标(地面等)成像和识别的能力。雷达的应用越来越广泛。

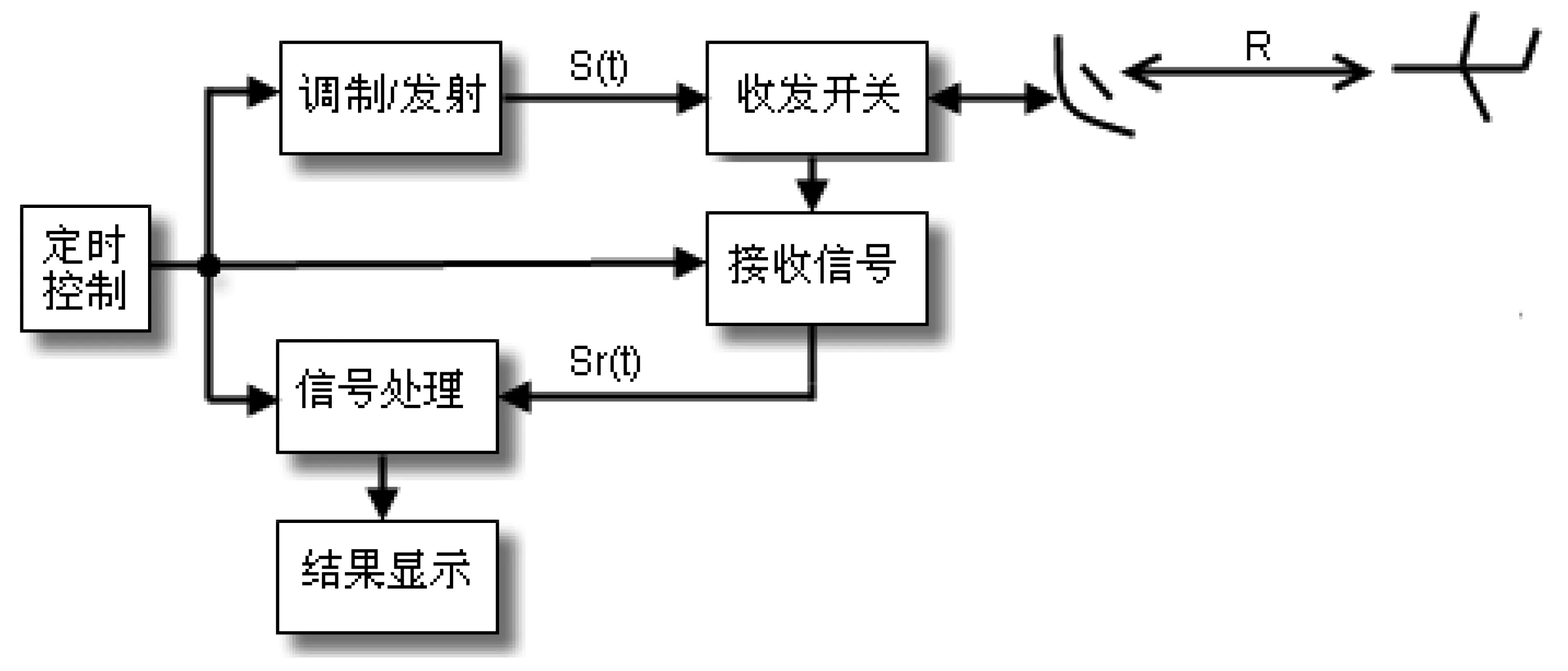
图1 简单脉冲雷达系统框图

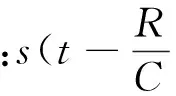
如果将雷达天线和目标看作一个LTI(线性时不变)系统则LTI系统的冲击响应可写成:

(1.1)

M表示目标的个数，σi是目标散射特性，τi是光速在雷达与目标之间往返一次的时间，

(1.2)

式中，Ri为第i个目标与雷达的相对距离。雷达发射信号s(t)经过该LTI系统，得输出信号(即雷达的回波信号)sr(t)：

(1.3)

2.2 线性调频(LFM)信号

脉冲压缩雷达最常见的调制信号是线性调频(Linear Frequency Modulation)信号, LFM信号(也称Chirp信号)的数学表达式为：

(2.1)

(2.2)

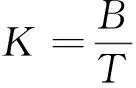
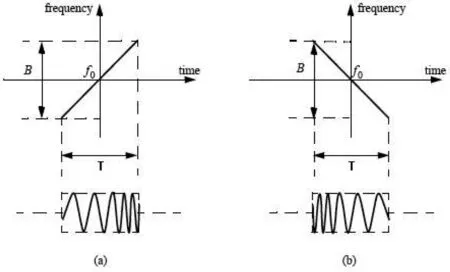
图2 典型的chirp信号(a)up-chirp(K>0)(b)down-chirp(K<0)

将2.1式中的up-chirp信号重写为：

s(t)=S(t)ej2πfct

(2.3)

式中，

(2.4)

是信号s(t)的复包络。由傅立叶变换性质，S(t)与s(t)具有相同的幅频特性，只是中心频率不同而以。

3 基于FOA算法的LFM回波信号稀疏分解

3.1 稀疏分解理论

稀疏分解的基(字典)是超完备的，是根据信号的特点构造超完备字典，从字典中搜索出与信号最近似的原子，用这些原子及其相应的分解系数近似(或精确)的表示待分解信号。稀疏分解的数学描述为

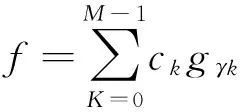
(3.1)

式中：f——待分解信号，gγk——超完备字典Λ={gr}r∈Γ中的一个原子，ck——解向量即信号与原子的内积。

对gγk要进行归一化处理，即‖gγk‖=1。首先将信号f分解为：

f=〈f,gr0〉gr0+R1f

(3.2)

其中，〈f,gr0〉gr0=c0是f对gr0的投影，R1f是信号的剩余量。可见R1f和gr0相互正交，于是：

‖f‖2=‖〈f,gr0〉‖2+‖R1f‖2

(3.3)

如果想使剩余量R1f最小化，就必须让投影〈f,gr0〉gr0=c0最大化。从信号空间角度出发，投影值最大化意味着原子达到最优匹配。然后采用(3.2)式对残余信号稀疏分解寻找第二个最优原子，依次迭代，完成(3.1)式的计算，信号的稀疏分解结束。

3.2 Fruit Fly Optimization Algorithm算法原理

和粒子群算法一样基于生物群体的觅食行为，学者Wen-Tsao Pan提出一种寻求全局最优解的新方法，实验结果表明该算法有更快的收敛速度。依照果蝇搜寻食物的特性，将Fruit Fly Optimization Algorithm算法归纳为以下几个必要的步骤：

1) 设定果蝇群体的大小，迭代次数，随机初始果蝇个体位置(x,y)。

2) 所有果蝇个体利用嗅觉搜寻食物的方向与距离，判断食物的味道浓度，浓度最大的 果蝇离食物距离最近，保留最佳味道浓度值及最佳位置。

3) 群体中的其他成员向最佳位置集中，并在该位置附近，所有成员展开随机搜索。

4) 群体所有成员在新位置判断食物的味道浓度。

5) 再次找出此果蝇群体的中味道浓度最高的果蝇(求极大值)，和前一次的最佳味道浓度值比较，如果浓度增大，保留该最佳味道浓度值及最佳位置，转到步骤3，如果浓度不变或减小，则转到步骤4。

6) 进入迭代寻优，重复执行步骤2-5。

3.3 LFM回波信号稀疏分解

具体算法如下：

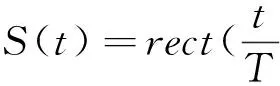
初始化 残余信号R1f=f(t)，迭代次数k=0，ck=0。

步骤1 计算残余信号与原子模型的内积ck；

步骤2 基于FOA优化算法找到内积向量绝对值最大的参数，代入原子模型，对应的原子gγk为最佳匹配原子；

步骤3 更新残差信号R1f=R1f-ckgrk；

步骤4 如果满足迭代终止条件，则输出相应的估计值；否则k=k+1，转到步骤1继续执行；

输出 信号分解系数ck，最优原子集合gγk，残差信号。估计值表达式为

(3.4)

4 计算机仿真及分析

对以下雷达系统仿真，雷达回波信号幅度RCS=[0.6 0.7 0.8 0.9 0.4 0.55]，信号波形为线性调频信号，频带宽度30兆赫兹(30MHz)，脉冲宽度10微秒(10us)，中心频率1GHz(109Hz)；；距离门10Km～15Km；目标Tar1：10.5Km，Tar2：11Km，Tar3：12Km，Tar4：12Km+5m，Tar5：13Km，Tar6：13Km+2m；取样频率150 MHz；噪声为高斯白噪声，信噪比SNR分别等于-3db、-6db及-10db。

根据2.2节的LFM数学模型，通过对回波信号稀疏分解并以少量原子进行稀疏重构，重构的回波信号与原始回波信号对比结果如图3所示。图4为对不含噪声信号分解后所剩余的残差信号。

从3、4图结果可以看出，本文提出的基于FOA算法的稀疏分解方法能够精确地重构出原始波形，而残差信号仅仅占信号总能量的0.27%。且对含噪声信号具有很好的去噪作用。

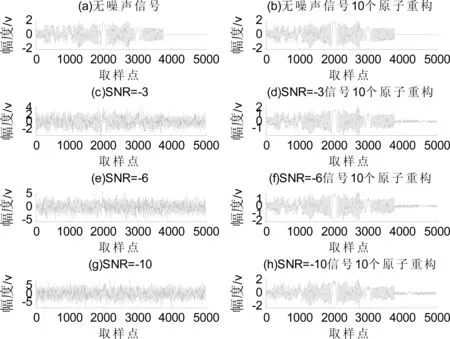
图3 源信号及稀疏重构信号

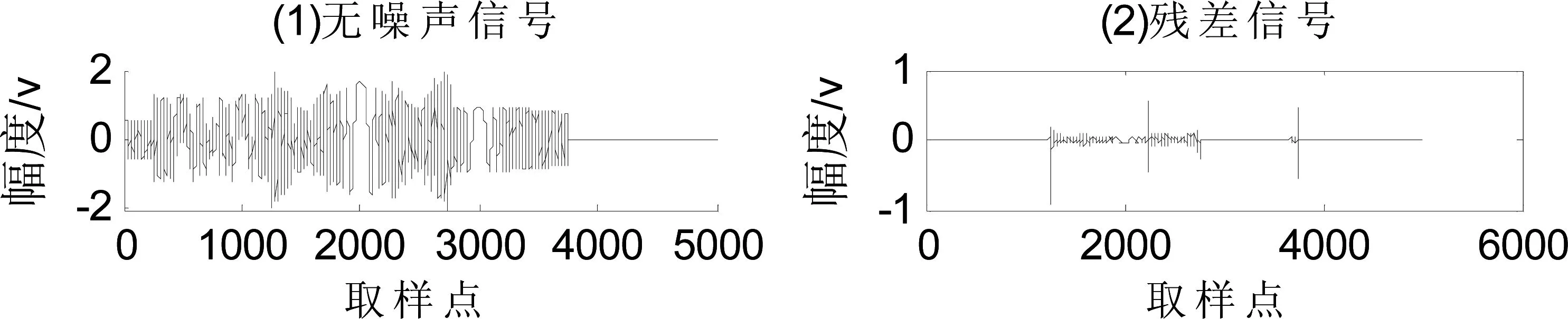
图4 源信号及残差信号

将稀疏分解前后的信号通过匹配滤波的结果如图5所示：

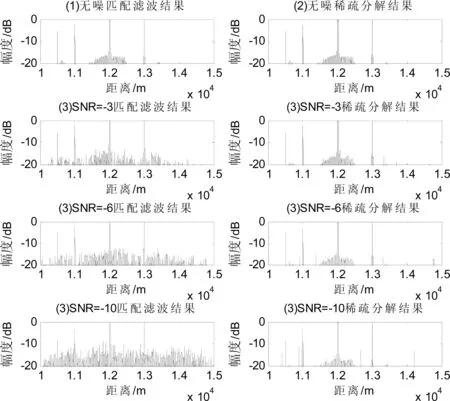
图5 稀疏分解前后匹配滤波结果

从图5中可以看出当信噪比时两种方法都能较好的获取目标特性；但是随着噪声的加强，直接匹配滤波获得的结果受到较强的干扰，而通过稀疏分解后获取的目标特性仍然非常清晰，充分说明本文算法是行之有效的且具备很高的可靠性。

5 结束语

本文针对雷达信号处理中的LFM弱回波信号中的问题，以稀疏分解理论为基础，考虑到LFM信号的特征及雷达的工作原理，设计了适合于该信号的原子模型，利用FOA算法强大的搜索能力，快速准确的找到最优原子的解，最终实现了超低信噪比下的雷达回波弱信号的稀疏分解，将处理后的结果进行匹配滤波，获取目标的特性。实验表明：本文方法能够准确的实现源信号的稀疏分解，分解后的残差信号仅仅占接收信号总能量的0.27%；当信噪比小于-6dB时，本文算法

也能得到较为精确的结论。稀疏分解后，结果表明：分解出来的前几个最大原子参数刚好和假设的6个目标一一对应，说明这些原子参数已经清楚的反映出目标信号的特征，并不需要再进行匹配滤波，本文之所以再滤波，目的是要和直接匹配滤波进行比较，通过比较说明本文算法是合理有效的。

[1]唐建锋，张登玉，罗湘南.一种基于多尺度小波变换的自适应滤波新算法[J].通信技术，2008,41(12):415-417.

[2]陈星，杜雨洺.一种基于匹配滤波的脉压新算法研究[J].通信技术，2013,46(4):133-138.

[3]Mallat S,Zhang Z. Matching pursuit with time-frequency dietionaries[J]. IEEE Transactions on Signal Processing, 1993,41(12):3397-3415.

[4]张弓，杨萌，张劲东，等.压缩感知在雷达目标探测与识别中的研究进展[J].数据采集与处理，2012,27(1):1-12.

[5]肖正安. 语音信号稀疏分解的FOA实现[J] 计算机工程与应用,2013,49(10):232-234.

[6]李越雷，张天骐，代少升，等.基于稀疏分解的微弱多分量LFM 信号参数估计[J].数据采集与处理，2009,24(2):161-166.

[7]肖正安，罗海峰.FOA-LM 算法及其在语音信号稀疏分解中的应用[J]. 计算机工程与应用,2015,51(12):219-222.

[8]Sabna N,Supriya M H,Pillai P R.Computationally efficient sparse reconstruction of underwater signals[J].Ocean Electronics,2013:88-95.

[9]杨勃，卜英勇，赵海鸣.基于信号稀疏分解的水下回波分类[J].声学学报，2010,35(6):608-614.

[10]付金山.基于稀疏分解理论的声矢量阵信号处理[D].哈尔滨：哈尔滨工程大学，2012.

LFM Echo Signal Detection Algorithm Based on Sparse Decomposition

XIAO Zheng-an

(School of Physics and Mechanical and Electrical Engineering, Hubei University of Education,>Wuhan 430205, China)

For ultra-low-SNR linear frequency modulation echo signal processing problem, an LFM echo signal detection algorithm is presented based on the theory of sparse decomposition and the Fruit Fly Optimization Algorithm. First, the LFM signal model of Radar echo signal is established, the relation between the echo signal and incident signal is obtained, and the over complete dictionary fitting for LFM echo signal characteristics is structured. Furthermore, the sparse decomposition of LFM echo signal is conducted based on the Fruit Fly Optimization Algorithm, and the processing results are compared and analyzed with the commonly used matched filter methods. The simulation results show that the proposed method can accurately reconstruct the original echo signal, and has obvious advantage in processing LFM echo signal with ultra-low SNR.

sparse decomposition; linear frequency modulation; matched filter; FOAL Fruit Fly Optimization Algorithm

2016-06-08

湖北省教育厅指导性项目(B2015025)

肖正安(1974-)，男，湖北钟祥人，讲师，硕士，研究方向为数字信号处理。

TN911.73

A

1674-344X(2016)08-0008-04