城市轨道交通网络的同步换乘模型研究

何南,孟可欣,张美娇,冯冬生,唐华,董杰

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*



城市轨道交通网络的同步换乘模型研究

何南,孟可欣,张美娇,冯冬生,唐华,董杰

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

为了增加轨道交通吸引力，提高乘客换乘效率，构建城市轨道交通网络的同步换乘数学模型，以协调优化换乘时间解决同步换乘问题.该模型通过不断确定换乘节点，调整发车间隔，增加相遇次数，获得同步换乘次数最大化的发车时刻表，以达到优化列车运行的目的.在研究过程中，选取上海市进行实证分析，基于数据收集和模型构建，对轨道交通网络中2，7，8号地铁线路的运行时间进行优化调整.与现实地铁运行图相比，在30 min时间内，增加3次同步换乘，提高地铁运行效率，减少乘客的等待时间，节约成本，同时将对规划、建设、运营、管理城市轨道交通起到重要指导意义.

城市轨道交通；同步换乘；换乘时间；发车时刻表

0 引言

随着经济的快速发展，城市化进程不断推进，交通需求和交通供给之间的矛盾逐渐成为世界各地面临的最大矛盾.根据国外城市的发展经验，大力发展公共交通是缓解这种矛盾的最好方法.城市轨道交通在公共交通中占绝大比例[1]，其交通网络的形成增加了各线路之间的紧密联系.与此同时换乘站作为线路的连接点，聚集了大量客流，地铁线路间的换乘距离也相对较远，如何提高换乘服务质量和改善换乘效率成为影响轨道交通发展的重要因素.综上所述，城市轨道网络中同步换乘模型研究可以完善换乘体制，协调客车到达换乘站的时间，达到无缝换乘的最终目标，也可以合理有效的分配交通资源.

城市化的飞速发展，带动轨道交通的大跨步进展.专家学者们结合国内实际情况，改善轨道交通网络.通过对国内轨道交通线路的研究，罗雁云[2]主要对提高换乘效率问题进行研究，从而对轨道交通同步换乘进行优化；张铭[3]等人从宏观和微观两个层面进行探索，对整个交通网络中的换乘节点进行了优化；周艳芳[4]等人建立了换乘同步性优化模型和发车时间优化模型.

国外的专家学者对于该问题也有深刻的研究，并取得一定成果.在研究过程中，他们更注重时效性，如Schoiifeld和Lee[5]、Fung和Yuen[6]等人主要就换乘站所衔接线路的发车时间进行优化；Corey[7]、Dhingra[8]等人则建立城市轨道交通的换乘协调优化模型和列车等待效益最大化模型.

经过国内外研究者的不懈努力，换乘站换乘问题已经取得一定成果.主要通过列车发车间隔、同步换乘次数等方面的定量调整优化来缩短乘客的换乘等待时间或降低用户和运营者的广义费用.我们在学者相关研究的基础上，构建同步换乘模型，针对具体的地铁线路进行设计，运用启发式算法调整发车时间，优化同步换乘次数.本文选择上海地铁进行实证研究.基于一定的假设条件，以同步换乘最大化为目标建立同步换乘模型，通过协调发车时间，逐步优化同步换乘.

1 同步换乘模型算法研究

为了解决乘客在地铁站等待换乘时间过长的问题，依据Ceder的相关研究[9]建立同步换乘模型以实现地铁线路间无缝链接的目的.模型基于特定的轨道网络，它由线路和节点两个要素组成.其中网络所包含的节点数不得小于1，线路从起始点到网络中某一节点的走行时间不得小于0.以两条线路上的车辆同步到达次数达到最大化为目标构建函数，其数学表达式为：

(1)

约束条件为：

X1k≤Hmaxk,1≤k≤M

(2)

(3)

Hmink≤X(i+1)k-Xik≤Hmaxk,

(4)

(5)

式中,T为循环时间(出发时间在区间[0，T])；M为网络中线路的数目；N为网络中节点的数目；Hmink为最小发车间隔时间；Hmaxk为最大发车间隔时间；Fk为在区间[0，T]内的发车数；Tkn为路径k上从起始点到节点n的走行时间；Tqn为路径k上从起始点到节点q的走行时间；Xik为线路k的第i辆车的发车时间;线路k上的第i辆车可以与线路q上的第j辆车在节点n处相遇则Zikjqn=1，否则为0.

基于模型构成，结合启发式算法，应用图1步骤，逐步确定线路发车时间及换乘节点，最终达到优化换乘，节约时间的目的.对NO节点： ①至少

图1 模型算法流程图

有一条线路穿过该节点，且对于这条线路来说，不是所有车辆的出发时间都已被确定；②在这个节点上能够实现更多的同步到达.新节点：如果一个节点还没有确定到达时间.不可能节点：如果没有更多的同步到达车辆在这个节点到达.

其步骤为：

步骤1：初始化.检查问题是否可行.若可行，则设置数据结构，并标记所有可能节点.数据结构包括：①每条运输线路i，其包括最小发车间隔，最大发车间隔，发车数，每条线路经过的节点个数四个要素;②节点n，其包括通过该节点的路线的数量及到达每个节点的运行时间最大的线路两个要素.

步骤2：从可能的节点中选择一个节点NO.选择NO节点依据为：不同车辆同时到达该节点的次数最大；通过该节点的线路最多；起点到该节点的运行时间最少.

步骤3：如果NO是新的节点，则执行First部分，否则执行MIDDLE部分.

FIRST部分是确定经过该节点的车辆出发时间，从而使车辆能尽早到达该节点，然后根据线路的最小发车间隔，最大发车间隔继续确定同步到达节点.MIDDLE部分尝试对通过这些线路的车辆设置出发时间，使得这些列车可以在已经被设定的到达时间里最早到达节点.

步骤4：如果有任何可能节点，转到步骤2;如果有更多路线，执行CHOOSE并转到步骤2；否则转到步骤5.

CHOOSE部分测试是否有更多节点可能实现同步到达，或找到没有全部设置出发时间的线路.在这种情况下，选择穿过节点数目最多的线路，依据最后发车时间的不同最小发车间隔来设定出发时间.以这种方式，设置额外可能到达车辆最多的节点.通过线路i的所有节点被标记为可能节点，并且该过程返回步骤2.确定所有线路上车辆的发车时间.

步骤5：考虑乘客的换乘走行时间(C).在所有线路中选定一条客流最多的线路为主要线路，将其他线路上车辆的发车时间都减去该线路至主要线路的乘客换乘走行时间，确定最终发车时间，结束.

2 实证分析

上海市作为一个国际大都市，其经济发展迅猛，交通运输四通八达，城市轨道交通网络建设完善.截至2014年12月28日，上海轨道交通共开通线路14条(1-13号线、16号线)，全网运营线路总长548公里，车站337座.在2015～2020年规划中，有5条线路延伸规划、4条线路新建计划.

根据上述模型构建和算法流程，选取上海地铁2号线，7号线和8号线为例，计算其发车时间.图2为上海地铁线路图.

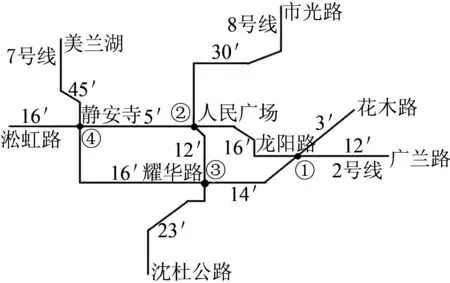
图2 上海市地铁2号线、7号线和8号线线路图

从图2所示的线路图可以看出，这三条线路连接着上海的各个方向，对上海的轨道交通运输，起着重要作用.图2中的各线路上的走行时间均是实际距离与车辆行驶速度的比值，并规定由东到西，由南到北为上行.由于车辆在每个站停留时间的长短是由运行图所规定的，每条线路上的车辆在同一地点的停留时间是相同的.因此若考虑停留时间，则每条线路上的发车时间都是同步变化的.为了方便计算，我们将停留时间加到走行时间里，来优化发车时间.

表1为根据调查得出的2,7,8号线路的上下行发车情况.

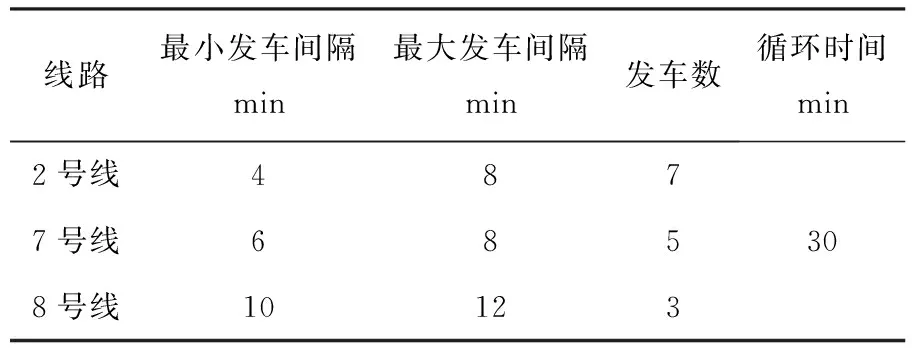
表1 发车情况表

根据表1给出的发车时间间隔和发车数等数据进行计算，计算发车时间.

上行列车发车时间具体的计算过程如下：

步骤1：由线路结构数据可知，2号线通过节点1，2，4；7号线通过节点1，3，4；8号线通过节点2，3.所有节点均有2条线路通过.

步骤2：所有路线在各节点间的最大行驶时间分别是12，35，23和33 min，最低是12 min，所以NO=1.

步骤3：执行FIRST.在节点1第一次相交的时间为10 min，因此，2号线和7号线的发车时间分别为0和9 min.

步骤4：有更多可能的节点，因此返回到步骤2.

步骤2：在节点1，2，3和4号到达车辆的数量分别是1，1，1和2，因此NO=4.

步骤3：执行MIDDLE，计算得相遇时间为42min，2号线的发车时间为第9 min.

步骤4：有更多可能的节点.

步骤2，3：执行MIDDLE，选择节点2，在节点2的相遇时间为第37 min，8号线的发车时间为第2 min.

步骤4，5：无更多可能的节点.执行CHOOSE，安排2号线发车时间为第4 min；7号线为第3 min；8号线为第12 min.

步骤4：有更多可能的节点.

步骤2，3：执行MIDDLE，选择节点2，在节点2的相遇时间为第47 min，由此确定2号线的发车时间为第19 min.

步骤2，3：执行MIDDLE，选择节点1，在节点1的相遇时间为第31 min，由此确定7号线的发车时间为第28 min.

步骤2，3：执行MIDDLE，选择节点3，在节点3的相遇时间为第45 min，由此确定8号线的发车时间为第22 min.

步骤2，3：执行MIDDLE，选择节点4，在节点4的相遇时间为第61 min，由此确定2号线的发车时间为第28 min.

步骤4，5：无更多的可能的节点.执行CHOOSE，安排2号线发车时间为第13 min.

步骤2，3：执行MIDDLE，选择节点1，在节点1的相遇时间为第25 min，由此确定7号线的发车时间为第22 min.

步骤4，5：无更多的可能的节点.执行CHOOSE，安排7号线发车时间为第15 min，2号线的发车时间为第23 min.

计算得出的上行方向发车时间表如表2所示.

表2 上行方向发车时间表 min

考虑到乘客在换乘时的走行时间，各线路的发车时间需要调整.由于2号线的客流量最大，因此我们选择2号线为主要线路，其他线路配合该线路进行调整，以此实现同步换乘的目的.

其中在每个换乘点的换乘走行时间如表3所示.

表3 换乘走行时间表 min

结合表2和表3所示数据，以2号线为主要线路，7、8号线为次要线路，其中主要线路上发车时间不变，把换乘走行时间融入到次要线路发车时间，根据次要线路上的最小发车间隔时间和最大发车间隔时间，对其线路上的发车时间进行优化调整，保证乘客可以及时到达主要线路上的乘车位置.调整后的上行发车时间表如表4所示.

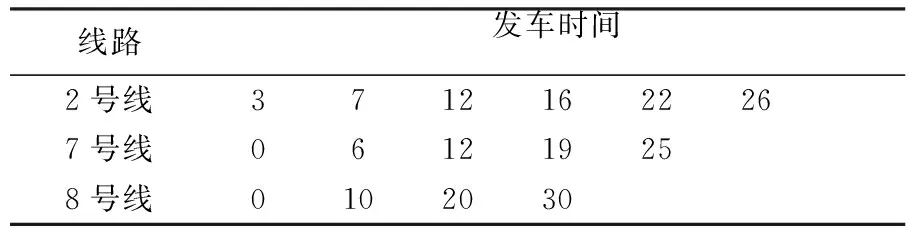
表4 调整后的上行发车时间表 min

通过实证研究，我们为上海地铁2,7,8号线优化出30 min之内的列车时刻表，改进原有的发车时间和发车间隔，其中2号线开行6辆列车，7号线开行5辆列车，8号线开行4辆列车，同步换乘次数增加3次，切实有效地减少运营成本，增强轨道交通的高效性，吸引更多的人乘坐地铁，增加乘客出行的满意度.

3 结论

本文基于一定的条件假设对地铁同步换乘问题进行数学建模，并采用启发式算法对复杂的模型进行求解，从而得到更优的发车时刻表.结果表明，应用此法优化后的列车时刻表，具有更多的同步换乘次数.通过实证研究说明优化方法的可行性，优化上海地铁线路的同步换乘，解决发车间隔过长，换乘方式复杂等问题，大大缩短乘客的等待时间，提高乘客满意度.目前，城市轨道交通飞速发展，绝大多数城市兴建地铁作为主要的运输方式.预计使用此法，可以有效地提高运营的整体效率，为人们的出行带来便利.

[1]张迅. 基于换乘协调的城市轨道交通换乘站列车衔接优化研究[D].北京:北京交通大学，2014.

[2]罗雁云,董国鹏,陈薇萍.关于城市轨道交通换乘的几点思考[J].城市轨道交通研究,2004(6):14-16.

[3]张铭,徐瑞华.轨道交通网络列车衔接组织的递阶协调优化[J].系统工程,2007(9)：33-37.

[4]袁振洲,曹志超. 结合列车时间表的地铁换乘同步性优化[J].现代城市轨道交通,2014(6):14-16.

[5]LEE K K T, SCHONFELD P. Optimal slack time for timed transfers at a transit terminal [J]. Journal of Advanced Transportation, 1991, 25(3):281-308.

[6]YUEN T W Y, FUNG ICW. Optimizing Timetable Synchronization for Rail Mass Transit [D]. Planning and Development Department, MTR Corporation Limited, Hong Kong,2008.

[7]COREY J WONG. Improving the Network Performance of Urban Transit Systems [D]. Berkeley:University of California, 1997.

[8]VERMA A , DHINGRA S L. Developing Integrated Schedules for Urban Rail and Feeder Bus Operation[J].Journal of Urban Planning and Development,2006,132(3): 138-146.

[9]CEDER AVISHAI. Public Transit Planning and Operation: Theory,Modeling and Practice [M]. Oxford: Elsevier, 2007: 140-154.

Research on Synchronous Transfer Model of Urban Rail Transit Network

HE Nan, MENG Kexin, ZHANG Meijiao, FENG Dongsheng, TANG Hua, DONG Jie

(School of Traffic and Transportation Engineering,Dalian Jiaotong University, Dalian 116028，China)

A synchronous transfer model of urban rail transit network is established to increase the attraction of public transportation and improve the transfer efficiency of passengers. Transfer time is optimized, and the problem of synchronous transfer is solvesd. This model achieves the purpose of train operation optimization by getting the maximum number of simultaneous transfer time. It can determine the transfer station continually, adjust the departure interval and increase the number of encounters. In the study, based on a model formation and data collection of Shanghai, the running time among the subway lines 2, 7 and 8 is adjusted and optimized. Compared with the actual metro running chart, it increases three synchronous transfer times and improves running efficiency by 30 minutes. This model reduces the passenger waiting time, saves costs and improves operational efficiency. The usage of synchronous transfer model can play an important guiding to planning, construction, operation and management of urban rail transportation.

urban rail transit; synchronous transfer; transfer time; departure timetable

1673-9590(2016)04-0001-04

2015-10-10

何南(1985-),女,讲师,博士,主要从事交通系统工程的相关的研究E-mail:honny_he@hotmail.com.

A