考虑移动荷载随机性的裂纹梁动响应分析与裂纹定位

赵明杰， 尹 涛， 傅少君

考虑移动荷载随机性的裂纹梁动响应分析与裂纹定位

赵明杰， 尹 涛， 傅少君

（武汉大学 土木建筑工程学院，湖北 武汉 430072）

对简支裂纹梁在移动随机荷载作用下的位移响应及裂纹定位问题进行研究。发展了含横向开口裂纹的Euler-Bernoulli梁在单个匀速移动随机荷载作用下位移响应理论解，研究了移动荷载噪声标准差恒定情形下裂纹梁的随机动力响应问题，并采用Monte Carlo数值模拟法对提出的移动随机荷载作用下裂纹梁位移响应理论解的正确性进行验证。此外，提出了一种基于时-空转换的梁结构损伤统计定位方法，利用移动荷载的匀速性，将有限测点传感器采集的时域随机响应信号分别转换为梁结构的空间域随机响应，利用Daubechies离散小波变换揭示裂纹引起的空间域响应曲线突变可识别性与随机荷载噪声程度之间的关系，并通过一系列不同速度随机移动荷载下裂纹梁的空间域响应及其均值的离散小波变换分析，实现随机荷载噪声情况下的裂纹定位。

移动随机荷载； Monte Carlo模拟法； 时-空转换； 小波变换； 裂纹定位

随着国内外桥梁建设事业的快速发展，桥梁 结构在车辆移动荷载作用下的动力响应与安全运营问题日益受到关注。Fryba［1］研究了不同荷载作用下梁模型的位移响应规律。Michaltsos［2］分析了简支梁在质量块移动作用下的位移响应特性。Abu Hilal［3］基于Euler-Bernoulli梁理论研究了不同边界条件梁结构在移动荷载作用下的位移响应规律。以上研究主要考虑不同形式与大小移动荷载作用下梁结构的动力响应规律，未涉及损伤状态下梁结构的动力响应与损伤检测相关问题。

刘宇飞等［4］基于梁式结构的平均曲率模态分析，利用缺口平滑拟合技术及Newmark算法对移动荷载作用下梁结构局部损伤进行定位。Law和Lu［5］利用狄拉克函数模拟开口裂纹，发展了一种移动荷载作用下基于时域信号的梁结构损伤识别方法。赵俊等［6］基于小波分析方法对移动荷载作用下简支梁动态响应及裂纹识别进行了研究。由于桥面行车状况及车辆自身特性等原因，实际车辆移动荷载大小并非恒定，具有随机性，其会加大桥梁动力测量数据的不确定性，进而影响损伤检测结果，但以上研究均未考虑该随机荷载因素影响。尽管吕峰等［7］基于有限元理论的精细积分方法研究了移动随机荷载作用下桥梁结构动力响应问题，但精细积分格式的有限元法及类似数值方法在求解移动荷载动力问题尤其是随机动力学问题时计算量过大。因此，有必要开展考虑移动荷载随机性影响的含损伤梁结构随机动响应与损伤检测相关问题研究。

本文首先利用Duhamel积分法建立两端简支裂纹梁在匀速移动随机荷载作用下的理论解。基于断裂力学理论引入裂纹边界条件，研究了裂纹梁的随机位移响应，并探讨了随机荷载位移响应均值与其标准差的关系。其次，运用Monte Carlo数值模拟法验证了移动随机荷载作用下裂纹梁位移响应理论解的正确性。然后利用Daubechies离散小波变换方法［8］探讨了裂纹引起的位移响应突变可识别性与随机荷载响应噪声相对大小的关系问题。最后通过一系列不同速度移动随机荷载作用下裂纹梁给定测点位移响应小波变换分析以及位移响应均值的小波变换分析，验证了本文方法的正确性。

1 理论背景

本文研究的裂纹梁模型如图1所示，其中，设梁长为L，裂纹位于l1位置，边界条件设为两端简支，同时假设裂纹始终张开，且忽略裂纹尖端处的应力奇异。基于Euler-Bernoulli梁理论，完好梁的振动控制方程可表示为［1］：

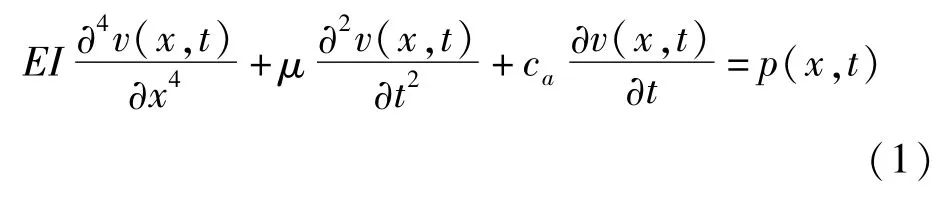
式中：EI为梁的抗弯刚度；μ为梁单位长度的质量；ca为梁的阻尼系数；v（x，t）表示梁任一点任意时刻的横向位移；p（x，t）为移动随机荷载，假定为一个随时间变化的集中力，并沿梁以恒定速度c移动（如图2），即

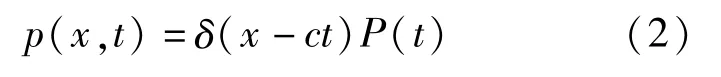
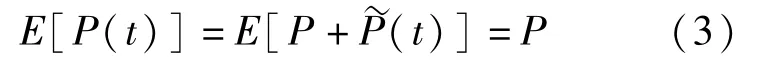
利用振型叠加法原理，振动控制方程（式（1））通解表示为：

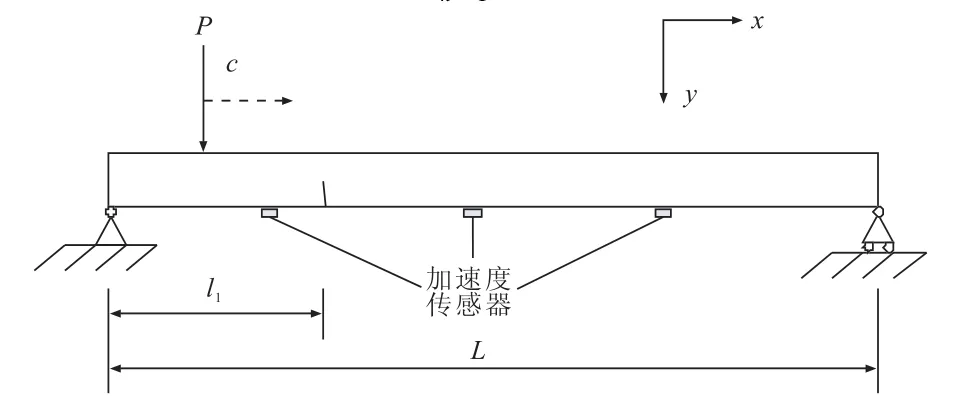
图1 移动随机荷载作用下的裂纹梁模型

图2 移动随机荷载［9］

式中，Yk（t）为模态振型上的量值；Xk（x）表示k阶模态下梁的模态振型，考虑裂纹影响，Xk（x）可分段表示为：

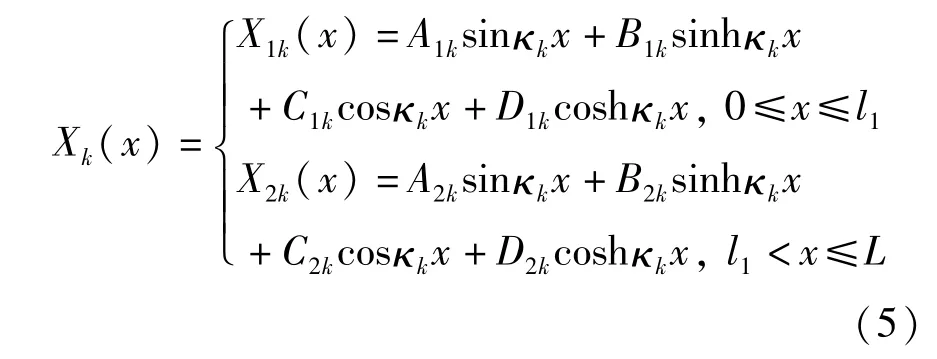
式中：A1k、B1k、C1k、D1k、A2k、B2k、C2k、D2k为待定系数，由边界条件及裂纹处连续条件共同确定；常数κk是梁的k阶频率参数。梁的边界条件及连续性条件为：

式中：Δ1为裂纹深度的无量纲参数［10］，表示为

式中：β1为裂纹相对深度，是裂纹深度与梁高比值，表示成β1=d/h，h为梁高，d为裂纹深度。

将式（4）与式（2）代入式（1），并利用模态正交性可得：

式中：Yk（t）、Y·k（t）、Y¨k（t）分别为模态振型上的量值及其一阶导数和二阶导数；ωk为k阶模态的自振圆频率；ξk为k阶模态的无量纲阻尼比；Qk（t）为k阶模态的广义力；mk为k阶模态的广义质量，分别表示为：

式中：t1、t2分别为荷载运动到裂纹处与梁端点处的时间，即，t1=l1/c，t2=L/c。用Duhamel积分方法求解公式（9）得：

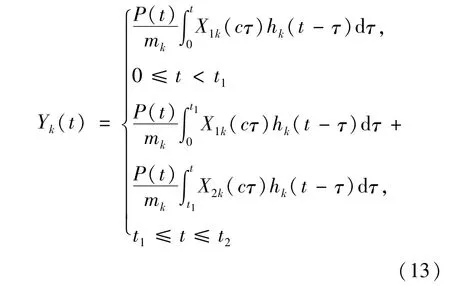
式中：hk（t）是脉冲响应函数，定义为：

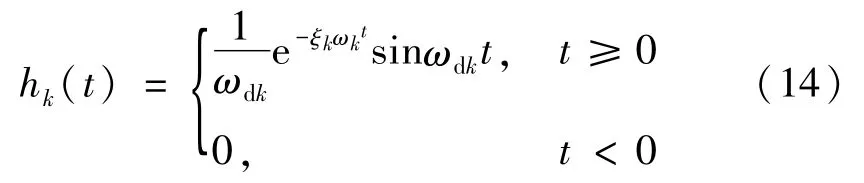
求解式（13），将结果代入式（4），再结合式（3）可得移动随机荷载作用下的挠度随机响应均值为：

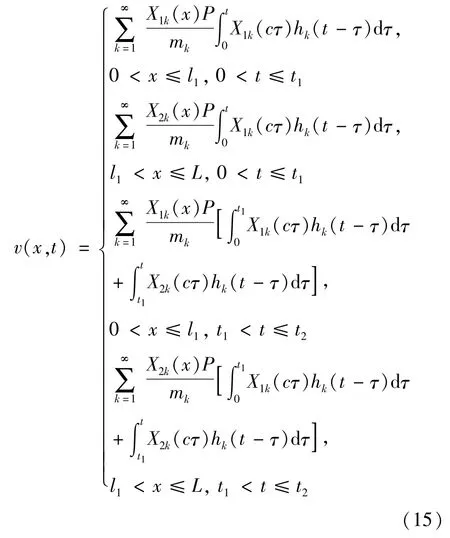
其中，

式中：

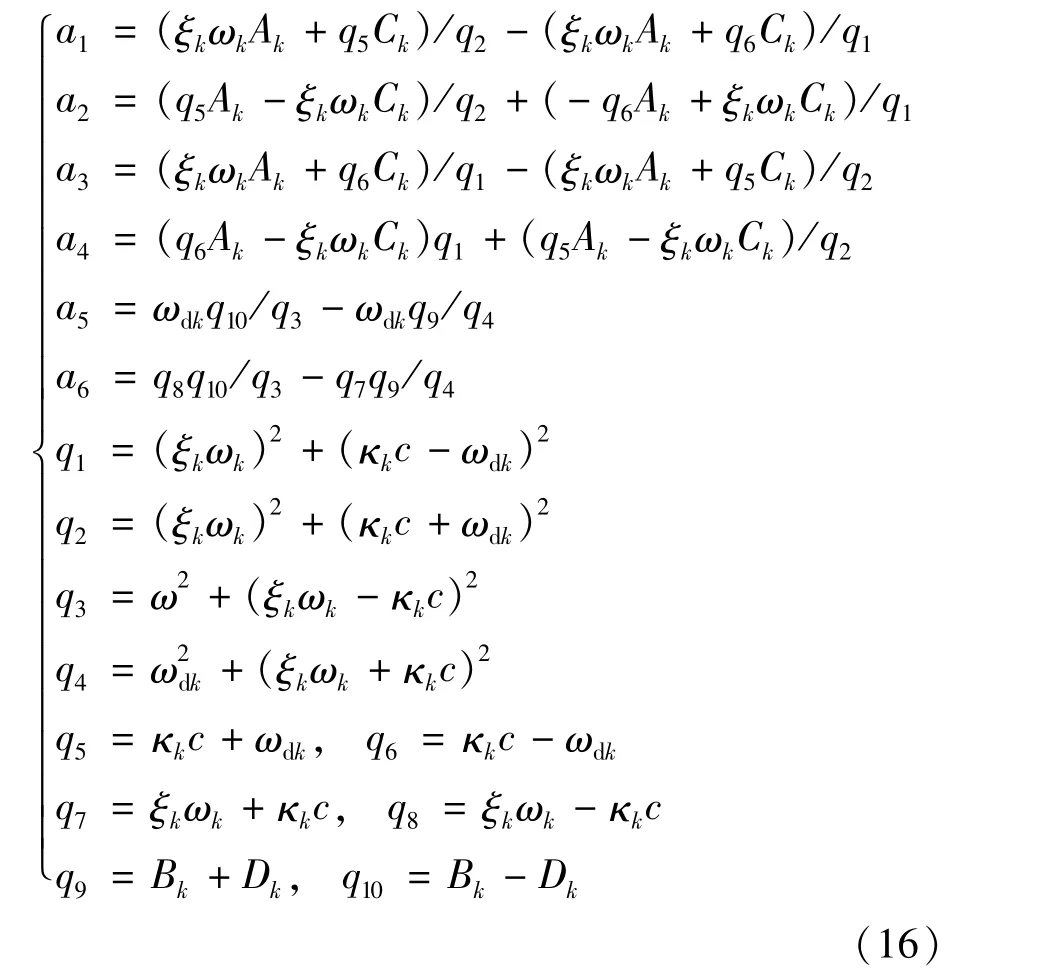
此外，移动随机荷载下的挠度随机响应的协方差Cvv可表示为：

其中，广义位移的协方差CYjYk可表示为：

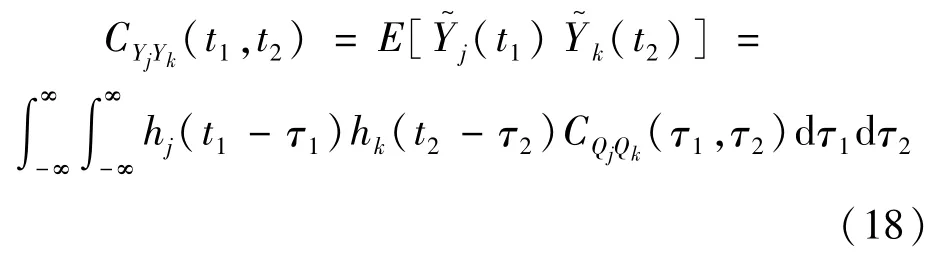
而广义力的协方差CQjQk可由荷载的协方差CPP计算得到：

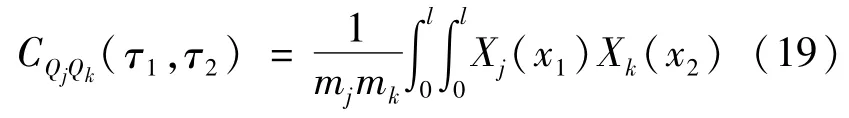
综合公式（11）、（13）、（17）、（18）和（19），移动随机荷载作用下裂纹梁挠度响应方差可分段表示为：

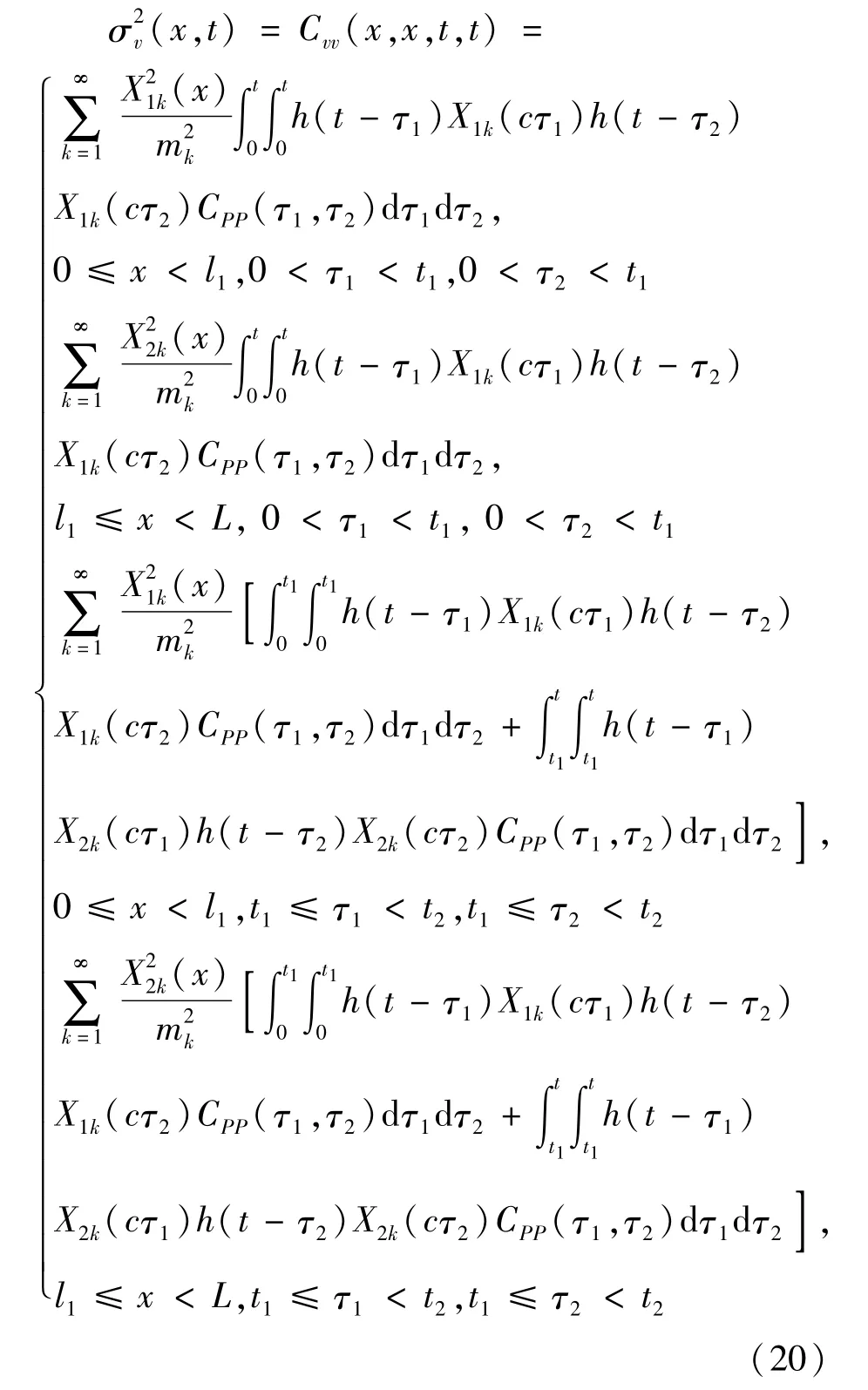
特别地，在荷载方差恒定情况下，即：

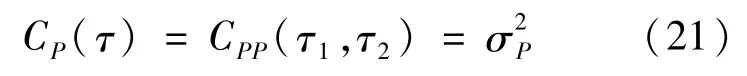
梁的位移响应方差可以由式（20）简化为

通过式（15）与（20）可以得出移动随机荷载作用下裂纹梁任意位置处挠度响应的统计特性。

2 数值仿真研究

2.1 移动随机荷载作用下裂纹梁的挠度响应

本节主要分析不同裂纹深度情况下，随机匀速荷载对简支梁位移响应的影响。为研究方便，引入无量纲时间参数s=t/t2，即当s=0时，荷载在梁的最左端；当s=1时，荷载在梁的最右端。裂纹梁的几何及材料特征参数见表1。

取荷载速度c分别为60、120、180、240 km/h，阻尼比取0.01，裂纹深度参数取0.4，裂纹位置为0.3L，荷载幅值为100 kN，图3比较了不同速度工况下裂纹梁跨中位置的无噪声挠度时程曲线，从图中可以看出不同速度下裂纹梁的挠度曲线形状上有所不同，而挠度峰值无太大区别。此外，在各种速度模式下，该图无法直接观察到裂纹的影响。

本节着重于研究某一速度的随机荷载作用下裂纹梁跨中挠度时程响应。取荷载速度c为60 km/h，荷载均值为100 kN，荷载噪声标准差分别为10 kN和20 kN，其他工况条件不变，可得裂纹梁移动随机荷载作用下的跨中挠度响应，如图4（其中，图例AD、SD分别代表响应均值与标准差）。

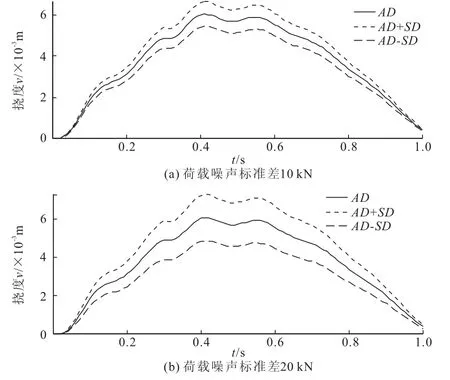
图4 不同荷载噪声标准差下随机荷载响应均值±标准差曲线

从图4中可以看出，恒定标准差情形下的移动荷载，其位移响应围绕平均值在一定范围内波动，且波动范围与荷载噪声标准差大小相关。

2.2 移动随机荷载作用下裂纹梁挠度响应的Monte Carlo法验证

假定随机荷载噪声在任意时刻都服从均值为100 kN、标准差为20 kN的正态分布。在该样本空间采集101个荷载点、共100组荷载，分别计算跨中测点挠度响应值。然后将各时刻挠度响应值的散点与挠度均值±标准差的位移响应图进行对比，如图5（图例RD代表Monte Carlo模拟的随机荷载响应点）。

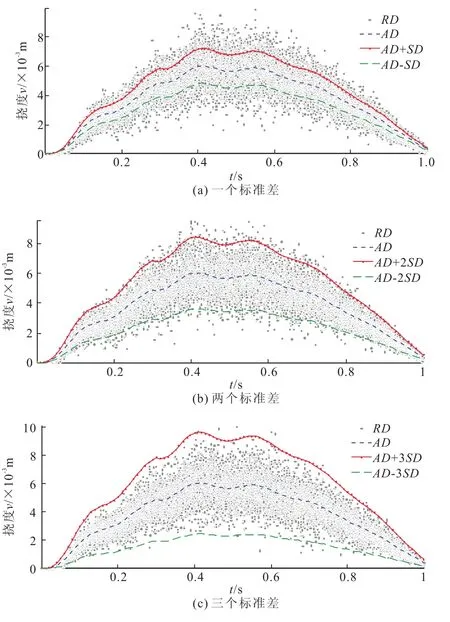
图5 随机荷载响应均值±不同标准差曲线与随机荷载响应点对比

从图5a中可以看出，在一个标准差范围内，位移响应的散点在中间处较密集，而在外端相对较疏散，且大多数散点都在挠度平均值±挠度标准差曲线之间（即红色点划线与绿色虚线之间）。经统计，约65%～75%的散点被上述曲线包围。根据正态分布规律，距平均值小于一个标准差范围内的数值约占全部的68%，可见图5a符合正态分布规律。类似地，通过对图5b与图5c Monte Carlo模拟结果的统计分析，可以得出距平均值小于两个与三个标准差范围内的数据分别约占全部的95%与99.5%，均服从正态分布规律。由此可见，本文理论分析方法与Monte Carlo数值模拟法结果吻合，正确性得到验证。

2.3 移动随机荷载作用下的梁裂纹检测

上节利用移动荷载的匀速性，将沿梁纵向布置的有限数量传感器测点（如图1）采集的时域响应信号分别转换为沿梁纵向的空间域响应，但前面分析表明裂纹造成的该空间域响应影响很小无法直接分辨（如图3），需要一种有效的信号分析手段以揭示裂纹导致局部信号奇变的空间位置。传统的快速傅里叶变换及其改进的短时傅里叶变换都因其自适应能力差、缺乏空间局部性而无法很好的分析信号，而通过引入多尺度分析法与正交小波基的小波变换在时域和频域中都具有良好的局部化性质，很好地解决了时间与频率分辨率的矛盾，有利于信号奇异检测。

本节通过引入离散Daubechies小波变换以揭示裂纹引起的空间域响应曲线突变位置而实现裂纹定位。众所周知，基于小波变换的裂纹检测方法受噪声的影响较大，本节在考虑移动荷载随机性引起的动响应随机性条件下，结合本文具体算例，从噪声水平及梁结构损伤程度两者相对大小出发，定性阐述了两者对小波变换检测结果的影响。取荷载速度c为60 km/h，裂纹位置为0.3L，裂纹相对深度δ为0.4，荷载噪声标准差为10 N，计算裂纹梁跨中测点在随机荷载作用下的位移响应曲线，如图6所示，很明显该图无法直接分辨裂纹对荷载响应时程曲线的影响。为揭示图6中裂纹位置，结合Daubechies小波变换，图7给出了裂纹梁跨中测点挠度时程曲线于不同尺度下的小波变换结果。经比较，db2小波和db3小波相对于其他尺度小波在裂纹处的突变更明显，本文以下分析选db2小波进行。裂纹位置保持0.3L，裂纹相对深度分别取0.2、0.4、0.6，而荷载噪声标准差分别采用10、200、1000 N，然后对裂纹梁跨中位置的挠度响应曲线进行小波分析，结果如图8所示。

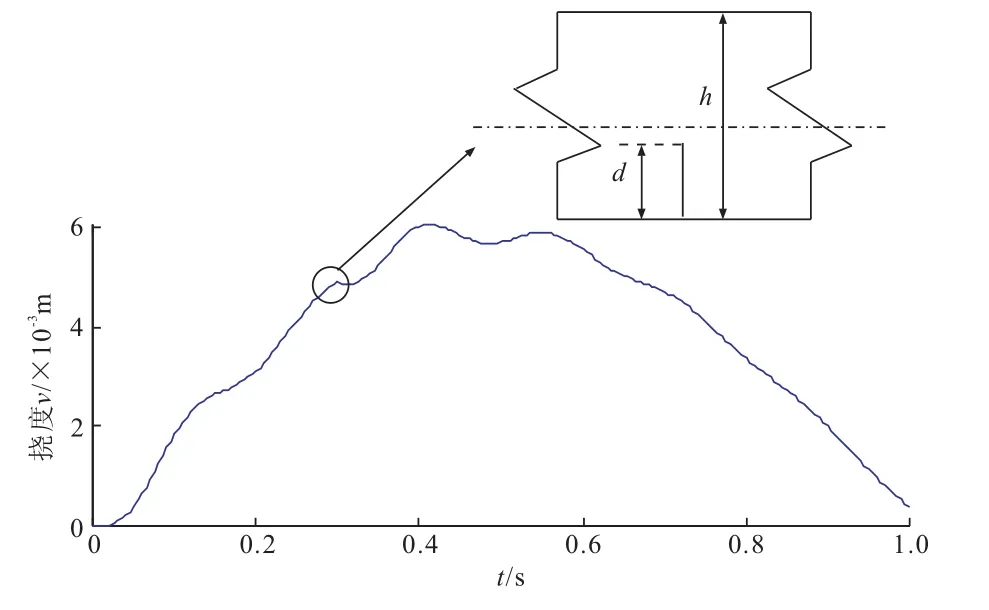
图6 移动随机荷载作用下裂纹梁跨中测点挠度时程曲线

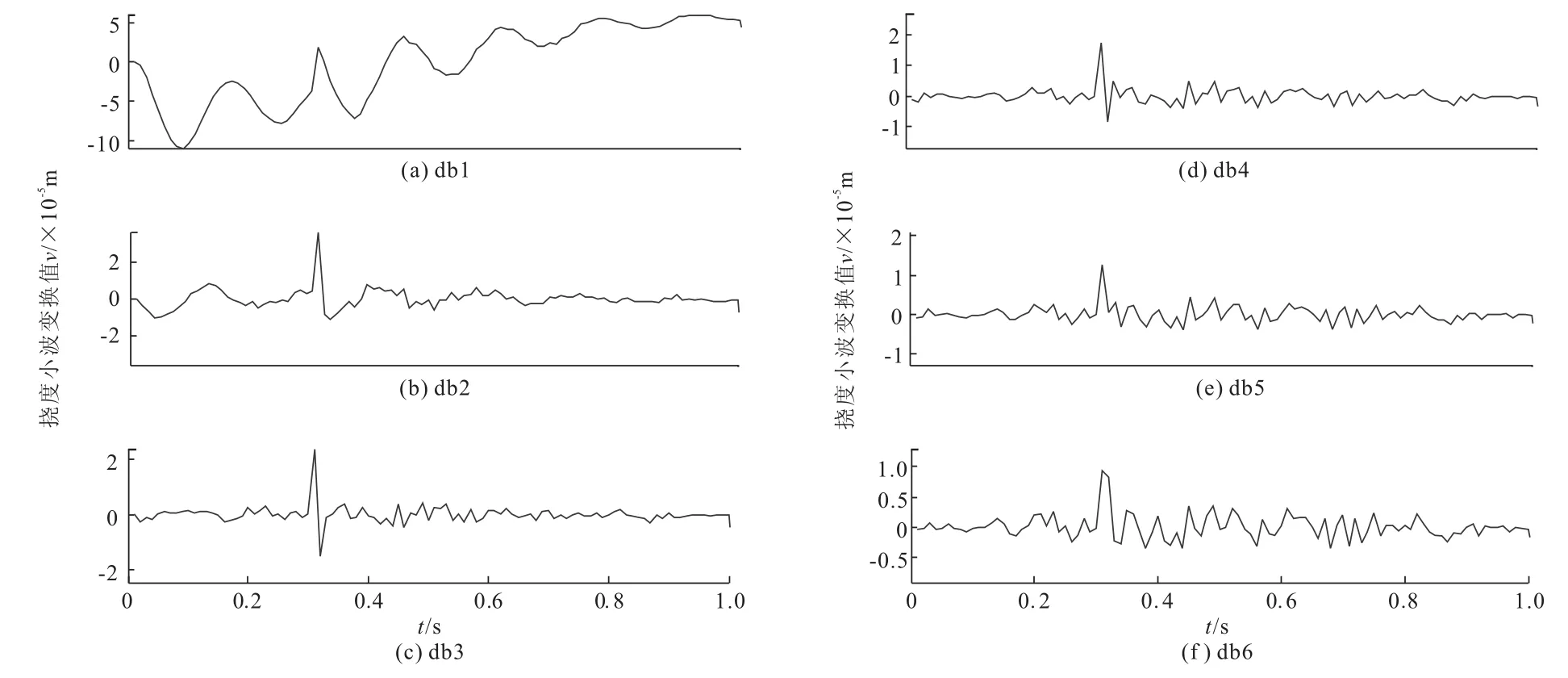
图7 移动荷载作用下裂纹梁跨中测点挠度时程曲线db小波变换

从图8a中可以看出，当荷载噪声标准差为10 N时，所考虑各种深度裂纹均能较好地通过小波变换识别出。但当荷载噪声标准差增大至200 N时（如图8b），随之增大的挠度响应随机性“淹没”了0.2和0.4裂纹相对深度引起的位移响应小波变换峰值，而相对深度0.6的裂纹仍然能被较清晰地检测出。随着荷载噪声标准差进一步增大至1000 N时，如图8c所示，所考虑0.2、0.4及0.6裂纹相对深度的位移响应小波变换峰值全被随机荷载噪声的影响所“淹没”而无法被检测出。以上关于移动随机荷载噪声水平与裂纹相对深度的定性研究结果表明，裂纹深度的增加增大了裂纹处位移响应的突变性，使得其更易被小波变换检测出而不被荷载噪声所“淹没”，但当移动荷载随机噪声相对于裂纹深度较大的情况下，裂纹对位移响应影响仍会被噪声所“淹没”。

2.4 随机荷载作用下梁裂纹的多速度检测法

为克服上节中由于移动随机荷载噪声所引起的裂纹检测困难问题，本节引入一系列随机速度移动随机荷载下挠度响应，构建多速度随机挠度响应曲面，再通过系列小波变换以有效检测裂纹位置。

考虑速度均值为60 km/h、标准差为3 km/h的一系列移动随机荷载，假设每次仅单个移动荷载作用在梁上，保持裂纹梁模型参数与上节一致，裂纹相对深度取0.6，且随机荷载噪声水平与上节中所考虑的最大噪声水平1000 N相同，作不同速度荷载下裂纹梁跨中测点挠度时程曲线，构成的响应曲面如图9所示。由于裂纹对于挠度响应的影响很小，如所预料，从该图中无法直接辨别裂纹处突变。对图9不同速度下随机响应曲线分别进行离散小波变换，构建小波变换曲面，如图10所示。其中，图10a很明显地反映出移动随机荷载噪声对于不同移动速度下小波变换结果的影响，尽管在裂纹位置附近小波变换幅较大，但仍不能较明显揭示裂纹位置。相比之下，图10b将小波变换曲面以平面视图方式显示后，可以较清楚地观察到0.3L位置处存在明显裂纹（紫色圈中所示）。

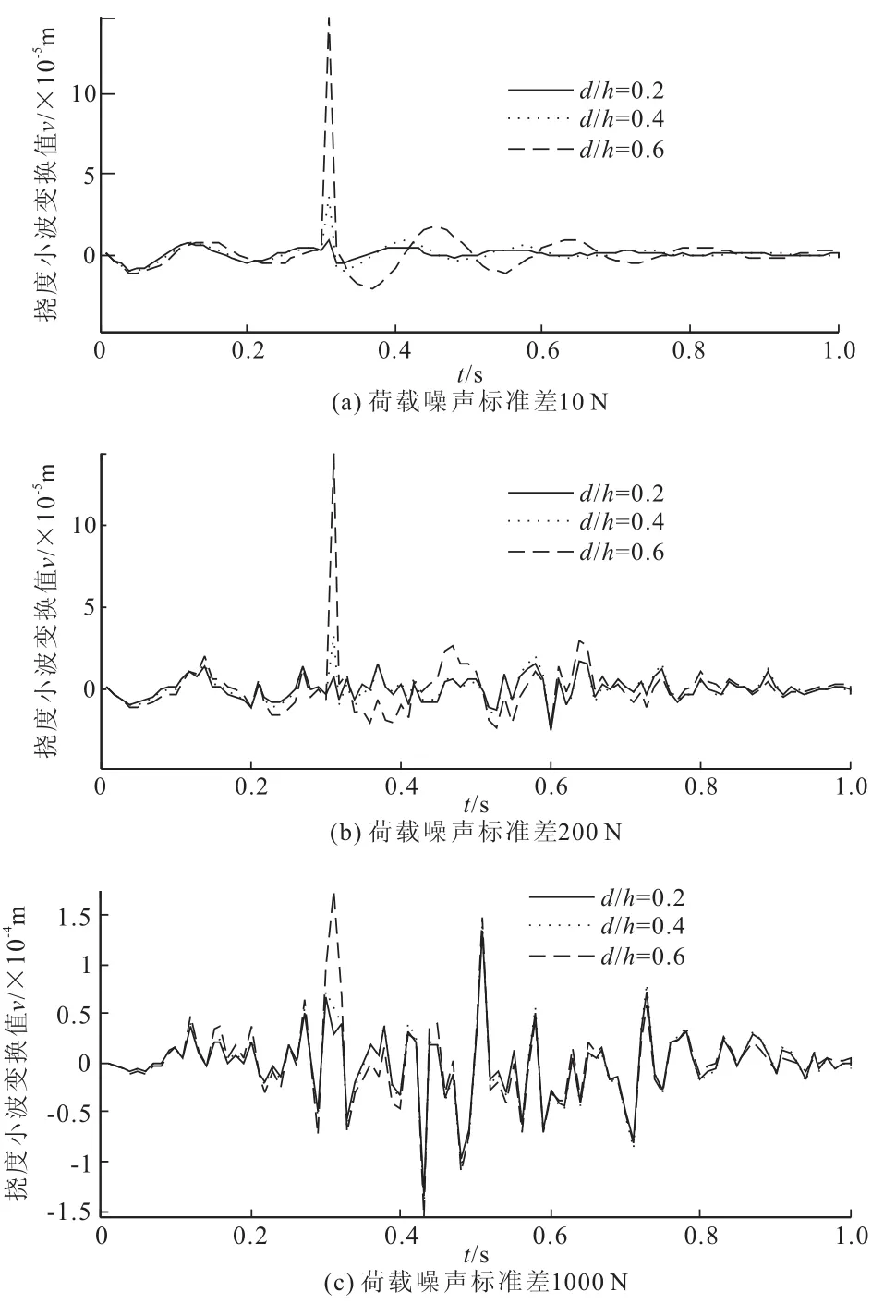
图8 不同标准差不同裂纹深度裂纹梁小波变换对比

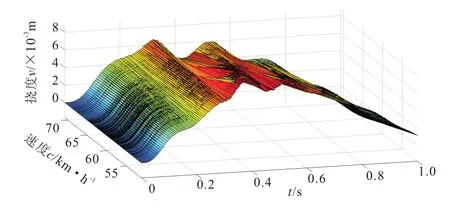
图9 不同速度移动荷载下裂纹梁的跨中挠度时程

此外，考虑到移动荷载的随机性，尝试将不同速度移动随机荷载下裂纹梁跨中挠度响应先取统计平均，再对该均值曲线进行小波变换，试图降低随机噪声影响，计算结果如图11所示。从该图中很明显看出，经过统计平均运算，移动随机噪声对裂纹位置识别的影响大大降低，能非常清晰地定位出裂纹位置。值得指出，尽管不同移动速度下给定测点处的挠度响应曲线形状有所区别，但该多速度响应曲面统计平均方法也能很有效实现裂纹定位，同时也适用于更大随机荷载噪声情况，比前文提出的一种多速度小波变换曲面方法更为有效。

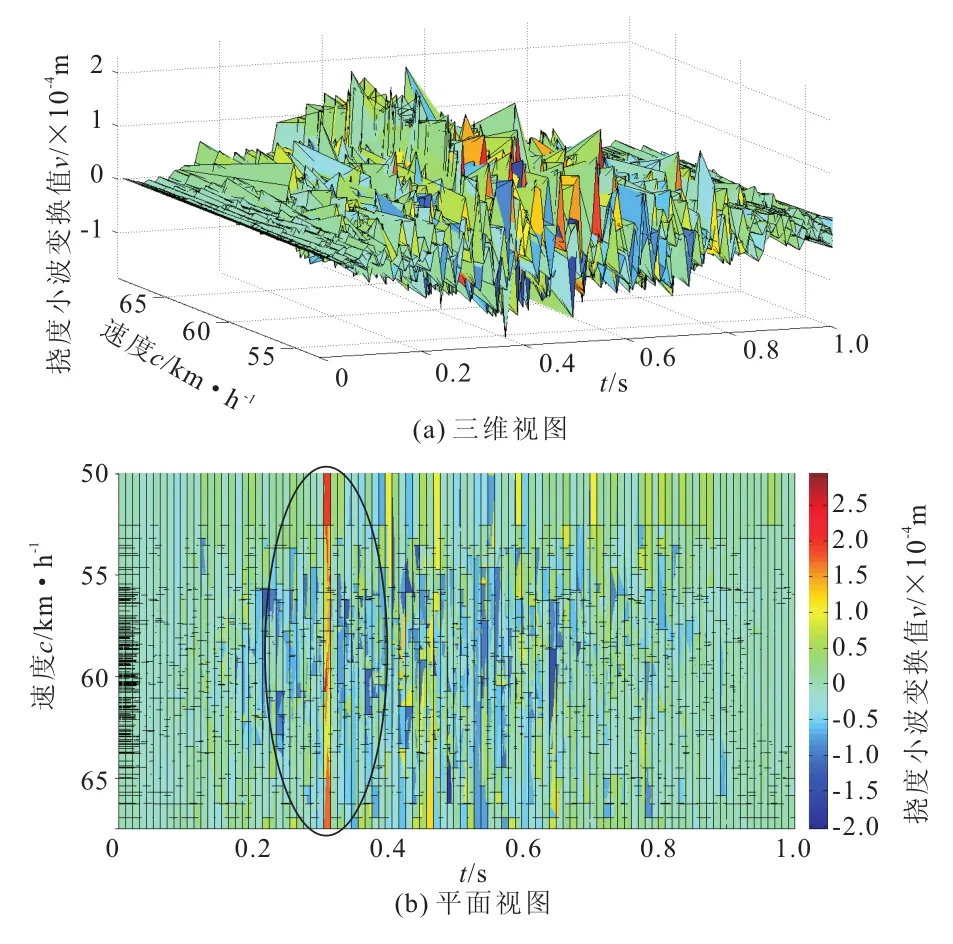
图10 不同速度移动随机荷载下裂纹梁跨中挠度时程的小波变换

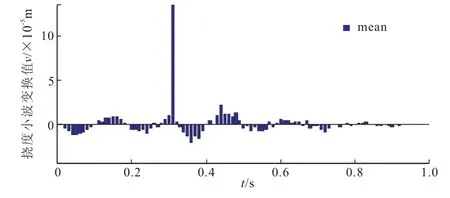
图11 不同速度移动荷载下裂纹梁跨中挠度时程均值小波变换

3 结 论

本文提出了一种匀速移动随机荷载作用下裂纹梁动力响应的理论解，并对裂纹梁随机动力响应与裂纹定位问题进行研究，获得以下主要结论：（1）在含噪声荷载情况下，给定测点位移响应将围绕其均值在一定范围内波动，且波动范围与荷载噪声标准差大小密切相关；（2）通过 Monte Carlo法验证了本文方法求得的移动随机荷载作用下裂纹梁随机位移响应标准差曲线符合正态分布规律，从而证明了本文方法的正确性；（3）在一定荷载噪声水平下，随着裂纹深度的增加，裂纹处位移响应曲线的小波变换突变加强，但当移动荷载随机噪声相对于裂纹深度较大的情况下，裂纹影响仍会被噪声所掩盖；（4）通过引入一系列不同速度移动随机荷载构建裂纹梁位移响应的小波变换曲面，可以较清晰地反映裂纹处突变；（5）通过对不同速度移动随机荷载下裂纹梁挠度响应曲线先取统计平均再进行小波变换，能更有效检测出裂纹位置，更有利于实际应用；（6）本文分析方法可以很方便地推广到多跨、多裂纹情况以及较大随机荷载噪声情况。

［1］Fryba L.Vibration of Solids and Structures Under Moving Loads（3rd edition）［M］.London：Thomas Telford，1999.

［2］Michaltsos G，Sophianopoulos D，Kounadis A N.The effect of a moving mass and other parameters on the dynamic response of a simply supported beam［J］. Journal of Sound and Vibration，1996，191（3）：357-362.

［3］Abu-Hilal M，Zibdeh H S.Vibration analysis of beams with generalboundary conditions traversed by amoving force［J］.Journal of Sound and Vibration，2000，229（2）：377-388.

［4］刘宇飞，辛克贵.移动荷载激励下基于平均曲率模态的简支梁局部损伤识别［J］.工程力学，2013，30（7）：205-211.

［5］Law S S，Lu Z R.Crack identification in beam from dynamic response［J］.Journal of Sound and Vibration，2005，285（4-5）：967-987.

［6］赵 俊，张伟伟，马宏伟.移动载荷作用下简支梁的动态响应及裂纹损伤识别研究［J］.振动与冲击，2011，30（6）：97-103.

［7］吕 峰，林家浩，张亚辉.移动随机荷载作用下桥梁振动分析［J］.振动与冲击，2008，27（12）：73-78.

［8］滕海文，许树峰，李秀芬，等.结构裂缝损伤识别的连续小波分析方法［J］.振动与冲击，2008，27（8）：155-157.

［9］Fryba L.Non-stationary response of a beam to amoving random force［J］.Journal of Sound and Vibration，1976，46（3）：323-338.

［10］Lam H F，Ng C T，Veidt M.Experimental characterization ofmultiple cracks in a cantilever beam utilizing transient vibration data following a probabilistic approach［J］.Journal of Sound and Vibration，2007，305（1-2）：34-49.

Dynam ic Response Analysis and Crack Localization for a Cracked Beam Structure Involving the Randomness of M oving Load

ZHAO Ming-jie，YIN Tao，FU Shao-jun
（School of Civil Engineering，Wuhan University，Wuhan 430072，China）

The problem of random displacement response and crack localization for a simply-supported cracked beam undermoving random load were investigated in this paper.The theoretical solution of displacement response for Euler-Bernoullibeam with a transverse opening crack under a singlemoving random load is developed.The dynamic response of a cracked beam subjected to a moving random force in a constant standard deviation case was firstly studied.Then the theoretical solution of the random displacement response for the cracked beam under themoving random load is verified by using the Monte Carlo simulation method.In addition，to transform the time-domain response measured from limited number of sensors for the beam structure to spatial-domain by noting the uniform property of themoving load velocity，a crack identification method is proposed based on spatial and temporal transformation.In this method，the discrete Daubechies wavelet transform method is employed to analyze the relative relationship between the randomness level of moving random load and the singularity level of displacement response curve at crack location corresponding to certain crack depth.The article ends with the conclusion that crack location can be detected effectively by analyzing the wavelet transform results of the displacement response curves and the average deflection of the cracked beam under repeated moving random loadswith a series of velocities.

moving random load； Monte Carlo simulation method； spatial and temporal transformation；wavelet transform；crack localization

U441+.3

A

2095-0985（2016）04-0102-07

2015-12-04

2016-01-15

赵明杰（1991-），男，浙江东阳人，硕士研究生，研究方向为结构健康监测（Email：guinsoozmj@yeah.net）

尹 涛（1979-），男，湖北汉川人，博士，副教授，研究方向为结构健康监测（Email：tyin@whu.edu.cn）

国家自然科学基金（51208390）