反向响应过程抗负载干扰PID控制回路性能评估
郑克波,栾小丽,刘 飞
(1.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122; 2.江南大学 自动化研究所,江苏 无锡 214122)
反向响应过程抗负载干扰PID控制回路性能评估
郑克波1,2,栾小丽1,2,刘 飞1,2
(1.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122; 2.江南大学 自动化研究所,江苏 无锡 214122)
反向响应过程广泛存在于化工领域中,但针对反向响应过程的性能评估研究较少;针对一类二阶时滞反向响应过程,通过幂级数展开的方法简化了对象模型,然后研究其抗负载干扰PID控制回路性能评估问题;根据DS-d控制原理获取期望闭环传递函数以及PID控制器参数,推导干扰模型为阶跃情况下的PID控制回路累积绝对误差(IAE)性能基准值,并将其推广到斜坡输入以及一般输入情形,为不同干扰类型情况下的反向响应过程建立通用化的IAE性能评价标准;仿真结果验证了所提性能评估算法的正确性以及通用性。
性能评估;反向响应过程;抗负载干扰
0 引言
现代工业过程拥有成千上万的控制器,这些控制器在运行初期性能良好,但是很多因素如设备的老化以及工况环境的变化等都会导致其性能随着时间的推移而逐步减弱[1-2]。为了能够定量地评价当前控制回路的性能状态,性能评估领域的研究在过去的25年间取得了一些列研究成果[3-5]。其中,PID作为当前应用最广泛的控制器,其性能评估研究已经成为一个研究热点[6-7]。如Veronesi和Visioli推导二阶时滞过程在阶跃输入下的PID控制回路IAE性能基准值并给出了性能不佳时的控制器重调算法[8]。
进一步考虑到控制回路中干扰存在的普遍性,针对存在干扰的PID控制回路的性能评估研究对工业生产具有重大意义。在已有的研究成果中, Visioli和Hagglund分别提出了AI(Area Index)和II(Idle Index)性能指标用以检测PI/PID控制回路是否存在振荡和迟缓[9-10];Veronesi和Visioli根据SIMC调整准则,针对带积分环节的过程对象提出了抗输入型负载干扰的性能评估方法[11];YU等针对一阶时滞过程,研究了其抗负载干扰的性能评估问题[12]。
现有的抗负载干扰PID控制回路性能评估文献中,过程对象大多是一阶时滞模型,针对广泛存在于工业过程中的反向响应模型[13-15],其抗负载干扰性能评估的研究非常少,且已有的性能评估大多假设干扰类型为阶跃信号,而在工业实际中,为了避免突变型的信号对机器设备造成负面影响,实际中的干扰变化大多是斜坡类型甚至更一般的类型,这也成为性能评估研究的难点。
本文首次针对二阶时滞反向响应过程抗负载干扰控制回路,推导其在干扰类型为阶跃情况下的抗负载干扰PID控制回路IAE性能基准值,并将其推广到斜坡干扰以及一般类型干扰的情形,针对不同类型的干扰,为反向响应过程建立通用化的抗负载干扰IAE性能评价标准。最后用一个仿真实例来验证本文所提性能评估算法的正确性以及通用性。
1 基于DS-d原理的PID控制

图1 抗干扰控制回路示意图
考虑如图1所示的控制回路,G(s)和C(s)分别代表过程对象和控制器,r(t)、e(t)、u(t)、y(t)、d(t)分别代表设定值、误差、控制信号、输出值和干扰。本文中,控制器具有如下PID形式:
(1)
过程对象模型为一个二阶时滞反向响应过程,表达式如下所示:
(2)
文献[13]中Neng-Sheng Pai针对反向响应过程提出按照幂级数展开的方法,可将1-τas这一项近似为e-τas,即1-τas≈e-τas,则原对象模型可变为:
(3)
其中:θ1=θ+τa。
根据经典控制理论,从干扰到系统输出的闭环传递函数表达式为:
(4)
Chen和Seborg的研究[16]指出DS-d控制原理的基本思想是,期望从d(t)到y(t)的闭环回路传递函数如公式(5)所示,即:
(5)
联立公式(4)和(5),使得分子和分母对应相等,可得PID控制器参数和期望闭环传递函数中的参数kd如下:
(6)
(7)
(8)
(9)
根据DS-d控制原理[17],在给定期望闭环传递函数和过程对象的前提下,根据文献[16]提出的方法,即可求得PID控制器参数。必须强调,本文关心的是控制器性能评估方法,而不是具体的控制器设计,任何合理的控制器设计准则都可以作为性能评估结果不佳时的优化方法。
2 IAE性能基准值和DS-d-IAE性能指标
本节根据DS-d控制原理,首先针对干扰类型为阶跃的情况,推导闭环回路响应的IAE性能基准值。进一步考虑到实际干扰为斜坡类型甚至一般类型信号的情况,推广研究在一般类型干扰情形下闭环回路响应的IAE性能基准值。最后,根据得到的理论基准值,采用DS-d-IAE指标评价控制回路的性能。
2.1 IAE性能基准值
2.1.1 干扰类型为阶跃情况下的IAE性能基准值

基于期望闭环传递函数,可得系统输出:
(10)
对公式(10)进行拉普拉斯反变换,有:
(11)
假定设定值信号r(t)保持在常值零,即r(t)≡0,∀t。若该常值不为零,则需要对数据进行预处理,即将r(t)和y(t)减去该常值。如此,闭环回路的跟踪误差信号为:

(12)
公式(11)中的y(t)就是d(t)阶跃变化下期待的闭环回路输出,与之对应的IAE基准值为:
(13)
注1:由公式(13)可知,在干扰类型为阶跃的情况下,二阶时滞反向响应过程抗负载干扰PID控制回路的IAE性能基准值与反向响应过程的增益K,时延θ,可调参数τc以及不稳定零点τa有关,由此可见,按照幂级数展开的方法将原对象模型进行变换之后,不稳定零点τa对IAE性能基准值的影响仍然存在。
2.1.2 干扰类型为斜坡情况下的IAE性能基准值

图2 斜坡干扰及其分解
考虑如图2(a)所示的干扰类型为斜坡变化情况,

(14)
上式中,k是干扰变化的斜率且先假设k>0,T是干扰从开始变化到最终稳态值所需要的时间。d(t)可以被分解为如图2(b)所示的d1(t)、d2(t)之和,即
(15)
其中:
(16)
对上式进行拉普拉斯变换
(17)
则系统输出为:
(18)
其中:
公式(18)的拉氏逆变换:
(19)
其中:
经过判断,可知y(t)≥0,∀t≥0
则闭环回路的误差信号为

(20)
且e(t)≤0,∀t≥0。
可得对应的IAE性能基准值为:
(21)
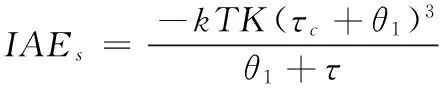
(22)
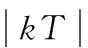
2.1.3 一般类型干扰情况下的IAE性能基准值

图3 一般类型干扰及其分解
假设干扰d(t)按照如图3所示的路径,从一个稳态值过渡到另一个稳态值,则它可由一系列的斜坡信号叠加而成,即
(23)
其中:
其中:ki表示di(t)的斜率;d(t0)与d(tN)分别是d(t)的初始稳态值和最终稳态值,即当t≤t0时,d(t)=d(t0),当t≥tN时,d(t)=d(tN)。根据叠加原理可得抗负载干扰控制回路IAE性能基准值为:
(24)
其中:IAE[di(t)]代表第i个斜坡信号di(t)的性能基准值。欲使公式(24)第二行等式成立,必须满足以下条件之一:1)所有的di(t)的斜率具有相同的正负号,即设定值d(t)单调变化;2)若某两个相邻时刻斜率的正负号不同,则前一时刻的输入必须保持足够长的时间直至闭环回路的响应进入稳态。假设上述条件至少满足一个,忽略d(t)的分解误差,则IAE性能基准值为:
(25)
注3:由公式(25)可以看出,阶跃干扰以及斜坡干扰情况下所得的IAE性能基准值,都是一般干扰情形下的特殊情况,因此利用本文方法所得的IAE性能基准值并不依赖于干扰类型,针对不同类型的干扰,具备一定的通用性。
2.2 DS-d-IAE性能评估方法
2.2.1 DS-d-IAE性能评估指标
针对二阶时滞反向响应过程的PID控制回路,根据获得的IAE性能基准值,可采用文献[12]中提出的DS-d-IAE指标来评价控制回路的性能。该指标是适用于阶跃、斜坡和一般类型干扰下的无量纲性能评估指标,为实际IAE值和IAE基准值中较小值与较大值的比例:
(26)


表1 3种干扰情况在不同N值情况下的PID参数,IAE基准值和IAE实际值
2.2.2 性能评估步骤
针对单回路反向响应过程PID控制系统,在得到它的相应的性能基准值之后,其完整的PID控制回路性能评估步骤如下所示。
Step1:根据给定的过程对象传递函数和期望闭环传递函数,按照可调参数τc的不同取值,对照公式(25)求取对应情况下抗负载干扰回路IAE性能基准值;

Step3:按照公式(26)计算DS-d-IAE性能评估指标,判断系统性能是否良好(工业中常以0.6为分界点,即η≥60%视为控制系统运行良好);
Step4:若系统运行良好,则不需要进行其他操作;若系统运行效果较差(η<60%),则返回Step2;
3 仿真实例

阶跃类型干扰:d(t)=1(t),
斜坡类型干扰:

一般类型干扰:

分别按照公式(13)、公式(21)和公式(25),求取阶跃、斜坡以及一般类型干扰情况下PID控制闭环回路抗干扰响应的IAE理论基准值IAEs,其中期望闭环传递函数的时间常数τc按照θ的N整数倍变化,即λ=Nθ。另外,取采样时间 Ts=0.1秒,获得闭环回路实际IAE值IAEa如表1所示。
注4:N的选取要保证在当前可调参数的情况下,系统是稳定的。在系统稳定的前提下讨论性能评估才有意义。
从表1中可以看出,针对反向响应过程对象模型,其抗负载干扰PID控制回路IAE性能基准值与仿真所得的实际值非常接近,能够有效地验证所提算法的正确性
4 结论
由于不稳定零点的存在,导致之前学者研究的性能基准值不适用于反向响应过程。本文针对二阶时滞反向响应过程,通过幂级数展开的方法将其简化为二阶加时滞模型,然后研究了其抗负载干扰PID控制回路性能评估问题。考虑到工业实际的干扰类型,进一步将其推广到斜坡干扰以及更一般类型干扰情形,为反向响应过程抗负载干扰建立了通用化的IAE性能评价标准。仿真实例验证了所得IAE基准值的正确性。
[1] 薛美盛, Fei Q,等. 控制回路性能评估综述[J]. 控制工程, 2009, 16(5): 507-512.
[2] Jelali M. An overview of control performance assessment technology and industrial applications[J]. Control Engineering Practice, 2006, 14(5): 441-466.
[3] Harris T J. Assessment of control loop performance[J]. The Canadian Journal of Chemical Engineering, 1989, 67(5): 856-861.
[4] Pillay N, Govender P. A data driven approach to performance assessment of PID controllers for setpoint tracking[J]. Procedia Engineering, 2014, 69(1): 1130-1137.
[5] Sendjaja A Y, Kariwala V. Achievable PID performance using sums of squares programming[J]. Journal of Process Control, 2009, 19(6): 1061-1065.
[6] Garpinger O, Hagglund T, Astrom K J. Performance and robustness trade-offs in PID control[J]. Journal of Process Control, 2014, 24(5): 568-577.
[7] Yu Z, Wang J, Huang B, et al. Performance assessment of PID control loops subject to setpoint changes[J]. Journal of Process Control, 2011, 21(8):1164-1171.
[8] Veronesi M, Visioli A. Performance assessment and retuning of PID controllers[J]. Industrial & Engineering Chemistry Research, 2009, 48(5): 2616-2623.
[9] Visioli A. Method for proportional-integral controller tuning assessment[J]. Industrial & Engineering Chemistry Research, 2006, 45(8): 2741-2747.
[10] Hägglund T. Automatic detection of sluggish control loops[J]. Control Engineering Practice, 1999, 7(99): 1505-1511.
[11] Veronesi M, Visioli A. Performance assessment and retuning of PID controllers for load disturbance rejection[J]. Advances in Pid Control, 2012, 2(1):530-535.
[12] Yu Z, Wang J. Assessment of proportional-integral control loop performance for input load disturbance rejection[J]. Industrial & Engineering Chemistry Research, 2012, 51(36):11744-11752.
[13] Pai N S, Chang S C, Huang C T. Tuning PI/PID controllers for integrating processes with deadtime and inverse response by simple calculations[J]. Journal of Process Control, 2010, 20(6): 726-733.
[14] Jeng J C, Lin S W. Robust proportional-integral -derivative controller design for stable/integrating processes with inverse response and time delay[J]. Industrial & Engineering Chemistry Research, 2012, 51(6): 2652-2665.
[15] Huang W, Chiu M S. Direct design of PID controllers for stable processes with inverse response[A]. SICE Annual Conference (SICE) [C], Sapporo, 2014: 165-170.
[16] Chen D, Seborg D E. PI/PID controller design based on direct synthesis and disturbance rejection[J]. Industrial & engineering chemistry research, 2002, 41(19): 4807-4822.
[17] Rao A S, Rao V S R, Chidambaram M. Direct synthesis-based controller design for integrating processes with time delay[J]. Journal of the Franklin Institute, 2009, 346(1):38-56.
Assessment of Inverse Response Process PID Control Loops Performance for Load Disturbance Rejection
Zheng Kebo1,2, Luan Xiaoli1,2, Liu Fei1,2
(1.Ministerial Key Lab. of Advanced Process Control for Light Industry,Jiangnan University,Wuxi 214122, China;2.Institute of Automation, Jiangnan University, Wuxi 214122, China)
Although inverse response process exists widely in the field of chemical industry, studies for the performance assessment of it are not very common. The inverse response process with second order plus time-delay model is simplified by a truncated power-series expansion, then assessment of PID control loops performance for load disturbance rejection is discussed. The integrated absolute error(IAE) performance benchmark is established from closed-loop responses with step type of load disturbance changes, while the desired closed loop transfer function and the PID controller parameters is acquired through the DS-d control principle. In addition, the general IAE performance benchmark for different types of load disturbance is put forward for inverse response process subject to ramp and other general types of load disturbance changes. Numerical example is employed to demonstrate the effectiveness and universality of the proposed performance assessment algorithm.
performance assessment;inverse response process;load disturbance rejection
2015-08-27;
2015-09-25。
国家自然科学基金资助项目(61104121);江南大学自主科研计划重点项目(JUSRP51407B)。
郑克波(1991-),男,浙江乐清人,硕士研究生,主要从事PID控制回路性能评估方向的研究。
栾小丽(1979-),女,江苏人,副教授,硕士研究生导师,主要从事复杂系统先进控制与优化方向的研究。
1671-4598(2016)06-0289-05
10.16526/j.cnki.11-4762/tp.2016.06.079
TP273
A
刘 飞(1965-),男,安徽人,教授,博士生导师,主要从事先进控制理论与应用、过程监控等方向的研究。

