基于ANSYS/Fluent的主喷嘴外流场分析

刘　育，王益轩，姚　超，刘婷婷，王　瑶

(西安工程大学 机电工程学院，西安　710048)



基于ANSYS/Fluent的主喷嘴外流场分析

刘育，王益轩，姚超，刘婷婷，王瑶

(西安工程大学 机电工程学院，西安710048)

为获得喷气织机稳定的引纬气流，提高喷气织造的效果，根据主喷嘴的结构对喷气织机用主喷嘴的结构和喷气引纬系统进行优化，通过建立三维模型并用ANSYS/Fluent进行仿真，对不同主喷嘴出口直径和速度下的自由紊动射流流场进行了详尽的图形分析和数值模拟计算。指出：主喷嘴采用直径为4 mm～6 mm的小喷口，可获得更加稳定的引纬气流；主喷嘴外流场的射流喷口直径与异形筘的安装位置和气流槽高度相关；数值模拟与理论解吻合较好，可为后续研究提供指导。

喷气织机；引纬；主喷嘴；辅喷嘴；喷口；直径；气流；射流；紊流；ANSYS/Fluent

0　引言

引纬机构是喷气织机的关键机构，其性能很大程度决定喷气织造的效果。喷气引纬，是利用高速流动的空气对纱线表面产生的摩擦力将纱线引过梭口。引纬时，主喷嘴将高速压缩空气喷向异形筘气流槽，筘座上以适当的间距安装多个辅喷嘴，相继向气流槽内喷射补充气流，主喷嘴气流和辅喷嘴气流交汇形成的高速气流使纬纱顺利引过梭口。辅喷嘴数量和安装间距取决于筘幅和纬纱特性。

笔者研究主喷嘴产生的流场，也就是由导纱管喷射的外流场特性，对主喷嘴外流场的展开是在未考虑异形筘影响的前提下进行的；而异形筘限流下有限空间的紊动射流，是个非常复杂的紊动流场问题，目前在理论上还不太成熟，大多根据实验结果整理成工程实用的曲线供使用参考，在此不作论述。

1　主喷嘴结构

如图1所示，主喷嘴由喷嘴芯A、喷嘴体B、导纱管C组成。高速气流从入口进入主喷嘴，经过环形气室及整流槽后，高速气流由湍流变为沿直线流动的层流气流；特别设计的整流器与喷嘴体共同构成沿周向均匀分布的整流条槽，通常有4条～24条之多[1]；层流气流经过亚音速加速区、锥形套后，气流速度再次得到提高；在通过喉部、喉部出口后，速度达到最大至接近或超过音速，并依靠纬纱在引射区内形成的负压区，外界大气携带纬纱进入纬纱加速区；高速气流携带纬纱在导纱管内高速运动，使纬纱达到引纬要求的速度。

2　主喷嘴外流场有限元模型建立

对喷气织机引纬系统主喷嘴的外流场，建立贴近实际情况的三维模型，即分别建立直径为4 mm、5 mm、6 mm、7 mm、8 mm模型，同时在150 m/s、200 m/s、250 m/s、300 m/s、350 m/s的射流速度下，使用ANSYS/Fluent进行仿真分析，具体如下。

a)几何模型，只研究主喷嘴的外流场即从导纱管出来以后的自由射流区,使用Pro/E建立三维模型，保存为IGES文件格式，确保模型数据能够传入ANSYS/Fluent软件。

b)网格划分，使用ICEM CFD，采用结构化的六面体网格如图2所示，单元数量为89万。网格质量评价系数如下：0.85～1.00(79.417%)、0.70～0.85(18.684%)、0.65～0.70(1.899%)的网格质量在0.65以上，该三维模型网格质量能够满足求解精度和收敛要求。文中其他直径入口的三维模型网格，类型与上述一致、网格质量基本相同。

c)边界条件，入口类型为速度入口，取5种不同速度；出口类型为压力出口，大小为标准大气压，其他为壁面。

d)求解器与计算模型，采用基于压力的SIMPLE求解器,标准k-ε二方程模型。

e)材料设置，主喷嘴外流场为空气。

3　主喷嘴外流场模拟计算结果

在紊流自由射流条件下，不同喷射速度对不同直径的主喷嘴外流场进行模拟，求解使用后处理软件提取数据，计算结果如下。

3.1射流轴向速度及紊流强度

直径分别为 4 mm、5 mm、6 mm、7 mm、8 mm的喷口，在射流速度为150 m/s、200 m/s、250 m/s、300 m/s、350 m/s下的射流轴向速度分布和紊流强度分布如图3～图12所示。

由图3～图12可知，气流从喷口喷出，在紊流强度达到最大值之前，气流沿轴向速度衰减变化不大，适合于引纬。计算出主喷嘴不同出口直径和速度下，达到预定引纬速度的最佳轴向距离(从喷口到紊流强度达到最大值之前位置的轴向距离)，见表1。超出此最佳轴向距离时，气流将很快衰减，不能达到预定的引纬速度，则必须沿着主喷嘴射流轴向加装辅喷嘴[2]。

由图3～图12可知，不同直径喷口中心轴向速度和紊流强度的变化，表明在喷口附近出口的速度有所升高，接着速度有一小段下降，之后持续下降。

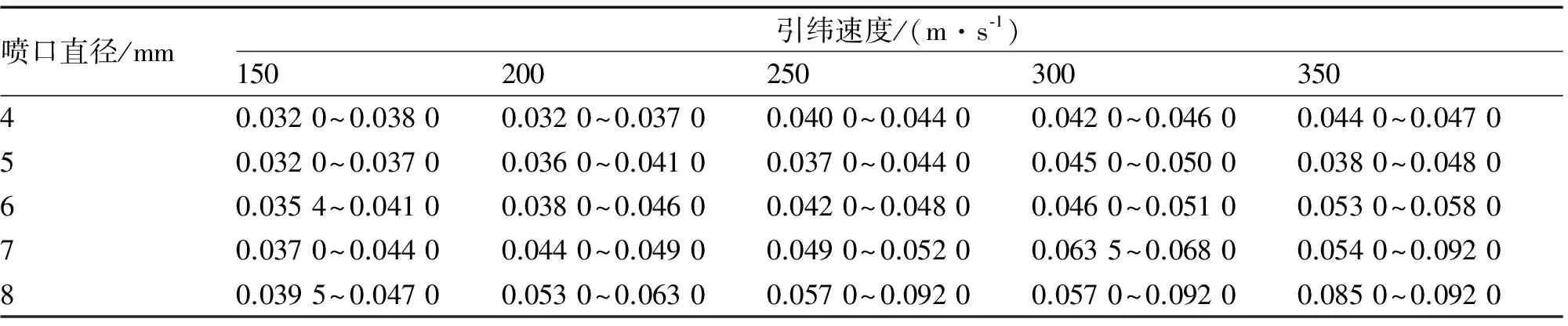
表1　预定引纬速度下主喷嘴射流的最佳距离范围　单位：m

利用气体动力学理论可以较好地解释——出口处的气体由于膨胀而速度升高、产生膨胀波；膨胀波在自由边界中会反射出压缩波,压缩波作用于膨胀波，会使速度下降[3]。与此对应的紊流强度，在喷口附近的射流核心区变化很小，之后持续上升达到峰值后持续下降。对于紊流强度的变化，根据射流理论，射流从喷嘴出口处射出以后形成核心区，其动量、速度最大，紊流强度很小[4]；靠近射流核心区的边界层不断与周围介质进行质量、动量交换，带动了周围原来静止状态的气体，因而自身动量减小、速度逐渐缓慢、紊流强度增大，达到最大值；当边界层与周围介质质量、动量交换减少时，紊流强度减小；最后，射流能量全部消失而无质量、动量交换时，紊流强度趋于稳定值。

由表 1可知，直径为4 mm、5 mm、6 mm喷口轴向位置在0.03 m～0.06 m，但直径为7 mm、8 mm的轴向位置范围变化较大，为0.037 m～0.092 m。对于直径为7 mm、8 mm的喷口，其射流核心区较大，质量、动量也较大，边界层与周围介质质量、动量交换时的能量损失较小，中心轴向速度下降缓慢；但速度波动较大，同时气耗也增加。大直径射流出口，对不同速度的射流集束性较差，不利于纬纱的稳定飞行；且其出口紊流强度峰值大于小口径射流，与小口径出口相比，峰值位置远离喷口位置。

3.2射流核心区的长度

直径为4 mm、5 mm、6 mm、7 mm、8 mm喷口射流核心区的长度(云图下方的深色区)分别如图13～图17所示。

由图13～图17可知，射流核心区的长度与喷口直径有关，随喷口直径增加而增大，这与自由射流理论一致。不同出口直径的核心区位置不同，在满足喷气织机对引纬速度要求时，射流轴向位置会有所不同，也就是说射流在异形筘气流槽内的轴向位置不同。

3.3射流截面处的射流锥直径

分别取距离φ4 mm喷口射流轴向0.002 m、0.007 m、0.012 m、0.017 m、0.022 m的截面，其射流锥直径如图18～图22所示。其他直径的喷口也完全遵循自由射流理论，这里就不再叙述。

由图18～图22可知，射流锥直径与喷口直径和距离喷口的位置有关，随喷口直径和位置增加而增大，这与自由射流理论一致。当喷口直径一定时，距离喷口不同位置的射流锥大小不同。对不同的异形筘气流槽高度，在距离同一喷口位置，获得不同的射流流量；对相同的异形筘气流槽高度，在距离喷口的不同位置，同样也获得不同的射流流量。其他喷口直径的射流锥，其变化规律与本文论述一致，在此不再赘述。

4　数值模拟计与理论解的比较

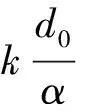
5　结论

5.1主喷嘴外流场采用直径为4 mm～6 mm的小喷口射流直径，可获得更加稳定的引纬气流，更适合引纬。在达到对喷气织机要求为80 m/s～120 m/s引纬速度时，小直径喷口射流都落在距离喷口轴线位置为0.03 m～0.06 m内，这可以对辅喷嘴的安装位置提供一定的参考。

5.2主喷嘴外流场的射流喷口直径与异形筘的安装位置和气流槽高度相关，合适的位置和槽高，能更好地利用出口的速度引纬，使射流流量尽量多的射入异形筘气流槽内。

5.3数值模拟与理论解吻合较好，说明数值模拟的合理性，可为后续研究提供指导。

[1] 路翔飞.喷气织机主喷嘴的局部结构优化及喷射性能分析[D].苏州：苏州大学，2010.

[2] 刘丁丁.喷气织机引纬流场的数值模拟与实验研究及主喷嘴结构优化[D].苏州：苏州大学，2012.

[3] 董志勇.射流力学[M].北京：科学出版社，2005.

[4] 汪旺.喷气织机辅助喷嘴及合成气流场的数值仿真[D].杭州：浙江理工大学，2012.

[5] 张国平.喷气织机引纬原理与工艺[M].北京：中国纺织出版社，2005.

[6] 陈文义,张伟.流体力学[M].天津：天津大学出版社，2004.

Analysis of the External Flow Field of the Main Nozzle Based on ANSYS/Fluent

LIU Yu,WANG Yixuan,YAO Chao,LIU Tingting,WANG Yao

(College of Mechanical and Electrical Engineering Xi’an Polytechnic University,Xi’an 710048,China)

To obtain a stable weft-in flow on the air-jet loom,and to improve the effect of the air-jet weaving,according to the structure of main nozzle of air-jet loom,the jet weft-in system is optimized.Through the establishment of 3D model and ANSYS/Fluent simulation of different primary nozzle exit diameter and velocity of free turbulent dynamic jet flow field were discussed in details with graphics analysis and numerical simulation.It is pointed out that the main nozzle with a diameter of 4 mm～6 mm can get more stability of weft-in flow.The main nozzle diameter of the outside flow and the installation position of the profiled reed and the airflow grooves are highly correlated.The numerical simulation and theoretical solution are in good agreement,providing guidance for the follow-up study.

air-jet loom;weft-in;main nozzle;auxiliary nozzle;nozzle;diameter;flow;jet;turbulent flow;ANSYS/Fluent

2016-03-27

陕西省科技攻关项目(2015GY137)

刘育(1984—)，男，陕西乾县人，硕士，主要从事机械CAD/CAE/CAM及虚拟样机的研究。

TS103.33

A

1001-9634(2016)04-0005-06