多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件

张钱江, 戴世坤, 陈龙伟, 强建科, 李昆, 赵东东

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083 2 中南大学地球科学与信息物理学院, 长沙 410083 3 桂林理工大学地球科学学院, 桂林 541004



多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件

张钱江1,2,3, 戴世坤1,2*, 陈龙伟3, 强建科1,2, 李昆1,2, 赵东东1,2

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083 2 中南大学地球科学与信息物理学院, 长沙 410083 3 桂林理工大学地球科学学院, 桂林 541004

在多源直流电阻率法有限元三维数值模拟中,传统混合边界条件由于刚度矩阵与源点位置相关,无法实现线性方程组的快速回代求解,目前常用齐次边界条件或无限元边界进行替代,虽然实现了快速回代求解,但同时也降低了数值模拟的精度.为了实现快速回代求解,并确保数值模拟的计算精度,本文提出了一种近似边界条件方法.其核心思想是将与场源位置相关的边界系数矩阵从刚度矩阵中分离出来,使得分离后的刚度矩阵与场源位置无关.并将边界系数矩阵与边界处一次电场向量的乘积移到线性方程组右端源项中,当场源位置发生改变时,只需要重新计算右端源项就可以实现快速回代求解.理论模型数值计算表明,在水平地形条件下,本文边界条件数值精度优于混合边界条件;在起伏地形条件下,与齐次边界条件相比,本文边界条件数值结果与混合边界条件吻合度更高.关键词 直流电阻率法; 有限单元法; 边界条件; 数值模拟

1 引言

直流电阻率法作为地球物理勘探中最古老的勘探方法之一,早已广泛应用于矿产资源勘探,水文地质调查,工程勘察等领域(徐世浙, 1994; White et al., 2001; 李金铭, 2005; Rucker et al., 2010; Loke et al., 2013).随着勘探难度的加大和方法应用的深入,以多源激发和大面积观测为代表的三维精细勘探成为研究热点(Loke and Barker, 1996; Nyquist and Roth, 2005; 吴小平等, 2015),从而对多源条件下数值模拟的计算精度和计算效率提出了更高的要求.截断边界问题和线性方程组的求解问题是影响多源条件直流电阻率法有限单元法三维数值模拟计算精度和计算效率的两个重要因素.

针对截断边界问题,目前最常用的做法是采用混合边界条件(Dey and Morrison, 1979),该算法假设前提为: (1) 点电源位于水平地形上; (2) 模型区域Ω内部的电性不均匀性对无穷边界Γ∞上的电位分布不产生影响,其电位是点电源电位.因此,在均匀介质背景模型中采用混合边界条件可以获得较高的数值精度,但是在层状介质背景模型中由于假设条件并不严格,边界区域依然存在截断边界的影响.此外,由于刚度矩阵与场源位置相关,当场源位置发生改变时需要重新计算刚度矩阵,从而导致多源条件数值模拟的计算效率低下.为了解决这个问题,Zhao和Yedlin(1996)采用求取异常电位的方法(Lowry et al., 1989),对二次场电位施加Dirichlet边界条件:ψ=0(ψ为二次场电位),由于ψ按照c/r2规律衰减,该方法具有非常高的数值精度.但是,异常电位法需要非常精确的一次场电位,因而很难应用到起伏地形模型计算中.阮百尧等(2001)认为混合边界条件中边界距离源点位置r较远,可以看成常数,从而使得刚度矩阵在源点移动过程中保持不变.强建科和罗延钟(2007)在上述观点基础上采用Choleshy对刚度矩阵进行分解,当场源位置发生改变时,通过回代求解提升了正演数值模拟的计算效率.黄俊革等(2003)采用齐次边界条件(Neumann boundary),认为当r→∞时,混合边界条件中cos(r,n)U/r→0,因此,只需要选取适当的边界距离,截断边界的影响就可以忽略.Blome等(2009)采用无限元法处理边界问题,该方法与Dirichlet和混合边界条件相比缩小了计算范围,并减少了计算量.汤井田和公劲喆(2010)在有限元-无限元法中,提出了一种全新的最优的无限元形函数,然后将其与非结构化四面体有限元相结合,使得电位在无限域内连续并在无限远处衰减为零,在相同计算范围下该方法计算精度优于齐次边界条件,并在近似测区大小的计算范围内与混合边界条件计算精度相当.

在线性方程组求解中,多源向量求解问题的快速计算一直是研究的难点和热点.线性方程组的求解主要包括两大类:迭代求解法(Saad, 1996; Saad and Van der Vorst, 2000)和直接求解法(Davis, 2006).由于迭代求解法具有消耗计算资源低和在许多情况下收敛较快的优点,在直流电阻率法三维数值模拟中占有主导地位(Dey and Morrison, 1979; Ajiz and Jennings, 1984； Spitzer, 1995; Zhang et al.,1995; Zhou and Greenhalgh, 2001; Li and Spitzer, 2002; Wu et al., 2003; 吴小平和汪彤彤, 2003).随着计算机计算能力的飞速发展,稀疏矩阵的直接求解法开始出现(Liu, 1992; Schenk et al., 2001).该方法虽然需要耗费大量的时间对稀疏矩阵进行分解,并占用巨额的内存资源,但是只需要分解一次就能实现多源向量的快速回代求解.因此,在多源向量求解问题中和需要大量正演计算的反演问题中具有很大的应用潜力,并已经被应用到电磁法三维勘探中(Oldenburg et al., 2008; Arunwan and Siripunvaraporn., 2010; Yang and Oldenburg, 2012; Schwarzbach and Haber, 2013; Grayver et al., 2013; 韩波等, 2015; 杨军等, 2015). Blome等(2009)将基于“Pardiso”的直接求解法应用到直流电阻率法有限元三维数值模拟中,并与预条件共轭梯度法(PCG)进行了对比研究,研究结果表明,在多源向量求解问题中直接解法优势更大.

针对多源条件直流电阻率法有限元三维数值模拟中常用边界条件存在的问题,本文提出了一种全新的近似边界条件方法: (1) 从电位与电场的相互关系出发给出半无限边界上电位满足的边界条件; (2) 将边界系数矩阵从刚度矩阵中分离出来,并将其与边界处一次电场向量的乘积移到线性方程组右端源项中; (3) 采用直接解法求解器对分离后的刚度矩阵进行三角矩阵分解; (4) 当场源位置发生改变时,通过重新计算右端源项实现快速回代求解.文中详细论述了近似边界条件的计算方法,并给出了均匀背景模型和层状介质模型中边界处一次电场的计算表达式,最后通过理论模型验证了本文算法的有效性.

2 有限单元法基本原理

双点电源置于三维无限半空间Ω的表面Γs时,电位满足微分方程(Xu, 1994)

(1)

其中σ为介质电导率,U为电位,I为点源供电电流,δ为狄拉克函数,A和B分别为点源供电点所在位置,A点供正电流,B点供负电流(后文同).

在地面Γs上，电位满足的边界条件为

(2)

在半无限边界Γ∞上,目前常用的边界条件有

(3)

其中n为外法向方向,rA和rB分别为点电源A和B距离边界的距离,f(x,y,z)为已知函数,在数值模拟中通常取f(x,y,z)=0.

三维直流电阻率法双点电源边值问题由式(1),(2)和(3)组成.基于变分原理,可以得到与边值问题等价的变分问题(以混合边界条件为例)

(4)

采用四面体单元进行空间离散,离散方案为:首先将模型进行六面体单元剖分,然后在六面体中进行四面体单元的剖分(熊彬等, 2003).六面体单元剖分成六个四面体单元的方法参考文献(Zhou and Greenhalgh, 2001),该剖分方法具有很好的数值对称性和数值精度.在四面体单元中采用双线性插值函数:

(5)

其中Ni为插值形函数,与四面体自然坐标Li相同(徐世浙, 1994),Ui和σi分别为节点上的电位值和电导率值.

对变分问题(4)各项单元分析后所得的结果相加,再扩展成全体节点组成的矩阵或列阵.由全部单元相加,得

(6)

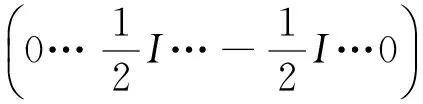
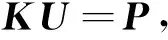
(7)

其中K=K1+K2,为对称、正定的大型稀疏矩阵.

对于线性方程组(7),我们设计了电阻率为100 Ωm的均匀半空间模型,对常用不完全Cholesky分解共轭梯度法(ICCG)(Wu et al., 2003)和Pardiso求解器的求解性能进行了测试,测试结果见表1.模型测试中,模型网格做均匀剖分,共轭梯度法迭代终止条件为均方根误差ε≤10-5,测试计算机配置为CPU-InterXeon(R)E5-2687W,主频3.10GHz,内存256.00GB.

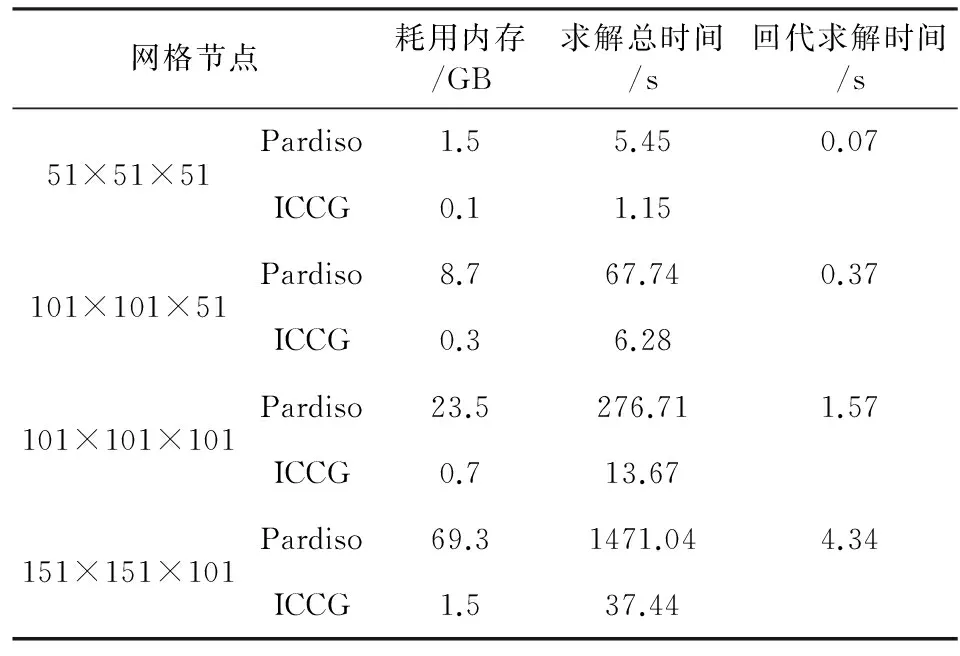
表1 不同维数线性方程组求解参数Table 1 Parameters of linear equations with different dimensions

从表1我们可以看出,单个场源的正演计算中,ICCG具有很大的优势,且随着维数的增加优势越大.但当场源较多时,Pardiso只需要耗费非常短的时间就能完成线性方程组回代求解,考虑到多源条件下直流电阻率法三维反演的计算效率需求,我们对两种解法在反演计算中求解线性方程组总耗时进行粗略估算,以共轭梯度法反演为例(Ellis and Oldenberg, 1994; Zhang et al., 1995;吴小平和徐果明, 2000):假设ICCG和Pardiso求解一次线性方程组总时间分别为tICCG和tPardiso, Pardiso求解中回代求解时间为tbackward,激发场源个数Ns为50个,反演迭代次数Niter为10次,每次迭代中共轭梯度内循环Ncg为8次.则共轭梯度反演过程中两种求解方法求解方程组总耗时计算表达式分别为

(8)

×Niter.

(9)

根据计算表达式(8)和(9)我们可以估算出两种解法在不同维数反演计算中求解线性方程组总耗时以及求解效率比,计算结果见表2.从估算结果中我们可以看出,在多源条件直流电阻率法三维共轭梯度反演计算中,当计算机硬件满足计算要求时,采用直接解法具有更高的计算效率.此外,在实际计算过程中当条件数较差时将大大增加迭代求解法的计算时间,而直接求解法不受这一因素的影响.

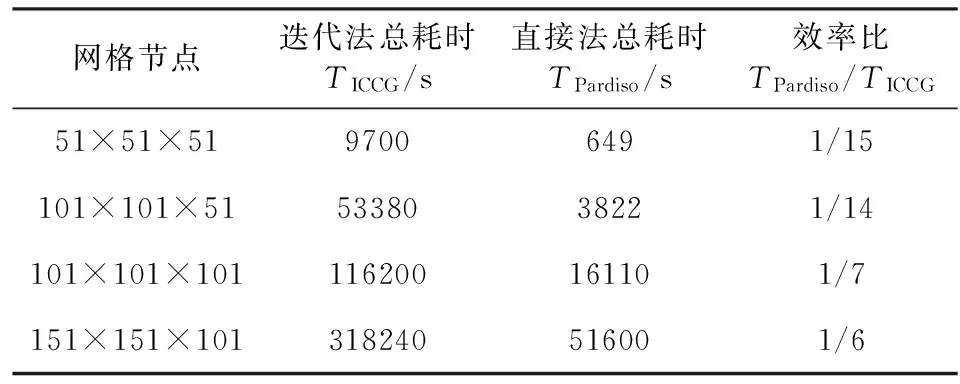
表2 两种解法在共轭梯度反演中 求解方程组总耗时估算Table 2 Total estimated time cost in resolving linear equations with conjugate gradient inversion in the two methods

3 边界条件算法

由式(7)可知,采用有限单元法得到的线性方程组可以表示为

K1U+K2U=P.

(10)

常用边界条件中(如式(3)所示):Dirichlet边界条件通常将Γ∞取得足够远,近似认为U|Γ∞=0,由于边界区域取得足够大,需要增加大量的计算节点,从而降低了计算效率.该方法也可以近似认为U|Γ∞为截断边界上一次场电位值,这样Γ∞就不必取得很大,从而降低了计算工作量.徐世浙(1994)在位场延拓有限单元法数值模拟中详细论述了这种方法的加载方法.

K1U=P.

(11)

混合边界条件相比其他两种边界条件,具有更高的数值计算精度,但由于K2与源点位置相关,当源点位置发生变化时需要重新计算边界项系数矩阵K2,因此在多源条件下无法实现线性方程组的快速回代求解.针对这个问题,阮百尧等(2001)将K2中与源点位置相关的r看成常数,使得边界项系数矩阵K2在源点移动过程中保持不变.这种假设在测线较长,源点位置移动较大时存在较大的数值误差.

综合上述三种边界条件方法,针对多源条件直流电阻率法三维数值模拟的计算效率和计算精度问题,本文提出了一种近似边界条件方法:该方法取具有解析解或数值滤波解的背景模型计算出边界一次电场E0,并作为边界上的值,然后将其与边界单元积分的乘积向量移项到右端项源项.在半无限边界Γ∞上,从电位与电场的相互关系出发,电位满足的边界条件为

(12)

从而可得边界积分项变分表达式为

(13)

对边界积分项(13)进行单元分析,将所得的结果相加,再扩展成全体节点组成的矩阵或列阵,由全部边界单元相加得

(14)

其中K3为边界系数矩阵.

令(14)式的变分为零,并综合线性方程组(10)可得新的线性方程组:

K1U+K3E=P.

(15)

我们知道,如果以截断边界上的近似场值作为边界条件,那么截断边界造成的边界反射就能得到相应的压制.在直流电阻率法勘探中,总场为一次场和二次场的叠加,二次场由一次场激发,而一次场占主导,因此将一次场代替总场作为截断边界上的边界条件切实可行.取截断边界上电场值E近似等于一次电场值E0(边界处一次电场计算方法见附录),并将其与边界系数矩阵K3的乘积向量移到右端源项中,得到如下线性方程组：

K1U=P-K3E0.

(16)

采用Pardiso_64位求解器对线性方程组(16)进行求解,当源点位置发生改变时,通过计算边界处一次场电场E0得到新的源向量,从而实现多源向量的快速回代求解.

由直流电阻率法三维点源控制方程(1)可知,刚度矩阵K1中每行非零元素之和为零,存在如下等式：

K1c=0,

(17)

其中c为任意常数向量.

因此,线性方程组(16)为病态方程组,求解得到的电位U存在多解,

(18)

其中Ur为真实电位值.

这种多解现象不影响两点之间的电位差计算结果,以及对视电阻率数据的反演结果.当需要计算精确电位值时,可以选取参考点消除U中的常数向量c.参考点为具有相对准确数值的点(如边界处,参考值选为一次场电位值).

4 算例及分析

为了验证本文边界条件算法的计算精度,共选取了三个理论模型进行测试:均匀半空间模型、水平层状介质模型和起伏地形模型.算例中如无特别说明x轴为南北方向,y轴为西东方向,z轴垂直向上,坐标原点位于模型地表中心点.算例中,线性方程组的求解采用Pardiso_64位求解器,测试计算机配置为CPU-Inter Core(TM) i7-4770,主频3.40 GHz,内存32.00 GB;本文边界条件中电位参考点为偶极源中心点(该点电位大多数情况下理论解为0).

4.1 均匀半空间模型

设计电阻率为100 Ωm的均匀半空间模型,如图1所示.其中,模型网格剖分Nx×Ny×Nz为101×101×51,网格总节点个数为520251;水平和垂直方向均采用均匀网格剖分,网格间距为10 m;偶极点电源沿y轴方向布设,供电电流IA=10 A,IB=-10 A,A和B坐标分别为(0,-20,0)和(0,20,0).

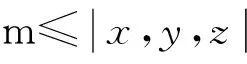
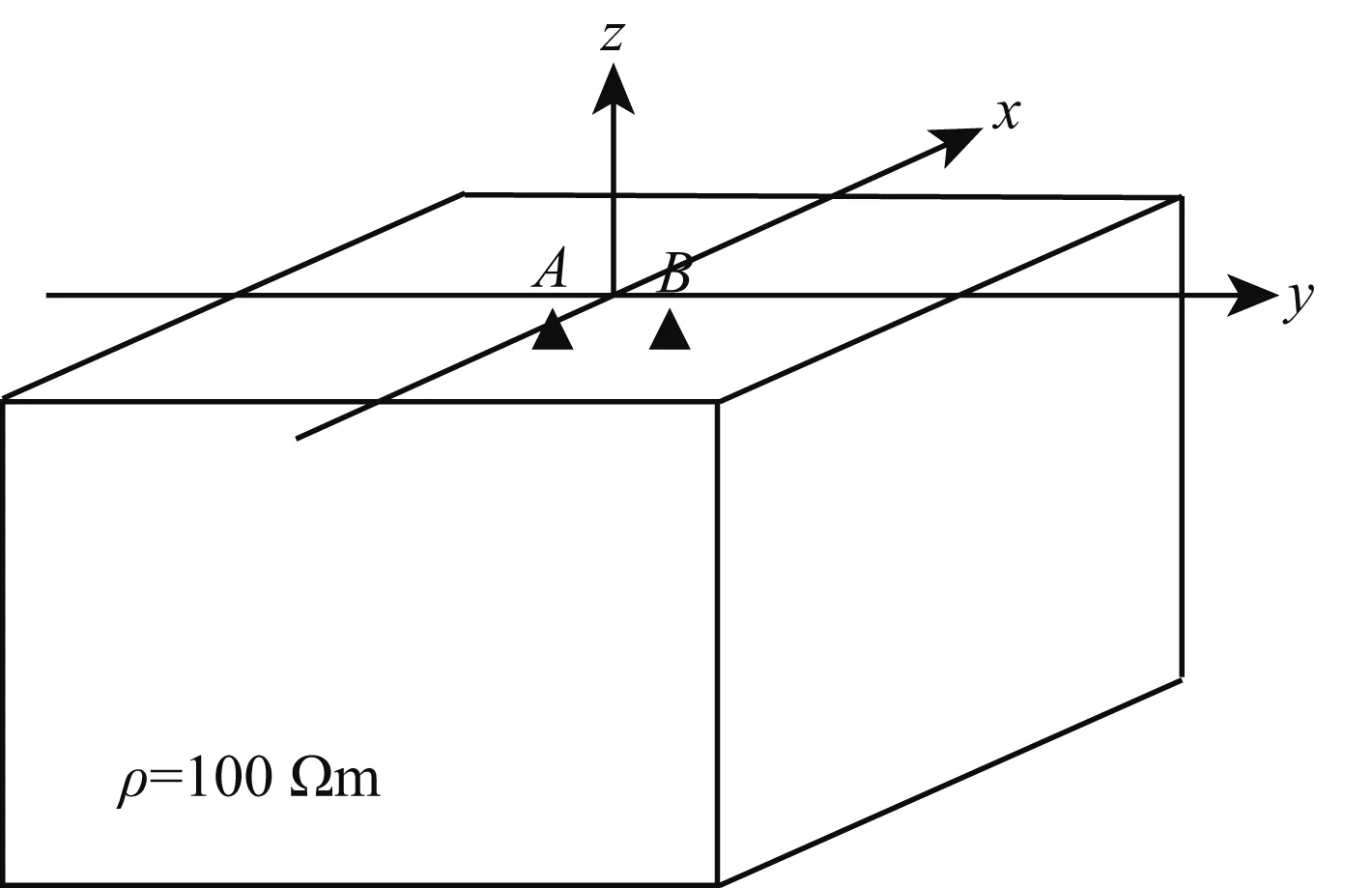
图1 均匀半空间三维模型Fig.1 Homogeneous half space model

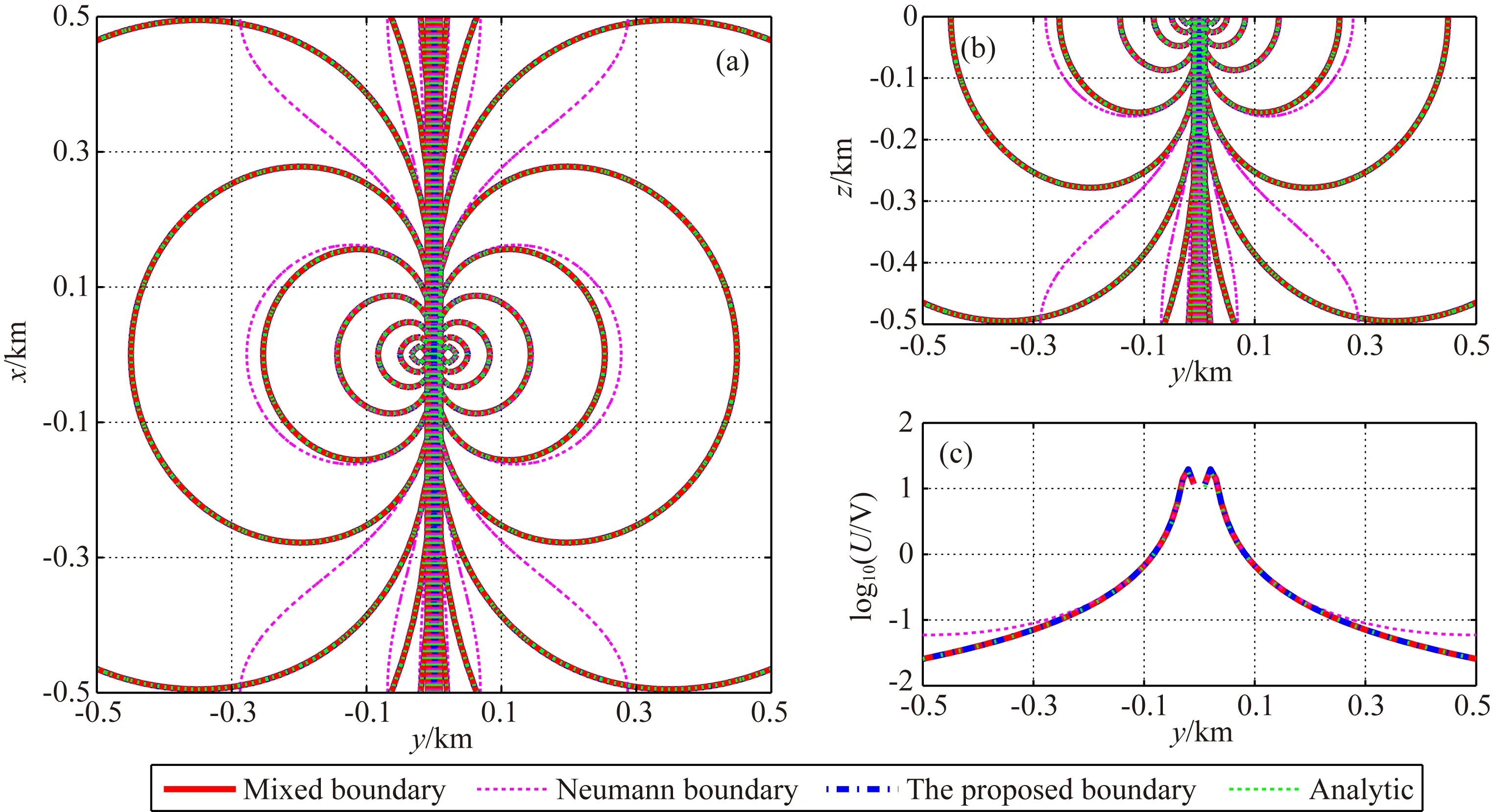
图2 均匀半空间模型数值解和解析解对比红色实线为混合边界条件,粉红色点线为齐次边界条件,蓝色虚线为本文边界条件,绿色虚线为解析解.(a) z=0平面图; (b) x=0 剖面图; (c) z=0, x=0测线.Fig.2 Comparison between the numerical and analytic solutions of the half homogeneous space modelRed solid lines represent the Mixed boundary condition; Pink dotted lines represent the Neumann boundary condition; Blue dashed lines represent the new boundary condition; Green dashed lines represent the Analytical solution. (a) Horizontal plane at z=0; (b) The vertical section at x=0; (c) The observation line at z=0 and x=0.

4.2 水平层状介质模型

如图3所示为水平层状介质两层模型,第一层厚度为100 m,电阻率为100 Ωm;第二层电阻率为1000 Ωm.模型网格剖分Nx×Ny×Nz为101×101×51,网格总节点个数为520251;采用均匀网格剖分,间距为10 m;坐标原点位于地表中心点,供电电流IA=10 A,IB=-10 A,A和B坐标分别为(0,-20,0)和(0,20,0).

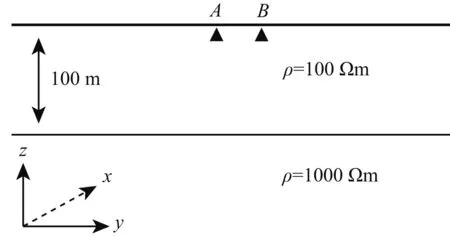
图3 两层层状介质模型Fig.3 Two-layered model

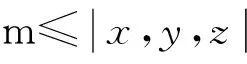
在上述模型边界各增加7个节点,按照1.5倍网格间距进行扩边处理,如图5所示为扩边处理后数值解与解析解对比(去除扩边区域),经过简单扩边处理后,两种边界条件算法在边界区域数值精度都得到了明显的提升,混合边界条件和本文边界条件平均数值误差分别降低到2.784%和0.59%,本文边界条件仍然具有更好的数值结果.

4.3 起伏地形模型

隆起四方台地形模型参数为:地形高50 m,长和宽各160 m,背景电阻率为100 Ωm,在地形正下方置入一个100 m×100 m×25 m的低阻体块,距离顶界面120 m,电阻率为10 Ωm.如图6所示为四方台地形三维示意图,地形位于地表正中央,如图7所示为四方台地形模型在x=0处的电阻率断面图.模型网格剖分Nx×Ny×Nz为115×115×58,网格总节点个数为767050;水平方向采用均匀网格剖分,网格间距为10 m;深度方向初始网格间距为5 m,随着层数的增加网格间距逐渐递增.模型边界各选取7个网格节点按照相邻网格间距的1.5倍进行扩边处理,供电电流IA=10 A,IB=-10 A.

为了研究偶极点电源位于不同位置时截断边界对数值模拟的影响,本文共选取了3对偶极点电源(均位于地表):

第1对偶极源A和B均位于地形左边水平地表上,其坐标分别为(0,-300,0)和(0,-240,0),数值结果见图8a1—8a3;

第2对偶极源中A位于地形左边水平地表上,B位于斜坡地形上,其坐标分别为(0,-170,0)和(0,-110,25),数值结果见图8b1—8b3;

第3对偶极源A和B均位于地形顶端,其坐标分别为(0,-30,50)和(0,30,50),数值结果见图8c1—8c3.

如图8所示为偶极点电源位于不同位置时三种

图4 两层介质模型数值解和解析解对比红色实线为混合边界条件,蓝色实线为本文边界条件,绿色虚线为解析解.(a) z=0平面图; (b) x=0剖面图; (c) z=0, x=0测线.Fig.4 Comparison between the numerical and analytic solutions of the half homogeneous space modelRed solid lines represent the Mixed boundary condition; Blue dashed lines represent the new boundary condition; Green dashed lines represent the Analytical solution.(a) Horizontal plane at z=0; (b) The vertical section at x=0; (c) The observation line at z=0 and x=0.

图5 扩边处理后数值解与解析解对比Fig.5 Comparison between the numerical and analytic solutions for the two-layer model after boundary extensionSolid lines represent the Mixed boundary condition; Blue dashed lines represent the new boundary condition; Green dashed lines represent the Analytical solution.

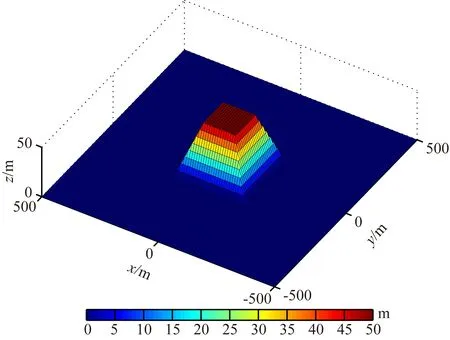
图6 四方台地形三维示意图Fig.6 A 3D view of the square frustum hill model

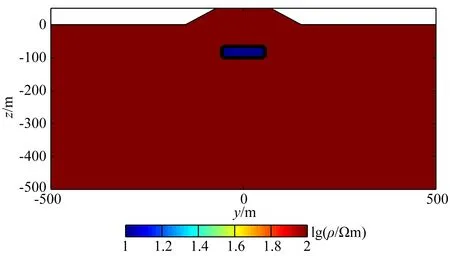
图7 四方台地形模型在x=0处的断面图Fig.7 The vertical section of the square frustum hill model at x=0

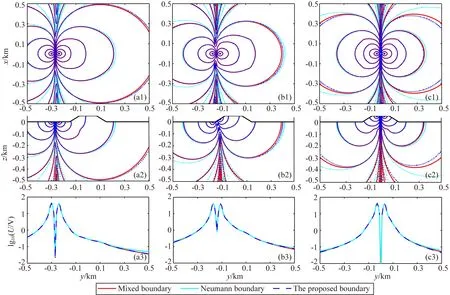
图8 三种边界条件数值模拟结果对比图Fig.8 Comparison of numerical simulation results from three boundary conditions

边界条件(混合边界条件、齐次边界条件和本文边界条件)数值模拟结果在对数区间上的对比图,图8a1,8b1和8c1为地表电位投影平面图,图8a2,8b2和8c2为x=0处电位断面图,图8a3,8b3和8c3为地表过源线电位测线图.图中红线为混合边界条件数值模拟结果,绿线为齐次边界条件数值模拟结果,蓝线为本文边界条件数值模拟结果.在起伏地形条件下,虽然没有解析解作为参考,但是与齐次边界条件相比,混合边界条件数值结果可靠性更高.对比图中三种边界条件数值结果可以发现,在边界区域中,本文边界条件数值结果与混合边界条件非常接近,而齐次边界条件差异很大.

5 结论

本文在多源条件下直流电阻率法有限单元三维数值模拟中,针对目前常用边界条件存在的问题,提出了一种新的近似边界条件方法,该方法联合直接解法实现了快速回代求解,大大提升了数值模拟的计算效率.在理论模型数值算例中,通过对比同等条件下混合边界条件,齐次边界条件和本文边界条件在边界区域的数值精度可以发现:在水平地形条件下,由于能够获得较精确的边界一次电场,本文边界条件数值精度优于混合边界条件;在起伏地形条件下,相比齐次边界条件,本文边界条件与混合边界条件数值结果更接近.鉴于该方法的特点,可以将其推广应用于多源条件直流电阻率法2.5维或其他人工源电磁法数值模拟计算中.

附录：截断边界一次场电场E0的计算

(1) 均匀背景模型

水平均匀半空间模型中,边界M点电位表达式为

(A1)

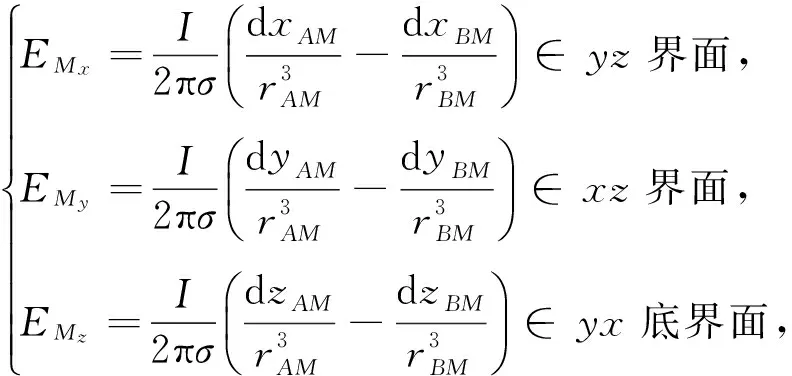
(A2)

式中rAM和rBM分别为点电源A和B到边界M点的距离;dxAM和dxBM为点电源A和B到边界M点所在yz界面的垂直距离,dyAM和dyBM为点电源A和B到边界M点所在xz界面的垂直距离,dzAM和dzBM为点电源A和B到边界M点所在yx底界面的垂直距离.

当模型具有起伏地形时,边界一次场电场E0仍然按照式(2)进行计算.

(2) 层状介质模型

边界处M点电位表达式由数值滤波解法求得,递推表达式参考文献(Li and Spitzer, 2002;李金铭, 2005),滤波系数参考文献(Anderson, 1989; Guptasarma and Singh, 1997).根据电场与电位的相互关系可以求得边界处M点电场分量,基于篇幅的限制,这里给出两层层状介质中边界一次场电场E0的计算表达式:

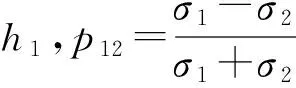
第一层介质中

(A3)

第二层介质中

(A4)

当模型具有起伏地形时,边界一次场电场值E0仍然根据式(A3)和(A4)计算.

致谢 感谢中国石油大学(北京)赵建国教授对本文给予的帮助,并特别对两位匿名评审专家提出的宝贵修改意见表示感谢,最后感谢编辑们的辛苦工作.

Ajiz M A, Jennings A. 1984. A robust incomplete Choleski-conjugate gradient algorithm.Int.J.Numer.Meth.Eng., 20(5): 949-966.

Anderson W L. 1989. A hybrid fast hankel transform algorithm for electromagnetic modeling.Geophysics, 54(2): 263-266.

Arunwan T R, Siripunvaraporn W. 2010. An efficient modified hierarchical domain decomposition for two-dimensional magnetotelluric forward modeling.Geophys.J.Int., 183(2): 634-644.Blome M, Maurer H R, Schmidt K. 2009. Advances in three-dimensional geoelectric forward solver techniques.Geophys.J.Int., 176(3): 740-752.

Davis T A. 2006. Direct Methods for Sparse Linear Systems. Philadelphia: SIAM.

Dey A, Morrison H F. 1979. Resistivity modeling for arbitrarily shaped three-dimensional structures.Geophysics, 44(4): 753-780.

Ellis R G, Oldenberg D W. 1994. The pole-pole 3-D DC-resistivity inverse problem: a conjugate gradient approach.Geophys.J.Int., 119(1): 187-194.

Grayver A V, Streich R, Ritter O. 2013. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver.Geophys.J.Int., 193(3): 1432-1446.

Guptasarma D, Singh B. 1997. New digital linear filters for Hankel J0and J1transforms.GeophysicalProspecting, 45(5): 745-762.

Han B, Hu X Y, Huang Y F, et al. 2015. 3-D frequency-domain CSEM modeling using a parallel direct solver.ChineseJ.Geophys. (in Chinese), 58(8): 2812-2826, doi: 10.6038/cjg20150816.

Huang J G, Ruan B Y, Bao G S. 2003. Finite element method for IP Modeling on 3-D Geoelectric Section.EarthScience—JournalofChinaUniversityofGeosciences(in Chinese), 28(3): 323-326.

Li J M. 2005. Geoelectric Field and Electrical Exploration (in Chinese). Beijing: Geological Publishing House, 136-212.

Li Y G, Spitzer K. 2002. Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite-difference solutions.Geophys.J.Int., 151(3): 924-934.

Liu J W H. 1992. The Multifrontal Method for Sparse Matrix Solution: Theory and Practice.SIAMRev., 34(1): 82-109.

Loke M H, Barker R D. 1996. Practical techniques for 3D resistivity surveys and data inversion.GeophysicalProspecting, 44(3): 499-523.Loke M H, Chambers J E, Rucker D F, et al. 2013. Recent developments in the direct-current geoelectrical imaging method.JournalofAppliedGeophysics, 95: 135-156. Lowry T, Allen M B, Shive P N. 1989. Singularity removal: a refinement of resistivity modeling techniques.Geophysics, 54(6): 766-774.

Nyquist J E, Roth M J S. 2005. Improved 3D pole-dipole resistivity surveys using radial measurement pairs.GeophysicalResearchLetters, 32: L21416, doi: 10.1029/2005GL024153.

Oldenburg D W, Haber E, Shekhtman R. 2008. Forward modelling and inversion of multi-source TEM data. ∥ 78thAnn. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 559-563.

Qiang J K, Luo Y Z. 2007. The resistivity FEM numerical modeling on 3-D undulating topography.ChineseJ.Geophys. (in Chinese), 50(5): 1606-1613. Ruan B Y, Xiong B, Xu S Z. 2001. Finite element method for modeling resistivity sounding on 3-D geoelectric section.EarthScience—JournalofChinaUniversityofGeosciences(in Chinese), 26(1): 73-77. Rucker D F, Loke M H, Levitt M T, et al. 2010. Electrical-resistivity characterization of an industrial site using long electrodes.Geophysics, 75(4): WA95-WA104.

Saad Y. 1996. Iterative Methods for Sparse Linear Systems. Boston: PWS Pub. Co.

Saad Y, Vorst H A D. 2000. Iterative solution of linear systems in the 20thcentury.J.Comput.Appl.Math., 123(1-2): 1-33. Schenk O, Gärtner K, Fichtner W, et al. 2001. PARDISO: a high-performance serial and parallel sparse linear solver in semiconductor device simulation.FutureGenerat.Comput.Syst., 18(1): 69-78.

Schwarzbach C, Haber E. 2013. Finite element based inversion for time-harmonic electromagnetic problems.Geophys.J.Int., 193(2): 615-634. Spitzer K. 1995. A 3-D finite-difference algorithm for dc resistivity modelling using conjugate gradient methods.Geophys.J.Int., 123(3): 903-914.

Tang J T, Gong J Z. 2010. 3D DC resistivity forward modeling by finite-infinite element coupling method.ChineseJ.Geophys. (in Chinese), 53(3): 717-728, doi: 10.3969/j.issn.0001-5733.2010.03.027.

White R M S, Collins S, Denne R, et al. 2001. A new survey design for 3D IP inversion modelling at Copper hill.ExplorationGeophysics, 32(4): 152-155.

Wu X P, Xu G M. 2000. Study on 3-D resistivity inversion using conjugate gradient method.ChineseJ.Geophys. (in Chinese), 43(3): 420-427.

Wu X P, Xiao Y F, Qi C, et al. 2003. Computations of secondary potential for 3D DC resistivity modelling using an incomplete Choleski conjugate-gradient method.GeophysicalProspecting, 51(6): 567-577.

Wu X P, Wang T T. 2003. A 3-D finite-element resistivity forward modeling using conjugate gradient algorithm.ChineseJ.Geophys. (in Chinese), 46(3): 428-432. Wu X P, Liu Y, Wang W. 2015. 3D resistivity inversion incorporating topography based on unstructured meshes.ChineseJ.Geophys. (in Chinese), 58(8): 2706-2717, doi: 10.6038/cjg20150808.

Xiong B, Ruan B Y, Luo Y Z. 2003. 3-D numerical simulation study of DC resistivity anomaly under complicated terrain.GeologyandProspecting(in Chinese), 39(4): 60-64.

Xu S Z. 1994. The Finite Element Method in Geophysics (in Chinese). Beijing: Science Press, 159-172.

Yang D K, Oldenburg D W. 2012. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit.Geophysics, 77(2): B23-B34.

Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids.ChineseJ.Geophys. (in Chinese), 58(8): 2827-2838, doi: 10.6038/cjg20150817.

Zhang J, Mackie R L, Madden T R. 1995. 3-D resistivity forward modeling and inversion using conjugate gradients.Geophysics, 60(5): 1313-1325.

Zhao S K, Yedlin M J. 1996. Some refinements on the finite-difference method for 3-D DC resistivity modeling.Geophysics, 61(5): 1301-1307.

Zhou B, Greenhalgh S A. 2001. Finite element three-dimensional direct current resistivity modelling: accuracy and efficiency considerations.Geophys.J.Int., 145(3): 679-688.

附中文参考文献

韩波, 胡祥云, 黄一凡等. 2015. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812-2826, doi: 10.6038/cjg20150816.

黄俊革, 阮百尧, 鲍光淑. 2003. 三维地电断面激发极化法有限元数值模拟. 地球科学—中国地质大学学报, 28(3): 323-326.

李金铭. 2005. 地电场与电法勘探. 北京: 地质出版社, 136-212.

强建科, 罗延钟. 2007. 三维地形直流电阻率有限元法模拟. 地球物理学报, 50(5): 1606-1613.

阮百尧, 熊彬, 徐世浙. 2001. 三维地电断面电阻率测深有限元数值模拟. 地球科学—中国地质大学学报, 26(1): 73-77.

汤井田, 公劲喆. 2010. 三维直流电阻率有限元-无限元耦合数值模拟. 地球物理学报, 53(3): 717-728, doi: 10.3969/j.issn.0001-5733.2010.03.027.

吴小平, 徐果明. 2000. 利用共轭梯度法的电阻率三维反演研究. 地球物理学报, 43(3): 420-427.

吴小平, 汪彤彤. 2003. 利用共轭梯度算法的电阻率三维有限元正演. 地球物理学报, 46(3): 428-432.

吴小平, 刘洋, 王威. 2015. 基于非结构网格的电阻率三维带地形反演. 地球物理学报, 58(8): 2706-2717, doi: 10.6038/cjg20150808.

熊彬, 阮百尧, 罗延钟. 2003. 复杂地形条件下直流电阻率异常三维数值模拟研究. 地质与勘探, 39(4): 60-64.

徐世浙. 1994. 地球物理中的有限单元法. 北京: 科学出版社, 159-172.

杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827-2838, doi: 10.6038/cjg20150817.

(本文编辑 胡素芳)

An approximate boundary condition for FEM-based 3-D numerical simulation with multi-source direct current resistivity method

ZHANG Qian-Jiang1,2,3, DAI Shi-Kun1,2*, CHEN Long-Wei3, QIANG Jian-Ke1,2, LI Kun1,2, ZHAO Dong-Dong1,2

1KeyLaboratoryofMetallogenicPredictionofNonferrousMetalsandGeologicalEnvironmentMonitoring,MinistryofEducation,CentralSouthUniversity,Changsha410083,China2SchoolofGeosciencesandInfo-physics,CentralSounthUniversity，Changsha410083,China3CollegeofEarthSciences,GuilinUniversityofTechnology,Guilin541004,China

In finite element-based three-dimensional numerical simulation of direct current (DC) resistivity method, applying traditional mixed boundary condition cannot accomplish solving linear equations through recursion due to computation of stiffness coupling with source positions. Currently Neumann boundary condition or infinite element boundary condition is usually used instead. Although rapidly resolving, these two methods reduce the precision of numerical simulation. To realize recursive resolving rapidly and ensure simulation precision, an approximate boundary condition is proposed to implement both fast recursive resolving and precise simulation. The key ideas underlying the method are to separate boundary coefficient matrix coupled with source positions from stiffness matrix so as to make the resultant stiffness matrix independent of source positions. Production of boundary coefficient matrix and primary electric field vectors on the boundary is then transferred to the right hand of linear equations. In doing so only right-hand source items need to be computed when source positions are changed. Synthetic tests show that the numerical simulation precision applying the newly proposed boundary condition is superior to the one using mixed boundary condition in the case of horizontal topography. Also, in the case of rugged topography, the simulation results, compared with the application of neumann boundary, are much closer to those with mixed boundary condition.

Direct current resistivity method; Finite element method; Boundary condition; Numerical simulation

10.6038/cjg20160927.

国家重大科研仪器设备研制专项资助项目(41227803)和国家自然科学基金项目(41574127,41174104,41674075)联合资助.

张钱江,男,1985年生,博士研究生,主要从事地球物理数值模拟与反演成像研究.E-mail:qjz2013@csu.edu.cn

10.6038/cjg20160927

P631

2015-12-08,2016-04-14收修定稿

张钱江, 戴世坤, 陈龙伟等. 2016. 多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件. 地球物理学报，59(9):3448-3458,

Zhang Q J, Dai S K, Chen L W, et al. 2016. An approximate boundary condition for FEM-based 3-D numerical simulation with multi-source direct current resistivity method.ChineseJ.Geophys. (in Chinese),59(9):3448-3458,doi:10.6038/cjg20160927.

*通讯作者 戴世坤,男,1964年生,教授,博士生导师,研究方向为电法勘探三维高效反演成像算法及其实用化软件开发.

E-mail:dskgmes@csu,edu,cn