弧形大悬臂整体桥墩的受力分析

田周松

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

弧形大悬臂整体桥墩的受力分析

田周松

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

介绍了一种弧形大悬臂整体桥墩，其不仅可以为上部预制结构提供支撑，也为地面辅道提供了较大的通行空间，且造型美观。通过杆系模型和实体模型的对比分析，得出了此类桥墩的设计简化计算方法。计算结果表明，通过合理的设计计算，此类桥墩的受力能满足现行规范要求。

大悬臂；桥墩；盖梁；简化计算

0　引言

在城市桥梁建设中，为了加快工程建设进度，缩短施工周期，上部结构往往选择预制结构。同时为了提供更多的通行空间，桥下一般设有地面辅道，需要较大的通行宽度。城市桥梁除了交通功能以外，还是城市的一道风景线，因此城市桥梁还具有很高的景观要求。大悬臂整体桥墩能有效满足上述需要，大悬臂盖梁既能为上部预制梁体提供支撑，同时也为桥下地面辅道提供通行空间，墩柱和盖梁之间的空间弧线整体过渡造型优美［1-3］。

1　设计介绍

图1为某高架的标准桥墩，图2为其施工中的实景照片。盖梁顶宽2.4 m，盖梁中心梁高2.5 m，盖梁根部梁高约2.85 m，盖梁净挑臂长达10.3m。墩身由两根立柱和系梁组成，单根立柱横桥向尺寸为2 m，纵桥向尺寸为1.8 m；系梁中心高为1.2 m，系梁宽1.0 m。墩身和盖梁之间在纵桥向和横桥向采用圆弧过渡。桥墩外侧从立柱底到盖梁顶留有落水管槽口，顶口尺寸为0.26 m，底口尺寸为0.22 m，槽深为0.22 m。

立柱和系梁采用钢筋混凝土结构，大悬臂盖梁采用预应力结构。预应力钢束采用φs15.20高强度低松弛预应力钢绞线，抗拉强度标准值fpk= 1 860 MPa，弹性模量Ep=1.95×105MPa。张拉控制应力为1 395 MPa。钢束立面布置如图3所示，共布置三层钢束，每层6束，N1、N2钢束采用15-13，N3钢束采用15-14。N1、N3在盖梁混凝土龄期达到要求后上部结构架设前张拉，N2在上部结构架设后张拉。

图1　弧形大悬臂整体桥墩构造（单位：mm）

图2　弧形大悬臂整体桥墩现场照片

图3　弧形大悬臂盖梁钢束布置（单位：mm）

2　计算分析

整体桥墩的盖梁按预应力构件设计，立柱按钢筋混凝土构件设计。由于钢筋混凝土立柱的设计计算为常规问题，因此本文主要讨论此类整体桥墩预应力盖梁的受力验算问题。首先采用杆系模型进行简化计算，然后采用实体模型对关键工况进行对比分析，以验证杆系简化模型的合理性和可靠性。

2.1杆系模型分析

杆系分析时，对本文的大悬臂整体桥墩作如下简化：横桥向以立柱外侧位置作为盖梁的支撑点，支撑点至挑臂端部为盖梁的计算挑臂长，盖梁截面不考虑支撑点附近局部倒角；立柱顶部中心线按曲线建模，截面按曲线延伸取值。本文采用桥梁博士V3.3.0建立杆系计算模型（见图4），共58个梁单元。

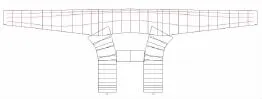
图4　杆系计算模型

经验算，盖梁受力满足设计规范要求，限于篇幅，本文不详述。

2.2实体模型分析

本文采用ANSYS建立三维实体单元模型（见图5）。混凝土实体采用solid92单元模拟；预应力钢束采用link8单元模拟（见图6），预应力与实体之间采用耦合连接，永存预应力荷载采用降温模拟。共103 538个节点，68142个solid92单元，1 098个link8单元。上部小箱梁荷载通过支座垫块施加。

图5　实体有限元模型

图6　预应力单元

为了方便与杆系简化模型进行比较，选择受力明确的成桥恒载工况进行对比分析。盖梁成桥恒载作用下，水平向正应力如图7所示，盖梁顶面整体效应的最小水平压应力储备约为3.2 MPa，最大压应力约为11 MPa，控制截面位于弧线倒角末端附近。同样工况下，采用本文的杆系简化模型，挑臂根部（位于立柱外侧）上缘最小压应力储备为2.9 MPa，下缘最大压应力为10.1 MPa。计算结果说明，采用本文的简化计算方法是基本可行的。

在前述成桥恒载工况的基础上，施加3车道汽车偏载，进一步研究此类大悬臂盖梁的受力安全性。正应力如图8所示，最小压应力储备为1.4 MPa。根据杆系计算结果，非线性温度应力约为2.0 MPa，实体模型结果计入非线性温度影响后最大拉应力为0.6 MPa，与杆系模型中短期组合挑臂根部上缘的0.6 MPa拉应力一致。整体桥墩的主拉应力如图9所示，桥墩内侧圆弧存在1.9 MPa拉应力集中，可通过加强内侧圆弧处的普通钢筋解决。

图7　盖梁恒载正应力（单位：Pa，以拉为正）

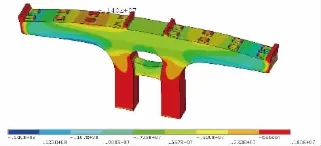
图8　盖梁恒载+汽车荷载正应力（单位：Pa，以拉为正）

图9　盖梁恒载+汽车偏载主拉应力（单位：Pa，以拉为正）

3　结语

本文通过对一弧形大悬臂整体桥墩的计算分析，得出了此类桥墩的杆系简化方法。计算结果表明，通过合理的设计计算，此类桥墩的受力能满足现行规范要求。

［1］全炳欣.桥墩盖梁的设计与计算分析［J］.交通标准化，2013（2）：76-78.

［2］杨秀珍，王勇.大悬臂预应力盖梁设计与应用［J］.广东土木与建筑，2010（1）:49-51.

［3］杨树萍，纪秋吉，朱东.关于盖梁计算模型的探讨［J］.工程与建设，2011（1）:50-51，79.

U443.2

B

1009-7716（2016）06-0115-02

2016-02-22

田周松（1984-），男，安徽安庆人，硕士，工程师，研究方向为桥梁设计与结构分析。