木梁拼接截面碳纤加固抗弯承载力

黄龙田，霍文斌，刘　玫

（1.广东省建筑设计研究院，广东 广州　510010；2.广州市公用事业规划设计院，广东 广州　510230）

木梁拼接截面碳纤加固抗弯承载力

黄龙田1，霍文斌1，刘玫2

（1.广东省建筑设计研究院，广东 广州510010；2.广州市公用事业规划设计院，广东 广州510230）

木结构矩形截面承重梁跨中拼接，拼接点没有任何连接构造，基本上失去了抗弯能力，出于外观的考虑，采用碳纤维片材加固，对此，导出拼接木梁极限抵抗弯矩公式。矩形截面拼接木梁用碳纤加固后弹性受力阶段抗弯承载力比原材全截面计算的承载力可提高25%。界限破坏时抵抗弯矩比原材全截面计算的承载力提高约30%，提高值取决于木材受压比例极限与屈服极限之比，即由木材性质所决定。

木结构；叠合梁；拼接截面；碳纤加固计算公式；抗弯承载力

0　引言

数座景观木亭承重叠合梁，矩形截面，由于设计或施工的原因，梁的跨中截面由方木拼接但没有任何连结措施（见图1），梁已失去抗弯承载能力。

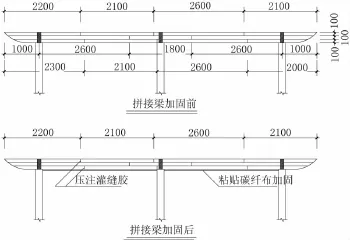
图1　拼接梁加固前后示意图（单位：cm）

加固方案比选结果采用碳纤维片材加固，为此要求探讨和评估单根拼接木杆件经粘贴碳纤维片材加固后构件的抗弯承载力。

设定的前题是：竖向拼接面仅承受弯曲压应力，拼接面木纤维不参加抗拉作用，弯曲拉应力完全由碳纤布所取代。以下的论述是对单根拼接木杆件而非对叠合梁，具体的加固措施另文叙述。

1　加固后梁的弯曲破坏类型

可能的破坏类型有：

（1）受压区木材顺纹挤压破坏；

（2）碳纤布拉断；

（3）碳纤布剥落（含粘贴区木纤维破坏）

因后两种类型是可控的，仅对第一种破坏类型进行计算公式的分析推导。

2　基本假设

拼接截面压注灌缝胶后受压区可承受压应力，不考虑受拉区粘合后的抗拉作用，截面下缘粘贴的碳纤维布作为抗拉元素；碳纤维布受拉时的应力与应变是线性关系。承载力计算公式推导的基本假设是：

（1）梁受弯后截面应变仍保持平面；

（2）碳纤的应力应变关系为线性，即

σf=Ef×εf

（3）拼接的截面只传递压应力，不考虑受拉区粘合后木材的抗拉作用；

（4）碳纤布中心到梁顶的距离等于梁高；

（5）木材的应力应变关系：可通过柱形木试件测试取得［1］，现按文献资料［2］选取松木的应力应变关系曲线（见图2）作为分析推导的基础。

图2　木材（松木）顺纹受压的应力应变实验曲线

图3　木材（松木）顺纹受压的应力--应变曲线（简化）

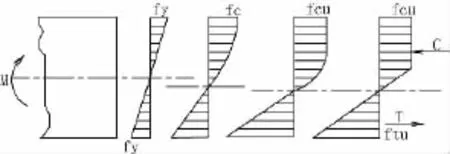
图4　木构件受弯各工作阶段

截面应力-应变关系式：

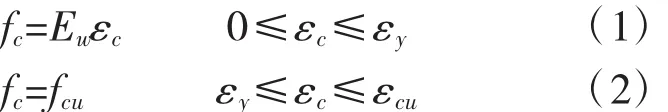
式中：fc为木材压应力；εy为木材比例极限压应变；εcu为木材极限压应变；εc为木材压应变；Ew为木材受压弹性模量。

3　弹性受力阶段截面抗弯承载力分析——实用计算方法

设定受弯构件截面应力在比例极限应力以内，木构件近似看作弹性体，外力消失后变形恢复。

弹性受力阶段截面的应力分布：受压区应力在比例极限以内，截面压应力应变对截面形心的距离成正比，中和轴以上压应力呈直线分布，拼接的木梁，中和轴以下截面不考虑抗拉应力，下缘碳纤拉应力与下缘应变成正比，见图5。

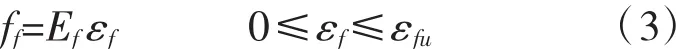
式中：εfu为碳纤极限拉应变；εf为碳纤拉应变；Ef为碳纤弹性模量；ff为碳纤拉应力。

图5　弹性受力阶段截面应力分布图

设木材比例极限压应力为fy，受压区压力的合力为C，合力到截面上缘距离为yc。

C=0.25 bhfy，b为矩形截面宽度。

木结构设计规范［4］对受弯构件抗弯承载力验算采用，fm为木材抗弯强度设计值是基于截面应变保持平面的假定和弹性体的假定，规范对fm的取值，已隐含了抗力的分项系数并经过调整，因此可按规范取fy=-fm，则受压区压应力合力C

C=0.25 bhfm

上式可改写为

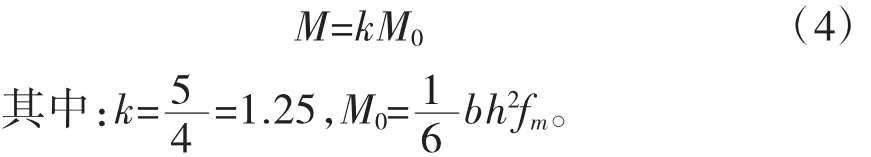
M0为按规范计算矩形截面梁的抗弯承载力。由∑x=0EfεfAf=C

EfεfAf=0.25bhfm

Af=0.25bhfm/Efεf

计算碳纤面积时取 εf=εY

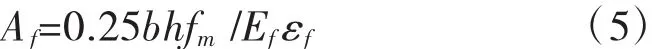
由式（4）得出，矩形拼接截面木梁用碳纤加固后抗弯承载力比原材全截面计算的承载力提高25%。条件是按式（5）计算碳纤面积，碳纤应变按小于等于木材受压比例极限应变取值，木材抗弯强度按规范取值。

木材顺纹受压应变的比例极限εy木结构规范没有作出规定。木材是生物材料，不同种类差异很大，比例极限可通过实验数据取得，按文献资料［2，5，6］对于承重结构的木材，建议可取0.002～0.004，取下限用于确定碳纤用量时将偏向安全。

对于非拼接的全截面抗弯构件加固，也可采用上述公式计算，因为没有考虑木纤维的抗拉作用，计算结果偏于安全。

4　塑性受力阶段截面抗弯承载力分析——界限破坏弯矩计算

4.1受压区塑性变形阶段的应力应变关系

木材顺纹压应力超过比例极限时，木纤维受压屈曲，破坏时试件表面出现皱折，并呈现明显的塑性变形特征曲线［5］。

当弯矩继续增大，受压区出现塑性变形，极限状态时，压应变εc=εcu。如果碳纤维布也同时达到最大拉应变εf=εfu，此时受压区的高度定义为界限受压高度，对应的弯矩定义为界限破坏弯矩。根据图3的应力应变曲线，可以建立图6的应变和应力图形。

图6　应变和应力图

4.2界限破坏时抵抗弯矩计算

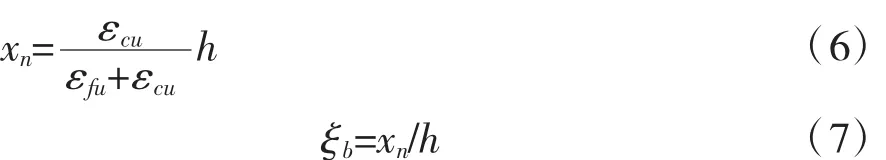
ξb：相对界限高度

取 εcu=0.008。

按加固规范［7］碳纤极限应变取εfu=0.014，则ξb=0.364。

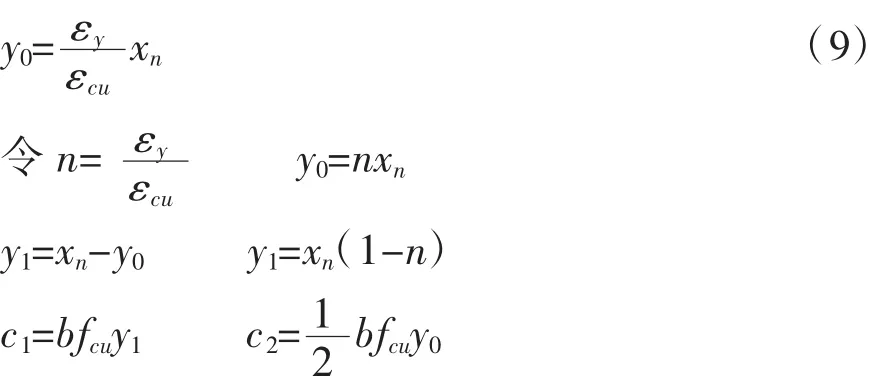
受压区合力c=c1+c2

合力C对受压区上缘静矩S：

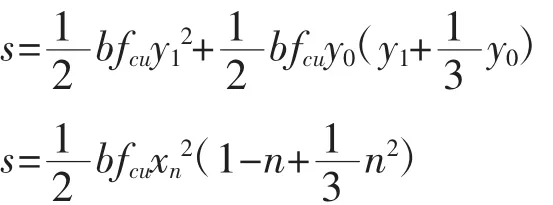
合力C重心到上缘距离yc

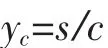
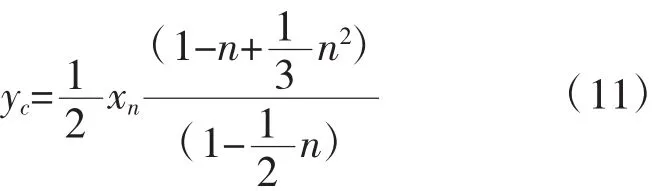
合力C对碳纤合力点取矩，则界限破坏时抵抗弯矩为：

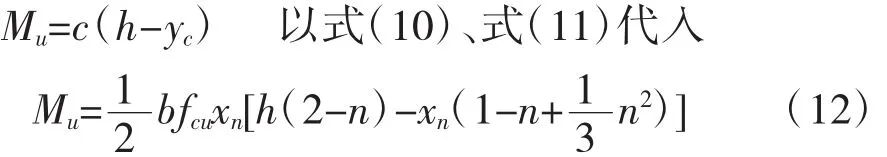
以式（7）代入

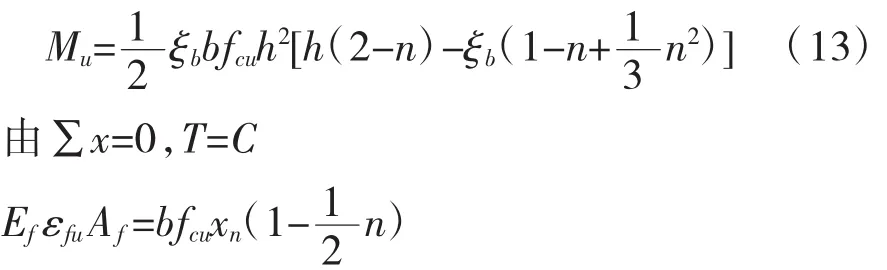
以式（7）代入

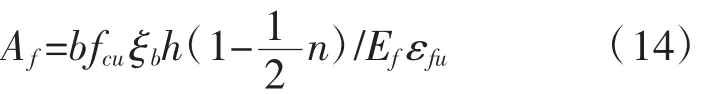
4.3小结

从以上公式可得出以下结论：

（1）当截面尺寸已定，碳纤极限应变按规范取值，界限破坏时抵抗弯矩取决于，即取决于木材受压比例极限与屈服极限之比，由木材性质所决定。

（2）碳纤加固承载力提高的限值：式（13）可改写为：

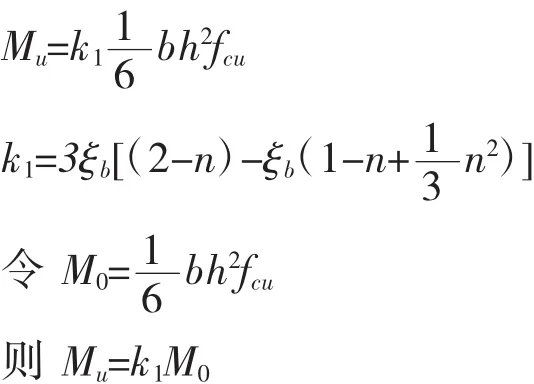
M0形式上相当于普通木结构计算的抗弯承载力的公式，但强度的取值为顺纹抗压极限强度计算值fcu，k1可视为粘贴碳纤后承载力提高系数。k1可制成计算表格备查（见表1）。

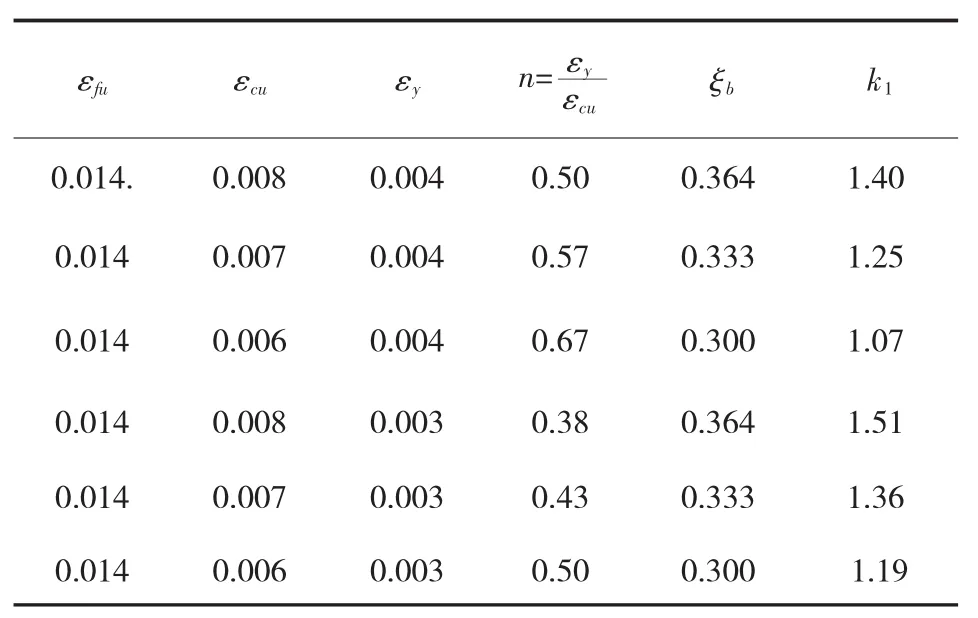
表1　k1系数表

k1平均值为1.30，可认为木梁碳纤加固后界限破坏时抵抗弯矩比原材按全截面计算的抵抗弯矩平均提高30%.

5　工程应用

计算理论用于某五星级宾馆中庭的六座景观木亭加固，经6 a的时间考验，使用正常，效果良好。

［1］GB 50329-2002，木结构试验方法标准［S］.

［2］А.П.巴甫洛夫.木结构与木建筑物［M］.上海:上海科学技术出版社，1961.

［3］龚伟，李希钧，刘励诚.钢结构与木结构［M］.北京:中国建筑出版社，1988.

［4］GB 50005-2003，木结构设计规范［S］.

［5］潘景龙，祝恩淳.木结构设计原理［M］.北京:中国建筑工业出版社，2009.

［6］广西大学.木材学［Z］.

［7］CECS 146：2003，碳纤维片材加固混凝土结构技术规程［S］.

［8］GB 50367-2006，混凝土结构加固设计规范［S］.

TU366.2

B

1009-7716（2016）06-0316-03

2016-02-23

黄龙田（1976-），男，湖南邵阳人，高级工程师，从事路桥设计工作。