一种适用于砂性土地层盾构隧道地表沉降理论预测方法
潘涛
(上海隧道工程有限公司,上海市200082)
一种适用于砂性土地层盾构隧道地表沉降理论预测方法
潘涛
(上海隧道工程有限公司,上海市200082)
盾构法隧道施工广泛应用于城市公路、地铁、给排水、电力等隧道工程施工中。但是,由于施工工艺质量及周围的施工环境和土层特点,施工引起的地层位移是不可能完全消除的。如果影响过大,势必会引起地表的沉降隆起超限,严重情况会导致周围建筑物倾斜倒塌和构筑物变形。在现有的沉降理论预测方法中选择适合于砂性土地层盾构施工引起的地表沉降预测方法,并在该方法基础上进行改进,得出砂性土地层特有的不同推进参数下盾构隧道施工引起的地表沉降理论预测方法。
砂性土地层;推进参数;地表沉降
0 引言
盾构法隧道施工广泛应用于隧道施工中。由于施工技术工艺质量及周围的施工环境和土层特点,施工引起的地层位移是不可能完全消除的。
在地表沉降预测方面,国内外开展了大量的研究,积累了很多方法,主要可以归纳为:经验法、室内模拟实验法和数值模拟法等类型[1.2]。其中,经典的地表沉降槽模型为Peck横向地表沉降槽。他引入类似倒正态分布曲线的数学模型,在沉降预测理论研究方面有着重要的指导意义。其他科研工作者在其基础上引入多项参数,在不同的数学方法上验证Peck公式的可行性,同时也提出了更加精确的沉降模型。但是,许多沉降模型都受实际环境的影响,或者多用于实验室理论验证。
砂性土地层特点特殊,对于易坍塌的砂质土、含黏土少的砂、砂砾等地层,地表沉降控制是施工质量控制的重要指标之一。本文依托郑州城郊铁路08标项目工程,结合其特有的施工砂性土地层特点,在原有的地表沉降预测数学模型基础上,引入盾构推力,推进速度等参数,将横向沉降槽扩展为纵横相结合的区域性沉降槽,得出砂性土条件下盾构推进区域的局部沉降槽预测模型。
1 地表沉降预测模型
1.1Peck法沉降预测
早在1969年,Peck[3]提出地层损失的概念和估计隧道施工引起地面沉降的实用方法。他的理论基于大量的地表沉降数据实测分析,最后得出近似于正态分布曲线的沉降槽(见图1)。在后来实际应用中,大量的研究者在Peck的基础之上对预测模型进行改进,其预测公式为:式中:S(X)为地表距离隧道中心线处的地表沉降;Smax为隧道中心线上的地表沉降;i为地表沉降槽宽度系数;Vs为单位长度地表沉降槽体积;H为覆土厚度;为土体内摩擦角加权平均值。
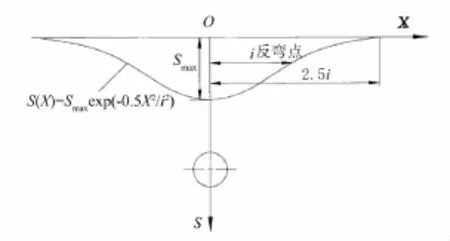
图1 地表横向沉降槽示意图
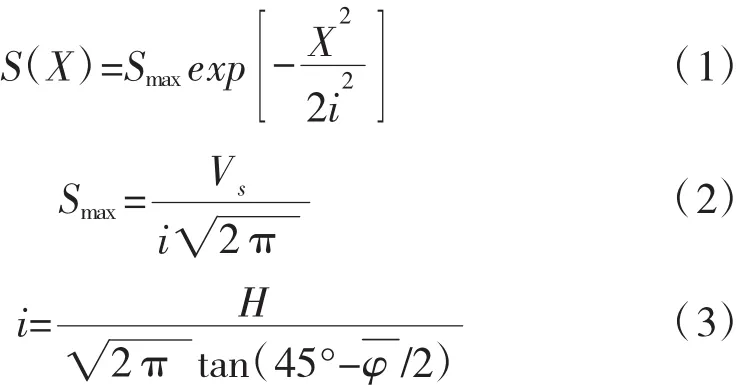
从公式(3)可以看出,地表沉降槽宽度系数i与覆土厚度H成正比关系。代入公式(1)可以知道,地表沉降量与隧道覆土厚度呈一定的函数关系,即理论上覆土厚度越大,沉降量越小。
当然,Peck沉降预测法倾向于实验室研究地表沉降,在实际的施工中,需要对此进行修正,也会依据不同的施工环境进行参数改正,如解析法、数值模拟法和镜像法[4]等,本文不一一赘述。
1.2修正沉降预测数学模型
盾构推进过程中引起的地表沉降往往与其他因素有关,例如推进速度、推力、刀盘扭矩和地质条件等,同时与同步注浆等施工工艺也有很大的关系。本文所介绍的数学模型主要以盾构的推进参数为依据,在原有的数学模型基础上,引入盾构推进速度和推力两大因素进行探讨,构建砂性土地层不同推进参数下引起的地表沉降模型。
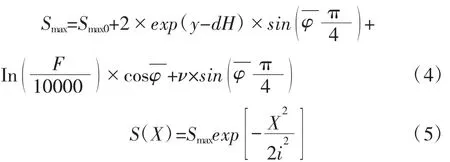
式中:Smax0为隧道中心线上的地表沉降;y为纵向距离刀盘切口距离;X为横向距离隧道中心线距离;dH为盾构刀盘至盾构距离;F为盾构推力,kN;ν为盾构推进速度,cm/min;S(X)为地表沉降量。
1.3地表沉降槽宽度系数
在模型中,假定沉降理论模型为楔形槽,如图2所示。则隧道起拱点与地面沉槽宽度边缘点连线的水平仰角β为地层影响角[5]。
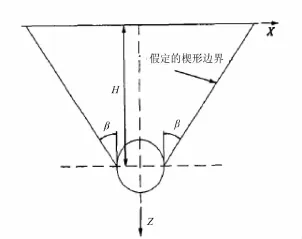
图2 地表沉降模型
中南大学杨小礼[5]认为:粘土地层中地层影响角β随着地质条件的变化而变化。在粘性土中,软粘土的沉降宽度系数(0.6~0.7)要大于硬裂隙粘土的地表沉降宽度系数(0.4~0.5)。在实验的基础之上,得出沉降模型的不同地层影响角β的建议值,如表1所列。

表1 不同地层条件下地层影响角β建议值一览表
表中,为土体内摩擦角加权平均值,基于上文提到的地层影响角在不同地层的取值范围,可取砂性土地层土体内摩擦角加权平均值为45°。
1.4地表沉降预测模型
改正后的数学模型将单一的横向沉降槽转化为区域性沉降槽,可以在已知覆土厚度、盾构推力、推进速度等参数条件下,预测盾构机所在区域的局部地表沉降情况,如图3所示。
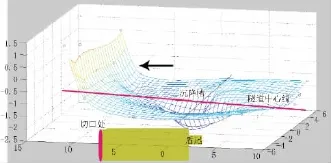
图3 改正后地表沉降槽模型示意图
改正后的数学模型并不可以预测大范围地表沉降,距离盾构越近,预测值可信度越高。一般采用距离盾尾约10 m处的沉降点数值作为模型构建基础。
2 实例分析
本文在从改变模型参数得到理论沉降值与实测值进行对比,验证模型的可行性及适用性。本文的数据来源为郑州市南四环至郑州南站城郊铁路工程一期工程08标段地表沉降数据。08标段位于一期工程规划线路最南端,区间线路主要下穿机场二期规划用地和机场捷运区间。盾构穿越地层主要以粉砂、细砂为主,隧道埋深在14 m~21 m。
本文数据分析工具为Matlab R2010b版本,通过编程构建数据计算模型,引入不同变量值进行模型构建,并输出三维网格图。监测点布设纵向间距为4 m,共布设5个断面,横向分别以3 m,2 m,2 m,2 m,3 m布设6个监测点(见图4)。
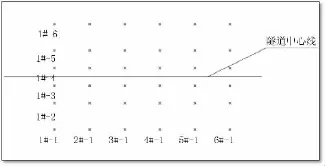
图4 改正后地表沉降槽模型监测点布设示意图
2.1不同推力下的沉降模型
盾构推力是影响切口处地表沉降的重要因素之一。推力过大会引起地表的隆起,推力过小会引起地表的超限沉降。推力值取13 500~15 000 kN之间,计算结果见表2所列。

表2 不同推力下地表沉降槽模型沉降量一览表
由表2统计可以看出:推力增大会引起地表的隆起,沉降槽在盾构切口处呈隆起状态,在盾尾处沉降值最大。
2.2不同推进速度下的沉降模型
不同的推进速度对沉降槽有相应的影响,从沉降槽公式(4)可以看出,沉降量会随着推进速度的变化而变化,通过沉降槽公式计算沉降数据如表3所列。
2.3理论计算与实测数据
2.1节和2.2节主要讨论了在不同推力和推进速度的情况下沉降槽预测情况,总体看来,沉降槽沿推进方向沉降量逐渐增大,在盾尾处沉降量达到最大,在切口附近,地层由于刀盘的推力作用,地表呈轻微隆起状态。根据模型计算和实测值进行对比,得出的数据列于表4。
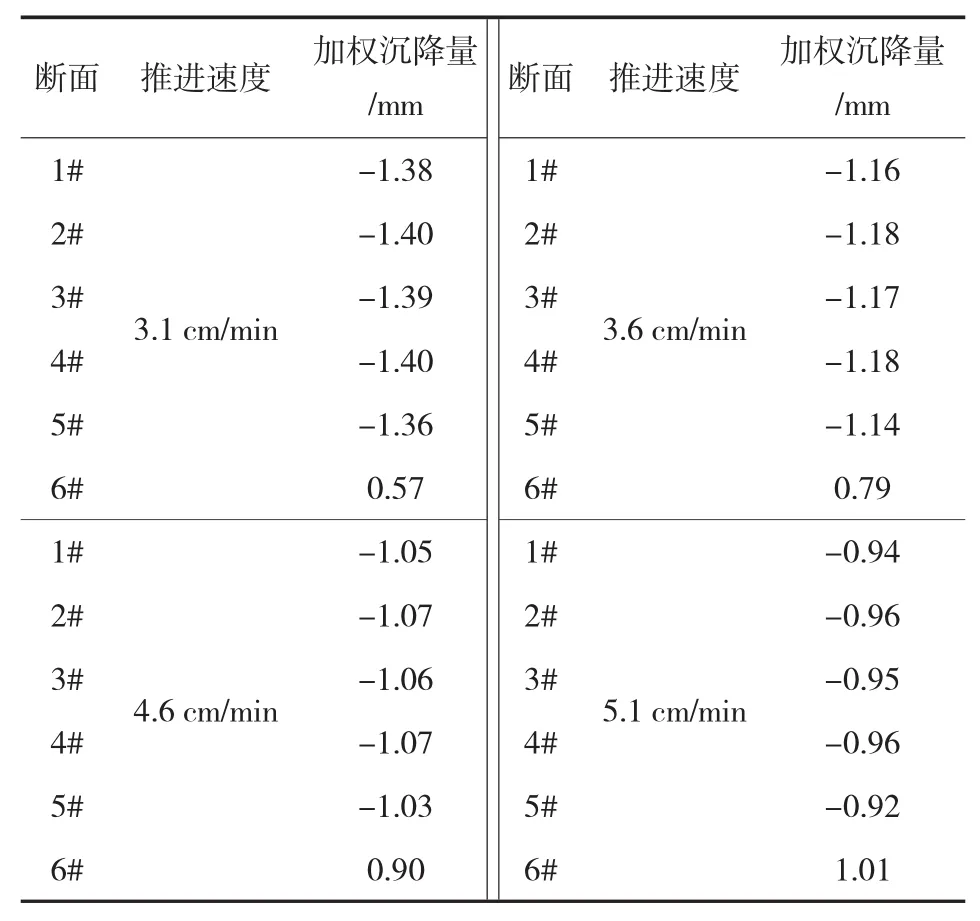
表3 不同推进速度下地表沉降槽模型沉降量一览表
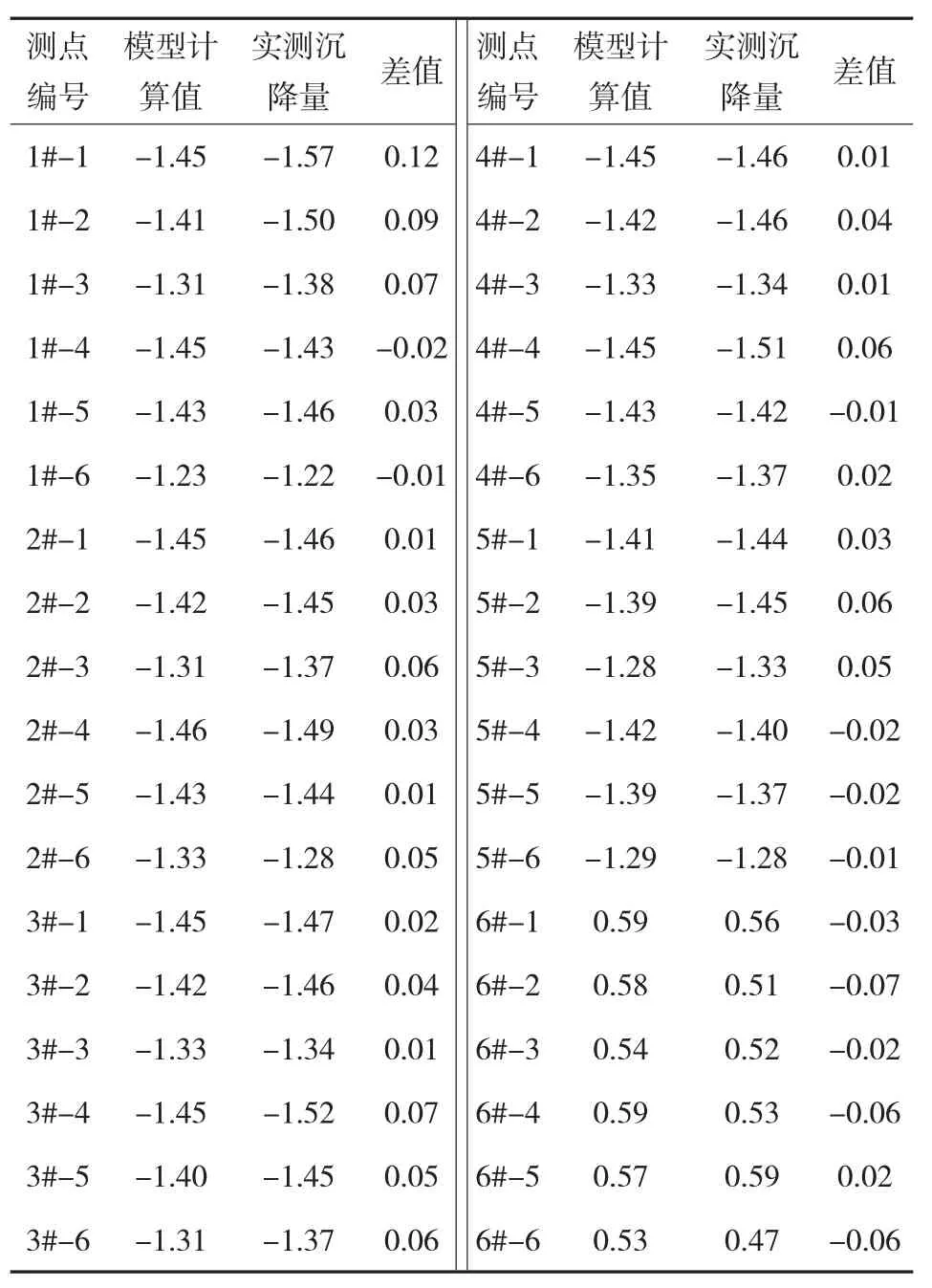
表4 沉降模型理论计算值与实测值对比表 mm
从表4可以看出,理论计算模型与实测数据差值最大为0.12 mm,在实际应用中,可以利用理论模型做相关的地层沉降分析,为施工提供相应的指导建议。
3 结 论
地表沉降预测在实际操作中很难控制,诸如地质条件因素、施工参数因素、后期注浆维稳因素
451
A
1009-7716(2016)06-0319-03
2016-02-23
潘涛(1985-),男,江苏人,工程师,项目总工程师,从事城市轨道交通工程和地下工程技术研究工作。

