问题驱动课堂教学 经历促进学生发展——教学“确定起跑线”一课的研究和实践
广东广州市海珠区宝玉直实验小学(510250) 熊国娟
问题驱动课堂教学经历促进学生发展——教学“确定起跑线”一课的研究和实践
广东广州市海珠区宝玉直实验小学(510250) 熊国娟
“综合与实践”活动课对教师而言比一般的课堂教学有着更高的要求,不仅在知识上需要更丰富、更立体,要具有发展的眼光、培养的意识,而且在课堂中要善于“隐退”,这种“退”是为学生的“进”做铺垫的,并在必要时发挥帮助、促进等作用。
综合与实践起跑线教学设计反思 问题发展
“综合与实践”是《数学课程标准》(2011版)提出的四大课程内容之一,它要求的课时数虽然不多,但设计并实施该课程的意义重大,承载着重要的教育价值。但是,“综合与实践”活动课和一般的数学课到底有什么样的区别?怎样实施才能真正实现“综合与实践”活动课的教育价值?带着困惑与问题,我们借助“确定起跑线”这一具体的教学进行研究和实践。
一、学习理论后的初步体会
《数学课程标准》(2011版)指出:“‘综合与实践’是一类以问题为载体,以学生自主参与为主的学习活动。”从“问题”“自主参与”等关键词可以看出,在“综合与实践”活动课中,应以问题为主线,贯穿教学活动的始终,并围绕着问题的发现、提出、分析、解决这几个环节,促进课堂教学的顺利进行。同时,在经历和体验的过程中,学生将体会数学与外部世界的联系、数学内容之间的联系,积累数学活动经验,发展实践能力和创新意识。这样的教学,让学生的学习从课内走向课外、从表面走向深层、从单一走向多元。和一般突显数学味的数学课相比,“综合与实践”活动课的教学还应该突出综合性和实践性。所以,“综合与实践”活动课的教学应该有别于常规的数学课。
《数学课程标准》(2011版)在对第二学段“综合与实践”的要求中指出:“教师应结合实际情境,引导学生体验发现和提出问题、分析和解决问题的过程。”那么,如何才能让学生发现隐藏在生活中“确定起跑线”这一数学问题呢?如何才能让学生充分经历“选题——开题——做题——结题”的过程,实现“综合与实践”活动课的数学教育价值?
二、研读他人教学设计后的思考
通过研读搜集到的教学设计,我们发现这些教学设计有以下共同点。
1.重视问题的引领,让学生在生活情境中经历发现和提出问题的过程
《数学课程标准》(2011版)中指出:“在‘综合与实践’中,给学生自己发现和提出问题、独立思考、归纳猜想等提供更大的空间。”发现体育中“确定起跑线”问题原来是数学问题,需要学生在经历中体验、在体验中构建,且这种体验必须来自脑、口、手的充分参与,是需要一定时间做保障的。所以,我们决定将这一环节移至课前,让学生分小组进行,这样既能保证学生真的有所发现,又能让学生带着思考进入课堂,提高课堂教学效率。
2.关注学生经历活动的整个过程
《数学课程标准》(2011版)在对第二学段“综合与实践”的要求中指出:“在给定目标下,教师应引导学生感受针对具体问题提出设计思路、制定简单方案的解决问题的过程。”因此,我们认为“确定起跑线”的教学重点不应该是仅让学生找到确定起跑线的不同方法,最终构建确定起跑线的最优数学模型上,还应该给予足够的时间,让学生通过猜测、讨论等活动,分析确定起跑线和什么有关等问题上。课堂教学中,学生充分经历分析问题这一过程,能更有效地积累数学活动经验,提升应用意识与创新意识。
3.尊重教材的编排
教材基本上都是把如何确定400米跑起跑线作为探究的重点,把200米跑起跑线的确定作为巩固练习或拓展题出现。学生根据已有经验,知道内外两圈跑道长度不同是由经过的弯道造成的。如果从经过一个弯道的200米跑起跑线先开始探究,在理清了起跑线位置和一个弯道、道宽等之间的关系后,再让学生想象经过两个弯道400米跑、甚至800米跑起跑线的位置,这样教学会不会更加水到渠成?
4.体现综合性
很多教学设计都体现了综合运用图形的认识、测量、数据调查等方面的数学知识和技能解决问题的过程,计算器也被很多教师请进了课堂。对于六年级的学生来说,虽然会使用计算器,但在实际生活中运用较少,所以对计算器有些键的使用还是生疏的。因此,课堂上让学生使用计算器进行计算,会不会出现计算速度反而更慢的情况呢?鉴于这种担忧,我们在第一次试教时注重观察学生使用计算器的情况,结果发现不少学生使用计算器计算的时候都不喜欢在纸上先列式,而是一边想一边按键,导致思维出现停顿时手也出现了混乱,如此反复,反而耽误了更多的时间。因此,我们舍弃计算器,要求学生用π值表示结果,突出学生活动经验的积累。
三、我们的教学设计
基于以上思考,我们经过反复的试教,最终确定了以下的教学设计。
1.激活经验,发现和提出问题
(1)屏幕出示课前研究任务单。
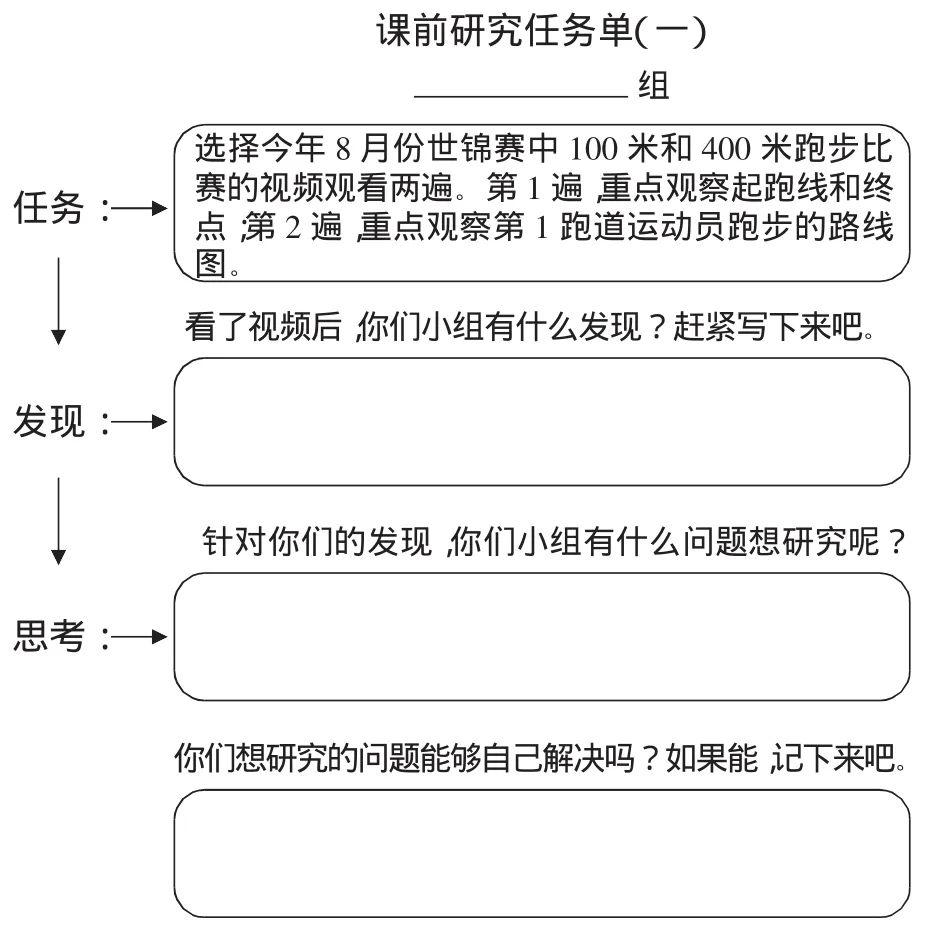
①观看跑步比赛的视频后,你们小组有什么发现?
②你们的发现,有没有让你们产生一些思考?
③通过小组集体的力量,你们已经解决了哪些问题?
(2)选定课题:确定起跑线。
2.启迪智慧,分析和解决问题
(1)观察跑道结构,明确什么是直道、什么是弯道、什么是道宽,知道跑道间的道宽一样、所有直道的长度都相等、两个半圆形跑道合在一起就是一个圆。
(2)想一想:先研究几百米赛跑的起跑线比较合适?
师(出示200米跑道示意图):要想确定起跑线在哪里,需要知道两条跑道相差多少,起跑线就要向前移动多少。
(3)商讨、制订活动方案。
①讨论:怎样确定第2跑道的起跑线应该向前移多少米?
预设:外跑道长度-内跑道长度=前移米数,或外弯道长-内弯道长=前移米数。
②说说:你们需要老师提供怎样的帮助?(需要相关数据)需要哪些数据呢?为什么需要这些数据?(师根据学生的需求在跑道图中适时出示相关数据:直道85.96m,内圈半径36.3m,道宽1.25m)
③师(出示表1):为了方便我们算完之后进行观察和发现,你觉得哪些数据是我们算出来之后需要记录的?(学生商讨后完善记录单,如表2)
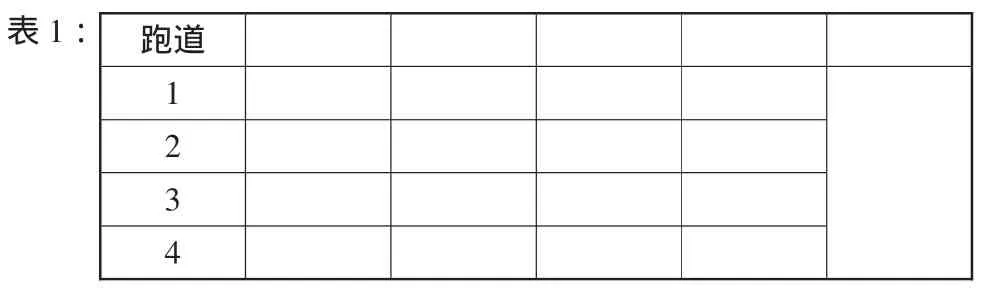
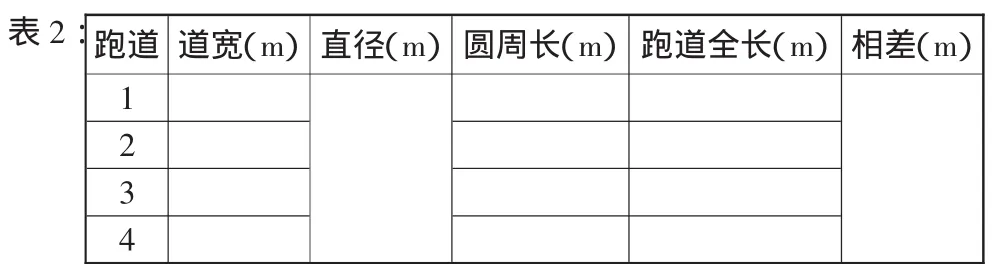
(4)动手实施活动方案。
①各小组根据制订的方案,先分别算出第1跑道和第2跑道、第2跑道和第3跑道、第3跑道和第4跑道的相差数,再填好记录报告单。(为了方便,结果用π表示)
②分小组汇报。
(5)找规律。
①讨论:为什么相邻跑道前移米数都是相等的?如果外面再多加几条跑道,结果还会一样吗?
小结:跑200米,经过一个弯道和一条直道,直道总是相同的,经过弯道的时候内外跑道距离产生差异,但道宽相同,所以相邻跑道间的相差数总是一样的。
②课件演示确定200米跑起跑线位置的动态前移。
3.拓展延伸,提出新问题
(1)讨论:在400米跑道上进行400米赛跑,每道跑道的起跑线应该前移多少米?怎样想的?
(2)比较:都是在400米的跑道上,为什么400米跑起跑线外圈要比内圈移动2.5π米,200米跑起跑线外圈比内圈只要向前移动1.25π米呢?
小结:200米跑经过1个弯道,相差数就是1个道宽乘π;400米跑经过2个弯道,相差数就是2个道宽乘π,所以说起跑线的确定跟经过的弯道数量有关。
(3)想象。
①在400米跑道中,跑800米,经过几个弯道?起跑线要前移多少米?
②让学生观看800米赛跑的视频,重点关注抢道现象。
小结:800米赛跑虽然经过4个弯道,但是影响起跑线确定的只有1个弯道,所以确定起跑线还跟比赛规则有关。
(4)拓展。
师(出示200米环形跑道):如果只给出一个数据,你想要什么数据就能很快确定200米赛跑的起跑线呢?
4.学习回顾,积累经验
师:回顾一下,这节课我们做了什么?今天你最大的收获是什么?
5.课后延伸(略)
……
四、反思
在教学“确定起跑线”一课中,我们力求激活学生的思维,让他们真正成为学习的主体。课堂上,问题让学生自己发现和提出,方案让学生自己制定和实施,经验让学生自己反思和积累,这样不仅使学生真正理解所学知识,而且积累了数学活动经验,实现“综合与实践”活动课的教育价值。
此外,在对“确定起跑线”一课教学研究的过程中,我们感受到“综合与实践”活动课对教师比一般的课堂教学有着更高的要求,不仅在知识上需要更丰富、更立体,要有发展的眼光、培养的意识,而且在课堂中要善于“隐退”,这种“退”是为学生的“进”做铺垫的,并在必要时发挥帮助、促进的作用。
(责编杜华)
G623.5
A
1007-9068(2016)32-018

