数学思想方法在数学解题中的应用研究

江苏盐城幼儿师范高等专科学校（224000） 臧亚东

数学思想方法在数学解题中的应用研究

江苏盐城幼儿师范高等专科学校（224000） 臧亚东

小学数学解题中涉及多种数学思想方法，重视数学思想方法的有效渗透和灵活运用，有助于深化和巩固学生对知识的理解，提升学生的思维品质，增强学生的解题能力，培养学生良好的数学素养。对此，教师要引领学生把握转化思想，变换形式，化繁为简；注重整体思想，纵观全局，化难为易；巧用分类思想，各个击破，积零为整。

数学思想方法数学解题应用

数学思想方法是人们对数学知识的本质认识，是分析和解决数学问题的指导方法和基本策略。引导学生正确理解、掌握以及灵活运用数学思想方法，可促使学生领会数学真谛，发散数学思维，开阔解题思路，提高分析及解决问题的能力。

一、把握转化思想，变换形式，化繁为简

在小学数学解题中，学生有时会遇到一些关系隐晦、复杂生疏、难以解决的数学问题。此时，教师可以引导学生进行观察、分析、联想、类比，巧借转化思想，将不熟悉、不规范、复杂、抽象的问题转化为熟悉、规范、简单、具体的问题。这样，往往可以收到意想不到的效果。

解析：该题中A校学生总数和B校学生总数的关系比较隐蔽，此时我们可以把已知条件中“A校学生人数的等于B校学生人数的转化成“A校学生人数与B校学生人数的比是，这样使复杂的问题变得简单起来。由此可以求出，A校学生人数校学生人数

【说明】在运用转化思想解题时，需要注意转化的等价性，注重对所给问题的隐含条件的挖掘，从而使得问题得到迅速、巧妙地解决。

二、注重整体思想，纵观全局，化难为易

在小学数学解题中，当某些问题学生从其每个部分或条件去分析解决存在较大难度时，教师可以引导学生将数学问题中的各个部分或条件看成一个系统或整体，纵观全局，全面分析，进而使问题得以快速、有效的解决。

【例2】小张、小李、小赵三人合修一段高速公路，小张修的路是小李和小赵两人所修的路的，小李修的路是小张和小赵两人所修的路的，小赵共修了1250米。这段高速公路长多少米？

【说明】在运用整体思想解题时，需注意从问题的整体性质出发，把握问题整体结构的特性，从而导出问题局部元素的特性，找到解决问题的突破口。

三、巧用分类思想，各个击破，积零为整

在有些数学问题中，由于条件与问题之间的联系是多向的，存在多种情况。此时为了便于有效求解，需要对各种出现的情况进行合理分类，然后逐一分析讨论，各个击破，最后综合归纳，积零为整，得出最终的答案。

【例3】六份同样的礼物，全部分给四个孩子，使每个孩子至少获得一份礼物的不同分法共有多少种？

解析：由题意可知，每个孩子最少可分到一份礼物，最多不会超过三份礼物，所以此题可根据下列两类方法来分：①一个孩子分得3份，其他孩子各分得1份，共有如表1中4种分法；②两个孩子各分得2份，另外两个孩子各分得1份，共有如表2中6种分法。综合①②可知，使每个孩子至少获得一份礼物的不同分法共有：4+ 6=10（种）。

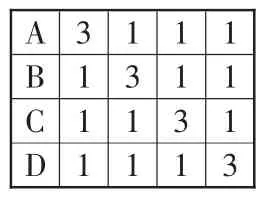
表1　

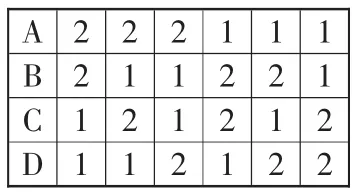
表2　

【说明】巧用分类思想解题，要注意分类的合理性，做到全面统一，不遗漏，不重复，从而提高解题的严密性和完整性，确保解答准确无误。

总之，数学思想方法灵活多样，在平时的数学教学中，教师应从教学实际出发，有效渗透数学思想方法，让学生正确掌握和灵活运用数学思想方法，从而发展学生的数学思维，提升学生的数学解题能力。

（责编黄春香）

G623.5

A

1007-9068（2016）32-088