阳泉市泉西路上跨石太铁路立交桥称重试验分析

杜 光

（山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室，山西 太原 030006）

当新建桥梁跨越繁忙的交通线路既有铁路或高速公路时，为了减小桥梁施工对既有线路的影响，常采用转体桥梁施工方法。同时根据桥梁结构施工时转动方向的不同，又可分为平转法、竖转法以及平转与竖转相结合的方法[1]。由于转体桥梁施工方法具有改善施工条件、施工设备少、操作简便等优点，使得转体桥梁施工法在20世纪70年代后在我国得到了广泛应用，其中又以平转法应用最为广泛。本文结合阳泉市泉西路上跨石太铁路立交桥施工，对桥梁转体施工前的称配重进行技术分析及探讨。

1 工程背景

阳泉市泉西路工程为全定向匝道互通式立交，主线起于南大西街，终点处与既有宏成桥顺接，定位为城区的南北新通道。主线泉西路桥梁全长677.8 m，主桥上跨石太铁路上、下行线及阳泉矿正线，采用变高度T型刚构连续梁。桥梁孔跨布置：1-30 m简支箱梁+2×60 m T构刚构+（45+50+45）m预应力混凝土连续箱梁+3-5×25 m钢筋混凝土连续箱梁。道路等级:城市次干道；设计荷载:城-A级，跨铁路（联跨）孔跨荷载考虑1.3倍放大系数。转体结构由转体下盘、转动球铰、转体上转盘、转动牵引系统组成。钢球铰直径3 700 mm，厚度为30 mm，分上下两片，为转动体系的核心部分。

石太铁路线路繁忙，为最大限度减少结构施工对交通运营的影响，本桥采用平面转体的施工方法。即先沿铁路南侧平地搭设满堂支架分段浇筑梁体，待混凝土强度合格拆除支架后，通过转体就位、然后浇筑两端合龙段，最后使全桥贯通。转体段桥梁长55 m+55 m，转体角度85°，转体重量达10 000 t。原设计全梁施工节段划分情况为：0号段（数量1）、1号段（数量 2）、2号段（数量 2）、3号段（数量 2）、4号段（数量2）、5号段（数量2）；由于季节施工工期变更等原因，全梁施工节段重新划分情况为：A号段（数量 1）、B 号段（数量 2）、C号段（数量2）。

2 转体施工不平衡称重试验

2.1 称重试验的目的

水平转体施工中，能否转的动且转动所需的牵引力很小，并且在转动过程中达到结构的安全稳定是桥梁成功转体的前提条件。一个理想的转动体系统必须同时具备以上两个基本条件。这就需要保证转动体系以转轴为中心所产生的刚体不平衡力矩及摩阻系数要尽量小，然而在实际施工中，尤其是当桥梁采取满堂支架分段现浇法施工时，往往很难做到转轴两侧梁体重量完全一致，因此转体结构均存在着不同程度的不平衡力矩，此时为了消除结构不平衡力矩，保证桥梁结构成功转体，需进行结构称重试验，测试转动体部分的不平衡力矩、偏心距、摩阻力矩及摩阻系数[2]。

围绕阳泉市泉西路上跨石太铁路立交桥结构特点，在桥梁转体前进行称配重试验，测试本转动体桥梁的纵桥向不平衡力矩、偏心距、摩阻力矩及摩阻系数，并确定转动结构的配重方案。

2.2 称重试验前的准备工作

a）撤除梁顶所有材料、机具、设备，清除梁体内杂物；

b）检查并确定上转盘撑脚下滑板上无杂物；

c）安放千斤顶、电子位移计；

d）拆除支架、砂箱；

e）观察转体结构是否倾斜以及倾斜方向，确定其状态。

3 称重试验测试方法及分析

当转动梁体支架全部拆除后，整个梁体的平衡可表现为：

a）转动体球铰提供的摩阻力矩（MZ）大于转动体自身不平衡力矩（MG）。此时，转动体系会维持自身平衡，不会发生任何转动。b）转动体球铰提供的摩阻力矩（MZ）小于转动体自身不平衡力矩（MG）。此时，体系会发生绕球铰的刚体转动，直到撑脚着地受力，体系重新建立平衡状态[3]。

3.1 球铰摩阻力矩大于转动体自身不平衡力矩

设转动体重心偏向太原侧，此时在石家庄侧上承台施加顶力P1（见图1）。当顶力P1增大到足以使结构体系发生转动时，此时可得平衡方程式（1）：

图1 石家庄侧施加顶力

在太原侧上承台实施顶力P2（见图2）。当顶力P2增大到足以使结构体系发生转动时，此时可得平衡方程式（2）：

图2 太原侧施加顶力

解方程（1）和（2），可得不平衡力矩及摩阻力矩计算式。

3.2 球铰摩阻力矩小于转动体不平衡力矩

设转动体重心偏向太原侧，此时，由于撑脚着地只能在太原侧上承台实加顶力P2（见图2）。当顶力P2增大到足以使结构体系发生转动时，此时可得平衡方程式（5）：

当千斤顶顶升到位（使球铰发生微小转动）后，使千斤顶回油，设P3为千斤顶回落过程中使球铰再次发生微小转动时的顶力，此时可得平衡方程式（6）：

解方程（5）和（6），可得不平衡力矩和摩阻力矩表达式。

3.3 摩阻系数及偏心距

根据相关理论推导球铰静摩阻系数及转动体偏心距计算式为：

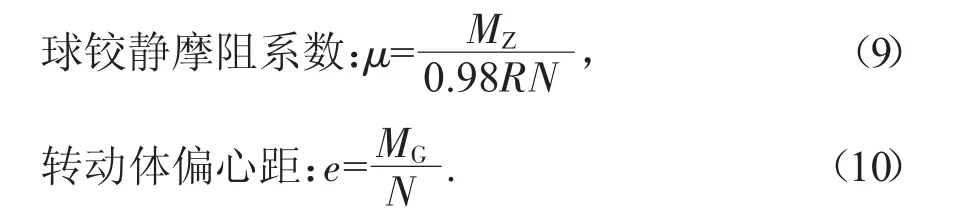
式中：R为球铰转盘球面半径；N为转动梁体重量[4]。

3.4 试验步骤

a）根据梁体脱架后所处形式确定采用何种方式进行称重，在预先拟定好位置处水平安放好压力传感器和位移传感器。

b）调整配套千斤顶和油表到初始位置，注意保持顶升时两台千斤顶顶力同步施加，并做好现场同步记录。

c）千斤顶逐级缓慢加载，保持两侧顶力平衡，避免横向不平衡力矩的产生。

d）密切注视位移传感器的微小变化，直到位移出现较大突变为止；现场整理试验数据，用笔记本电脑同步汇制荷载-位移变化曲线。

e）根据试验测试数据代入以上计算公式，从而得到偏心距、摩阻系数和不平衡力矩。

f）通过测试结果，对转体结构提出配重方案。

3.5 试验所用仪器设备

a）400 t油压千斤顶两台，用于施加顶力。

b）应变式位移传感器6支，用于测试球铰微小转动所产生的结构竖向位移。

c）压力传感器两台，主要技术指标：量程5000kN，测试精度1 kN。

d）智能综合测试仪一台，用于采集压力传感器读数，测试精度1 kN。

e）数据采集系统，采用日本生产的TDS-530数据采集系统，用于采集应变式位移传感器的信号。

f）笔记本电脑一台，用于现场数据处理。

4 试验结果分析及配重方案

4.1 称重试验结果

本次试验梁体脱架完成后，发现石家庄侧正东方向一处撑脚已与滑道钢板接触，说明此时梁体的平衡处于上面所讲第二种平衡形式。根据该状态的测试方法，在石家庄侧上承台底面布置如图3所示的千斤顶和位移传感器。

图3 设备布置示意图（单位：m）

通过石家庄侧加载情况下的荷载-位移变化曲线可以看出，P=4 700 kN为荷载-位移变化曲线的拐点，由此判断出顶升时的临界力P2=4 700 kN。

在石家庄侧落顶情况下的荷载-位移变化曲线可以看出，P=1 113 kN为荷载-位移变化曲线的拐点，由此判断出落顶时的临界力P3=1 113 kN。

图4 顶升时力与位移关系曲线

图5 落顶时力与位移关系曲线

将表1中计算参数按状态2分别代入计算式（7）～式（10）中，可分别求得不平衡力矩、摩阻力矩、摩阻系数及偏心矩。计算结果见表2。

表1 纵向不平衡力矩、摩阻力矩计算参数

表2 纵向不平衡力矩、摩阻力矩、偏心距及静摩阻系数

4.2 配重方案

本次配重采用质量平衡配重的方法。质量平衡配重方案的思路是转动体系在静力状态下保持自身平衡：即根据称重试验结果，通过在T构非偏心一侧箱梁顶上配置一定质量重物，使配重后新的结构体系重心与球铰竖向重心相重合，这样结构体系所有撑脚均不与滑道钢板接触，从而撑脚也均不参与受力。此时结构体系的配重量计算式为：

所需配重=N·e/（悬臂长度－配重距梁端距离）.

该方案最大的优点是减小了配重所需重物质量，从而也减小了T构转体时所需的千斤顶牵引启动力。此时结构体系重心正好落在球铰上，可近似看作单点支撑，因此在转动过程中如遇大风等恶劣天气或外力不平衡状态时，较易出现梁体的晃动。因此，在转动过程中尽量减小了撑脚与滑道的间隙。按该方案转体梁的配重计算结果见表3。

表3 梁体平衡配重方案

5 结论

本次桥梁称重试验过程中，力与位移关系变化曲线拐点明显，临界力确定准确，为大桥准确配重成功转体提供了理论和技术支撑，通过75 min的匀速转动，阳泉市泉西路上跨石太铁路立交桥顺利到达即定位置，成功跨越石太铁路线与两端现浇梁平稳对接，为今后同类转体桥梁工程施工积累了实践经验。