考虑障碍的无线传感器网络连通性恢复策略

马桂真, 于 平

(1.北京联合大学 北京市信息服务工程重点实验室,北京 100106；2.北京邮电大学 网络与交换技术国家重点实验室,北京 100876)



考虑障碍的无线传感器网络连通性恢复策略

马桂真1，2, 于 平1

(1.北京联合大学 北京市信息服务工程重点实验室,北京 100106；2.北京邮电大学 网络与交换技术国家重点实验室,北京 100876)

布置在战场、搜救现场的无线传感器网络往往会遭受大面积破坏，从而将无线传感器网络分割成多个不连通的分区，对网络性能造成很大影响。在这种人工很难干预的场景，无线传感器网络的自主恢复非常重要。提出一种考虑障碍的无线传感器网络连通性恢复策略(OCRS)，利用可移动的无线传感器节点(MDCs)在分区之间移动(收集网络数据)形成暂时的连通线路，在节点移动过程中，考虑路径上障碍。首先构建分区的基于障碍避免的最小生成树，然后优化移动节点的移动路径，最小化移动节点的最大移动距离和总的移动距离。仿真实验结果证实了OCRS的有效性。

无线传感器网络; 连通性恢复； 障碍

0 引 言

在许多应用中，无线传感器网络都布置在条件艰苦、无人值守的环境，比如战场、生命搜救现场等。在这些场景中，无线传感器网络极易受到大面积破坏，使得网络被分割成多个不连通的分区。不同分区之间的节点无法协作，会大大影响无线传感器网络的性能，甚至无法完成任务。在这种情况下，无线传感器网络连通性的恢复就非常重要。

移动无线传感器网络连通性恢复问题研究成为近年来研究的热点7〗。文献中关于无线传感器网络分区连通性恢复方法的研究主要分为三种：一种是在分区之间布置静止中继节点，形成连通网络，这种方法一般是在额外节点充足的情况下进行；一种是在可获得额外节点个数小于分区个数的情况下，利用移动节点收集、交换分区之间数据；最后一种是采用静止和移动节点结合的方法，当可获得的额外节点个数小于形成稳固网络拓扑需要的节点个数，又大于分区个数的时候，一部分额外节点保持静止布置在分区之间，一部分作为移动数据收集者(MDCs)，在分区之间形成暂时的连通链路，进行数据交换。在战场等紧急场景中，网络遭受大面积破坏时，一时很难获得足够多的节点恢复网络的连通性，利用移动节点构建暂时连通网络成为一种解决办法。本文研究移动节点在分区之间移动形成暂时的连通链路，恢复网络的连通性。

利用移动节点构建暂时连通网络成为近年来研究热点，典型的方法有IDM-kMDC],MINDS]和FeSMoR\〗，这几种方法都是利用MDCs在分区之间建立暂时的链路，进行分区之间数据交换，但是所有这些方法都假设节点沿直线移动，路线上不存在障碍，这是不现实的。本文提出一种考虑障碍的无线传感器网络连通性恢复策略(obstacle-aware connectivity restoratio strategy,OCRS)研究障碍情况下，无线传感器网络分区连通性恢复问题，并通过仿真实验验证算法的有效性。

1 系统模型与假设

问题可建模为求无向图的连通性问题。无向图G=(S,E,o)， 其中，S={s1,s2,s3…sn} 代表传感器网络分区集合，E={(si,sj)|si,sj∈S} ，o2={o1,o2,o3,…,om},代表障碍多边形。Dis(si,sj) 表示分区si,sj之间的距离，R表示节点的最大通信范围。为了简单起见，网络中每个分区用一个节点表示，假设网络中至少存在一个障碍，障碍多边形是凸多边形。OCRS首先构建分区最小生成树，在最小生成树构建过程中考虑障碍，然后通过在最小生成树的边放置静态或动态节点，恢复网络连通性，考虑的性能指标是移动节点的最大移动距离和总移动距离。本文还有如下的假设和定义:

假设1：所有的中继节点(用来恢复网络连通性的额外的节点)都可以按需移动。

假设2：网络中至少有一个障碍，每个障碍是一个凸多边形。障碍与网络分区不重合，且最小生成树中至少一条分穿过障碍多边形。

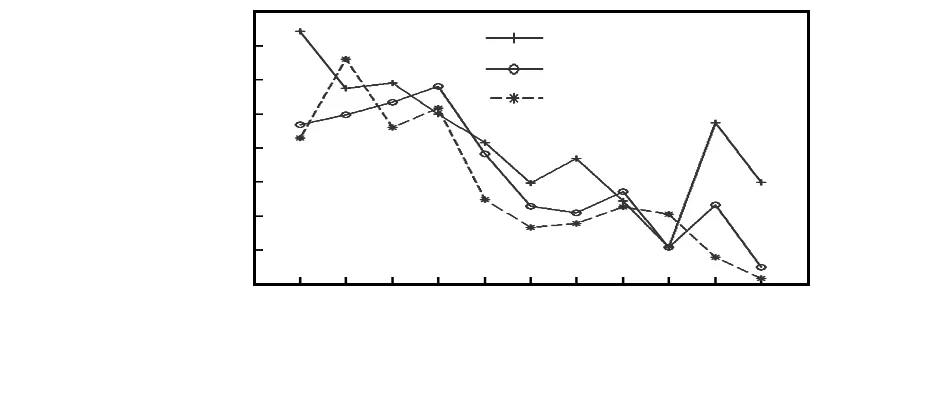
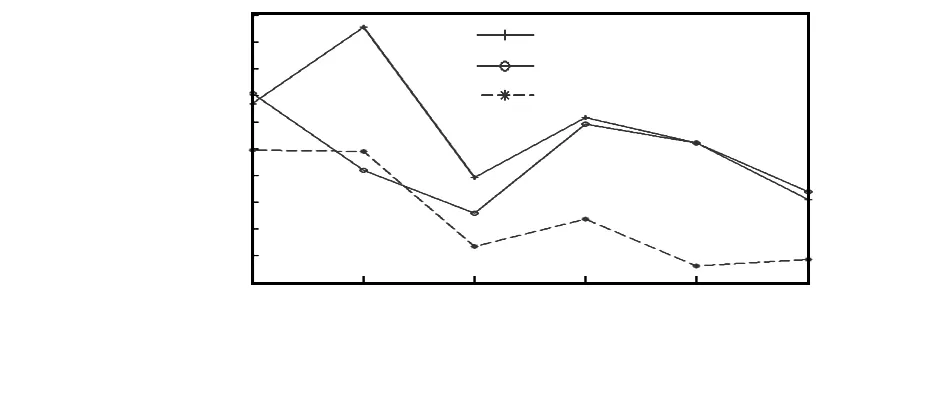
定义2：若M表示分区个数，Navailable表示可获得的中继节点个数，则满足如下表达式Navailable>M且Navailable

2 构建考虑障碍的最小生成树

本文将移动节点总的移动距离(total move length)和最大移动距离(maximum move length)作为算法性能指标，为了尽可能减少节点的总移动距离和最大移动距离，在分区之间构建最小生成树，然后决定在最小生成树的各边布置静止或移动节点。OCRS首先利用Prim算法构建分区之间的最小生成树，然后检测生成树中哪条边穿过障碍，如果边si-sj穿过障碍多边形，则改变该边的线路，绕开障碍。如果有多条边穿过障碍，则分别改变各边的移动路径，改变路径后如果图中不产生环，则算法完成;如果产生环，则将最长边去除，去除图中的环。

如图1(a)，边s2-s7穿过障碍多边形(o1,o2,o3,o4),则比较两条链路s2-o1-o4-s7和s2-o2-o3-s7的长度，选取较短的链路s2-o1-o4-s7代替边s2-s8。而图1(b)中，s2-s7和s2-s8两条边同时穿过障碍多边形，按照图1(a)中算法，分别选取较短的链代替最小生成树中的两条边，树中没有生成环，则算法结束。而对于图1(c)中，s2-s7和s3-s8两条边同时穿过障碍多边形，利用图1(a)中算法分别选取最短的链代替原来的边，这时候，图中产生了环s2-s3-o1-s2,这在最小生成树中是不允许的，OCRS将环中的最长边s2-s3去掉，形成考虑障碍的最小生成树。

图1 考虑障碍的最小生成树构建Fig 1 Construction of obstacle-aware the minimum spanning tree

3 恢复网络连通性

恢复网络连通性的主要工作是在不连通的网络分区之间构建连通链路，即如何布置静止或移动节点在分区之间建立稳固或暂时的连通链路。本文研究的是在中继节点个数不充分的情况下，如何构建连通链路。算法步骤如下：

1)确定中继节点个数

假设最小生成树中所有边都放置静止中继节点，确定需要的中继节点个数Ntotal。如图2，如果最小生成树全部放置静止节点，需要21个静止中继节点，才能恢复网络的连通性。

2)处理沿障碍多边形的边链

由于在障碍多边形边沿放置的无线传感器节点可能受到障碍干扰而影响传输性能，故单独处理边链。在边链上每个障碍多边形顶点各放置一个静止节点，若二个顶点oi,oj之间的距离满足dis(oi,oj)>2R，则放置一个移动节点；若R

图2 形成稳定网络需要的静止中继节点个数Fig 2 Number of static relay node needed for formation of stable network

3)相临边构建三角形

OCRS旨在减少移动节点总的移动距离和最大移动距离，某些相邻的三个节点构成的三角形周长可能比某些边边长要短，为了节省节点移动距离，在节点放置迭代算法开始之前，首先对最小生成树的相临边构造三角形(沿障碍多边形的边链不参与构建三角形)。如图2(b)所示，相临边s3-s4和s4-s5构成一个三角形。而o4-s7是边链，所以,不与边s7-s6构成三角形。

4)具体节点放置迭代算法

Tri表示三角形集合，Et代表最小生成树中边的集合。

若放置的额外节点个数大于Navailable，则执行如下步骤：

a.选择最小生成树中的最短边si-sj，检查三角形集合Tri中是否存在周长小于该边边长的三角形，若存在，则执行(i)，否则,执行(ii)。

(i)若不存在周长小于si-sj边长的三角形，检查边si-sj需要静止节点的个数。如果需要1个静止中继节点即可恢复两个顶点分区之间的连通性，则放置一个静止节点；若需要2个以上的静止中继节点才能恢复顶点分区之间连通性(假设需要N个，N≥2)，则二顶点之间只需放置一个移动节点，这样就可节省N-1个节点。将该边从集合Et中去除。如图3中边s9-s10，只需一个静止节点即可连通s9和s10两个分区，则只需在合适位置放一个静止节点即可。对于边s8-s9，需要两个静止节点才能形成稳固的连通网络，则用一个移动节点代替原来的静止节点，该移动节点在两分区之间移动形成短暂连通线路，这样会节省一个额外节点。

(ii)若存在周长小于边长的三角形，则三角形的三条边上放置一个移动节点，在三个分区之间形成短暂连通线路。如图3中,三角形s3-s4-s5周长小于当前树中最短边s1-s2，则三角形的三条边放置一个移动节点即可。

图3 节点放置完成后的网络拓朴Fig 3 Network topology after finishing node placement

b.对于需要处理的最后一个最短边，比如图3中边s1-s2，若Navailable=18，即只需边s1-s2节省1个节点即可完成网络连通性恢复，在这种情况下，边s1-s2上放置两个静止节点，一个移动节点。这样其余没处理的边全部放置静止中继节点即可。算法结束。

4 仿真实验

在1 200m×1 200m的正方形区域，随机生成网络分区和障碍多边形。实验中，设置传感器网络分区个数从3～13，节点个数变化时，通信范围固定在100m；通信范围变化时，分区个数保持在9个。可获得额外节点个数设置为Navailable=Ntotal×p，其中,0

图4 分区个数变化时最大移动距离Fig 4 Maximum moving distance vs number of segments

图5 分区个数变化时总移动距离Fig 5 Total moving distance vs number of segments

图6 通信范围变化时最大移动距离Fig 6 The maximum moving distance vs communication range

图7 通信范围变化时总移动距离Fig 7 Total moving distance vs communication range

实验结果表明:随着分区个数的增大，节点最大移动距离整体呈下降趋势，总移动距离整体持平；随着节点通信范围的增大，最大移动距离和总移动距离整体呈下降趋势，和实验预期吻合。由于文献中相关方法都没有考虑节点移动过程中遇到障碍的可能性，所以,本实验数据与已有方法实验数据没有可比性。通过优化恢复算法，实验发现在分区个数大于6时,OCRS的性能优于IDM-kMDC，这里由于篇幅限制，不再赘述。

5 结 论

本文提出一种考虑障碍的无线传感器网络连通性恢复策略，利用节点的移动性在网络分区之间形成暂时连通链路。该策略首先构建分区之间的最小生成树，最小生成树的边穿过障碍多边形时，选取较短的边链作为最小生成树的边。然后通过迭代算法确定最小生成树的各边中继节点的放置，完成分区之间连通性的恢复。在后续的研究中，将进一步研究存在多个障碍多边形时，无线传感器网络连通性恢复问题。

[1] Senel F,Younis M.Relay node placement in structurally damaged wireless sensor networks via triangular steiner tree approxima-tion].Computer Communications,2011,34(16):1932-1941.

[2] Akkaya K,Senel F,Thimmapuram A,et al.Distributed recovery from network partitioning in movable sensor/actor networks via controlled mobility].IEEE Transactions on Computers,2010,59(2):258-271.

[3] Younis M,Lee S,Gupta S,et al.A localized self-healing algorithm for networks of moveable sensor nodes]∥2008 IEEE GLOBECOM，2008 Global Telecommunications Conference,IEEE,2008:1-5.

[4] Tamboli N,Younis M.Coverage-aware connectivity restoration in mobile sensor networks].Journal of Network and Computer Applications,2010,33(4):363-374.

[5] Imran M,Younis M,Said A.M,et al.Partitioning detection and connectivity restoration algorithm for wireless sensor and actor networks]∥2010 IEEE/IFIP The 8th International Conference on Embedded and Ubiquitous Computing(EUC),IEEE,2010:200-207.

[6] Senturk I F,Akkaya K,Yilmaz S.Distributed relay node positioning for connectivity restoration in partitioned wireless sensor networks]∥2012 IEEE Symposium on Computers and Communications(ISCC),IEEE,2012:000301-000306.

[7] Stojmenovic I,Simplot-Ryl D,Nayak A.Toward scalable cut vertex and link detection with applications in wireless Ad Hoc networks].Network,IEEE,2011,25(1):44-48.

[8] Senel F,Younis M.Optimized interconnection of disjoint wireless sensor network segments using K mobile data collectors]∥Proc of the IEEE Int’l Conf on Communications,ICC’12,Ottawa,Canada,2012.

[9] Joshi Y K,Younis M.Mobility-based internetworking of disjoint segments]∥2014 The 27th Biennial Symposium on Communications,IEEE,2014:193-197.

[10] Stanislaus J L V M,Younis M.Delay conscious federation of multiple wireless sensor networks segments using mobile relays]∥Proc of the 76th IEEE Vehicular Technology Conference,VTC 2012—Fall,Québec City,Canada,2012.

于 平，通讯作者，E—mail：lytyuping@buu.edu.cn。

Obstacle-aware connectivity restoration strategy for WSNs

MA Gui-zhen1,2, YU Ping1

(1.Beijing Key Laboratory of Information Service Engineering,Beijing Union University,Beijing 100106,China;2.State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China)

Wireless sensor networks(WSNs) in battle field,search and rescue scene are at increased risk of large scale damages and networks are partitioned into disjoint segments.Self-restoring of WSNs in such a case is crucial.Present an obstacle-aware connectivity restoration strategy(OCRS),which places mobile nodes acting as mobile data collectors(MDCs) among segments to provide intermittent communication links.During MDCs traveling,obstacles are taken into account.Construct obstacle-avoiding minimum spanning tree of segments,and optimize mobile node travel routers.Minimize the maximum moving distance and total moving distance of moving node.Effectiveness of OCRS is validated through simulation experiments.

wireless sensor networks(WSNs); connectivity restoration; obstacle

2015—11—13

10.13873/J.1000—9787(2016)10—0123—04

TP 212.9; TN 929.5

A

1000—9787(2016)10—0123—04

马桂真(1979-)，女，山东单县人，博士研究生，讲师，主要研究方向为无线传感器网络故障管理。