城市道路交通标志牌基础设计研究

张志伟，任 强

（青岛市市政工程设计研究院有限责任公司，山东 青岛 266000）

城市道路交通标志牌基础设计研究

张志伟，任 强

（青岛市市政工程设计研究院有限责任公司，山东 青岛 266000）

为解决城市道路交通标志牌基础与市政管线之间的冲突，合理确定标志牌基础尺寸。首先采用有限元软件对标志牌振动模态进行分析求得其自振周期，确定是否考虑顺风向风振的影响；再依据新版《建筑结构荷载规范》（GB 50009—2012）进行风荷载计算，并在一定的约束条件下对基础的尺寸进行分析，合理确定基础尺寸的大小；最后，结合实际工程对标志牌基础与市政管线之间的冲突问题提出了解决方案。

交通标志牌；振动模态；风荷载计算；基础尺寸

0　引言

在市政道路的建设过程中，道路交通标志牌的设置是必不可少的一环。对于沿海地区，一些大型交通标志牌受到的风荷载较大。为满足结构安全要求，基础所需要的混凝土的体量是很可观的，但由于市政道路与公路不同，地下敷设相当丰富的管线，特别是靠近路缘石附近，是地下管线争夺的焦点。标志牌基础一般也正好设置于这一位置，因此与地下管线线位发生冲突在所难免，特别是一些大型标志牌，由于基础尺寸较大，这一问题变得更加明显。

针对上述问题，本文依据新版《建筑结构荷载规范》（GB50009-2012）［1］，对沿海地区某一大型标志牌进行风荷载计算，进而对标志牌所需基础尺寸进行合理分析，以尽量减少基础与管线线位的冲突，并提出一些在设计及施工中应注意的问题。

1　计算及分析过程

1.1工程背景

青岛沿海某一主干路，道路沿线交通标志牌面板尺寸采用3 m×6 m，其结构如图1所示。支承杆件采用3F杆，杆件与基础之间采用高强度螺栓进行连接，基础尺寸暂定为a（宽）×l（长）×h（高），立杆、横梁及面板材料见表1。道路沿线敷设有给水、排水、电力、通信、燃气等管线，部分管线线位与标志牌基础存在冲突。

1.2荷载分析及假定

标志牌上的作用力可分为永久作用和可变作用两类［1］。永久作用主要包括杆件自重、标志牌或固定设备自重、土压力和地基变形等；可变作用包括风荷载、覆冰荷载、雪荷载、安装或检修荷载、地震荷载、温度荷载等。其中，风荷载是结构承受的主要荷载。本文也着重研究风荷载对标志牌的作用，并在计算分析的过程中作如下的假定：

（1）假定风荷载方向与标志版面垂直，不计扭转或位移对风荷载的影响；

（2）基础四周土的摩擦力和抗力忽略不计，作为安全储备；

（3）忽略横风向风振和扭转风振的影响。

图1　交通标志牌示意图（单位：cm）

1.3标志牌振动模态分析

如前所述，本文主要考虑风荷载对标志牌的作用。影响风荷载大小的因素有基本风压、风荷载体型系数、风压高度变化系数、风振系数。前面三项可由规范直接取值［1］，而风振系数的计算需要计算结构的自振周期，然而在新版的《建筑结构荷载规范》（GB50009-2012）以及《户外广告设施钢结构技术规程》（CECS148-2003）［2］中对结构的自振周期均要求采用结构动力学计算或采用近似计算，但是并未给出此类构件的近似计算公式。因此，有必要对标志牌的振动模态进行分析，从而求得与风振系数有关的自振频率、自振周期以及振型系数等参数。

结构振动模态的分析可借助于通用有限元软件，比如ANSYS、SAP2000、MIDAS来实现［3，4］。本文即采用有限元分析软件MIDAS/Civil进行结构的离散和模型的建立，将标志牌划分为59个梁单元和48个板单元，立杆底部采用固结处理。具体的建模参数见表1。表2和图2分别给出了前四阶振动模态的示意图和计算结果。其中，一阶模态自振频率f=1.215 Hz，自振周期为T=0.823 s，振型系数为0.99。根据规范要求，自振周期大于0.25 s，需要考虑风压脉动对结构顺风向风振的影响［1］。

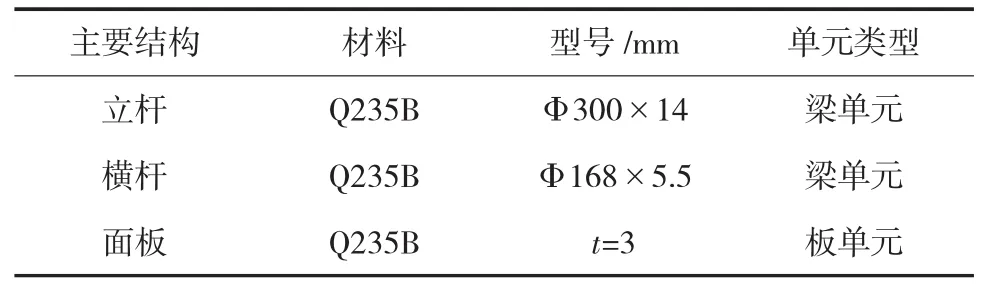
表1　建模参数

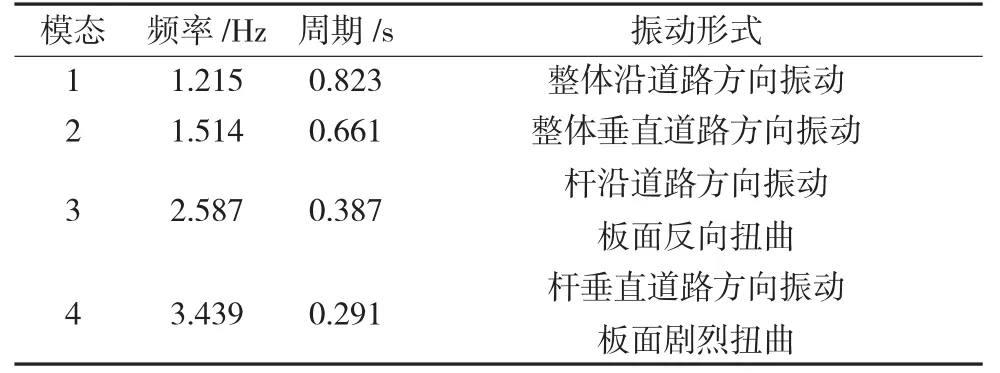
表2　各阶模态自振频率及振动形式

1.4风荷载计算

标志牌风荷载计算依据新版《建筑结构荷载规范》（GB 50009—2012）中8.1.1条计算：

式中：βz为高度z处的风振系数；μs为风荷载体型系数，取1.3；μz为风压高度变化系数，沿海地区，地面粗糙度为A类，查表取1.28；w0为基本风压（kN/m），取青岛本地50 a一遇基本风压w0=0.6 kN/m2。

对于风振系数的计算，新版《建筑结构荷载规范》与旧版比较，变化较大，现依据新版规范进行计算。对于一般竖向悬臂型结构，可仅考虑结构第一振型的影响［1］，根据规范8.4.3条：

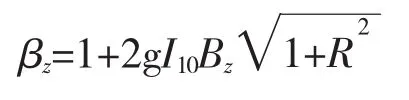
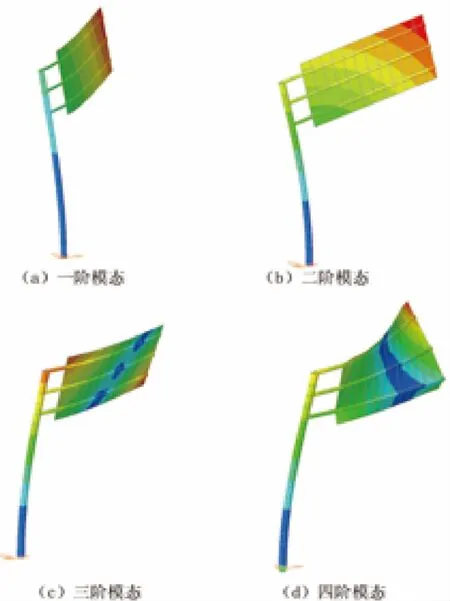
图2　一阶至四阶模态示意图

式中：g为峰值因子，可取2.5；I10为10 m高度名义湍流强度，对A类地面粗糙度，可取0.12；R为脉动风荷载的共振分量因子；Bz为脉动风荷载的背景分量因子。

公式中R与Bz计算过程较为繁琐，限于篇幅，不再一一赘述。这里仅给出计算结果，见表3。表3公式中的参数的具体含义见《建筑结构荷载规范》（GB 50009—2012）。

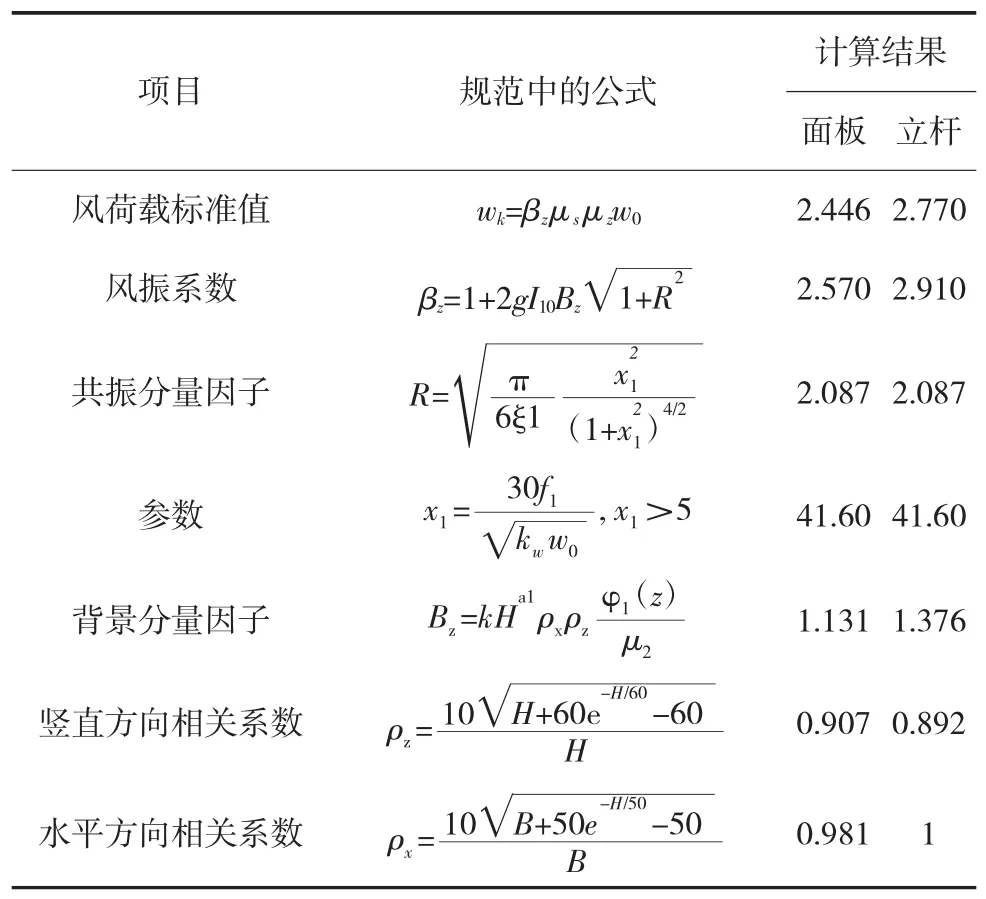
表3　风荷载标准值计算结果

1.5基础尺寸的分析

按照上述步骤求出风荷载标准值以后，即可计算基础底面的倾覆力矩，一般情况下，确定基础尺寸需要满足的条件主要有：

（1）抗倾覆稳定系数不小于1.3；

（2）基础底面零应力区不大于底面积的25%；

（3）满足地基承载力要求。

从理论上说，基础尺寸可以有无数种组合，若给其加上一系列的约束条件，并提出一个明确的目标函数，这样就可以建立相应的数学模型，采用下面优化原理来进行求解。

优化的数学模型主要包括设计变量、目标函数和约束条件三方面。设计变量是指在优化过程中所要选择的基本参数，对于本文要研究的内容来说，设计变量是标志牌的基础尺寸：a、l、h；目标函数是衡量优化方案的标准，本文的目标函数可采用基础混凝土最小用量来表示，即min｛a×l×h｝；约束条件是在优化的过程中所要考虑的种种限制，对于本文来说，包括基础尺寸的合理范围以及上面所需要满足的三个条件等。具体的数学模型描述如下。

设计变量：基础的尺寸a、l、h

目标函数：min f（a、l、c）=a×l×c

约束条件：a1＜a＜a2

l1＜l＜l2

h1＜h＜h2

K＞1.2

P＜25%

式中：a、l、h为基础尺寸；a1、a2、l1、l2、h1、h2为基础尺寸的合理范围；K为基础抗倾覆稳定系数；P为基础底面零应力区占底面积的比值。

上述数学模型是一个典型的非线性优化问题，可采用通用软件Matlab中的fmincon函数进行优化计算［5］，这样就会得到唯一的最优解。

但是对于实际工程来说，基础尺寸不需要很精确的数值，可以编制相应的计算表格进行计算。通过对基础尺寸进行分析，得出如下规律：

（1）抗倾覆稳定性较容易满足，基础底面零应力区不大于底面积的25%成为主要的制约条件。

（2）基础沿风荷载方向尺寸越大，相同条件下所用混凝土体量越小。

（3）基础平面尺寸越大，相同条件下基础底面零应力区不大于底面积的25%，这一制约条件更容易满足，而增加基础的高度并不明显。

2　解决方案

通过上述分析可知，标志牌基础的尺寸可以在一定的范围内进行调整，结合施工中标志牌基础与管线线位冲突这一实际问题，可采用以下解决方案：

（1）标志牌基础尽量与地下管线工程同步实施，实施过程中可以通过调整基础的位置、尺寸或管线局部的线位进行相互避让；

（2）若标志牌基础施工时遇到已实施的管线，也可通过调整基础的位置或尺寸避让现状管线，必要时可做成不规则的基础形状。

针对该工程而言，由于管线影响，部分标志牌基础宽度限制在1～1.5 m，据此拟定了一些常规的尺寸给实施单位选择使用，见表4。

表4　部分基础尺寸示例

从表4可以看出，在满足抗倾覆稳定要求及基础底面零应力区要求的基础上，混凝土体量的变化还是较大的。因此，若能采取合理的尺寸，可以从一定程度上减少混凝土的用量。从表4中还可以看出，基础抗倾覆稳定系数较大，若能放宽基础底面零应力区所占底面积比例这一条件，基础尺寸尚能进一步减小。

另外，若在基础实施的过程中实在无法与管线避让，可在保证管线安全的前提下，将管线与基础浇筑成整体，必要时采用桩基础形式。

3　结　语

道路标志牌的自振周期一般较长，计算风荷载时风压脉动对结构顺风向风振的影响不能忽视。在拟定标志杆基础尺寸时，可以有多种不同的组合，应根据工程的不同的约束条件确定合理的尺寸，一方面可以有效解决与管线线位冲突这一问题，另外一方面可以减少混凝土用量，降低投资。

在实际的设计过程中，还应对标志牌杆件结构及高强度螺栓连接按照《钢结构设计规范》（GB 50017—2003）进行设计或校核。混凝土基础则还应依据《混凝土结构设计规范》（GB 50010—2010）进行结构计算，并配置相应的受力钢筋及构造钢筋，尤其对于非常规基础，配筋应予加强。

另外，在对横风向风振系数进行分析时，新规范中一些参数的计算是基于房屋等建筑结构类型，对于道路标志牌这种构件类型的适用性还有待进一步研究。

［1］GB 50009-2012，建筑结构荷载规范［S］.

［2］CECS148-2003，户外广告设施钢结构技术规程［S］.

［3］刘成生，郭成喜，高金锁.某钢结构广告牌结构分析［J］.工业建筑，2010（40）：553-555.

［4］张传斌，杨邦成，姚激.标志牌杆在风荷载作用下的有限元［J］.特种结构，2011（2）：22-24.

［5］杨世文，许小健.MATLAB优化工具箱在结构优化设计中的应用［J］.科学技术与工程，2008（5）：1347-1349.

U491.5+2

A

1009-7716（2016）01-0022-03

10.16799/j.cnki.csdqyfh.2016.01.008

2015-02-13

张志伟（1983-），男，山东德州人，工程师，从事道桥设计工作。