高等数学课程嵌入数学实验的研究
刘程熙 马常友
高等数学课程嵌入数学实验的研究
刘程熙马常友
(内江师范学院,四川 内江 641112)
在高等数学课程教学中开展数学实验的模式进行了研究,给出了一元微分部分实验的框架图,并列举了两个探究性实验的实例。
高等数学;实验;实验框架
0 引 言
高等数学课程以微积分为主要内容,其得益于物理学和天文学的发展,是理工科学生的专业必修课程,主要授课对象为大一的新生。由于高等数学内容的抽象性,导致大多学生感觉学习困难,而容易放弃学习。这个现象已经引起了众多教育工作者的反思[1-7]。实际上,理工科学生学习高等数学知识为后继课程的学习奠定基础,然而,大一的新生对自己专业所需的知识不甚了解,高等数学的学习让学生觉得是从数学到数学的脱离生活实际的高雅科学,对为什么要学习高等数学感到迷茫。文献[8]指出:“数学有两个侧面,一方面是欧几里得式的严谨科学,但另一方面是创造过程中的数学,看起来却像是一门实验性的归纳科学”。让学生体会到数学来源于生活,并可返回解决实际问题,不但可提高学生的学习兴趣,还可培养学生的创新能力。一种行之有效的方法即是将数学实验嵌入到高等数学教学中。本文将从模式介绍、设计框架、和探究型实验举例这三个方面进行讨论。
1 数学软件及实验模式介绍
由于高等数学的面向对象是大一的新生,其计算机编程能力有限,因而在大一的上期数学实验样以简单的操作为主。
在数学软件的选取上,由于Matlab软件可以进行代数运算、求极限、求微商、求积分、解微分方程,并且可以作图,满足大一上期学生学习的需要,因此我们选择的是Matlab软件。
我们采取的模式不是到了一学期期末才给学生介绍几个学时的数学软件,让学生练习,这样会让学生觉得实验和高等数学课程是两个平行的个体,相互独立,我们采用的方式是将数学实验内容分散化,嵌入到高等数学理论知识的学习中,实践证明这样可帮助学生理解高等数学的相关知识。
2 一元微分部分实验框架设计
在大一上期,我们开设了两种类型的实验,一种是验证性实验,一种是探究性实验。验证性实验的开设主要针对求极限、求导数、求定积分,在这个环节主要是介绍输入命令相应格式,并且进行演示,让学生根据介绍自己去验证理论求出来的结果和计算机得到的结果是否一致。而探究性实验主要是教会学生描绘一次函数的图形,针对大一的学生通过授课我们发现,学生一遇到问题很容易想到利用作图来进行说明,虽然作图不能代替证明,不具有严格的逻辑性,但是作图缺可以帮助学生理解。因此我们做了三个实验一个是作出的图像,观察当曲线的走势,估计极限;第二个是在学习了泰勒展式之后,在同一个图中,画出不同的多项式对应的图形和已知函数的图像进行对比,观察接近程度;第三个进行图像的描绘探索绘图的步骤及绘图增加的点的情况。下面以一元微积分部分实验给出框架构造图。
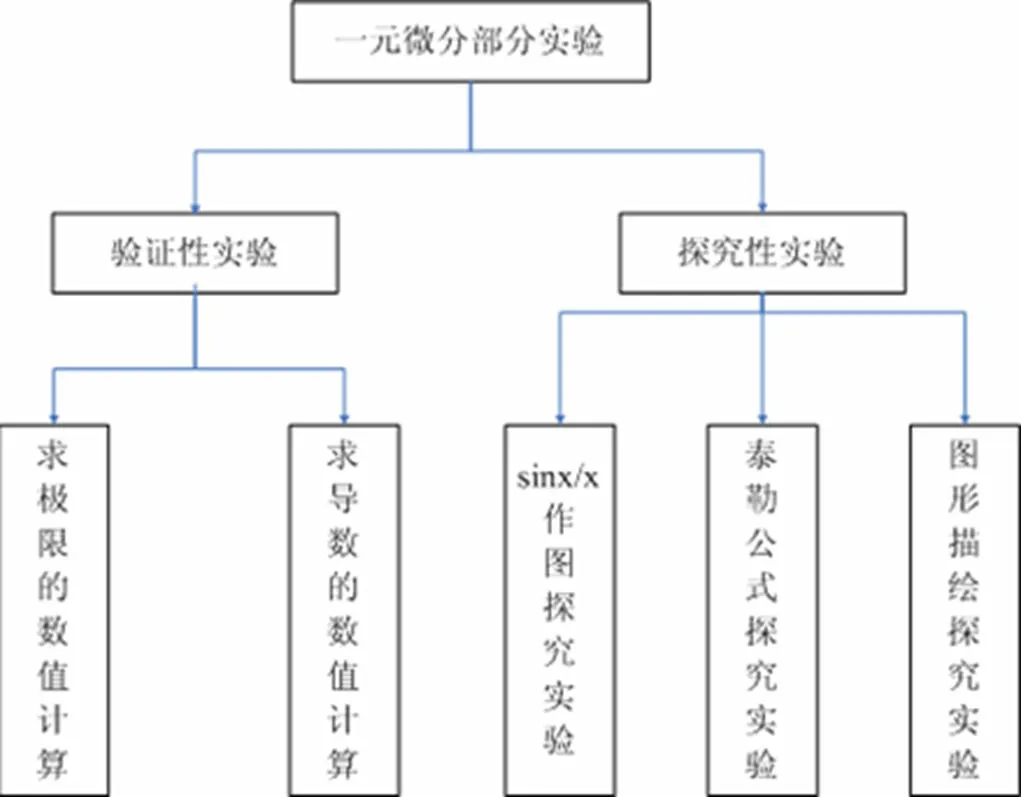
图1.一元微积分部分实验框架图
3 探究性实验举例
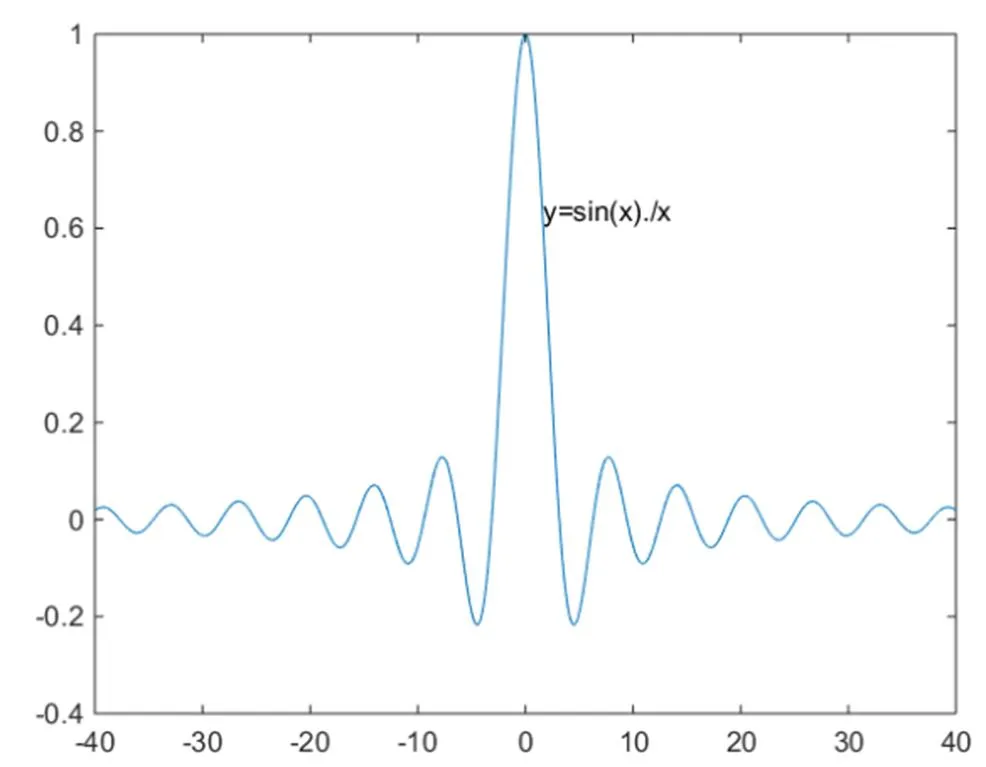
图2.函数在[-40,40]之间的图像
学生有很强的形象思维能力,同时在中学教师主要教给学生判断极限的方法就是做图观察。利用学生的这种特性,学生很容易观察得到:,这两个易错的极限。同时在这个地方同时介绍作图的简单命令,让学生熟悉,为后面做出其他更多要求的图像做准备。

图3.几个函数图像的对比图
这个实验对学生做图提出的要求更高,但只需在前面的基础上增加几个命令,采用螺旋式上升方式进行作图教学,可以让学生逐步掌握作图的方法,为做出空间图形做出铺垫,同时为了做出图学生会去查阅资料,激发学生的自学能力。通过这个实验能让学生体会研究泰勒公式的必要性。
4 小 结
在大一上期,主要介绍基本的数值计算命令和简单的二维图形绘制。到了大一下期学生有了一定的编程能力,可以编程解决实际问题,达到逐步提高。将数学实验融入到高等数学的教学中,不能忘记数学是一门严谨的科学,不能因为计算机功能的强大,而忽略对学生数学基本素养的培养。实践表明,将数学实验嵌入到高等数学的教学中,改变了一味的老师讲,学生被动学的局面,并能将抽象的知识变得形象生动,与大一新生有很强的形象思维能力的特点相吻合。
[1]张美恋.本科院校工科高等数学软件实验的改革[J].宁德师范学院学报,2015,(1):66-69.
[2]周立平.《高等代数》课程实验教学探究[J].湖南科技学院学报,2010,(4):21-23.
[3]郑宗剑,刘浏,张斌儒.数学建模和数学实验融入高等数学教学改革初探[J].四川文理学院学报,2012,(2):146-149.
[4]陈静.高等数学课程教学改革与实践[J].当代教育理论与实践,2015,(10):95-96.
[5]胡桐春.高等数学教学与数学实验[J].高等教育研究,2006,(2):40-41.
[6]周莉,程雅丽,张敬.高等教育大众化背景下高等数学教学改革[J].理论观察,2015,(6):172-173.
[7]王凡刚.在高等数学教学中开展数学实验的探讨[J].长春大学学报,2011,(10):78-81.
[8]G.波利亚.数学的发现(第二卷)[M].北京:科学出版社, 1987.
(责任编校:何俊华)
2015-11-19
教育部数学与应用数学专业综合改革项目(项目编号ZG0464);四川省数学与应用数学专业综合改革项目(项目编号01249)。
刘程熙(1977-),女,四川大竹人,硕士,副教授,研究方向为偏微分方程的数值。马常友 (1987-),男,四川乐至人,内江师范学院实验师,研究方向为微分方程算法设计。
G642
A
1673-2219(2016)05-0014-02

