钻地弹斜侵彻混凝土靶的工程计算模型
薛建锋, 沈培辉, 王晓鸣
南京理工大学 机械工程学院, 南京 210094
钻地弹斜侵彻混凝土靶的工程计算模型
薛建锋, 沈培辉*, 王晓鸣
南京理工大学 机械工程学院, 南京210094
为了研究侵彻过程中钻地弹受力不对称性下的运动轨迹,结合动力学基本方程和经典空腔膨胀理论,基于层裂机理,建立了具有倾角和攻角相结合的卵形弹侵彻混凝土的工程模型。利用该模型得到了弹体头部运动轨迹与倾角、攻角以及速度的关系,结果表明侵彻深度随着倾角的增大而明显减小,弹体头部运动轨迹的弯曲弧度也越大;攻角越大,产生的偏转力矩越大。对工程模型进行试验验证,结果吻合较好,该模型能够有效地反映出斜侵彻过程的主要特征,进而说明该模型的适用性与合理性。
冲击动力学; 钻地弹; 斜侵彻; 层裂机理; 运动轨迹
钻地弹是一种携带钻地弹头(又称侵彻战斗部)主要用于攻击机场跑道、地面加固目标、 深入地下的指挥中心和工事等目标的信息化弹药,其侵彻作用是对坚固的地下工事实施打击破坏的重要手段,混凝土材料在军事工程上被广泛应用,因此钻地弹侵彻混凝土问题一直受到武器研制和工程防护部门的关注。考虑到目前许多类型的钻地弹都挂载在轰炸机或是装载到导弹之上,钻地弹脱离载体时,其姿态具有一定的任意性。弹体在着靶前有一段自由或者简易控制的飞行过程,在此过程中它又受到重力和空气流等不对称的作用(尽管弹体自身可能携带的控制装置能对其着靶姿态作一定的调整),因此弹体往往不是垂直入射目标,而是与目标外表面法线成一定夹角侵入其内部。
对斜侵彻问题的研究可为钻地弹的设计以及防护工事的构筑提供重要的参考依据,因此国内外学者一直都予以高度重视。Benmard[1]、Roisman[2]和Forrestal[3-4]等对弹体的斜侵彻过程进行了研究,分析问题的侧重点则放在弹体表面附近的速度势、速度场的分析和计算上,阻力计算时又以弹体全表面积分为其分析基础,因此与动能弹斜侵彻混凝土靶的情况有很大的差异。Macek[5]、Longcope[6]和Warren[7]等分别采用折减函数与衰减函数对靶体受力进行研究,并未考虑非对称下弹体头部上下表面的阻力。高世桥[8]、李进忠[9]和尹放林[10]等没有对弹体在开坑阶段的受力及其不对称性进行描述,因此其合理性还有待验证。张刚明等[11]没有考虑弹体的转动对其不同侧面、不同位置点的法向速度的影响。何涛[12]用ABAQUS软件对弹体斜侵彻不同靶板介质进行了大量的数值仿真,但没有考虑自由表面效应对弹道偏转的影响。为了弄清楚斜侵彻机理,国内学者就斜侵彻也进行了大量试验[13-20]。
综上所述,以往文献并没有考虑弹体所受阻力的非对称性,因此本文考虑表面层裂机理,结合刚体运动学理论,将靶板自由表面对弹体侵彻规律的影响引入到斜侵彻混凝土靶的理论计算当中,建立了弹体斜侵彻混凝土靶的计算模型。为了对上述斜侵彻计算模型进行验证,开展了钻地弹斜侵彻混凝土靶的试验研究,获得了靶板典型的破坏模式、弹体的侵彻深度(弹尖与靶面的垂直距离)和最终转角(斜侵彻结束时的弹体转角)等试验数据,从而对理论模型进行了验证。
1 斜侵彻的数学模型
1.1基本假设与坐标系的建立
与众多关于斜侵彻的文献[1,8-9,11]类似,对钻地弹斜侵彻混凝土靶问题进行如下假设:
1) 弹体轴线和靶板外表面法线构成一个平面——弹道平面,该弹道平面固定不动,弹体的速度矢量始终在弹道平面内,且不产生跳弹现象。
2) 弹体不绕其轴线旋转,且以初始攻角斜撞击混凝土靶板,其着角(着靶角)定义为在弹体着靶时,其轴线与靶板外表面的夹角,而称侵彻过程中弹体轴线绕过质心且垂直弹道平面的质心轴转动的角度为转角(偏转角)。
3) 弹体在侵彻过程不发生变形,即保持刚性。
4) 弹体的斜侵彻过程可由刚体的平面运动微分方程加以描述。
根据弹体斜侵彻混凝土靶的过程,建立了卵形弹斜侵彻的坐标系,如图1所示,其中动坐标系为x1o′y1和x2o′y2,定坐标系为x0oy0。
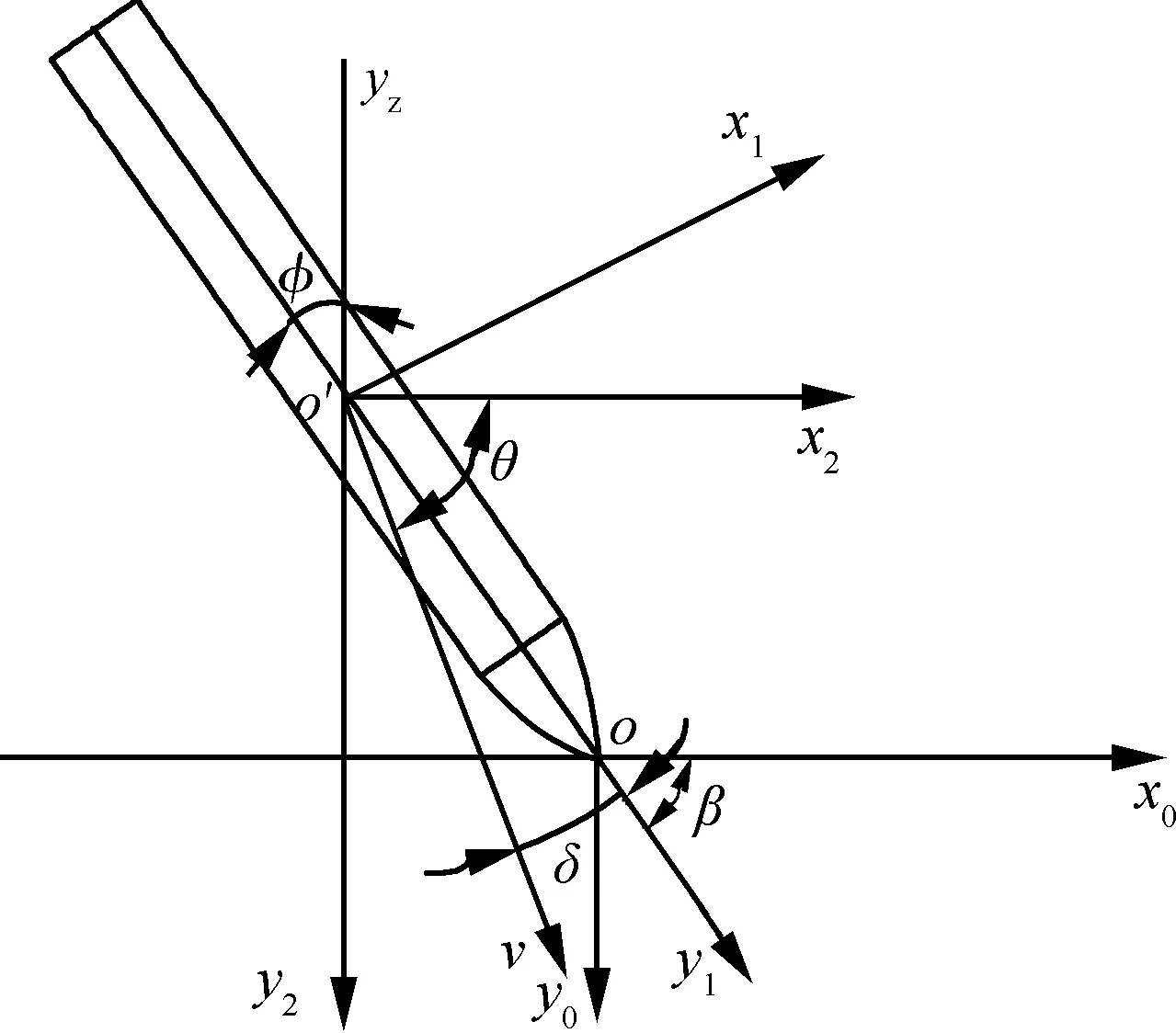
图1 弹体斜侵彻坐标系示意图Fig.1 Sketch map of coordinate system of oblique penetration projectle
1.2弹体运动微分方程
弹体着靶初始姿态如图1所示,着角为β,倾角为φ,攻角为δ,落角为θ,且δ=θ-β。弹体受力情况如图2所示,侵彻阻力沿速度矢量的分力和垂直于速度矢量的分力分别为Fs和Fc,侵彻阻力沿水平方向的合力和沿竖直方向的合力分别为Fx2和Fy2。绕垂直于入射平面的质心轴转动的转动惯量为I0、角加速度为ε,绕垂直于入射平面质心轴的力矩为M0。
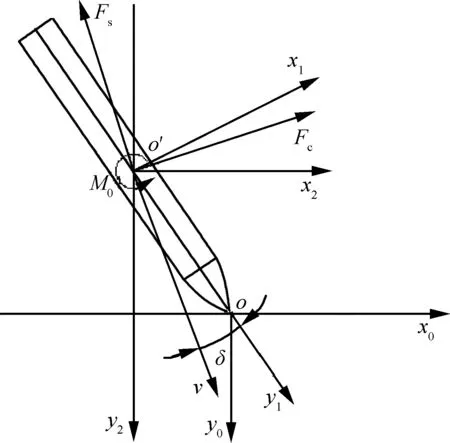
图2 弹体受力图Fig.2 Force diagram of projectile
在x2o′y2坐标系中,弹体质心的运动方程为
(1)
(2)
I0ε=-M0
(3)
弹体质心速度v在坐标系x2o′y2中的轴向分量为
(4)
(5)
对式(4)和式(5)进行微分可得
(6)
(7)
综合式(1)、式(2)和式(6)、式(7)可求得
(8)
(9)
假定弹体绕射平面质心轴的旋转角速度为ω,由弹体质心的速度v可得弹体接触面任一点的法向速度vn和切向速度vτ分别为
(10)
(11)
式中:ω=dβ/dt,顺时针为负;θt为弹体表面某一点法线方向与弹轴的夹角;γ为弹体表面某一点法线方向与射平面(靶体法线与弹体轴线所在平面)的夹角,范围为-90°~90°;“±”表示弹体接触面相对于靶体自由表面而分成的上下表面,当取“+”时,为上接触面,当取“-”时,为弹体头部下表面,如图3所示。
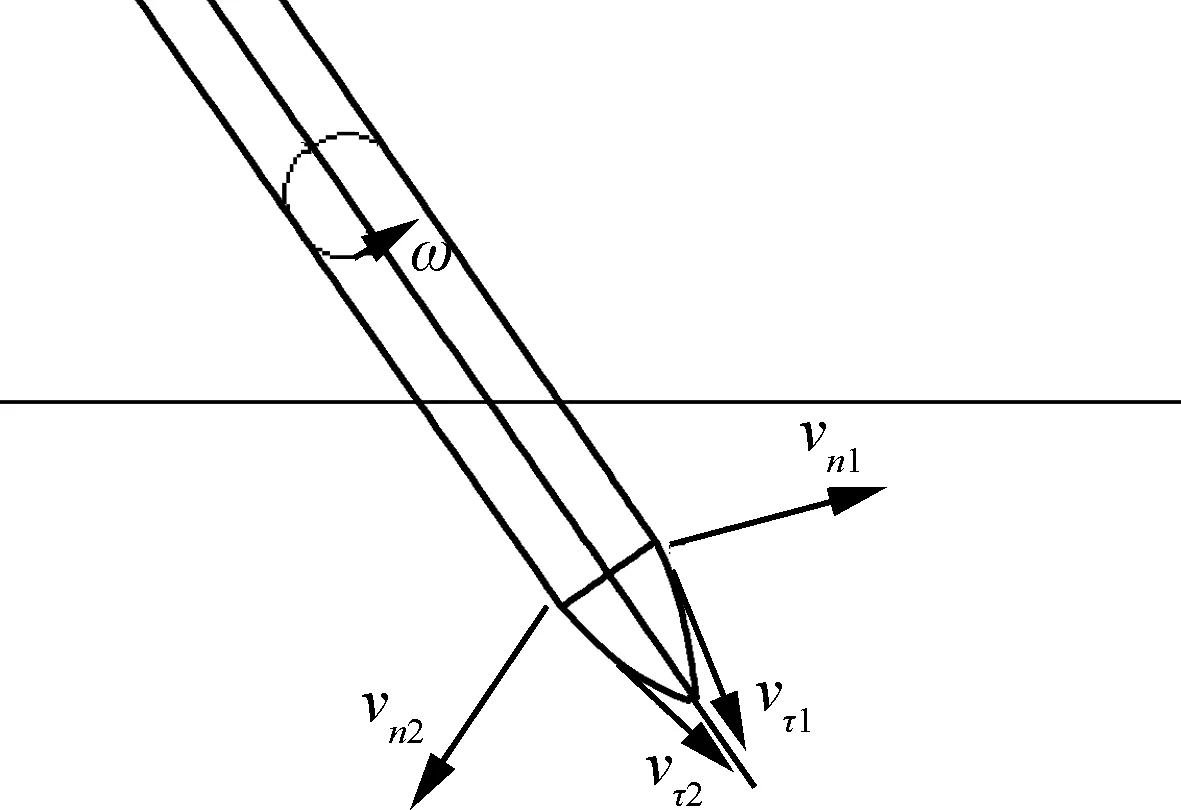
图3 接触面上的速度分布Fig.3 Velocity distribution on contact surface
1.3头部表面法向应力
根据文献[21]的空腔膨胀理论,作用在弹头上的阻力主要包括两部分:强度效应和惯性效应。确定破坏区内径向应力为
(12)
(13)
1.4表面层裂对斜侵彻的影响
弹体斜侵彻混凝土过程中,产生的应力波斜入射自由表面,入射波在自由表面除了反射出膨胀波,还反射出剪切波,并且这2种反射波的强度分配与入射角有关,剪切波对侵彻过程的影响程度小,在此忽略剪切波的影响。
某一时刻压缩波斜入射到自由表面,在自由表面某一位置到达并反射。图4是某时刻在自由表面处压缩波入射和反射的图像,图中MN为自由表面。
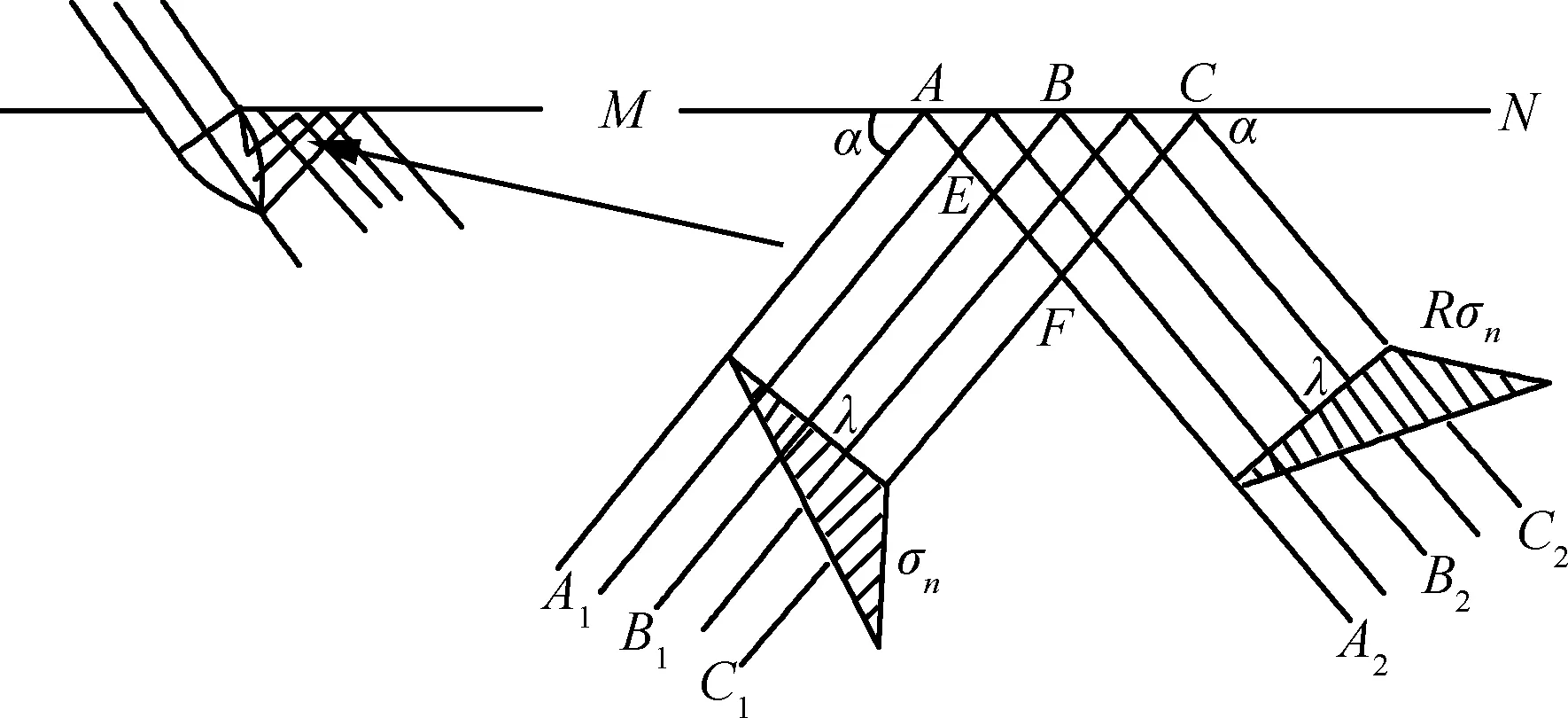
图4 某时刻压缩波在自由表面的反射Fig.4 Reflection of plane wave at free surface at a time
设入射压缩波波长为λ,波头强度为σn,入射角为α,按照反射纵波和入射纵波的关系,可知反射波的波长为λ,反射角为α,反射波波头强度为Rσn,R为反射系数,它是入射角α和材料泊松比ν的函数,表示为[22]
(14)

图5 波的叠加Fig.5 Superposition of waves
图4中E点处应力为反射波波头强度和入射压缩波1/2波长处的强度按相交角度180°-2α进行叠加;F点处应力为反射波波头强度。在反射压缩波与入射波相交线上,任选一点G(见图5),设G距入射波波头阵面的距离为ξ,入射波的强度为σI=(1-ξ/λ)σn,其方向沿入射波波阵面法线方向,G点处反射波强度为σII=Rσn,其方向沿反射波波阵面法线方向,二应力之间的夹角为180°-2α,按照计算纵波叠加主应力公式,可以计算σI、σII叠加后的主应力为
(15)
根据式(15)求得的主应力为拉应力,且最大拉应力大于混凝土的抗拉强度极限,这时在混凝土内部将出现层裂,层裂方向垂直于最大拉应力方向。层裂位置距自由表面的距离为
(16)
1.5侵彻阻力
根据层裂机理和力的分解得到任一微元dA,在侵彻过程中靶体作用在该微元的力有法向阻力dFn和切向阻力dFτ,其分别为
(17)
(18)
式中:μ为摩擦因子。
弹体表面任一点微元上的法向阻力dFn和切向阻力dFτ向x1轴和y1轴投影,得
(19)
(20)
将式(17)和式(18)代入式(19)和式(20),得
(21)
(22)
沿x1轴方向的力垂直于射平面质心轴的力矩为
dMx1=(dFx1)y1
(23)
沿y1轴方向的力垂直于射平面质心轴的力矩为
(24)
式中:R′为弹体表面圆周半径,且
(25)
其中:s为曲率半径;a为弹体半径;ld为弹体头部的长度;L0为弹尖到质心的距离。
弹体的斜侵彻过程分为如图6所示的4个阶段:第1阶段,只有部分弹头部侵入靶体;第2阶段,部分弹头和部分弹杆侵入靶体;第3阶段,弹头部完全侵入靶体,部分弹杆部侵入;第4阶段弹体完全侵入靶体。为了方便计算弹体侵入过程中所受的靶体阻力,将侵入靶体的弹体曲面分别向弹体质心处的横截面投影。
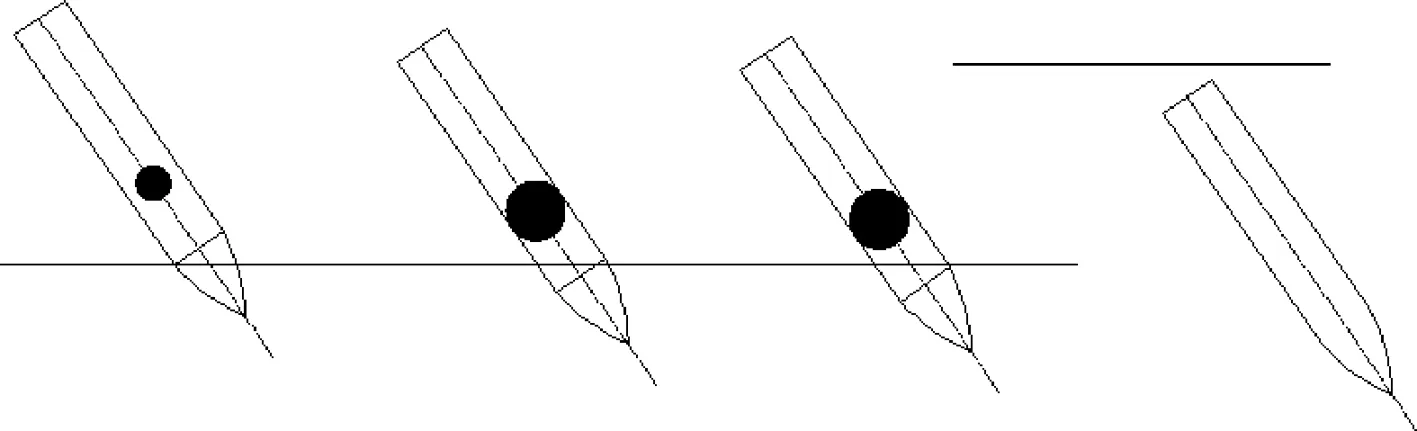
图6 斜侵彻的4个阶段Fig.6 Four stages of oblique penetration
表面微元体在y1轴的坐标可以表示为
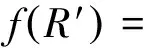
(26)
该微元体的法线方向和弹轴的夹角为
(27)
由图7弹体几何关系可得
(28)
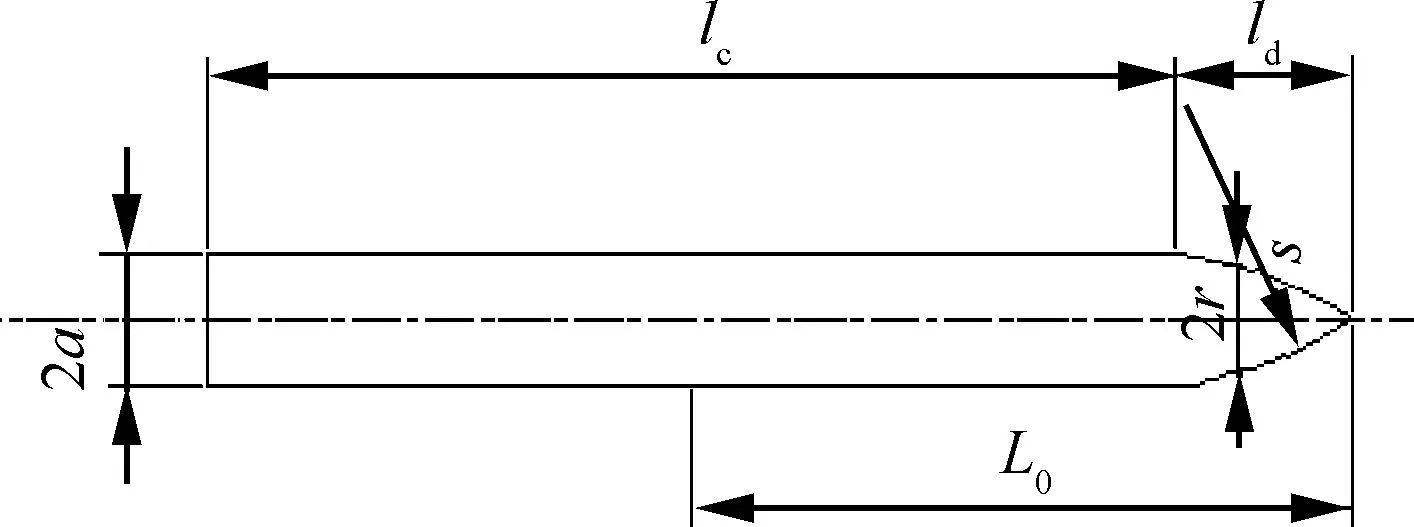
图7 弹体几何形状Fig.7 Geometric shape of projectile
将式(27)和式(28)代入式(10)和式(11),得接触面处靶体任一点的法向速度和切向速度为
(29)
(30)
弹体头部表面微元所受的阻力和阻力矩沿x1轴和y1轴方向的分量分别如下所示。
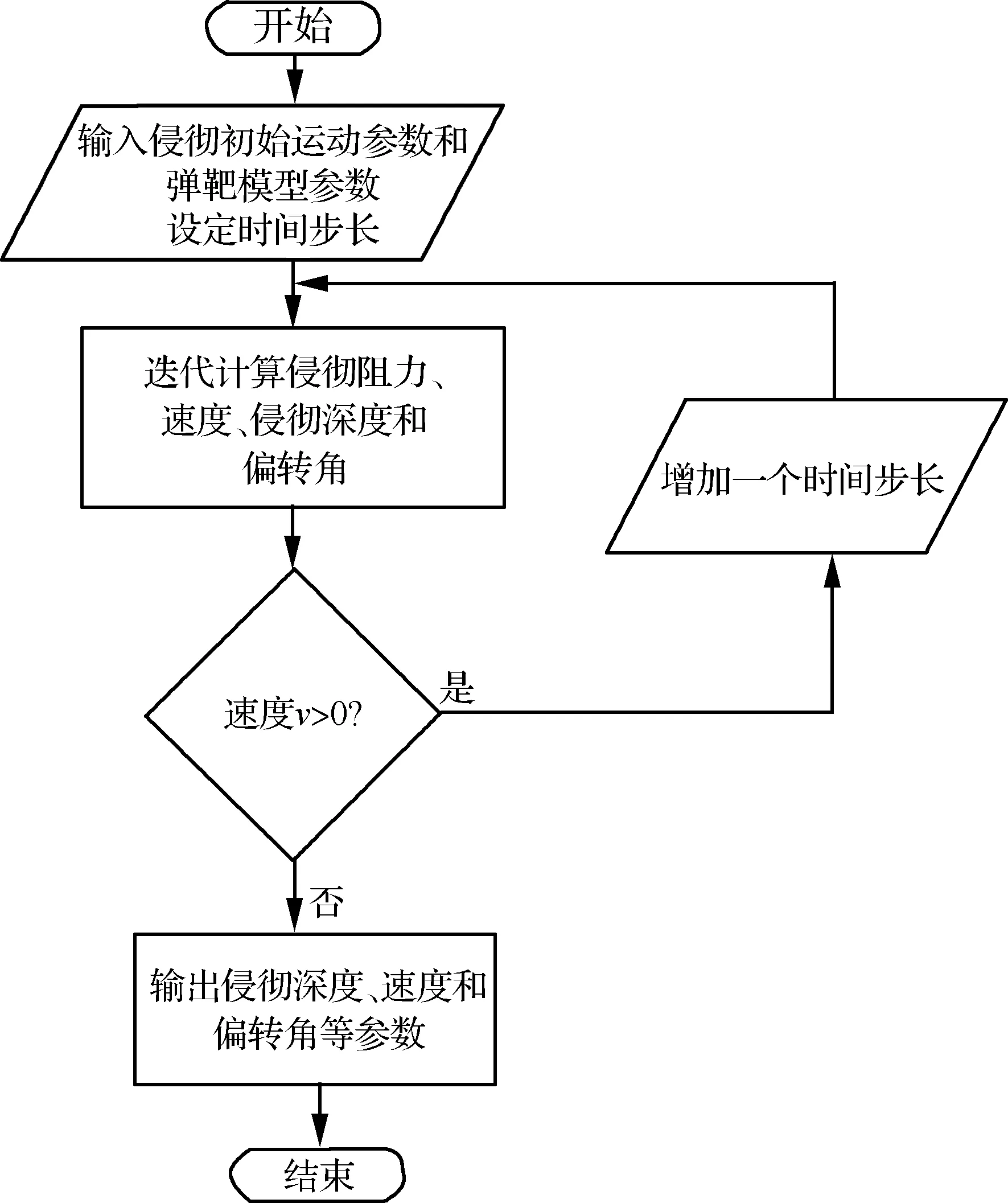
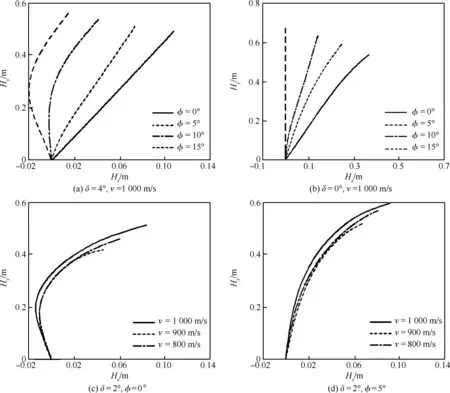
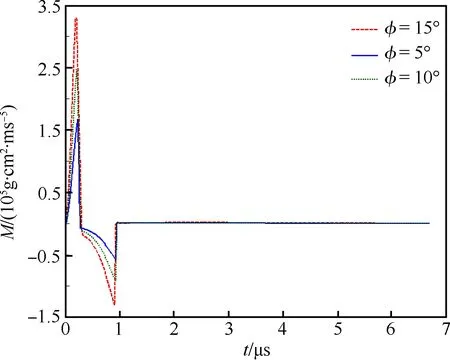
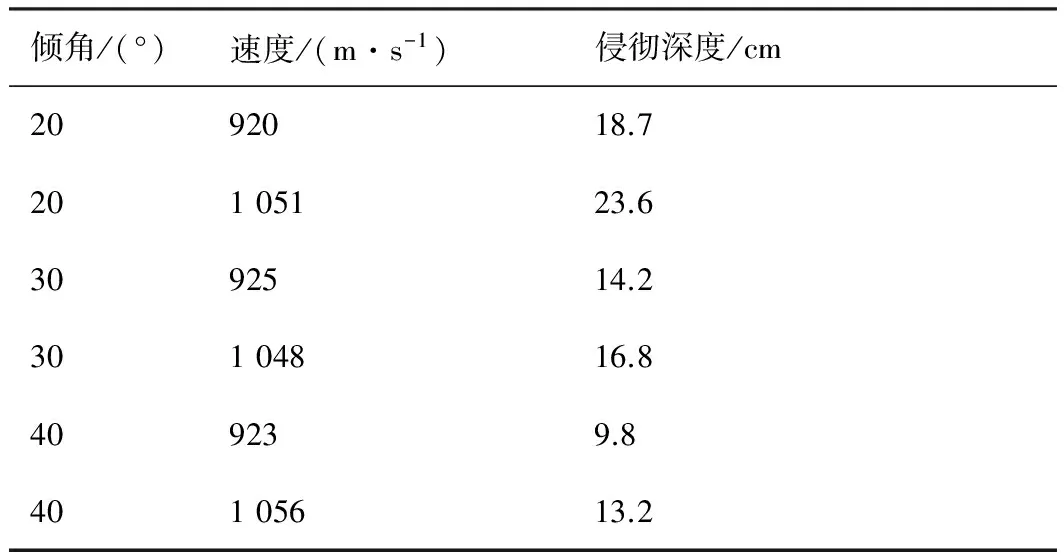
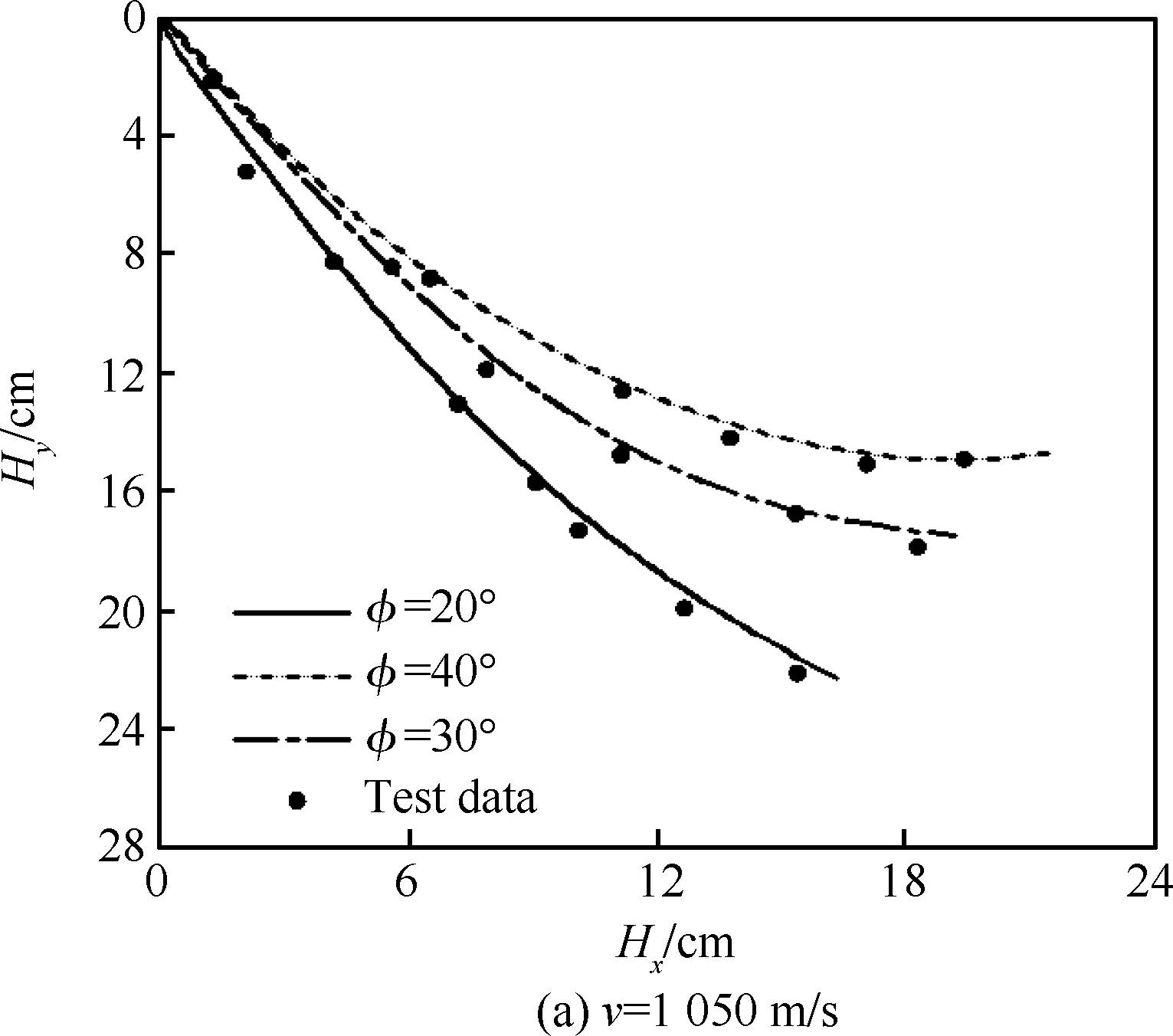
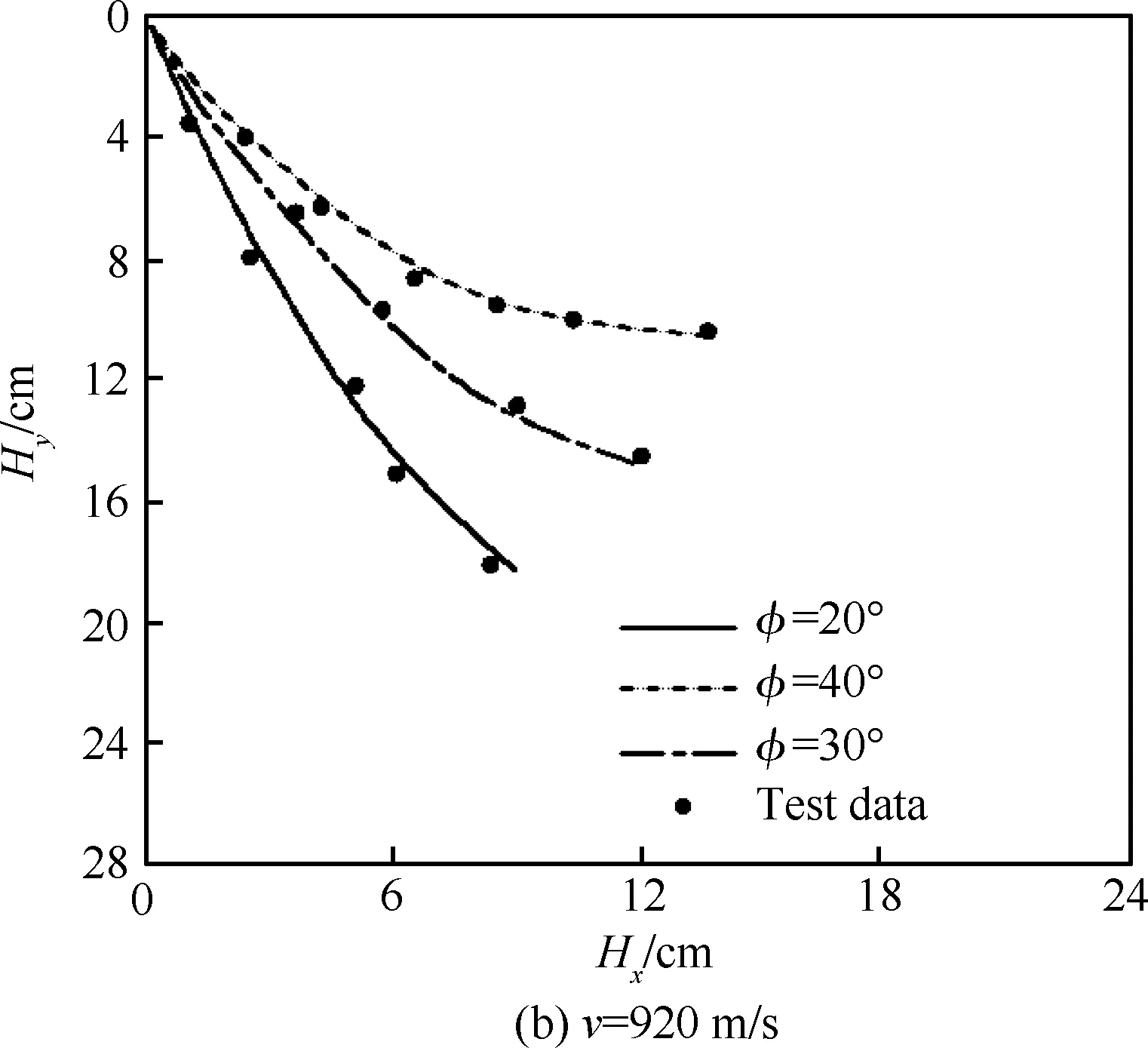
当R′ (31) (32) (33) (34) 当R′=a时,y1 (35) (36) (37) (38) 最终弹体所受的阻力和阻力矩分别为 Fx1=∬SdFx1dA=Fx1,2-Fx1,1 (39) Fy1=∬SdFy1dA=Fy1,2+Fy1,1 (40) Mx1=∬SdMx1dA=Mx1,2-Mx1,1 (41) My1=∬SdMy1dA=My1,2-My1,1 (42) 将4个阶段分别加以讨论。 侵彻的第1阶段: (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) 式中:yo′为在x2o′y2内的弹体质心纵向偏移量。 (53) (54) 侵彻的第2阶段: (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) 式中: (74) (75) 侵彻的第4阶段: (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) 1.6运动方程的求解与分析 弹体质心轴处所受的阻力矩为 M=Mx1+My1 (92) 将Fx1和Fy1分别向弹体质心运动方向投影,得到靶体阻力为 Fs=Fx1sin δ+Fy1cos δ (93) Fc=Fx1cos δ-Fy1sin δ (94) 弹体头部顶点运动微分方程为 (95) 式中:Hx和Hy分别为弹体顶点的水平位移和垂直位移。 1.7计算结果 采用质量为5.9 kg,弹径为76.2 mm,曲率比为4的钻地弹,混凝土抗剪屈服强度为95 MPa,密度为2 240 kg/m3,锁变压缩体积应变为0.04。利用MATLAB程序计算了钻地弹以不同倾角、攻角和速度侵彻混凝土的弹头运动轨迹,流程图如图8所示。计算结果如图9所示,从图9(a)中当攻角为4°、倾角为0°时,以及图9(c)中攻角为2°、倾角为0°,在侵彻初期,由于惯性的作用,弹体大致沿速度的方向前进,在着靶的瞬间,弹体产生一偏转力矩,该偏转力矩和由于斜侵彻产生靶体对弹体的不对称力使得弹体在侵彻方向前进的同时,逐渐发生偏转,直至动能消失或者弹体头部所受的约束对称时,弹体停留在靶体内部。弹体攻角对侵彻轨迹有显著的影响,因此为了提高侵彻效果,应尽量减小或者消除攻角。当攻角为零时,弹体侵彻深度随着倾角的增加而减小,偏转加剧。当攻角与倾角一定时,提高侵彻速度可以减小弹道偏转,因此为了提高侵彻威力,应适当提高侵彻速度。图10为弹体侵彻初期的偏转力矩,从图中可以看出,偏转力矩在初始阶段随着侵彻时间而增加,达到最大值后开始下降,降低至零值后转为反方向力矩,随着弹体头部约束对称,偏转力矩为零。通过对比可知,弹体在不同倾角下由于偏转力矩在侵彻中幅值和作用时间不同,形成不同的侵彻偏转弹道。 图8 程序流程图Fig.8 Program flowchart 图9 弹体头部运动轨迹Fig.9 Trajectory of projectile head 图10 偏转力矩时程图Fig.10 Deflection torque vs time 由于攻角侵彻试验数据比较难进行,本文进行了弹体倾角侵彻混凝土靶的试验,如图11所示,采用小口径滑膛炮加速弹体运动,撞击安放在架子上的混凝土靶,用测速仪记录着靶速度。弹体材料为高强度钢,弹径为10 mm,长径比为4,曲率比为3。混凝土靶直径为800 mm,用厚度为3 mm的钢板箍紧,靶板前表面预制成20°、30°、40°的倾角。 图11 现场布置图Fig.11 Site layout 弹体斜侵彻混凝土靶的试验结果如表1所示。 试验后的弹体和靶体如图12所示,弹体基本无变形,与混凝土的高温摩擦造成头部尖端轻微的变钝,弹身沾满白色混凝土粉末。在倾角较小时混凝土靶面破坏近似圆形,形成了相对于弹着点基本对称的弹坑区且正面无明显径向裂纹延伸到靶板外围,说明靶体可视为半无限靶条件,试验数据真实可靠,开坑深度约为2~3倍弹径。 图13为弹体速度为1 051 m/s、倾角为20°时的侵彻轨迹,为了使轨迹形状更加直观,将细铁丝紧贴弹体侵彻轨迹,并涂上红色墨水,从图中可看出侵彻弹道发生了一定程度的偏转。将试验数据与计算模型的结果进行比较,如图14所示,试验值与计算结果吻合较好。随着倾角的增大,弹体侵彻深度减小,弹道横向偏移量增加,弹道轨迹弯曲程度增加。 表1 试验结果 图12 试验后的弹体与混凝土靶Fig.12 Projectiles and concrete target after tests 图13 试验弹的运动轨迹Fig.13 Trajectory of test projectiles 图14 侵彻深度的试验结果与理论计算比较Fig.14 Comparison of penetration depth between test results and theoretical calculation 1) 考虑表面层裂机理对斜侵彻弹道的影响,推导出了非对称下卵形弹所受阻力和偏转力矩的计算式,将倾角和攻角结合起来考虑,得到了斜侵彻下的弹体运动轨迹,侵彻深度的计算结果与试验结果吻合较好。 2) 初始阶段弹体所受的阻力不对称,产生的偏转力矩瞬间增加,达到最大值后开始下降,降低至零值后转为反方向力矩,随着弹体头部约束的对称,偏转力矩为零。 3) 弹体以不同倾角侵彻混凝土靶,侵彻深度随倾角的增大而明显减小,横向偏移量也随之增大,弹体头部运动轨迹的弯曲弧度也越大。 4) 弹体攻角对侵彻轨迹有显著的影响,因此为了提高侵彻效果,应尽量减小或者消除攻角。当攻角与倾角一定时,提高侵彻深度可以减小弹道偏转,因此为了提高侵彻威力,应适当提高侵彻速度。 [1]BENMARD R S, CREIGHTON D C. Projectile penetration in soil and rock: Analysis for non-normal impact: AD-A081044[R]. Vicksburg, MI: Army Engineer Waterways Experiment Station, 1979: 11-27. [2]ROISMAN I V, YARIN A L, RUBIN M B. Oblique penetration of rigid projectile into an elastic-plastic target[J]. International Journal of Impact Engineering, 1997, 19(9-10): 769-795. [3]FORRESTAL M J, ALTMAN B C, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose steel projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4): 395-405. [4]FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectile[J]. International Journal of Impact Engineering, 1996, 18(5): 465-476. [5]MACEK R W, DUFFEY T A. Finite cavity expansion method for near-surface effects and layering during earth penetration[J]. International Journal of Impact Engineering, 2000, 24(3): 239-258. [6]LONGCOPE D B, TABBARA M R, JUNG J K. Modeling of oblique penetration into geologic targets using cavity expansion penetrator loading with target free-surface effects: SAND 99-1104C[R]//Albuquerque, NM: Sandia Nation Laboratories, 1999. [7]WARREN T L, HANCHAK S J, POORMON K L. Penetration of limestone targets by ogive-nosed VAR 4340 steel projectiles at oblique angles: Experiments and simulations[J]. International Journal of Impact Engineering, 2004, 30(10): 1307-1331. [8]高世桥, 刘杰明, 谭惠民. 侵彻弹倾斜侵彻半无限混凝土目标时的动力分析[J]. 兵工学报, 1995(4): 46-50. GAO S Q, LIU J M, TAN H M. Dynamical analysis of oblique penetration of a projectile against half-infinite concrete[J]. Acta Armamentarii, 1995(4): 46-50 (in Chinese). [9]李进忠, 蔡汉文, 崔秉贵, 等. 混凝土侵彻的工程计算模型[J]. 兵工学报, 1995(4): 86-88. LI J Z, CAI H W, CUI B G, et al. An engineering calculation model for the penetration in concrete targets[J]. Acta Armamentarii, 1995(4): 86-88 (in Chinese). [10]尹放林, 王明洋, 钱七虎, 等. 弹丸斜入射对侵彻深度的影响[J]. 爆炸与冲击, 1998, 18(1): 69-76. YIN F L, WANG M Y, QIAN Q H, et al. Penetration depth of projectile oblique into concrete[J]. Explosion and Shock Waves, 1998, 18(1): 69-76 (in Chinese). [11]张刚明, 许沭华, 王肖钧, 等. 细长弹在混凝土地面中斜侵彻过程的工程近似分析[J]. 弹道学报, 1999, 11(3): 14-19. ZHANG G M, XU S H, WANG X J, et al. Engineering analysis of the oblique penetration of concrete target by slender projectile[J]. Journal of Ballistics, 1999, 11(3): 14-19 (in Chinese). [12]何涛. 动能弹在不同材料靶体中的侵彻行为研究[D]. 合肥: 中国科学技术大学, 2007: 88-102. HE T. A study on the penetration of projectiles into targets made of various materials[D]. Hefei: University of Science and Technology of China, 2007: 88-102 (in Chinese). [13]CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics[J]. International Journal of Impact Engineering, 2002, 27(5): 619-637. [14]武海军, 黄风雷, 王一楠. 高速弹体非正侵彻混凝土试验研究[C]//第八届全国爆炸力学学术会议文集. 北京: 北京理工大学, 2007: 488-494. WU H J, HUANG F L, WANG Y N. Experimental research on high-velocity penetration into concrete targets[C]//Proceeding of the 8th Chinese Conference on Explosion Mechanics. Beijing: Beijing Institute of Technology, 2007: 488-494 (in Chinese). [15]马爱娥, 黄风雷. 弹体斜侵彻钢筋混凝土的试验研究[J]. 北京理工大学学报, 2007, 27(6): 482-486. MA A E, HUANG F L. Experimental research on oblique penetration into reinforced concrete[J]. Transactions of Beijing Institute of Technology, 2007, 27(6): 482-486 (in Chinese). [16]吕中杰, 徐钰巍, 黄风雷. 弹体斜侵彻混凝土过程中的方向偏转[J]. 兵工学报, 2009, 30(2): 301-304. LV Z J, XU Y W, HUANG F L. Transverse deflection of projectile obliquely penetrating into concrete[J]. Acta Armamentarii, 2009, 30(2): 301-304 (in Chinese). [17]吴昊, 方秦, 龚自明, 等. 考虑刚性弹弹头形状的混凝土(岩石)靶体侵彻深度半理论分析[J]. 爆炸与冲击, 2012, 32(6): 573-580. WU H, FANG Q, GONG Z M, et al. Semi-theoretical analyses for penetration depth of rigid projectiles with different nose geometries into concrete (rock) targets[J]. Explosion and Shock Waves, 2012, 32(6): 573-580 (in Chinese). [18]王可慧, 宁建国, 李志康, 等. 高速弹体非正侵彻混凝土靶的弹道偏转试验研究[J]. 高压物理学报, 2013, 27(4): 561-566. WANG K H, NING J G, LI Z K, et al. Ballistic trajectory of high-velocity projectile obliquely penetrating concrete target[J]. Chinese Journal of High Pressure Physics, 2013, 27(4): 561-566 (in Chinese). [19]彭永, 方秦, 吴昊, 等. 不同头部形状弹体侵彻混凝土靶体的终点弹道参数分析[J]. 兵工学报, 2014, 35(2): 128-134. PENG Y, FANG Q, WU H, et al. Theoretical analyses for terminal ballistic of the projectiles with different nose geometries penetrating into concrete targets[J]. Acta Armamentarii, 2014, 35(2): 128-134 (in Chinese). [20]WEN H M, YANG Y. A note on the deep penetration of projectile into concrete[J]. International Journal of Impact Engineering, 2014, 66(4): 1-4. [21]王明洋, 郑大亮, 钱七虎. 弹体对混凝土介质侵彻、贯穿的比例换算关系[J]. 爆炸与冲击, 2004, 24(2): 108-114. WANG M Y, ZHENG D L, QIAN Q H. The scaling problems of penetration and perforation for projectile into concrete media[J]. Explosion and Shock Wave, 2004, 24(2): 108-114 (in Chinese). [22]宁建国. 爆炸与冲击力学[M]. 北京: 国防工业出版社, 2010: 298-300. NING J G. Explosion and impact mechanics[M]. Beijing: National Defense Industry Press, 2010: 298-300 (in Chinese). 薛建锋男, 博士研究生。主要研究方向: 弹体战斗部设计。 Tel: 025-84317237 E-mail: xuejianfeng666@163.com 沈培辉男, 教授, 硕士生导师。主要研究方向: 战斗部设计。 Tel: 025-84317237 E-mail: sphjy8@mail.njust.edu.cn 王晓鸣男, 教授, 博士生导师。主要研究方向: 弹药与战斗部系统技术。 Tel: 025-84315059 E-mail: 202xm@163.com Engineering calculation model for oblique penetration into concrete target by earth penetration weapon XUE Jianfeng, SHEN Peihui*, WANG Xiaoming School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing210094, China In order to study trajectory of earth penetration weapon during penetration under stress asymmetry, in combination of kinetic basic equations and classical cavity expansion theory, an engineering model of projectile penetrating into concrete with incident angle and yawed angle is established using surface splitting mechanism. The relationship between the trajectory of projectile head and yawed angle, incident angle and velocity is obtained using the model. The results show that the penetration depth decreases obviously with the increase of incident angle, and the curve arc of the projectile’s head is larger. The deflection torque increases with the increase of yawed angle. The engineering model is verified by experiment, and the results are in good agreement with the experimental results. The model can effectively reflect the main characteristics of oblique penetration process. The applicability and rationality of the model are also proved. impact dynamics; earth penetration weapon; oblique penetration; splitting mechanism; trajectory 2015-12-17; Revised: 2016-01-20; Accepted: 2016-01-25; Published on line: 2016-02-1816:18 National Basic Research Program of China (61314302) . Tel.: 025-84317237E-mail: sphjy8@mail.njust.edu.cn 2015-12-17; 退修日期: 2016-01-20; 录用日期: 2016-01-25; 时间: 2016-02-1816:18 www.cnki.net/kcms/detail/11.1929.V.20160218.1618.002.html 国家“973”计划(61314302) .Tel.: 025-84317237 E-mail: sphjy8@mail.njust.edu.cn 10.7527/S1000-6893.2016.0031 V219; TJ014 A 1000-6893(2016)06-1899-13 引用格式: 薛建锋, 沈培辉, 王晓鸣. 钻地弹斜侵彻混凝土靶的工程计算模型[J]. 航空学报, 2016, 37(6): 1899-1911. XUE J F,SHEN P H, WANG X M. Engineering calculation model for oblique penetration into concrete target by earth penetration weapon[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1899-1911. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn URL: www.cnki.net/kcms/detail/11.1929.V.20160218.1618.002.html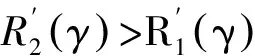
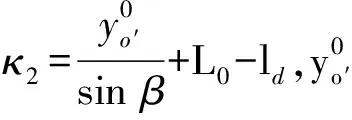
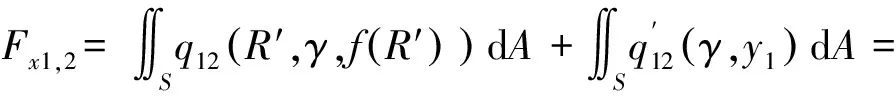
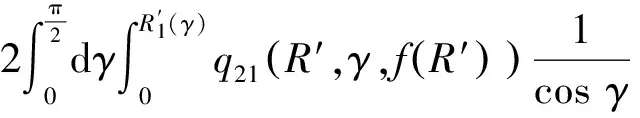
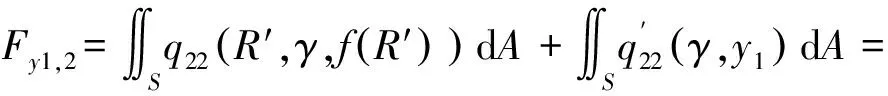
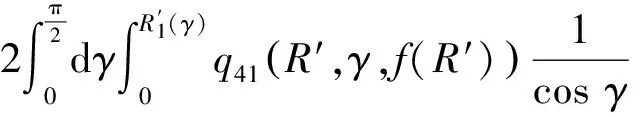
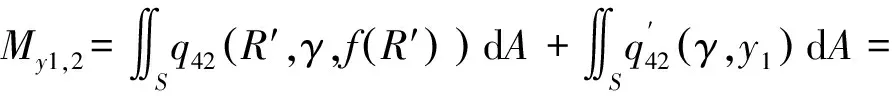
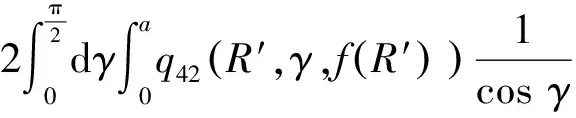
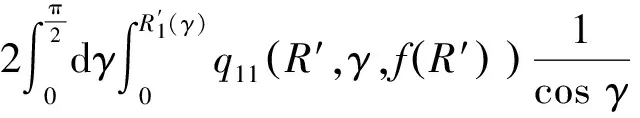
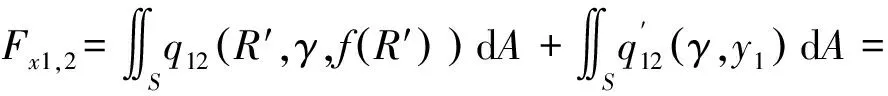

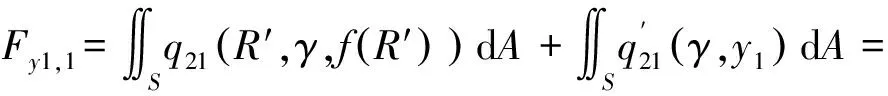
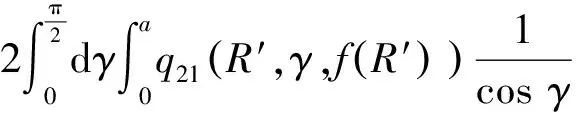
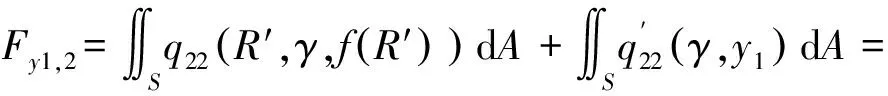
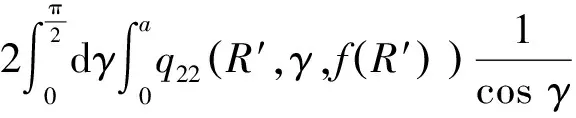
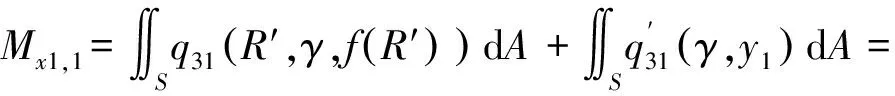

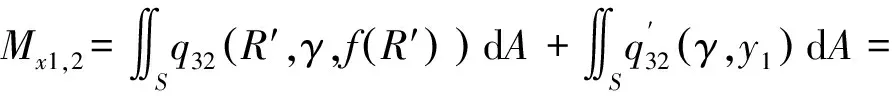
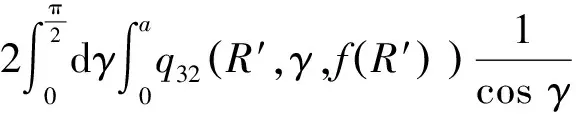
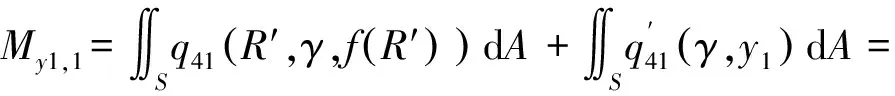
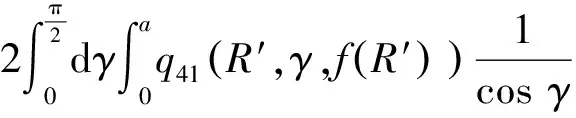
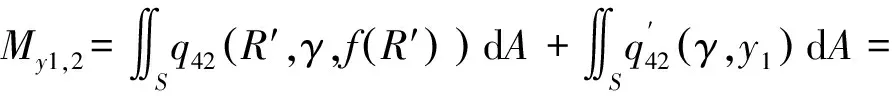
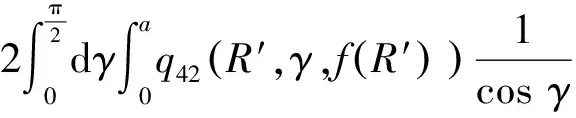
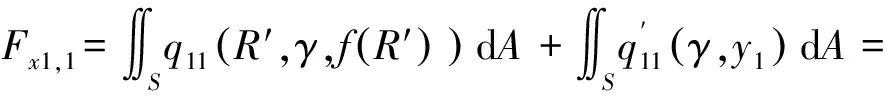
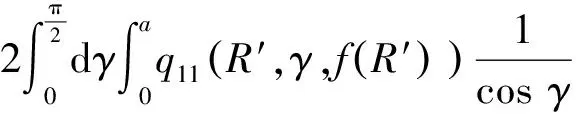
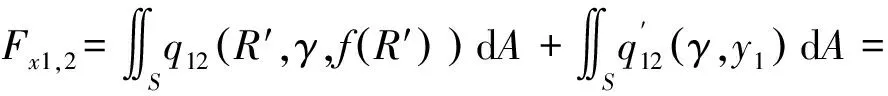

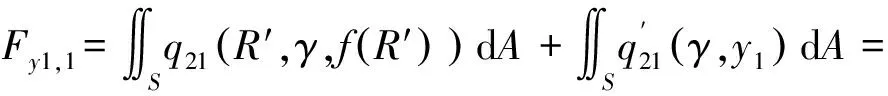

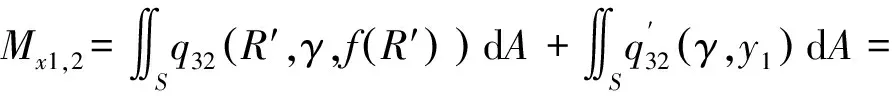
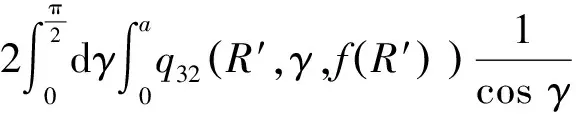
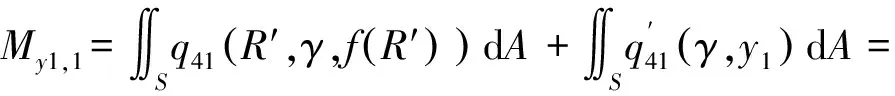
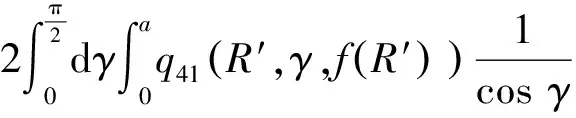
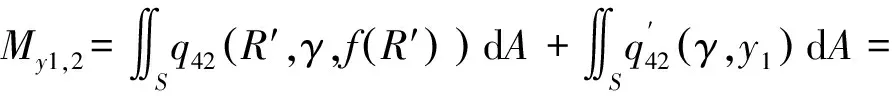
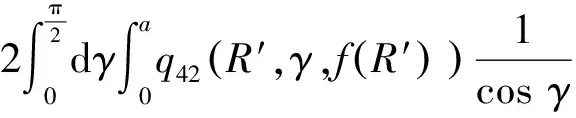
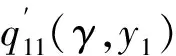
2 试验研究

3 结果与讨论


4 结 论

