1 200 ℃高温环境下板结构热模态试验研究与数值模拟

吴大方， 王岳武， 商兰， 蒲颖， 王怀涛

北京航空航天大学 航空科学与工程学院， 北京　100083



1 200 ℃高温环境下板结构热模态试验研究与数值模拟

吴大方*， 王岳武， 商兰， 蒲颖， 王怀涛

北京航空航天大学 航空科学与工程学院， 北京100083

高超声速飞行器高马赫数飞行时，翼、舵及垂尾等板形姿态控制结构将会面临极为严酷的高温环境，为了获得难于实测的结构在高温与振动复合环境下的热模态参数，本文将瞬态气动热试验模拟系统与振动试验系统相结合，建立了高温热/振联合试验测试系统，实现了高达1 200 ℃热环境下矩形板结构的模态频率等关键振动参数的试验测试。同时，对矩形板结构的热模态特性进行了数值计算，并将试验结果与计算结果进行对比验证。试验中通过自行研制的耐高温陶瓷导杆引伸装置将结构上的振动信号传递至高温热场之外，使用常温加速度传感器对振动信号进行参数识别；并运用时-频联合分析技术对试验数据进行分析处理。本文所获得的高温环境(200～1 100 ℃)下矩形板结构的模态频率的试验结果与数值计算结果取得了比较好的一致性，验证了本试验方法的可信性及可用性。本研究结果为高超声速飞行器翼舵结构在高温环境下的振动特性分析以及安全可靠性设计提供了重要的试验手段和参考依据。

高超声速飞行器； 热模态试验； 数值计算； 高温环境； 振动特性

高超声速飞行器能够以超过5倍声速的速度(马赫数>5)飞行，由气动加热产生的热环境极为严酷。某些高超声速飞行器翼、舵等姿态控制结构表面所面临的热环境会超过1 000 ℃，飞行器前端、翼舵前缘部的温度则会更高[1]。另外，由于远程高超声速飞行器飞行速度快、滞空时间长，在飞行过程中翼、舵等姿态控制结构还会出现持续的剧烈振动。气动加热产生的高温使得飞行器材料和结构的弹性性能发生变化，从而引起翼舵结构的模态频率、模态振型等振动特性的改变，这会对高超声速飞行器的颤振特性和控制特性产生很大的影响。因此研究翼、舵等平面状结构在力-热复合环境下的模态频率等振动特性随温度的变化规律，对高超声速飞行器的安全飞行和可靠性设计具有非常重要的意义。

目前国内外已有很多人对航空航天结构的热振动问题进行了理论分析与数值计算的研究工作，Lee等[2]通过数值模拟的方法，研究了不同温度下超声速气流中的碳纤维环氧复合材料加筋板的颤振特性。Brown[3]对X-34发动机喷管在高温环境下的模态和固有频率进行了分析计算。Chakraverty和Pradhan[4]使用瑞利-里茨法(Rayleigh-Ritz Method)计算了功能梯度复合材料板在高温环境下的模态频率和模态振型。Fan和Wang[5]使用摄动法研究了碳纳米管增强复合材料梁在高温环境下的模态频率等振动特性。由于理论必须以实验为基础，计算所得的结果也需要经过实验验证，因此通过热/振联合试验获取结构在恶劣高温环境下的振动特性参数极为重要。

早在1955年，NACA 兰利航空实验室的Vosteen等[6-7]针对飞行器翼结构在非均匀温度场中的固有频率特性进行了试验研究，试验温度环境为139 ℃。1960年NACA兰利研究中心的McWithey和Vosteen[8]对X-15的翼面结构在热环境下的振动性能进行了试验研究，翼面结构的主体温度为347 ℃。1991年Kehoe和Snyder[9-10]使用激光测振仪，测量了平板结构的热模态频率和模态振型，热环境温度为245 ℃。当今，随着高速飞行器速度的不断提升，外边界的温度环境变得越来越恶劣，设计部门迫切希望能够通过试验获得更高温度环境下的结构热模态参数。2010年NASA德莱顿飞行研究中心使用耐高温加速度传感器对高超声速飞行器X-37的C/SiC方向舵的振动特性参数进行了试验测试。耐高温加速度传感器具有安装使用方便的优点，可直接得到测量点处的振动信号，但是针对不同的温度区段需要对测试结果进行修正，测量精度受温度环境因素的影响比较大，并且最高使用温度范围受制于传感器的温度使用极限。因此，NASA实现的上述热模态试验的温度环境为482 ℃[11]。而实际上飞行速度可高达25倍声速的X-37的翼面温度要远大于482 ℃，这说明要实现更高温度的热模态试验测试还需要研制温度极限更高的新型加速度传感器，或者采用其他的测试方法。2011年韩国国防发展局和忠南国立大学使用非接触式激光测振方法对矩形平板结构进行了热模态试验，其实现温度为500 ℃[12]。2015年北京强度环境研究所对悬挂状态的平板使用激光测振仪进行了热模态试验，获得了500 ℃热环境下方形平板的热模态参量[13]。在上述采用激光测振方法的文献[12-13]中，为了避免热源发出的强光干扰激光测振仪，仅对平板试验件实施单侧面加热，在非加热面对试验数据进行采集。这种单侧面加热与飞行器翼、舵等结构双侧面同时受热的热环境不同，事实上能够实现双侧面同时加热并进行热模态试验测试要比单侧面加热测试困难得多。除此之外，还可见到少量试验温度为500 ℃左右的热/振联合试验的研究文献[14-16]。若要大幅度提升热模态试验的温度环境，实现高超声速飞行器高达1 200 ℃的恶劣温度环境下的翼、舵等结构的热振动参数测试，并能与计算结果进行比较，是一个具有挑战性的工作。虽然笔者近年来对500 ℃以上的热模态试验方法进行过研究[17-18]，但是，未能进行理论计算和试验结果之间的对比验证。而计算结果和试验结果的互相支撑和验证，对确立试验方法的可信性和可用性极为重要。目前可实现高达1 200 ℃严酷高温环境下的热模态试验测试，并能将试验所得结果与计算结果进行对比验证的研究工作还未见报道。

本文将高温瞬态气动热试验模拟系统与振动试验系统相结合，建立能够实现高达1 200 ℃高温下的热/振联合试验系统。采用红外辐射方式生成可控的双侧面同步加热环境，并通过激振装置对单端固支矩形板结构的自由端实施振动激励。自行设计制作专用刚性耐高温引伸装置，将矩形板结构上的振动信号传递到高温热场之外，再使用常温加速度传感器获取高达1 200 ℃热环境下矩形板结构的模态频率、模态振型等重要特性参数。同时本文对矩形板结构的热模态特性进行数值计算，将试验结果和数值计算结果进行对比验证，确认试验方法的可信性和可用性。

1　试验件、试验装置与试验方法

1.1试验件

为了将试验结果和计算结果进行对比验证，试验件选择为如图1所示的矩形板结构，所用材料为耐高温镍基不锈钢(1Cr18Ni9Ti)，试验件长为340 mm，宽为220 mm，厚为7.5 mm。矩形板垂直焊接在安装支座上，通过螺栓与竖梁连接形成单端固支的悬臂结构，为了在试验中获取试验件上的振动响应信号，在矩形板的4个截面上开有8个直径为5 mm的圆孔，用于安装耐高温的振动信号引伸测量组件，孔的位置分布如图1(b)所示。矩形板试验件的自由端有一个直径为8 mm的激励导杆安装孔，激振器处于矩形板试验件自由端的下方，由金属导杆和螺栓与矩形板试验件连接。试验时激振器通过金属导杆在热场之外对矩形板悬壁结构进行振动激励。矩形板试验件外表面中部区域的上、下对称部位安装有一对温度传感器，用于试验件表面温度的测量与控制。图1(c) 为矩形板试验件的实物照片。

图1　矩形板结构试验件示意图Fig.1　Schematic for rectangular plate structure specimen

1.2试验装置

图2　热/振联合试验装置示意图Fig.2　Schematic of thermal/vibration joint test setup

热/振联合试验装置如图2所示，矩形板结构试验件水平放置，通过支座上的螺栓固定在竖梁上，在距离试验件的上、下表面各约60 mm处安装有密集排列的石英灯红外辐射加热阵列，对矩形板结构的上、下表面同时进行加热，瞬态气动热环境模拟试验系统生成稳态或动态变化的高温热试验环境。激振器安装在试验件自由端的下方，通过耐高温金属导杆与矩形板结构的端部连接，试验时激振器通过金属导杆在高温热场之外对试验件进行振动激励。由于试验温度非常高，将会达到 1 200 ℃的高温，并且加热试验时间比较长，为了防止高温环境下金属导杆强度降低，在金属导杆的中部区域设计安装有水冷结构，通过冷却水给金属导杆降温。另外，矩形板安装支座与竖直梁之间有一块带有水冷通道的金属热隔离板，试验时通过流动液体在试验件根部与竖梁之间形成一个温度缓冲区。为了对高温加热区域进行热屏蔽，红外辐射阵列的外侧安装有可耐1 600 ℃高温的轻质陶瓷纤维隔热板，以保证传感器、激振器以及供电线路的安全。

由于要在高达1 200 ℃的热环境下对矩形板结构的振动信号进行拾取，设计了由陶瓷引伸导杆和专用连接固定卡具组成的传递试验件振动信号的引伸装置。引伸导杆由耐高温的刚玉陶瓷材料制成，可在1 600 ℃的高温环境下稳定工作。陶瓷引伸杆的直径仅有4 mm，为中空结构，因此具有质量轻、刚性好的优点。由于刚玉陶瓷引伸导杆在高温下的抗变形能力很强，所以能够有效传递矩形板结构上的振动信号。为了获得矩形板结构上的热模态信息，在矩形板结构的4个截面上共安装了8组振动信号引伸装置(见图1)。引伸装置的一端固连在矩形板结构之上，另一端延伸至陶瓷纤维隔热板的外侧，用于采集振动信号的加速度传感器固定在处于常温环境中的引伸杆的冷端。因为加速度传感器被安装在热场之外，因此可以使用普通的常温加速度传感器获得难于测量的高温环境下的矩形板结构上的振动信号。

1.3热环境的生成

高温环境的生成使用自行研制的瞬态热试验控制系统，并将模糊控制和人工神经网络方法运用于热环境控制系统，使其能够按照温度或热流的变化对预设过程实施连续、快速、准确的非线性动态控制[19-21]。

本试验设计了如图3所示的12种不同的热环境，其中最高温度为1 200 ℃，其他依次为1 100、1 000、…、200、100 ℃。试验时热环境控制系统于220 s内将矩形板结构试验件的上、下表面同步加热到预设的目标温度，为了便于对远程高超声速飞行器的设计提供参考依据，所设定的热环境历程比较长，在试验件表面温度达到设定值之后，热控制系统将继续保持恒温至1 800 s，以获得如远程高超声速飞行器的翼、舵类结构在长时间热/振复合环境下的热模态参数的变化特性。由于1 200 ℃的温度条件已处于普遍使用的石英灯加热器极限能力的边缘，因此为了保证试验的安全性，高达1 200 ℃的设定加热时长为600 s，相对于其他温度历程要短一些。其主要目的是通过1 200 ℃的高温试验环境，观察和了解本矩形板结构的高温极限工作能力。

图3　预设温度环境Fig.3　Pre-set thermal environments

1.4振动激励系统

振动激励系统由加速度传感器、电荷放大器、模/数(A/D)转换器、控制计算机、数/模(D/A)转换器、功率放大器与激振器组成，其结构框图如图4(a)所示。控制计算机根据激励条件输出激振波形，然后经过数/模转换器变换为连续的电压信号，激励信号经功率放大器放大之后，驱动激振器使矩形板结构产生振动。由加速度传感器采集到的结构表面振动信号经过放大和模/数转换后输入到控制计算机中进行存储与分析处理。

在热环境控制系统对矩形板结构进行加热的同时，由信号发生器产生随机信号，经功率放大后驱动激振器对试验件的自由端实施连续的振动激励，图4(b)为部分随机振动激励波形。整个热/振联合试验过程中由计算机全程实时测量和记录矩形板悬臂结构上的各加速度传感器随时间和温度变化产生的动态响应信号。

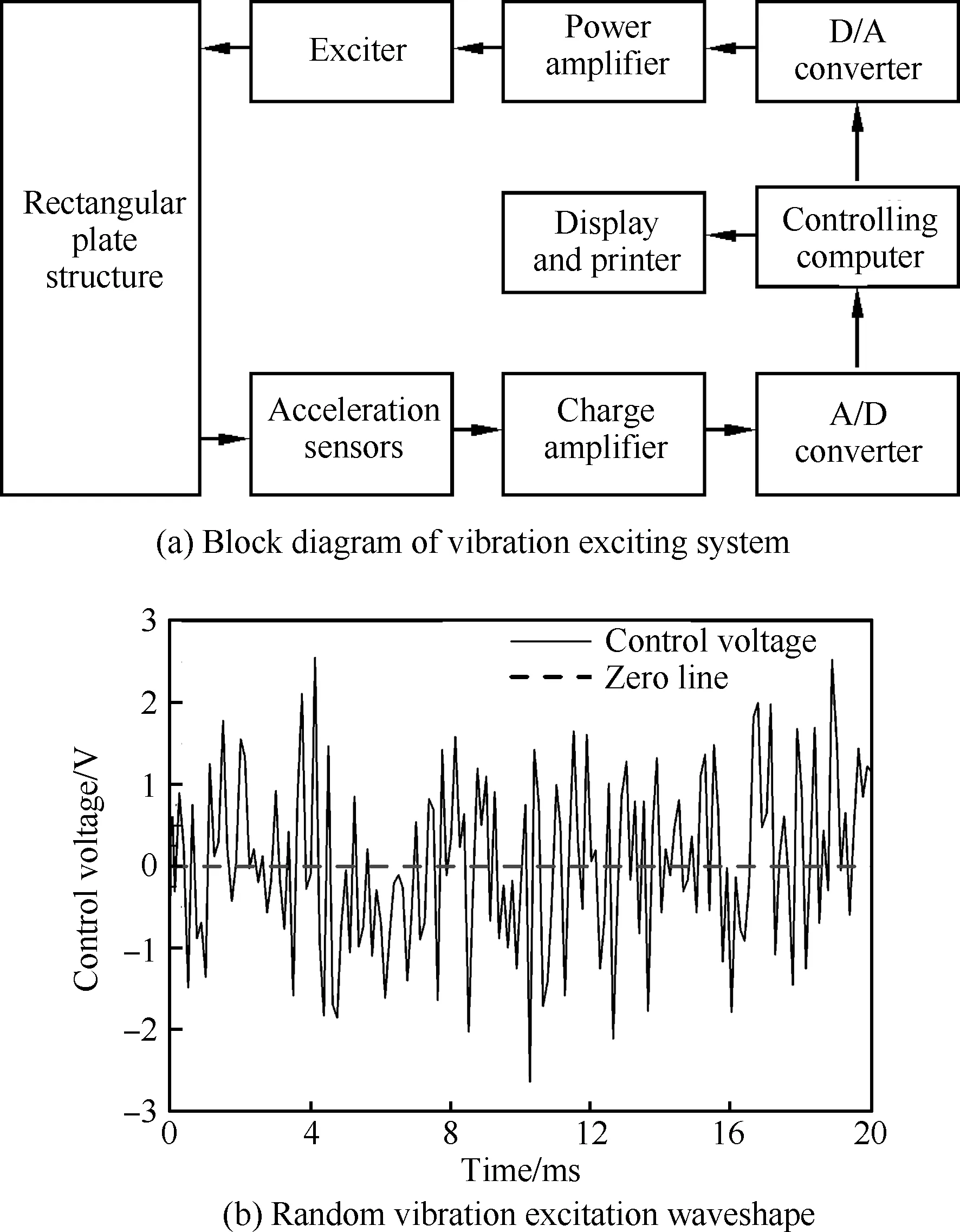
图4　振动激励系统及随机振动激励波形Fig.4　Vibration exciting system and random vibration excitation waveshape

1.5模态频率分析方法

热/振联合试验结束后，根据采集到的振动响应信号，采用时-频联合分析技术[22]得到与时间和温度相关的频响函数，进而获得各阶模态所对应的频率随温度变化的规律。其处理过程如下所述。

对激振器产生的激励信号x进行短时傅里叶变换(STFT),得

(1)

式中：n和m分别为第n和第m个离散数据；x(m)为离散化的振动激励信号序列；g(n-m)为时间窗口函数；ω为角频率；Gx(n,ω)为振动激励信号。

对试验过程中获得的加速度时间历程响应信号y实施短时傅里叶变换，得

(2)

式中：y(m)为离散化的加速度信号序列；Gy(n,ω)为加速度信号。通过式(1)和式(2)由短时傅里叶变换得到的振动激励信号Gx(n,ω)和加速度信号Gy(n,ω)，进而得到结构传递函数短时傅里叶变换H(n,ω)的表达式为

(3)

对式(3)中的H(n,ω)进行模态参数辨识及数据处理，即可得到模态频率随温度及时间的变化历程。

2　热/振联合试验结果

图5为热/振联合试验的照片。图6为热环境为100～1 200 ℃范围之内的12种不同温度条件下，矩形板结构上下表面的温度控制结果与预设温度的比较。由图6可见，在100～1 200 ℃的高温热/振联合试验中，矩形板结构上下表面的控制温度曲线与预设温度曲线均具有良好的吻合性。特别是，温度快速上升段无明显的热滞后现象，温度转折过渡段无明显的超调及振荡现象。表1给出了1 200 ℃高温环境下矩形板结构上下表面典型时刻的预设温度值和控制温度值。由表1 的试验数据可知，矩形板结构上下表面的控制温度与预设温度之间的相对误差小于0.5%，说明本热环境试验控制系统能够实现准确的动态跟踪，获得与预设温度吻合性良好的热环境模拟效果。

图5　热/振联合试验照片Fig.5　Photograph of thermal/vibration joint test

图6　矩形板结构表面的预设温度和控制温度曲线Fig.6　Pre-set and control temperature curves of rectangular plate structure surfaces

对采集到的加速度信号进行傅里叶变换，可获得矩形板在不同温度下的频谱曲线。图7给出了其中3种温度T环境下的频谱曲线。通过对各频谱曲线进行信号识别，获得了矩形板结构在不同温度下的前3阶模态频率的数值。

图8中的实线为1 100 ℃高温下测得的矩形板结构1阶模态频率的变化数据，从图中的测试数据可见，在前220 s的快速升温段，试验件的弹性模量随着温度的升高而降低，矩形板结构的模态频率也随着温度的升高而不断降低。当表面温度趋于稳定之后，试验件的力学性能参数会逐渐趋于稳定，因此模态频率的变化趋势也变得比较缓慢，逐渐趋于稳定状态。由于在动态激励和数据采集过程中存在宽带随机信号和频率分辨率等原因，实测得到的模态频率数据会出现小幅波动现象，因此，采用数据拟合方式进行平滑处理。采用分段拟合的方式对下降转折过渡段以及稳态段分别进行平滑拟合，拟合函数取为

表11 200℃ 高温环境下矩形板结构上、下表面典型时刻的预设温度和控制温度

Table 1Pre-set and control temperature on upper and lower surfaces of rectangular plate structure in 1 200 ℃ high-temperature environment at typical moment

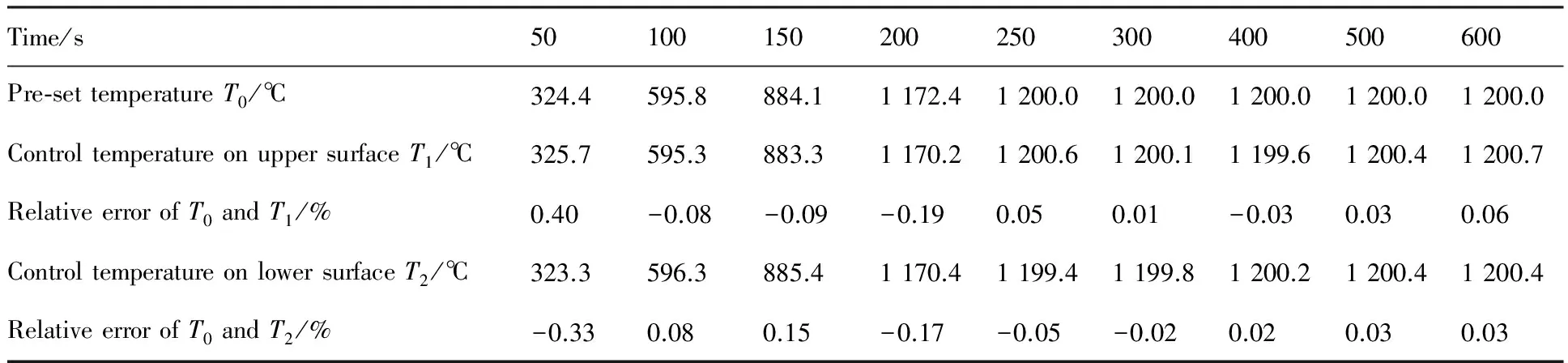
Time/s50100150200250300400500600Pre⁃settemperatureT0/℃324．4595．8884．11172．41200．01200．01200．01200．01200．0ControltemperatureonuppersurfaceT1/℃325．7595．3883．31170．21200．61200．11199．61200．41200．7RelativeerrorofT0andT1/%0．40-0．08-0．09-0．190．050．01-0．030．030．06ControltemperatureonlowersurfaceT2/℃323．3596．3885．41170．41199．41199．81200．21200．41200．4RelativeerrorofT0andT2/%-0．330．080．15-0．17-0．05-0．020．020．030．03

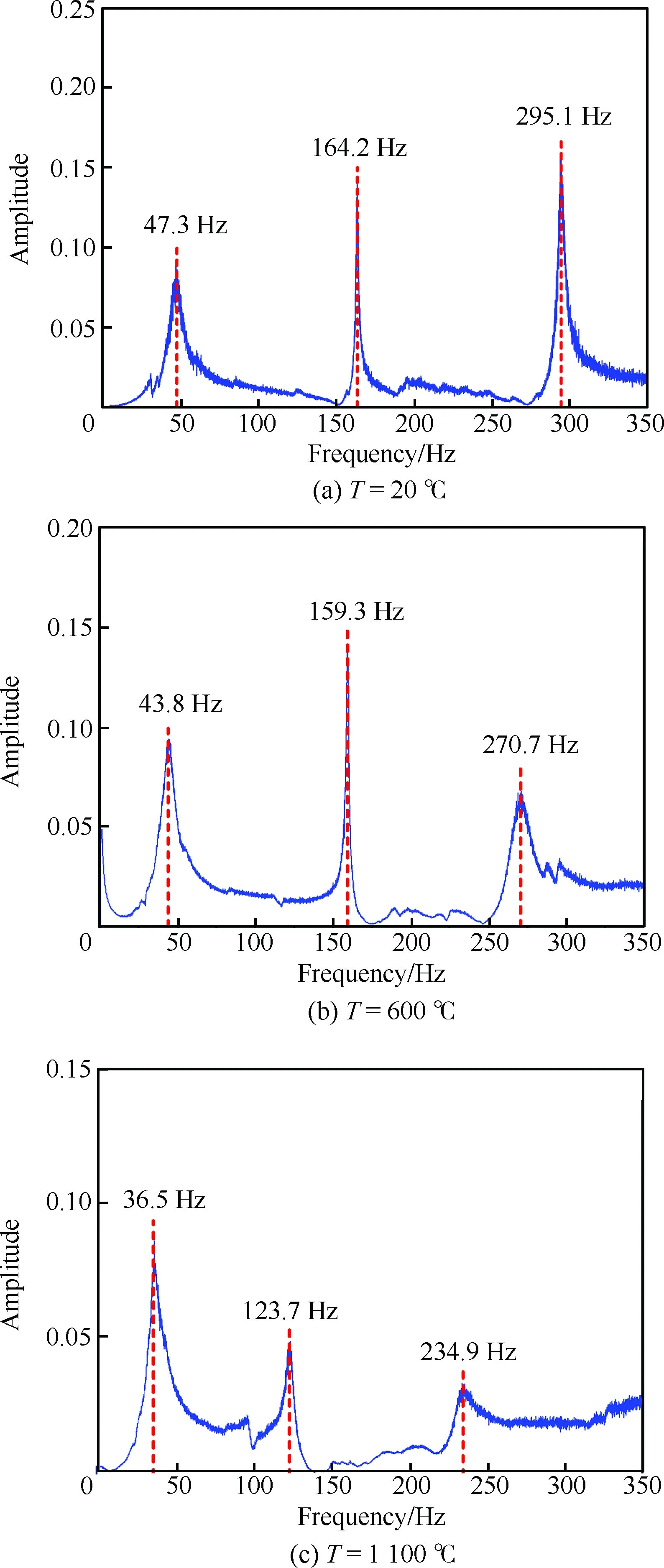
图7　不同温度下矩形板结构的频谱曲线Fig.7　Spectrum curves of rectangular plate structure at various temperatures　

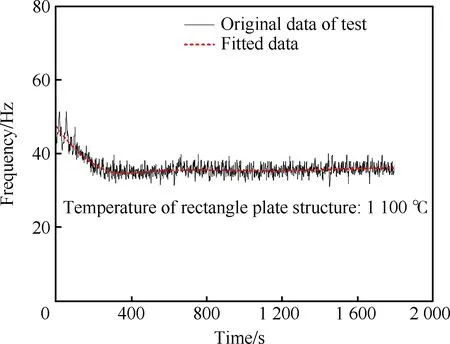
图8　矩形板结构的1阶固有频率变化曲线(1 100 ℃)Fig.8　Variation of first-order natural frequency curve of rectangular plate structure (1 100 ℃)

y=a0+a1t+…+aitii=0,1,…,n0

(4)

式中：y为模态频率；t为时间；ai(i=0,1,…,n0)为拟合系数，n0为多项式的阶数，根据模态频率的变化形态确定。

图8中的虚线为经过平滑拟合处理后的矩形板1阶模态频率的变化。另外，本试验对于在不同温度下测得的模态频率试验数据均按以上处理方式进行了相应的平滑拟合处理。

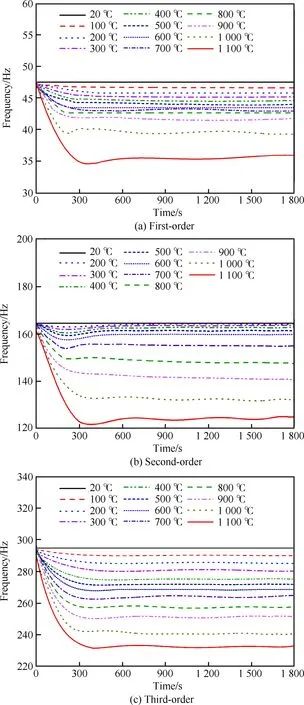
图9　矩形板结构的前3阶模态频率的变化曲线Fig.9　Variation curves of first-three order modal frequencies for rectangular plate structure

图9中给出了由热/振联合试验得到的20～1 100 ℃范围内矩形板结构的1～3阶模态频率随时间的变化曲线。由图9可见，在升温过程中，单边固支的矩形板结构的1～3阶模态频率均呈现下降趋势，升温速率越大，频率的变化越快；试验件的表面温度越高，模态频率的下降幅值越大，这主要是由高温环境下矩形板结构的弹性模量与结构刚度的变化所引起的。当试验件表面温度转入恒温阶段后，各阶模态频率的变化趋缓，逐渐接近一种相对比较稳定的状态。由图9知，温度在900 ℃以下变化时，不锈钢矩形板的1阶和3阶模态频率的变化幅度比较小，当温度超过900 ℃以后，1阶和3阶弯曲模态频率的变化明显增大。而对于2阶扭转模态，在600 ℃以下的温度范围内，其模态频率十分密集，曲线之间差别不是很明显。当温度超过600 ℃ 后，随着温度逐渐升高，模态频率的变化量明显增大(在图9(b)中略去了处于模态频率非常密集的温度区段内的100 ℃时的2阶模态频率曲线)。

另外，通过对安装在矩形板结构4个截面上的8只加速度传感器所获得的振动信号进行综合分析处理，得到了如图10所示的1 100 ℃高温环境下的1～3阶模态振型图，其中1阶和3阶为弯曲模态，2阶为扭转模态。通过试验获得的高温环境下的模态振型以及不同温度下矩形板结构模态频率的变化数据，为高超声速飞行器翼、舵等平面结构在热/振复合环境下的动特性分析提供了重要的参考依据。

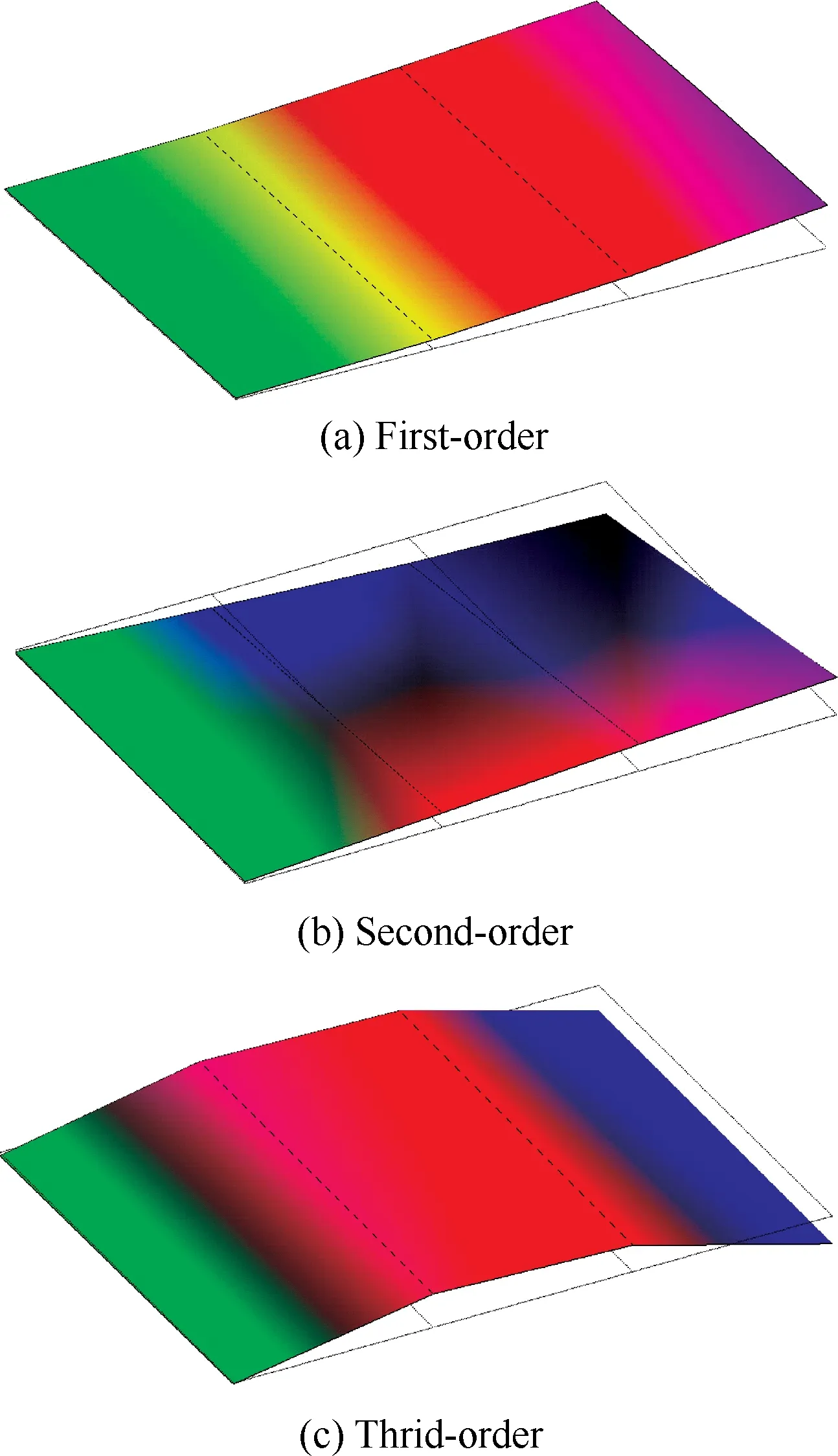
图10　矩形板结构的前3阶模态振型(1 100 ℃)Fig.10　First-three order modal shapes of rectangular plate structure (1 100 ℃)

图11中显示了1 200 ℃高温环境下1阶模态频率随时间的变化曲线。由图11可知，温度在900 ℃以下变化时，不锈钢矩形板的1阶模态频率的变化幅度比较小，当温度超过900 ℃以后，1阶模态频率的变化明显增大。图11中还显示出，1 200 ℃高温下矩形板结构的1阶模态频率相对于其他温度下的频率变化幅度出现了显著差别。首先，为了判断这种改变是否为偶然现象，本文进行了重复性的高温热/振联合试验(1 200 ℃-(1)和1 200 ℃-(2))。由图11可见，两次1 200 ℃下的1阶模态频率的变化趋势基本一致，数值相差很小，这说明1阶模态频率的变化趋势出现异常的现象不是偶然因素所导致，应该是该特定热环境下的真实试验表象。

图11　矩形板结构的1阶模态频率变化曲线(1 200 ℃)Fig.11　Variation of first-order modal frequency curves of rectangular plate structure (1 200 ℃)

另外，由图11中的曲线可见，两条1 200 ℃时矩形板结构的1阶模态频率曲线的下降幅值大幅度减少，1 200 ℃时的模态频率曲线不但明显高于1 100 ℃时的试验结果，在某些时间段内甚至还高于1 000 ℃时的1阶模态频率，此外，当试验件表面温度稳定之后(220 s之后)，1 200 ℃高温下的1阶模态频率呈现出比较明显的非稳定性的波浪形变化形态。造成这种现象的原因可能比较复杂，初步分析认为，1 200 ℃的高温环境已经超越了试验件的安全使用临界点，在1 200 ℃高温下,可能引起了矩形板结构某些部位的变形，导致了模态频率的变化出现异常。这种当温度达到一定数值后，模态频率的变化出现明显异常趋势的试验结果，对于确定该结构的安全使用极限具有重要的参考价值。

3　数值计算

3.1有限元模型

本文通过建立有限元模型，对矩形板结构在高温环境下的模态频率等参数进行了计算。模型的构建及运算基于有限元软件ANSYS，计算模型中的材料以及外形尺寸等参数与试验模型相同。有限元网格划分如图12所示，采用8节点壳单元(Shell 181)，总单元个数为2 992，节点数为3 105。矩形板材料(镍基高温合金1Cr18Ni9Ti)的密度为7 900 kg/m3,泊松比为0.25。

图12　矩形板的有限元网格划分Fig.12　Finite element mesh of rectangular plate

在数值计算中，通过求解式(5)所示的特征方程来获得板结构在高温环境下的模态参数。

(K-ω2M)Δ=0

(5)

式中：M为结构质量矩阵；ω为结构固有频率；Δ为结构模态向量；K为结构刚度矩阵。

高温环境会使材料的弹性性能发生改变，同时会使结构内部产生热应力，引起结构的屈曲变形。本文中悬臂板试验件的试验温度范围很宽，则有限元计算中应该考虑多种因素对振动特性的影响，如试验件的弹性性能在高温环境下的变化、试验件内部的热应力分布以及由结构变形引起的几何非线性等。因此，式(5)中的结构刚度矩阵可表示为

K=KT+Kσ+KNL

(6)

式中:KT为高温环境下材料弹性性能发生改变后的结构刚度矩阵；Kσ为考虑高温热应力对结构刚度影响的附加刚度矩阵；KNL为考虑几何非线性的悬臂板刚度矩阵。

式(6)中KT的表达式为

KT=∫ΩBTDTBdΩ

(7)

式中：B为形函数矩阵；DT为高温环境下反映材料弹性特性的矩阵。

式(6)中的Kσ为

Kσ=∫ΩGTSTGdΩ

(8)

式中：G为形函数的导数;ST为与试验件温度分布有关的应力矩阵。

式(6)中的KNL由线性部分BL和非线性部分BNL组成，KNL的表达式为

(9)

矩形板结构在高温环境下的模态频率等参数的有限元计算流程如图13所示。

图13　有限元计算流程图 Fig.13　Flowchart of finite element method (FEM)calculation

表2给出了计算过程中所需的室温至1 100 ℃ 温度范围内高温合金1Cr18Ni9Ti的弹性模量和热膨胀系数。由于文献[23]中仅给出了表2中800 ℃以内的数据，本文通过最小二乘法推导出其他温度下的材料弹性模量以及热膨胀系数的数值。

由于矩形板试验件的固支端安装有水冷隔离装置，且试验中通过流动的冷却水对固定支座进行降温，这使得试验件根部区域的温度比较低。因此试验件根部与中部区域之间形成了温度变化比较大的非均匀温度场。这种非均匀温度场会使矩形板结构的内部产生热应力，而且由于温度场的非均匀性，试验件各部分的力学性能也会有一定的差别，这在有限元计算中需要给予考虑。因此，在进行数值计算之前需要获得试验件表面各部分的温度分布状况，本文通过试验测试获取试件表面温度场的分布数据。

表2不同温度下高温合金1Cr18Ni9Ti的弹性模量和热膨胀系数

Table 2Elastic modulus and thermal expansion ratios of superalloys 1Cr18Ni9Ti at various temperatures

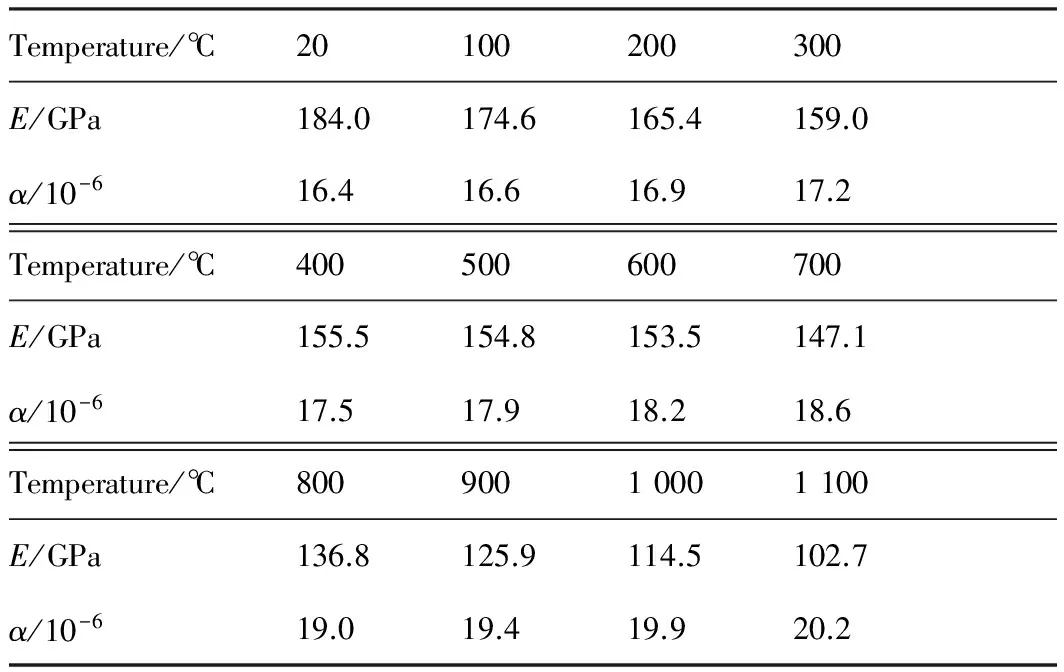
Temperature/℃20100200300E/GPa184．0174．6165．4159．0α/10-616．416．616．917．2Temperature/℃400500600700E/GPa155．5154．8153．5147．1α/10-617．517．918．218．6Temperature/℃80090010001100E/GPa136．8125．9114．5102．7α/10-619．019．419．920．2

3.2试验件表面的温度分布

为了得到矩形板上的温度分布，在试验件上表面安装了23只温度传感器，其位置和编号如图14 所示。温度测点主要有5行4列，各列之间的距离为30 mm。每一列均有5个温度测点，各行之间的距离为50 mm。由于矩形板垂直焊接在L型固定支座上，而且支座的质量比较大，因此试验时试验件根部的温度会比较低，于是在矩形板与固定支座的交界线处安装了一只温度传感器(1号)。矩形板上表面的控温点为23号传感器，矩形板下表面的相对位置有一个24号控温传感器。本试验通过中心线处安装的7个温度传感器(1，4，9，14，19，22，23)的测量数据可以得到矩形板中部x方向的温度变化情况。由4列温度传感器的测温数据可以得到矩形板的两个外边界与中轴线处的温度变化情况。

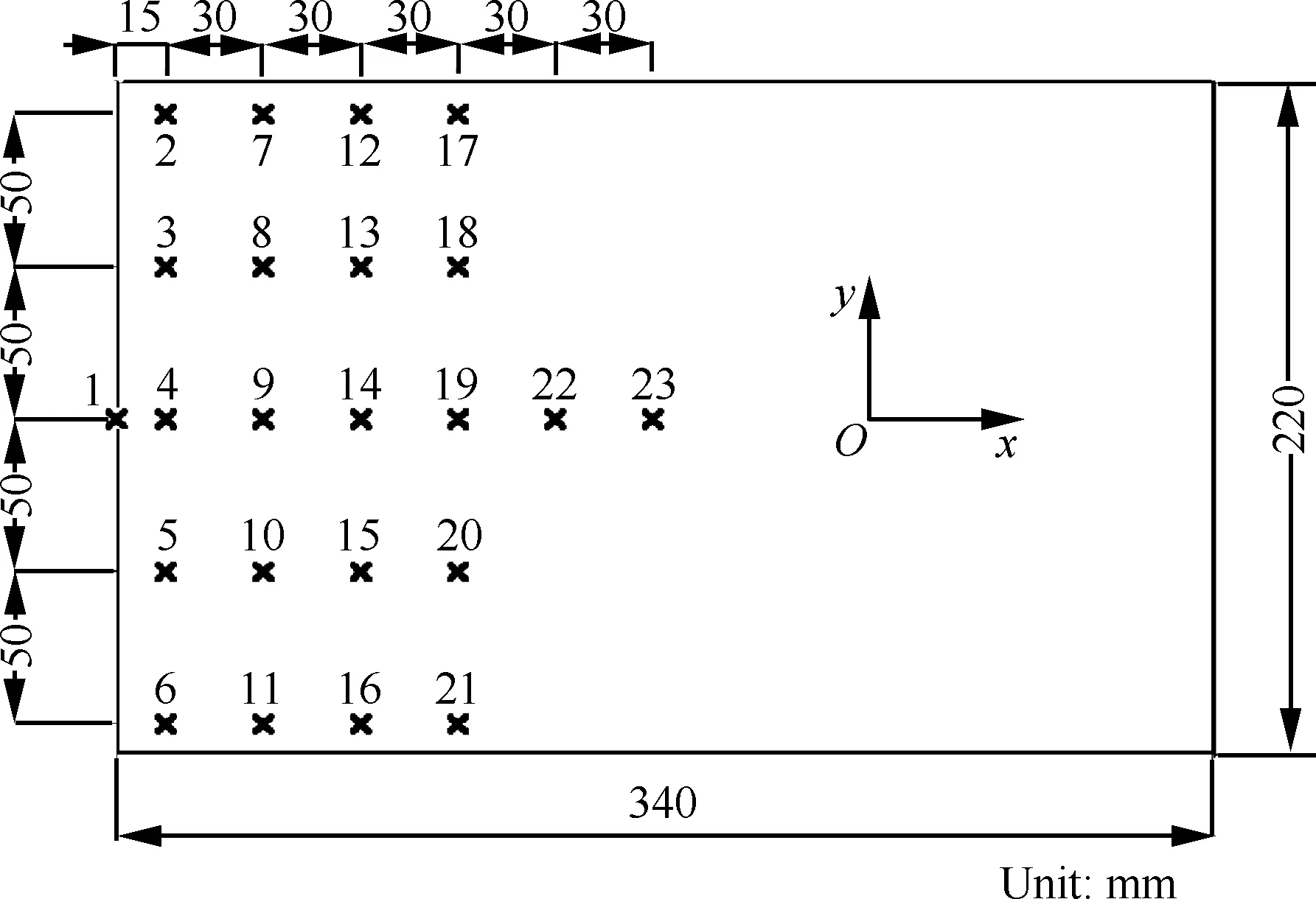
图14　矩形板上温度传感器的位置Fig.14　Temperature sensor locations on rectangular plate

表3给出了控温点(23号)为600 ℃时，矩形板中轴线上安装的7个温度传感器(1，4，9，14, 19，22，23)的测量数据。由表3中的数据可知, 控温点(23)达到目标温度600 ℃之后，根部1号传感器的温度只有182 ℃，从4号传感器至23号传感器止，两个测点之间的温度差别分别为35.2%、13.0%、8.2%、1.7%, 温度差逐渐减小，表明试验件根部与控温点之间的温度为非线性分布，远离根部后温度逐渐趋于一致。根据中心线处各传感器的实测温度值，使用最小二乘法进行数据拟合，可获得试验件中轴线上的根部与控温点之间的温度分布情况。

表3矩形板表面中轴线上各测点的温度值(控温点温度600 ℃)

Table 3Temperature data from measured points along central axis of rectangular plate surface (600 ℃ at control point)

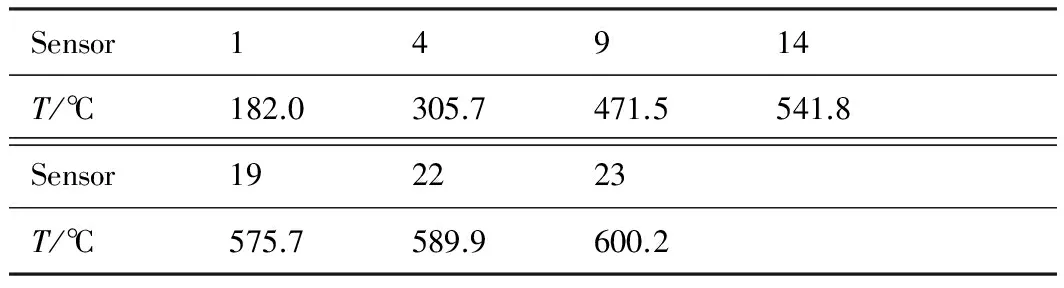
Sensor14914T/℃182．0305．7471．5541．8Sensor192223T/℃575．7589．9600．2

表4给出了图14中所示的矩形板表面5行4列交点处的实测温度值(控温点温度为600 ℃)。由表4中的数据可知，矩形板两个外边界处的温度要比中轴线x上的温度略低。从根部起，外边界的测点2、7、12、17的温度比中轴线上的4、9、14、19的温度分别低4.5%、2.7%、0.78%、0.25%，说明远离试验件根部后，边界温度和中轴线上的温度逐渐趋于一致。

图15给出了根据实测数据得到的矩形板上的温度分布示意图，由图15(a)中可以看到矩形板表面的全场温度分布概况，即试验件根部附近的温度变化比较大，远离根部后试验件温度逐渐趋于一致。从图15(b)中可看到试验件根部至控温点之间的温度梯度的变化。

表4矩形板表面5行4列交点处的温度值(控温点温度600 ℃)

Table 4Temperature data from measured points at intersections of 5 rows and 4 columns on rectangular plate surface (600 ℃ at control point)

SensorT/℃SensorT/℃SensorT/℃SensorT/℃2293．17458．712536．817567．83299．18465．813540．118568．14305．79471．514541．819575．75299．310464．515534．920569．16291．111461．116536．221567．3

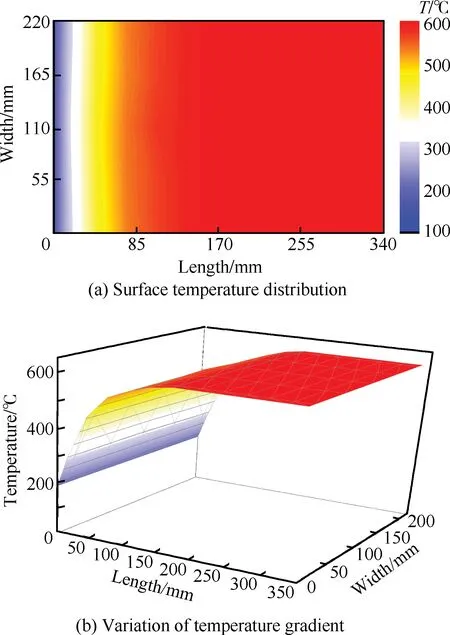
图15　矩形板上的温度场(控温点温度600 ℃)Fig.15　Temperature field on rectangular plate (600 ℃ at control point)

4　计算结果与试验结果的比较

图16为矩形板结构在20～1 100 ℃范围内的1～3阶模态频率的计算结果和试验结果对比图(1 800 s时)。由图中曲线可见，计算结果和试验结果的差别不大。表5为矩形板结构1～3阶模态频率的计算结果和试验结果(1 800 s时)。由表5中的试验数据可知，1 100 ℃的温度条件下，悬臂板1阶模态频率的试验值比常温时下降了12.1 Hz(25.5%)，2阶模态频率降低了40.4 Hz(24.6%)，3阶模态频率降低了62.1 Hz(21.1%)。

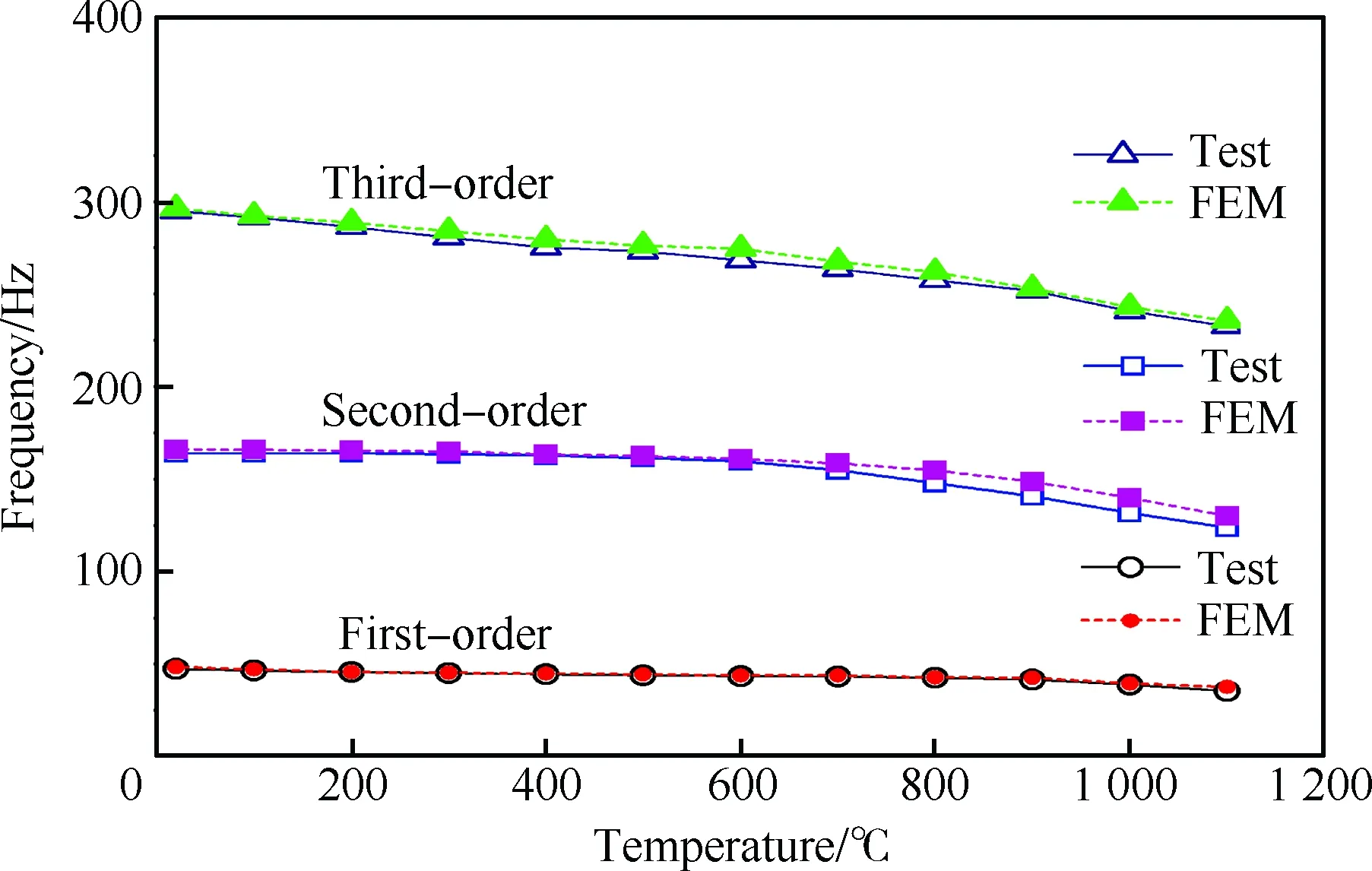
图16　矩形板不同温度下的模态频率变化(1 800 s时)Fig.16　Variation of modal frequencies for rectangular plate at various temperatures (at 1 800 s)

另外，由表5中可知，在20～1 100 ℃的温度范围内，矩形板结构前3阶模态频率的数值模拟结果和试验结果的相对误差均小于6.0%，说明数值计算与试验结果取得了比较良好的吻合性。

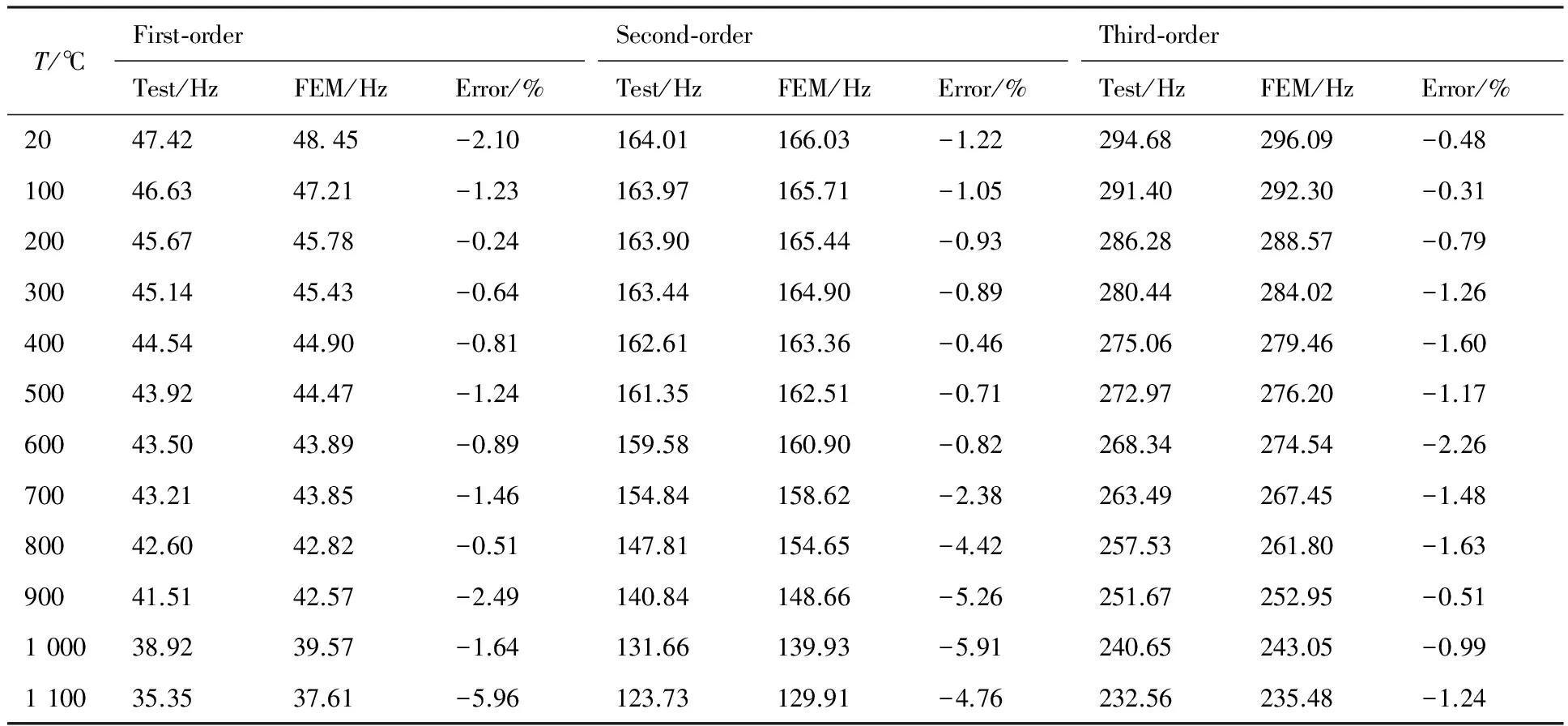
表5　矩形板结构1～3阶模态频率的试验值和数值计算结果(1 800 s时)

为了研究式(6)中不同因素对结构模态频率的影响，采用以下几种不同的计算方式：

1) 仅考虑材料随温度变化(K=KT，FEM-1)。

2) 材料随温度变化+热应力(K=KT+Kσ，FEM-2)。

3) 材料随温度变化+热变形(K=KT+KNL，FEM-3)。

4) 材料随温度变化+热应力+热变形(K=KT+Kσ+KNL，FEM-4)。

图17给出了条件1)～4)的计算结果。由图17 可知，本文模型中的热应力项Kσ及非线性项KNL均使各阶模态频率有一定程度的提高。虽然在温度较低时热应力项Kσ和非线性项KNL作用不明显，但是随着温度的升高，除去2阶模态频率之外，热应力项Kσ及非线性项KNL对1阶模态频率和3阶模态频率的影响呈现增加趋势，1 100 ℃时1阶模态频率的增加量超过10%。由此可知，针对本文中的悬臂板模型，当温度大范围变化时，在计算过程中需要考虑热应力和热变形对结构刚度及模态频率的影响。

图17　考虑不同因素的模态频率计算结果Fig.17　Numerical results of modal frequencies considering different factors

5　引伸杆附加质量的影响

由于加装引伸杆后的试验件的总质量会有所增加，加装引伸杆后的试验件的模态频率会比加速度传感器直接安装在试验件上所测得的模态频率稍低一点。为了尽量减少附加质量的影响，引伸杆的质量越小越好。本文中的陶瓷引伸杆的直径仅为4mm，且为中空结构，具有质量轻、耐高温(1 600 ℃)和刚性好的特点。本试验中矩形板结构试验件的质量为4 394g，单根引伸杆与紧固件的质量为34g，全部8根引伸杆和紧固件的总质量为272g。试验件与引伸杆件的质量比为16.2∶1，即引伸杆、紧固件等部件对翼面结构只增加了6.2%的附加质量，增重比不是很大。

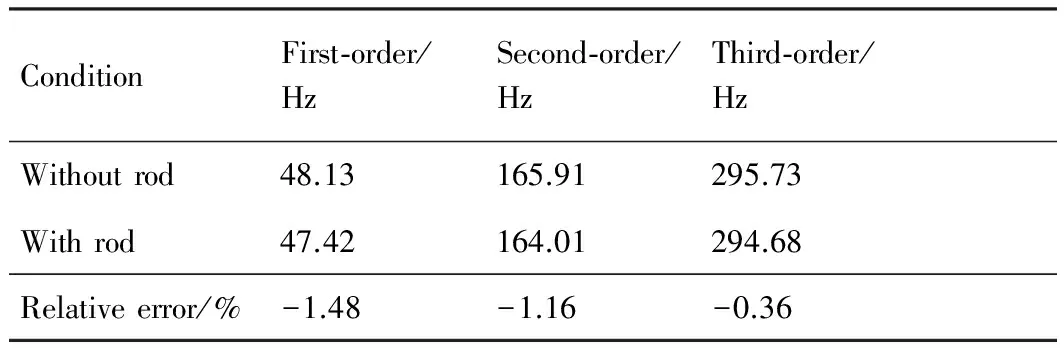
为了研究加装引伸杆后对试验件模态频率的影响，本文分别对无杆以及有杆状态下矩形板结构的模态频率进行了测量。表6给出了矩形板结构有杆和无杆时的前3阶模态频率的试验结果和相对误差。由表6的数据可知，加装引伸杆后测得的矩形板结构的模态频率要比将加速度传感器直接安装在试验件上所测得的模态频率有所下降。1阶模态频率约低1.48%，2阶模态频率低1.16%，3阶模态频率低0.36%，两者模态频率的差别均在2%以内，上述试验结果说明质量较轻的信号引伸装置对本试验件模态频率的影响不是十分显著，应该可以满足工程应用的要求，其试验结果也可对分析引伸杆附加质量的影响有一定的参考作用。

由于目前市售的高温加速度传感器的使用温度在650 ℃以下，并且高温环境下的测试结果还需要根据不同的温度区段进行非线性校正，其准确性也存在一定的问题。因此，目前还无法将市售的加速度传感器直接安装在高至1 200 ℃的试验件表面来完成振动信号的测量。虽然本文中的引伸杆附加质量影响的对比试验是在常温下进行的，若引伸杆在高温下的抗变形能力非常强，刚度足够大，则信号传递损失小，常温下实测得到的有杆和无杆方式的模态频率的对比数据，在一定程度可以作为高温时分析和修正附加质量影响的参考依据。

表6有杆和无杆时矩形板结构1～3阶模态频率(常温下)

Table 6First-, second- and third-order modal frequencies of rectangular plate structure with/without rod (at room temperature)

ConditionFirst⁃order/HzSecond⁃order/HzThird⁃order/HzWithoutrod48．13165．91295．73Withrod47．42164．01294．68Relativeerror/%-1．48-1．16-0．36

6　结　论

1) 由于远程高超声速飞行器翼、舵等板状结构会面临极为严酷的高温环境和长时间的剧烈振动，为了获得难于测量的恶劣高温环境下的结构振动特性参数，将瞬态气动热试验模拟系统与振动试验系统相结合，建立了高温热/振联合试验测试系统，实现了高达1 200 ℃高温环境下矩形板结构的热模态性能测试。

2) 试验结果表明，单边固支的矩形板结构的模态频率随着温度的提高呈现下降趋势，升温速率越大，模态频率的变化越快，且试验件表面温度越高，模态频率的下降幅度越大。在1 100 ℃高温环境下，本试验件1阶模态频率比常温时下降了25.5%，2阶模态频率下降了24.6%，3阶模态频率下降了21.1%。

3) 将试验结果和数值计算结果进行了对比验证。由对比结果可知，在20～1 100 ℃的温度范围内，矩形板结构前3阶模态频率的计算结果和试验测试结果的相对误差小于6.0%(绝大部分小于3.0%)，说明计算结果与试验结果具有比较良好的一致性，验证了试验方法的可信性及可用性。

4) 通过常温下有杆和无杆的对比试验可知，本试验中两种对比方式的模态频率的差别小于2%。说明使用质量轻的耐高温陶瓷引伸杆对矩形板结构模态频率的影响不是十分显著，所获得的对比数据可以作为分析和修正附加质量影响时的参考依据。为了减少引伸杆质量引起的测量误差，需要采用质量轻、耐高温和刚性好的引伸杆作为信号传递部件。

5) 本试验中1 200 ℃高温下单端固支矩形板结构的1阶模态频率相对于其他温度下的频率变化幅度，出现了很大的差别。这种当温度超过一定数值后，模态频率的变化出现明显异常的试验结果，对于确定该结构的安全使用极限具有重要参考价值。

6) 本研究结果为高超声速飞行器翼、舵及垂尾等板状结构在高温环境下的热模态分析以及安全可靠性设计提供了重要的试验手段。

[1]EARL T. Thermal structures for aerospace applications[M]. Reston: AIAA, 1996: 5-8.

[2]LEE I, LEE D M, OH L K. Supersonic flutter analysis of stiffened laminated plates subjected to thermal load[J]. Journal of Sound and Vibration, 1999, 234(1): 49-67.

[3]BROWN A M. Temperature-dependent modal test analysis correlation of X-34 FASTRAC composite rocket nozzle[J]. Journal of Propulsion and Power, 2002, 18(2): 284-288.

[4]CHAKRAVERTY S, PRADHAN K K. Free vibration of exponential functionally graded rectangular plates in thermal environment with general boundary conditions[J]. Aerospace Science and Technology, 2014, 36: 132-156.

[5]FAN Y, WANG H. Nonlinear vibration of matrix cracked laminated beams containing carbon nanotube reinforced composite layers in thermal environments[J]. Composite Structures, 2015, 124: 35-43.

[6]VOSTEEN L F, MCWITHEY R R, THOMSON R G. Effect of transient heating on vibration frequencies of some simple wing structures: NACA TN 4054[R]. Washington, D.C.: NACA, 1955.

[7]VOSTEEN L F, FULLER K E. Behavior of a cantilever plate under rapid-heating conditions: NACA RM L55E20[R]. Washington, D.C.: NACA, 1955.

[8]MCWITHEY R R, VOSTEEN L F. Effects of transient heating on the vibration frequencies of a prototype of the X-15 wing: NACA TN D-362[R]. Washington, D.C.: NACA, 1960.

[9]KEHOE M W, SNYDER H T. Thermoelastic vibration test techniques: NASA TM 101742[R]. Washington, D.C.: NASA, 1991.

[10]SNYDER H T, KEHOE M W. Determination of the effects of heating on modal characteristics of an aluminum plate with application to hypersonic vehicles: NASA TM 4274[R]. Washington, D.C.: NASA, 1991.

[11]NATALIE D S. High-temperature modal survey of a hot-structure control surface[C]//Proceedings of the 27th International Congress of the Aeronautical Sciences. Nice, France: French Society of Aeronautics and Astronautics, 2010, 3: 2091-2110.

[12]JEON B H, KANG H W, LEE Y S. Free vibration characteristics of rectangular plate under rapid thermal loading[C]//The 9th International Congress on Thermal Stresses. Budapest: Hungarian Academy of Sciences, 2011.

[13]CHENG H, LI H, ZHANG W, et al. Effects of radiation heating on modal characteristics of panel structures[J]. Journal of Spacecraft and Rockets, 2015, 52(4): 1228-1235.

[14]吴大方, 赵寿根, 潘兵, 等. 高速巡航导弹翼面结构热-振联合试验研究[J]. 航空学报, 2012, 33(9): 1633-1642.

WU D F, ZHAO S G, PAN B, et al. Research on thermal-vibration joint test for wing structure of high-speed cruise missile[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1633-1642 (in Chinese).

[15]刘浩, 李晓东, 杨文岐, 等. 高速飞行器翼面结构热振动试验的TARMA模型方法[J]. 航空学报, 2015, 36(7): 2225-2235.

LIU H, LI X D, YANG W Q, et al. Thermal vibration test on wing structure of high-speed flight vehicle using TARMA model method[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2225-2235 (in Chinese).

[16]YU K, YANG K, BAI Y. Experimental investigation on the time-varying modal parameters of a trapezoidal plate in temperature-varying environments by subspace tracking-based method[J]. Journal of Vibration and Control, 2015, 21(6): 3305-3319.

[17]吴大方, 赵寿根, 潘兵, 等. 高速飞行器中空翼结构高温热振动特性试验研究[J]. 力学学报, 2013, 45(4): 598-605.

WU D F, ZHAO S G, PAN B, et al. Experimental study on high temperature thermal-vibration characteristics for hollow wing structure of high-speed flight vehicles[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 598-605 (in Chinese).

[18]吴大方, 王岳武, 蒲颖, 等. 高超声速飞行器复合材料翼面结构1 100 ℃高温环境下的热模态试验[J]. 复合材料学报, 2015， 32(2): 323-331.

WU D F, WANG Y W, PU Y, et al. Thermal modal test of composite wing structure in high-temperature environments up to 1 100 ℃ for hypersonic flight vehicles[J]. Acta Materiae Compsitae Sinica, 2015, 32(2): 323-331 (in Chinese).

[19]WU D F, WU S, WANG Y W, et al. High-speed and accurate non-linear calibration of temperature sensors for transient aerodynamic heating experiments[J]. Transactions of the Institute of Measurement and Control, 2014, 36(6): 845-852.

[20]WU D F, WANG Y W, PAN B, et al. Experimental research on the ultimate strength of hard aluminum alloy 2017 subjected to short-time radioactive heating[J]. Materials & Design, 2012, 40: 502-509.

[21]ZHENG L M, WU D F, ZHOU A F, et al. Experimental and numerical study on heat transfer characteristics of metallic honeycomb core structure in transient thermal shock environments[J]. International Journal of Thermophysics, 2014, 35(8): 1557-1576.

[22]科恩L. 时-频分析: 理论与应用[M]. 白居宪, 译. 西安: 西安交通大学出版社, 1998: 77-93.

COHEN L. Time-frequency analysis: Theory and applications[M]. BAI J X, translated. Xi’an: Xi’an Jiaotong University Press, 1998: 77-93 (in Chinese).

[23]《中国航空材料手册》编辑委员会. 中国航空材料手册: 第1卷[M]. 2版. 北京: 中国标准出版社, 2002: 817-826.

The Editorial Board of China Aeronautical Material Handbook. China aeronautical material handbook: Vol.1[M]. 2nd ed. Beijing: Standard Press of China, 2002: 817-826 (in Chinese).

吴大方男， 博士， 教授， 博士生导师。主要研究方向： 高速飞行器结构热防护, 结构振动主动控制， 实验力学。

Tel: 010-82317507

E-mail: wdf1950@163.com

王岳武男， 博士研究生。主要研究方向： 实验力学。

Tel: 010-82317507

E-mail: wangyuewu@buaa.edu.cn

Test research and numerical simulation on thermal modal ofplate structure in 1 200 ℃ high-temperature environments

WU Dafang*, WANG Yuewu, SHANG Lan, PU Ying, WANG Huaitao

School of Aeronautic Science and Engineering, Beihang University, Beijing100083, China

When the hypersonic aircraft flies at a high Mach number, the plate-like attitude control structures, such as the wings and rudders, will be exposed to an extremely high-temperature environment. In this paper, in order to obtain the thermal modal parameters of structure that are difficult to measure, high-temperature transient heating test system and vibration test system are combined to establish a thermal/vibration test system and the experimental measurement for key vibration characteristic parameters of structure in a thermal-vibration coupled environment up to 1 200 ℃ (e.g. the modal frequency and modal vibration shape) is performed. Meanwhile, the numerical simulation on the thermal modal characteristics of rectangular plate is carried out and the test results are compared with the numerical results. In the test, a self-developed extension configuration of high-temperature-resistant ceramic pole is used to transfer the vibration signals of structure to nonhigh temperature zone, and the acceleration sensors are applied to identifying the vibration signals. Test data are analyzed by a time-frequency joint analysis technique. The tested modal frequencies of the plate in high temperature environments ranging from 200 ℃ to 1 100 ℃ coincide favorably with calculated results, which verifies the credibility and effectiveness of the proposed experimental methods. The research results can provide an important basis for the dynamic performance analysis and safety design of structure under high-temperature thermal-vibration conditions for hypersonic aircraft.

hypersonic aircraft; thermal modal test; numerical calculation; high-temperature environments; vibration characteristics

2015-11-17； Revised： 2015-12-23； Accepted： 2016-03-10； Published online： 2016-03-1712：57

National Natural Science Foundation of China (11427802)

. Tel.： 010-82317507E-mail: wdf1950@163.com

2015-11-17； 退修日期： 2015-12-23； 录用日期： 2016-03-10；

时间： 2016-03-1712:57

www.cnki.net/kcms/detail/11.1929.V.20160317.1257.006.html

国家自然科学基金 (11427802)

.Tel.： 010-82317507E-mail: wdf1950@163.com

10.7527/S1000-6893.2016.0075

V216.2； V216.4

A

1000-6893(2016)06-1861-15

引用格式： 吴大方， 王岳武， 商兰， 等．1 200 ℃高温环境下板结构热模态试验研究与数值模拟[J]． 航空学报, 2016, 37(6): 1861-1875. WU D F, WANG Y W, SHANG L, et al. Test research and numerical simulation on thermal modal of plate structure in 1 200 ℃ high-temperature environments[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1861-1875.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160317.1257.006.html