具备强表达能力的选择密文安全高效属性基加密方案

张 凯 魏立斐 李祥学 陈 洁 钱海峰

1(华东师范大学计算机科学技术系 上海 200241)2(综合业务网理论及关键技术国家重点实验室(西安电子科技大学) 西安 710071)3(上海海洋大学信息学院 上海 201306)4(卫士通摩石实验室 北京 100070) (zhangkaiecnu@163.com)



具备强表达能力的选择密文安全高效属性基加密方案

张 凯1,2魏立斐3李祥学1,4陈 洁1,2钱海峰1

1(华东师范大学计算机科学技术系 上海 200241)2(综合业务网理论及关键技术国家重点实验室(西安电子科技大学) 西安 710071)3(上海海洋大学信息学院 上海 201306)4(卫士通摩石实验室 北京 100070) (zhangkaiecnu@163.com)

属性基加密(attribute-based encryption, ABE)是一种新型公钥加密体制，它实现了对加密数据的细粒度访问控制.在密钥策略属性基加密方案(key-policy attribute-based encryption, KP-ABE)中，密文与属性集合相关联，密钥则与访问控制结构相关联.因此在大多数KP-ABE方案中，解密开销与解密算法所涉及的属性数目成正比.结合Hohenberger和Waters提出的快速解密属性基加密方案的思想，构造了一个同时支持非单调访问结构、大属性空间的选择属性集合和选择明文安全快速解密密钥策略属性基加密方案，并在随机预言机模型下证明是选择性属性集合和选择明文安全的；并在此基础上，利用Lai等人提出的合数阶上具有强表达能力的快速解密KP-ABE方案的思想，再结合用于给出构造选择密文安全的KP-ABE方案的变色龙Hash技术，构造了一个同样支持非单调的访问控制结构且表达能力丰富的选择密文安全快速解密KP-ABE方案.比较相关方案，所提出的2个方案都具备相当的解密效率.

属性基加密；选择密文安全；非单调访问结构；快速解密；大属性空间

随着云计算服务、大数据技术的普及，传统的公钥加密方案及身份基加密(identity-based encryp-tion, IBE)[1,2]不足以适应“一对多”的网络服务需求[3].作为一种新型的公钥加密体制，属性基加密(attribute-based encryption, ABE)[4,5,6]被认为是IBE体制的扩展概念，它能够保证数据发送方与数据接收方按照设定的访问策略共享数据，使用户能够更加安全、高效地享受新型网络服务[7].通常，ABE分为2种类型：密钥策略属性基加密(key-policy attribute-based encryption, KP-ABE)和密文策略属性基加密(ciphertext-policy attribute-based encryption, CP-ABE).在KP-ABE方案中，密文是与一组属性集合相关联，密钥则是与基于属性构成的访问结构相关联；而在CP-ABE方案中，密钥是与一组属性集合相关联，密文则是与基于属性构成访问结构相关联.

由于ABE具备细粒度的访问控制能力，这也给ABE方案带来较大的计算开销.在典型ABE中，解密开销常常与在解密过程中所需要用到的属性数目成正比，至少需要|Δ|个双线性对运算，其中|Δ|为解密过程中所需的属性数目.这大大限制ABE在资源受限环境(如弱密码设备)中的应用.基于此问题，Hohenberger和Waters提出了第1个快速解密ABE方案[8]，该方案是基于GPSW中的KP-ABE方案[4]，将原有密钥更加细化、增加更多的“帮助层”元素.在密钥生成算法时间和密钥长度略增的前提下，解密过程所需的双线性运算个数降为常数量级的2次运算，并给出2种变种方案.

在此之后，Lai等人[9]采用聚合技术实现了固定短密文长度性质，给出一个合数阶上的快速解密且表达能力丰富的KP-ABE方案，并利用双系统证明技术证明该方案在适应性安全模型下是安全的.不过该聚合技术只能应用到小属性空间KP-ABE方案的构造上.然而，对于小属性空间的ABE方案，通常要求系统建立算法需要事先确定属性的数目，这使得属性空间的大小往往与安全参数λ是多项式倍的关系.而在大属性空间[10]的方案，属性空间的大小往往不需要在系统建立算法中事先确定好，它与安全参数λ是指数倍的关系，具备更大的灵活度.

对于公钥加密方案，可抵抗选择密文攻击(chosen ciphertext attack, CCA)是比可抵抗选择明文攻击(chosen plaintext attack, CPA)更被广泛接受的一种语义安全性.具体到构造CCA安全的KP-ABE，最初是通过对Canetti-Halevi-Katz转换方法[11]稍加调整得到.之后，Yamada等人给出一种从CPA安全到CCA安全ABE方案的通用转换方法[12]，但要求ABE方案满足可代理性质或者可验证性质.不过，这些方案都需要使用一次签名.之后，有不使用一次签名而直接给出CCA安全的ABE构造[13-14]，不过这些方案仅能支持门限访问结构策略.最近，Liu等人[15]通过观察Boyen-Mei-Waters方法[16]，创新性地将在线离线签名的变色龙Hash技术[17]应用到加密方案中，最终给出一个选择密文安全KP-ABE方案的直接构造，但该方案要求ABE方案需支持大属性空间特性.

在ABE体制中，基于属性的访问结构有单调访问结构和非单调访问结构2种[18].具体来说，单调访问结构仅支持“与”、“或”、“门限”操作，而非单调访问结构可以额外支持“非”操作.因此，非单调的访问结构允许用户的私钥可以基于任意访问结构生成，加大了方案的表达能力，增加了ABE方案的具体实际应用场景的范围.

本文在已有工作的基础上，给出2个具体的支持快速解密性质的KP-ABE构造：

1) 观察文献[8]中的方案，利用实现非单调访问结构的技术[18-19]，借助随机预言机[20]使得方案支持大属性空间.最终提出一个支持非单调访问结构、支持大属性空间的快速解密素数阶KP-ABE构造，并证明是满足选择属性集合和选择明文安全性定义.

2) 基于方案1，借鉴实现支持任意单调访问结构技术[11]，将原有方案表达能力进一步加强.观察Liu等人[15]用于直接构造CCA安全KP-ABE方案的变色龙Hash技术[17].最终提出一个具备丰富表单能力、支持非单调访问结构、支持大属性空间的高效选择密文安全快速解密素数阶KP-ABE方案构造.

1 预备知识

1.1 访问结构

定义1. 令{P1,P2,…,Pn}是一个参与方集合.一个单调的访问结构是指一个非空的集合⊆2{P1,P2,…,Pn}{∅}：对于任意B,C，若B∈且B⊂C，则C∈.在的集合被称为授权集合，不在的集合被称为非授权集合.

1.2 线性秘密分享方案

令S∈是一个任意授权集合，I⊂{1,2,…,}定义为I⊂{i|ρ(i)∈S}.若{λi}是根据∏关于任意秘密s的有效分享碎片，则存在一组常数集合{μi}i∈I，满足μiλi=s.令Wi表示W中的第i行，有).其中{μi}i∈I可以通过高斯消除法计算得到.

1.3 密钥策略属性基加密

一个KP-ABE方案由4个算法构成：

1) 系统建立Setup(1λ).系统建立算法以安全参数λ作为输入；输出公开参数MPK以及主密钥MSK.

2) 加密Encrypt(MPK,M,S).加密算法以公开参数MPK、消息M和属性集合S作为输入；输出密文CT.

3) 密钥生成KeyGen(MPK,MSK,).密钥生成算法以MPK、MSK、访问结构作为输入；输出一个基于访问结构的密钥SK.

4) 解密Dec(MPK,CT,SK).解密算法输入公开参数MPK、密文CT以及密钥SK.当属性集合满足访问结构，即S∈时，算法返回消息M.

安全模型：KP-ABE的安全模型是由一个挑战者和一个攻击者A完成的游戏进行定义：

1) 系统建立阶段.挑战者运行Setup算法，并将公开参数MPK发送给攻击者.

2) 询问阶段1.该阶段攻击者将会自适应地向挑战者发出2种询问：

② 密文问询.攻击者问询关于集合S的密文CT.挑战者构造使得S能够满足的访问结构，运行密钥生成算法KeyGen(MPK,MSK,)得到密钥SK；再运行解密算法Dec(MPK,CT,SK)解密密文CT，并将得到的结果返回给攻击者.

3) 挑战阶段.攻击者递交2个等长的消息M0,M1.除此之外，还会递交一个属性集合S*，但该集合不能满足询问阶段的任一访问结构.挑战者随机掷一枚硬币b，然后基于属性集合S*加密Mb得到挑战密文CT*，并将CT*传递给攻击者.

4) 询问阶段2.与阶段1相同.

5) 猜测阶段.攻击者会输出关于b的猜测值b′.实验输出结果1当且仅当b=b′.

定义3. 对于所有的概率多项式时间攻击者A，如果存在一个可忽略函数使得

成立，对于属性空间U的密钥策略属性基加密方案KP-ABE是选择密文安全的.

选择性属性集合安全(selective security).如果在系统建立阶段之前增加一个初始化阶段，在该阶段中攻击者必须将要挑战的属性集合S*发送给挑战者，那么认为该KP-ABE方案是选择性属性集合安全.

选择明文安全(chosen plaintext security).如果在询问阶段中将密文问询阶段去除掉，那么认为该KP-ABE方案是选择明文安全的.

1.4 双线性映射

1) 双线性性.对于所有的u,v∈和a,b∈p，有e(ua,vb)=e(u,v)ab.

2) 非退化性.e(g,g)≠1.

定义4. 判定性BDHE.令a,s∈p是随机选取的元素，g是一个阶为p∈Θ(2λ)群的生成元.判定性q-BDHE是指给定向量：

y=(,p,g,gs,ga,…,g(aq),g(aq+2),…,g(a2q)),

对于所有的概率多项式时间攻击者A，以一个关于λ的可忽略优势区分e(g,g)aq+1s∈T和一个随机元素R∈T.攻击者A的优势定义如下：

|Pr[A(y,e(g,g)aq+1s)=0]-Pr[A(y,R)=0]|,

2 CPA安全的快速解密KP-ABE方案

基于文献[8]提出的快速解密KP-ABE方案，文献[19]给出一个支持属性变成函数加密[21]方案的KP-ABE方案，并实现了固定短密文长度.通过观察这2个KP-ABE方案[8,19]，借助随机预言机结合非单调访问结构技术，本节给出一个在选择性属性集合安全和选择明文安全模型下、支持非单调访问结构、大属性空间及快速解密等良好性质的KP-ABE方案(注意到在支持快速解密特性同时，试图在大属性空间下实现固定密文长度这一工作仍是目前的一个公开问题).同时，该方案对下一节构造实际高效的选择密文安全的KP-ABE(同时保持支持非单调访问结构、大属性空间、快速解密等良好特性)做好准备工作.

最终，本节提出了一个支持非单调访问结构、大属性空间的快速解密KP-ABE方案.

2.1 KP-ABE方案描述

本节提出的KP-ABE方案由4个算法组成：

1) 系统建立Setup(1λ).系统建立算法选择一个素数阶为p∈Θ(2λ)的双线性群，随机选取一个生成元g∈.然后，选取随机元素h0,u∈和α∈p.令Hash函数H:{0,1}*→，令H作为一个预言机.给定任意比特串zi∈U，其中i∈|k|，定义hi=H(zi).最后，设置方案公开参数MPK=(,p,g,h0,H,e(g,g)α)以及主私钥MSK=(PK,α).

2) 加密Encrypt(MPK,M,S=(x1,x2,…,xk)⊆{0,1}*).加密算法以公开参数MPK、消息M∈T和给定属性集合S=(x1,x2,…,xk)⊆U作为输入.算法随机选取s∈p，对于任意的属性xi∈{0,1}*，其中i∈|k|，令hi=H(xi).输出密文CT=(S,rch,C,C0,C1,C2,C3)，其中C=M.

3) 密钥生成KeyGen(MPK,MSK,).密钥生成算法以MSK、一个非单调的访问结构作为输入.给定一个对于属性集合S的非单调访问结构，存在一个对于属性集合的单调访问结构满足关系=NM().令=(W,ρ)，其中W是一个×m的矩阵，映射ρ:[]→n.利用Share算法计算秘密碎片{λi}i∈[].对于分享矩阵W的每一行Wi，随机选取ri∈p，然后:

① 当ρ(i)是一个正常属性时，计算:

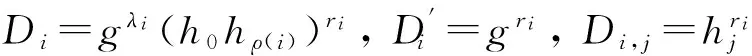
② 当ρ(i)是一个拒绝属性时，计算:

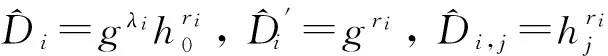
输出密钥：

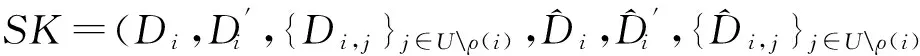
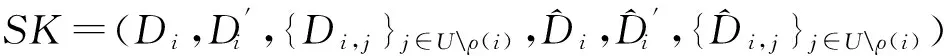
然后，对于每一行i，有：

① 当ρ(i)是一个正常属性时，解密可以先对密钥做预计算.计算：

再计算得到：

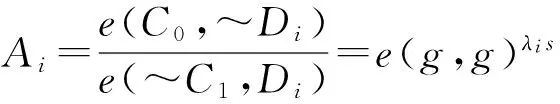
② 当ρ(i)是一个拒绝属性时，解密可以先对密钥做预计算.计算：

再计算得到：

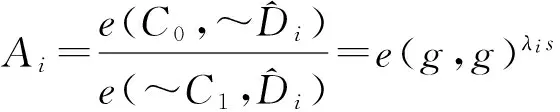
最后，解密算法可以计算得到:

3 安全性分析

结合文献[8,19]的证明技巧，特别是文献[19]的证明思路，本文采用定理1给出方案的安全性证明.

证明. 令e:×→T是一个双线性映射，|U|是属性集合中属性数目，这里|U|是关于安全参数1λ的多项式.假设存在一个PPT的攻击者，在实验中以不可忽略的概率输出结果1，那么就可以构造一个PPT的模拟器B打破群的|U|-BDHE问题，具体过程如下：

1) 初始化阶段.攻击者A提交用于生成挑战密文的属性集合S*.

2) 系统建立阶段.模拟器B收到来自|U|-BDHE关于系统参数的挑战输入：

(,p,g,gs,ga,…,ga|U|,ga|U|+2,…,ga2|U|,T),

其中，T=e(g,g)a|U|+1s或是T中的随机元素R.然后，随机选取α′∈p，设置e(g,g)α=e(g,g)α′·e(ga,ga|U|)，并私下设置α=α′+a|U|+1.最终，模拟器B将设置好的公开参数MPK发送给攻击者A.

3) 询问阶段1.模拟器B模拟预言机H:{0,1}*→如下：①在实验开始时初始化一个表TRO.②一旦收到关于属性xi的问询，模拟器B会首先检测该属性xi是否存在于表TRO中，若存在则直接返回结果；若不存在，则首先创建一个新表项(xi,i,hi)，并随机选取zi←p，计算hi=gzigai.这里，可以认为返回的结果hi是与中的随机元素独立同分布的.③再随机选取z0←p，并计算得到h0=gai.该阶段攻击者将会自适应地向挑战者发出密钥询问.攻击者问询关于非单调访问结构的密钥，挑战者会运行KeyGen算法将计算出的密钥返回给攻击者，分为2个步骤完成：

Ⅱ. 如果ρ(i)∉N(S*)，而且ρ(i)是一个正常属性时，则有ρ(i)∉S*.首先计算ci=v Wi，那么λi=αci=ci(α′+a|U|+1).利用消除技术去除密钥元素，令ri=-cia|U|+1-ρ(i)，因此模拟器B有能力计算：

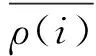
② 至此，模拟器B生成了有效密钥，但这些密钥并满足良好分布，需要再对这些密钥进行随机化操作，这里采用文献[9]中提到的技术.首先随机选取y2,y3,…,yn∈p，设置向量v#=(0,y2,y3,…,yn)，计算关于0的秘密分享碎片，得到i,j}j∈Uρ(i).之后，将第1步骤生成的有效密钥随机化:

*Di=Di(#Di),

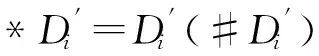
{*Di,j=Di,j(#Di,j)}j∈Uρ(i),

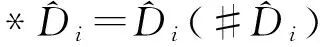
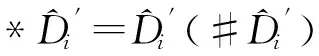
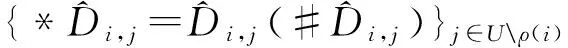
最终，将满足均匀随机分布的密钥传递给攻击者.

4) 挑战阶段.攻击者A提交2个等长的消息M0,M1,模拟器B会随机选取一个比特位b←{0,1}，然后基于挑战属性集合S*生成挑战密文:

C*=MT,

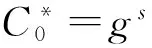
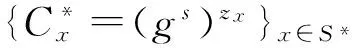
如果T=e(g,g)a|U|+1s，上面的密文是对Mb的有效加密，否则是对T中随机元素的加密.

5) 询问阶段2.与询问阶段1相同.

6) 猜测阶段.最终，攻击者输出一个关于的猜测值b′.如果b=b′，输出0(猜测T=e(g,g)a|U|+1s)；否则输出1(猜测T是一个随机值).

那么，B对A的回应是与KP-ABE的安全游戏同分布的.因此，当实验中A的输出为1,这则意味着B成功解决了判定性的|U|-BDHE问题.

证毕.

4 CCA安全的快速解密KP-ABE方案

Liu等人[15]利用变色龙Hash技术得到选择密文安全的KP-ABE的直接构造，使得在实现CCA安全性时带来很小的开销.本节试图利用该技术实现表达能力丰富的快速解密KP-ABE方案.但发现该技术只适用于大属性空间，因此借助随机预言机，将Lai等人提出的仅支持单调访问结构的小属性空间快速解密KP-ABE方案[9]拓展支持非单调访问结构大属性空间快速解密KP-ABE方案.基于第2节CPA安全性方案，最终提出CCA安全的KP-ABE方案.

Lai的方案能够支持任意单调访问结构，可以认为访问结构表达能力丰富.技术上是将属性空间分为2个部分：属性名和属性值.假设与密文绑定的属性集合数目恰好为n，而这n个属性又恰好来自于n个不同的属性名类.根据文献[9]有性质：对于每一个属性i分类的唯一属性zi，该属性集合可以被表示为(z1,z2,…,zn).对应一个访问结构(W,ρ,I)，其中W是一个×n的矩阵，映射ρ:[]→n,T=(tρ(1),tρ(2),…,tρ())∈，其中tρ(i)是访问结构下特定的属性名ρ(i).因此，一个属性集合S=(z1,z2,…,zn)满足访问结构(W,ρ,I)，当且仅当存在一个集合I⊆{1,2,…,}和一组常数{μi}i∈，对于所有i∈I满足关系：

在实现选择密文安全性时，借鉴变色龙Hash技术实现.本节寻找到一个基于decisional Diffie-Hellman的挑战密文结构g,gs′,uV,(uV)s′同样将对属性空间p分为2部分：1)用作正常属性空间U=；2)用作虚拟属性空间.这样就使得虚拟属性空间仅用作密文的有效性检测，并不能用来对正常属性空间的密文作检测.

最终，本节提出了一个具备丰富表达能力、支持非单调访问结构、大属性空间、选择密文安全快速解密KP-ABE方案.

4.1 方案描述

本节提出的KP-ABE方案由4个算法组成：

1) 系统建立Setup(1λ).系统建立算法选择一个素数阶为p∈Θ(2λ)的双线性群，随机选取一个生成元g∈.然后，选取随机h0,u∈和α∈p.这里，定义.因此，U∩V=∅,U∪V=p.令Hash函数H:U→，将令H作为一个预言机.给定任意zi∈U，其中i∈|k|，定义hi=H(zi).继而，定义一个变色龙Hash函数Hash:{0,1}*→V.最后，设定方案公开参数MPK=(Hash,,p,g,h0,H,u,ω,e(g,g)α)以及主私钥MSK=(PK,α).

2) 加密Encrypt(MPK,M,S=(z1,z2,…,zk)⊆U).加密算法以MPK、消息M∈T和给定属性集合S=(z1,z2,…,zk)⊆U作为输入.算法随机选取s,s′∈p，对任意的属性zi∈U，其中i∈|S|(定义|S|的值恰好是n)，令hi=H(zi).计算,随机选取rch←R并设置V=Hash(pkch,pkch‖C‖C0‖C1‖…‖Cn+1‖Cn+2,rch)∈V，再计算得到C4=(uV)s′ωs.输出密文CT=(S,rch,C,C0,{Ci}i∈[n]Cn+1,Cn+2,Cn+3)，其中:

C=Me(g,g)αs,

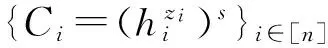
Cn+1=gs,

Cn+2=gs′,

Cn+3=(uV)s′ωs.

3) 密钥生成KeyGen(MPK,MSK,).密钥生成算法以MSK、一个非单调的访问结构作为输入.给定一个对于属性集合S的非单调访问结构，存在一个对于属性集合的单调访问结构满足关系=NM().令=(W,ρ)，其中W是一个×m的矩阵，映射ρ:[].令=(W,ρ,T)，其中W是一个×n的矩阵，映射ρ:[]→n，且T=(tρ(1),tρ(2),…,tρ())∈.该算法利用Share算法计算秘密碎片{λi}i∈[].对于分享矩阵W的每一行Wi，随机选取ri∈p，然后:

① 当ρ(i)是一个正常属性时，计算:

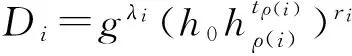
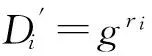
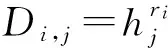
② 当ρ(i)是一个拒绝属性时，计算:

输出密钥:

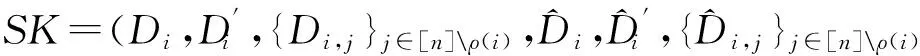
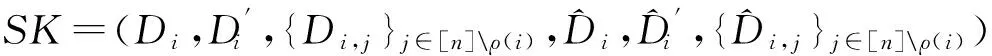
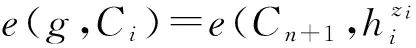
e(g,Cn+3)=e(Cn+2,uV)e(Cn+1,ω).

这里的密文有效性是可以公开检测的，因为所需要用到的公开参数MPK和密文都是公开的.

② 解密部分步骤.令(W,ρ,T)是对于的一个LSSS结构，可以找到一组I⊆{1,2,…,}和一组常数{μi}i∈，对于所有i∈I满足：

对在集合里面的密文元素做聚合操作，定义:

对于每一行i，有：

Ⅰ. 当ρ(i)是一个正常属性时，解密可以先对密钥做预计算.计算:

再计算得到:

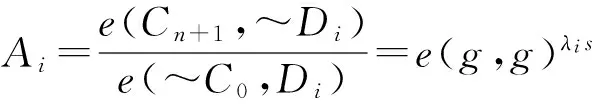
Ⅱ. 当ρ(i)是一个拒绝属性时，解密可以先对密钥做预计算.计算:

再计算得到:

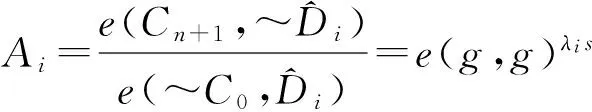
最后，解密算法可以计算得到:

4.2 安全性分析

在选择密文安全性的证明中，基本证明思路与第3节一致.但是，攻击者在阶段1和阶段2中除了自适应性地向攻击者问询关于访问结构的密钥外，同样可以发出密文问询.在这一部分的模拟中，与文献[12]中思路基本一致.

1) 当S⊄S*，得到问询密钥无法解密基于挑战属性集合生成的挑战密文；

2) 当S⊆S*和V≠V*，该部分满足正常属性空间构成的访问结构密钥，并不能解密关于基于虚拟属性空间生成的CCA的挑战密文结构；

3) 当S⊆S*和V=V*，模拟器无法模拟去回答，导致攻击者以1|V|=2(p-1)的概率使得游戏终止.

因此，最终在随机预言机模型下，可以证明在该方案基于|U|-BDHE和安全的变色龙Hash函数，本文的方案是选择性属性集合安全和选择密文安全的.

5 方案对比

本节将本文提出的2个快速解密KP-ABE方案与文献[8-9]进行对比，如表1所示:

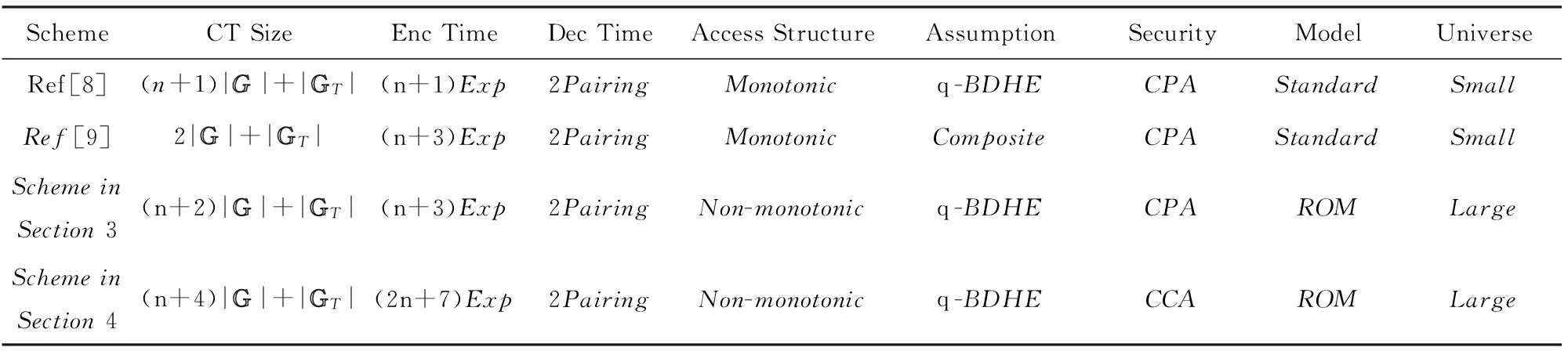
Table 1 Comparison with other KP-ABE schemes with Fast Decryption

本文第3节、第4节提出的方案均支持大属性空间、非单调访问结构.除此之外，第4节提出的快速解密KP-ABE方案额外支持了类似“属性复用”的功能以及选择密文安全性.在安全性假设方面，文献[11]的方案是依赖于合数阶群下的子群假设，而文献[9]和本文的方案则是依赖于素数阶群下的假设.对比其他相关工作，本文方案实现了一些良好性质，但却需要借助随机预言机实现.

表1在加密、解密时间的分析上，仅考虑“统治级”运算.其中，加密开销仅考虑群中幂运算(Exp)个数，解密开销仅考虑双线性对运算(Pairing)个数，可以看出4个方案解密开销相当.但是，本文的2个方案为了实现非单调访问结构，它们的密钥长度和解密开销中的幂次运算大约为文献[8-9]的2倍.特别地，为了在访问结构额外实现类似“属性复用”的功能，第4节的方案需要更多的加密开销.除此之外，由于本文的2个方案支持大属性空间，无法采用密文聚合技术，因此密文长度比文献[8]要分别多1个和3个群元素，而基于合数阶群假设的文献[9]则实现了固定密文长度.对比其他相关工作，本文虽然借助了随机预言机实现了一些良好性质，但却牺牲了一些空间和时间效率.

6 结束语

本文借助随机预言机安全给出2个支持非单调访问结构(表达能力丰富)、大属性空间的快速解密KP-ABE构造，其中1个实现选择明文安全性，1个实现选择密文安全性.本文的未来工作是在标准模型下得到适应性选择密文安全高效快速解密KP-ABE方案，并在大属性空间下实现短固定密文长度并支持非单调的访问控制结构.

[1]Dan B, Franklin M. Identity-based encryption from the weil pairing[J]. Siam Journal on Computing, 2003, 32(3): 213-229

[2]Shamir A. Identity-based cryptosystems and signature schemes[G] //LNCS196: Proc of Advances in Cryptography (CRYPTO 1984). Berlin: Springer, 1985, 21(2): 47-53

[3]Cao Z. New Directions of Modern Cryptography[M]. Boca Raton, Florida: CRC Press, 2012

[4]Goyal V, Pandey O, Sahai A, et al. Attribute-based encryption for fine-grained access control of encrypted data[G] //Proc of the 13th ACM Conf on Computer and Communications Security (CCS). New York: ACM, 2006: 89-98

[5]Sahai A, Waters B. Fuzzy identity-based encryption[G] //LNCS 3494: Proc of the 24th Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT). Berlin: Springer, 2005: 457-473

[6]Su Jinshu, Cao Dan, Wang Xiaofeng, et al. Attribute based encryption schemes[J]. Journal of Software, 2011, 22(6): 1299-1315(苏金树, 曹丹, 王小峰, 等. 属性基加密机制[J]. 软件学报, 2011, 22(6): 1299-1315)

[7]Fu Yingxun, Luo Shengmei, Shu Jiwu. Survey of secure cloud storage system and key technologies[J]. Journal of Computer Research and Development, 2013, 50(1): 136-145(傅颖勋, 罗圣美, 舒继武. 安全云存储系统与关键技术综述[J]. 计算机研究与发展, 2013, 50(1): 136-145)

[8]Hohenberger S, Waters B. Attribute-based encryption with fast decryption[G] //LNCS 7778: Proc of the 16th Int Conf on Practice and Theory in Public-Key Cryptography (PKC). Berlin: Springer, 2013: 162-179

[9]Lai J, Deng R H, Li Y, et al. Fully secure key-policy attribute-based encryption with constant-size ciphertexts and fast decryption[G] //Proc of the 9th ACM Symp on Information, Computer and Communications Security. New York: ACM, 2014: 239-248

[10]Yannis R, Waters B. Practical constructions and new proof methods for large universe attribute-based encryption[C] //Proc of the 2013 ACM SIGSAC Conf on Computer & Communications Security. New York: ACM, 2013: 463-474

[11]Ran C, Halevi S, Katz J. Chosen-ciphertext security from identity-based encryption[J]. SIAM Journal on Computing, 2007, 36(5): 1301-1328

[12]Yamada S, Attrapadung N, Hanaoka G, et al. Generic constructions for chosen-ciphertext secure attribute based encryption[G] //LNCS 6571: Proc of the 14th Int Conf on Practice and Theory in Public Key Cryptography (PKC). Berlin: Springer, 2011: 71-89

[13]Chen C, Zhang Z, Feng D. Efficient ciphertext policy attribute-based encryption with constant-size ciphertext and constant computation-cost[G] //LNCS 7778: Proc of the 5th Int Conf on Provable Security. Berlin: Springer, 2011: 84-101

[14]Ge A, Zhang R, Chen C, et al. Threshold ciphertext policy attribute-based encryption with constant size ciphertexts[G] //LNCS 7372: Information Security and Privacy. Berlin: Springer, 2012: 336-349

[15]Liu W, Liu J, Wu Q, et al. Practical direct chosen ciphertext secure key-policy attribute-based encryption with public ciphertext test[G] //LNCS 8713: Proc of the 19th European Symp on Research in Computer Security (ESORICS). Berlin: Springer, 2014: 91-108

[16]Xavier B, Mei Qixiang, Waters B. Direct chosen ciphertext security from identity-based techniques[G] //Proc of the 12th ACM Conf on Computer and Communications Security. New York: ACM, 2005: 320-329

[17]Krawczyk H M, Rabin T D. Chameleon hashing and signatures[EB/OL]. International Association for Cryptologic Research (1998-03-17) [2016-08-15]. http://eprint.iacr.org/1998/010

[18]Rafail O, Sahai A, Waters B. Attribute-based encryption with non-monotonic access structures[G] //Proc of the 14th ACM Conf on Computer and Communications Security (CCS). New York: ACM, 2007: 195-203

[19]Huo W, Pei J, Zhang K, et al. KP-ABE with attribute extension: Towards functional encryption schemes integration[G] //Proc of the 6th Int Symp on Parallel Architectures, Algorithms and Programming. Piscataway, NJ: IEEE, 2014: 230-237

[20]Bellare M. Random oracles are practical: A paradigm for designing efficient protocols[C] //Proc of the 1st ACM Conf on Computer & Communication Security. New York: ACM, 1970: 62-73

[21]Dan B, Sahai A, Waters B. Functional encryption: Definitions and challenges[G] //LNCS 6597: Proc of the 8th Theory of Cryptography Conf. Berlin: Springer, 2010: 253-273

Zhang Kai, born in 1990. PhD candidate. His main research interests include public key cryptography and information security.

Wei Lifei, born in 1982. PhD. His main research interests include cryptography and cyber security (Lfwei@shou.edu.cn).

Li Xiangxue, born in 1974. Professor and PhD supervisor. His main research interests include cryptography and information security (xxli@cs.ecnu.edu.cn).

Chen Jie, born in 1985. Professor and PhD supervisor. His main research interests include public key cryptography and information security (jchen@cs.ecnu.edu.cn).

Qian Haifeng, born in 1977. Professor and PhD supervisor. His main research interests include cryptography and network security.

An Efficient and Expressive Attribute-Based Encryption Scheme with Chose Ciphertext Security

Zhang Kai1,2, Wei Lifei3, Li Xiangxue1,4, Chen Jie1,2, and Qian Haifeng1

1(DepartmentofComputerScience&Technology,EastChinaNormalUniversity,Shanghai200241)2(TheStateKeyLaboratoryofIntegratedServicesNetworks(XidianUniversity),Xi’an710071)3(CollegeofInformationTechnology,ShanghaiOceanUniversity,Shanghai201306)4(WestoneCryptologicResearchCenter,Beijing100070)

Attribute-based encryption (ABE) is a promising version of public key encryption, since it enables fine-grained access control on the encrypted data. In a key-policy ABE (KP-ABE) scheme, every ciphertext is related to attributes set and each secret key is associated with an access structure. Therefore, the decryption overhead is usually proportional to the number of attributes used in decryption process in most existing KP-ABE schemes. Inspired by Hohenberger and Waters’ KP-ABE scheme with fast decryption, we propose a large universe KP-ABE with fast decryption supporting non-monotonic access structure, which is proven selective chosen attribute set secure and chosen plaintext secure in the random oracle model. Moreover, observing Lai et.al expressive KP-ABE with fast decryption and applying with Chameleon Hash technique used to give a direct chosen ciphertext secure KP-ABE construction, we also give a direct chosen plaintext secure KP-ABE construction in the random oracle model, which still achieves the following features: non-monotonic access structure, large-universe and fast decryption. Compared with the related work, both two expressive large universe KP-ABE schemes enjoy comparable time efficiency in decryption process.

attribute-based encryption (ABE); chosen ciphertext security; non-monotonic access structure; fast decryption; large-universe

2016-06-15；

2016-08-17

国家自然科学基金项目(61571191,61572192,61472142,61402282);上海市科学技术委员会科技项目(13JC1403502);上海市青年科技英才扬帆计划项目(14YF1404200,14YF1410400);综合业务网理论及关键技术国家重点实验室开放基金项目(ISN17-11);华东师范大学研究生科研创新实践资助项目

钱海峰(hfqian@cs.ecnu.edu.cn)

TP309

This work was supported by the National Natural Science Foundation of China (61571191, 61572192, 61472142, 61402282), the Project of Science and Technology Commission of Shanghai Municipality(13JC1403502), the Shanghai Yang-Fan Plan (14YF1404200, 14YF1410400), the Open Foundation of the State Key Laboratory of Integrated Services Networks (ISN17-11), and the East China Normal University Fund for Graduate Student's Scientific Research, Innovation and Practice.